微格课程成绩评定与模糊关系方程的解

李世菊, 张 倩

(1.四川师范大学 美术学院,成都 610066; 2.四川师范大学 数学与软件科学学院,成都 610066)

微格课程成绩评定与模糊关系方程的解

李世菊1, 张 倩2

(1.四川师范大学 美术学院,成都 610066; 2.四川师范大学 数学与软件科学学院,成都 610066)

首先定义了模糊关系方程的ε极小解,然后给出了利用模糊神经网络寻找max-min合成有限模糊关系方程的一个ε极小解的算法,证明了算法的收敛性。最后把模糊关系方程的解应用于大学微格课程成绩的评定,并用算例进行了说明。

模糊关系方程;模糊神经网络;ε极小解;算法;微格课程;成绩评定

大学微格课程成绩的公允影响着我们对师范类学生的正确培养方向,可以说是关乎师范类学生的合格培养。为此,笔者[1]提出微格课程成绩评定的数学模型。该模型最后归结为模型B=W∘A。其中:A=(aij)n×m为评价矩阵;B=(b1,b2, …,bm)为评价结果;W={w1,w2, …,wn}是由专家组对各评价因素集中每个因素按其对教学评价的重要程度给分所得。显然,W的合理性关乎整个模型的成败。由于W是专家组给出，难免受个人主观因素的影响而发生偏离实际的现象。我们的问题是如何纠正其中的主观因素。这实际上就是已知评价矩阵A和评价结果,问评价因素集W是否合理?这就归为模糊关系方程的求解问题。模糊关系方程是1976年法国学者E.Sanchez[2]最早开始研究,其核心就是在方程有解时找到所有解。1984年,研究者们证明了定义在[0,1]格上的max-min合成有限模糊关系方程在有解时,方程的解集可由方程的最大解和有限个极小解完全确定[3-4]。至此,对定义在[0, 1]格上max-min合成有限模糊关系方程的研究主要集中于寻找有效的方法去计算有限个极小解[5-6]。然而,2002年L.Chen等[7]证明了计算模糊关系方程的所有极小解是一个NPH问题。为此,人们尝试把模糊集与神经网络相结合,开始了用模糊神经网络求解模糊关系方程的研究,如李艳平等[8]就给出了基于模糊神经网络求解模糊关系方程的方法。1997年,Li Xiaozhong等[9]利用模糊神经网络在模糊δ规则的基础上提出了求解模糊关系方程最大解的算法。2002年,王加银等[10]改进了文献[9]中的算法。2012年，冯霜等[11]根据文献[9]又提出了基于模糊神经网络求模糊关系方程的极小解算法。本文将举例说明文献[11]中的算法是有缺陷的,并重新设计模糊神经网络,研究用模糊神经网络求解模糊关系方程一个ε极小解的方法,最后把模糊关系方程的解应用于大学微格课程成绩的评定,并用算例进行了说明。

1 问题的产生

本文以下的神经网络不同于一般的人工神经网络,而是模糊神经网络[12]。模糊神经网络的主要特点在于,不管是输入和输出信息还是神经元间的联接权值,都在[0, 1]中取值;而且,神经元的算子是形如式(1)的(∨,∧)算子,即取大取小算子

(1)

众所周知,误差反向传播算法(Back Propagation算法,简称为BP算法)是人工神经网络中常用的学习算法之一。然而,因为模糊神经网络中的算子(∨,∧)不可导,所以不能直接将BP算法应用于模糊神经网络。1997年,Li Xiaozhong等[9]利用模糊神经网络在模糊δ规则的基础上提出了求解模糊关系方程最大解的算法。2002年,王加银等[10]举例说明文献[9]中的算法是依赖于方程的排列顺序,为此他们改进了文献[9]中的算法。2012年,冯霜等[11]根据文献[9]给出了基于模糊神经网络求模糊关系方程的极小解算法。他们的训练算法Ⅰ与文献[9]中算法一样也是有缺陷的。以下我们先给出模糊关系方程极小解的定义,再以文献[11]中的例1来说明问题。

设A=(aij)m×n,B=(b1,b2, …,bm)T,称

A∘X=B

(2)

或任意i∈{1, 2, …,m},

为定义在[0,1]的模糊关系方程。其中:T表示转置;aij与bi∈[0,1]为已知;X=(x1,x2, …,xn)T为未知。记X={X|A∘X=B}。由文献[2]知下面引理成立。

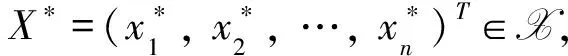
定义1[13]称X的极小元(如果存在)为模糊关系方程(2)的极小解。

例1[11]设模糊关系方程为A∘W=B。其中

易知方程最大解为Wmax=(0.2, 1.0, 0.4)T。用文献[11]的训练算法Ⅰ,取η=0.5,ε=0.000 01,可得到一个极小解为Wmin=(0.199 993 896, 0, 0.399 993 896)T[原文中Wmin=(0.2, 0, 0.4)T]。

若互换方程A∘W=B第二行与第三行,即

易知方程最大解仍为Wmax=(0.2, 1.0, 0.4)T。用文献[11]的训练算法Ⅰ,取η=0.5,ε=0.000 01,可得到Wmin=(0.199 993 896, 0.199 993 896, 0)T,但易验证这并不是方程的极小解。

上面例1说明文献[11]的训练算法Ⅰ的运行结果随方程的排列顺序改变而改变,且运行结果不一定是方程的极小解。不仅如此,我们还认为,用模糊神经网络不能求得精确的极小解Wmin=(0.2, 0, 0.4)T,一般仅能找到方程有一定误差的极小解,即我们将定义的ε极小解。

2 模糊神经网络的拓扑结构及求模糊关系方程ε极小解的算法

定义2设X0=(x10,x20, …,xn0)T是模糊关系方程(2)的极小解,ε为任意小的正数,如果X=(x1,x2, …,xn)T满足|x1-x10|2+|x2-x20|2+…+|xn-xn0|2<ε,则称X为方程(2)的ε极小解。

我们以下仅研究寻找max-min合成有限模糊关系方程(2)的一个ε极小解的算法。

我们选择的模糊神经网络为2层网络:第一层为输入层,由n个取小模糊神经元构成;第二层为输出层,由一个取大模糊神经元构成(图1)。用X=(x1,x2, …,xn)T为所示模糊神经网络的联接权向量,将模糊关系方程的已知信息转化为模糊神经网络的训练样本,用(ai1,ai2, …,ain)为网络的输入向量,bi为网络的输出预期值。这样,求解模糊关系方程(2)相当于寻求能存储训练样本集{(ai1,ai2, …,ain,bi)|1≤i≤m}的权向量X=(x1,x2, …,xn)T。

图1 模糊关系方程的神经网络Fig.1 The neural network of a fuzzy relational equation

本节给出求方程(2)的一个ε极小解的算法及算法的流程图(图2)。

算法1(求模糊关系方程ε极小解的网络训练算法)设方程A∘X=B的最大解X=(x1,x2, …,xn)T,ε为给定的任意小正数,η∈(0, 1]为学习效率,训练样本集为{(ai1,ai2, …,ain,bi)|1≤i≤m};

第一步j:=1;

第二步 把X中的第j个元素用0替换,即xj:=0,其余分量不变;

第三步i:=1,ei=0;

第四步 输入(ai1,ai2, …,ain,bi);

第六步 如果i=m,则转至第八步;

第七步i:=i+1,转至第四步;

第八步 如果ei≥ε,则转至第十二步;

第九步xj(t+1)=xj(t);

第十步 如果j=n,则转至第十三步;

第十一步j:=j+1,并转至第二步;

第十二步xj(t+1)=xj(t)+ηei,并转至第三步;

第十三步 输出X。

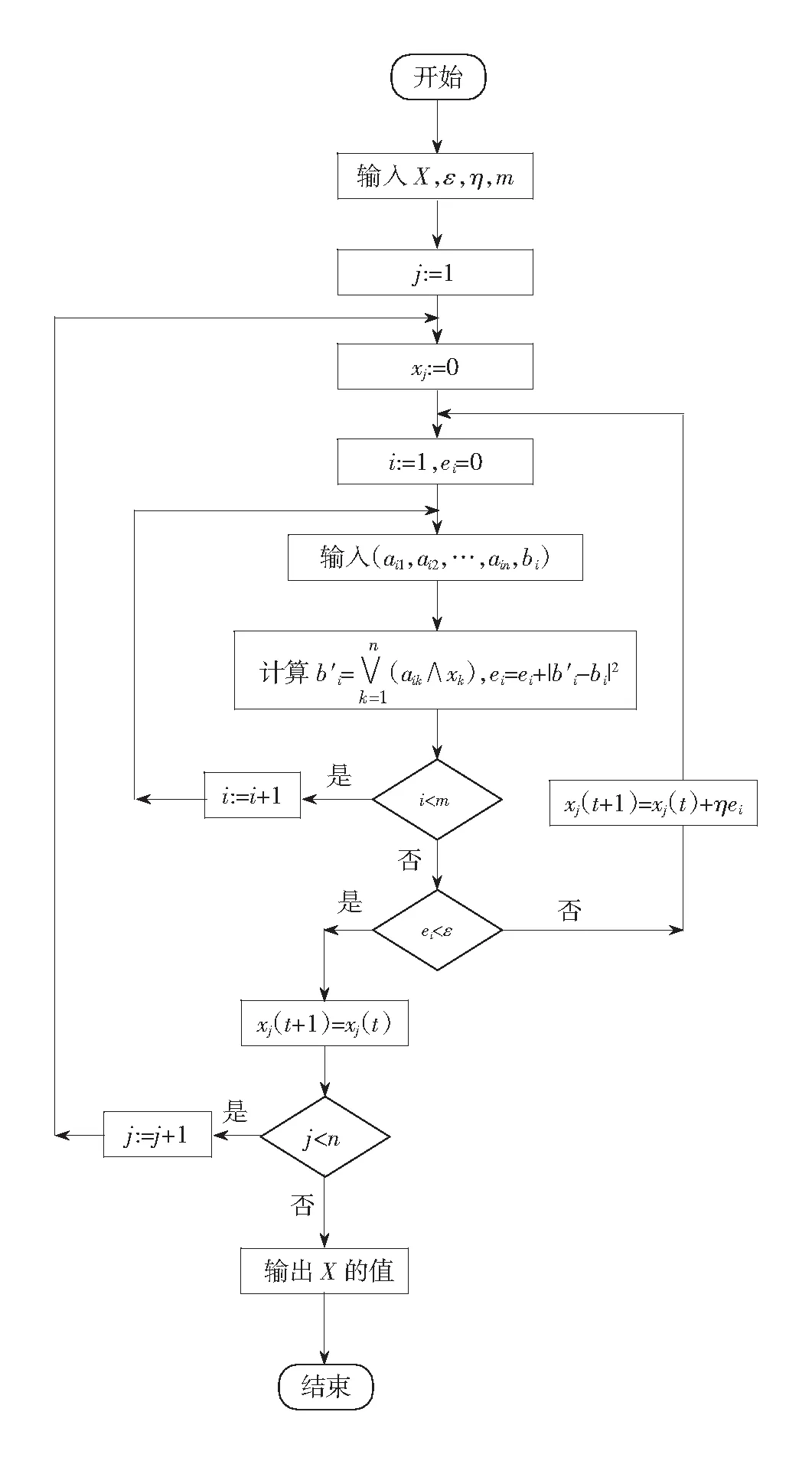
图2 算法1的流程图Fig.2 Flowchart of algorithm 1

定理1如果X(t)=(x1(t),x2(t), …,xn(t))T是由算法1产生的权值数列,那么它是单调递增数列。

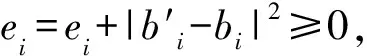
定理2算法1是收敛的。

证明只需证明算法1所得的权值数列X(t)=(x1(t),x2(t), …,xn(t))T收敛即可。根据定理1,X(t)=(x1(t),x2(t), …,xn(t))T中任意xj(t),j∈{1, 2, …,n},是单调递增数列,同时也是有界的,因为由算法1可知

O≤X(t)≤I。

其中:O是所有元素全为0构成的向量;I是所有元素全为1构成的向量。又由数学分析知单调有界数列xj(t),j∈{1, 2, …,n},收敛,定理2得证。

设

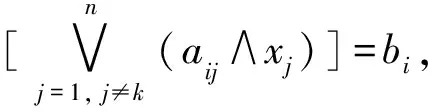
则下面命题成立。

命题1[13]X=(x1,x2, …,xn)T是方程(2)的极小解当且仅当任意k∈{1, 2, …,n},xk=min{a:a∈H(X,k)}。

定理3如果X≠∅,则算法1收敛到方程(2)的一个ε极小解。

证明由命题1,定义2及定理2即知。

3 应用于微格课程评定的算例

本节以我们在文献[1]中的例子为算例说明如何把模糊关系方程的ε极小解应用于微格课程成绩的评定。

例2设某高校5位微格教师在学生甲讲课后按评价因素w1“讲解”、w2“语言”、w3“板书”及w4“教态”给分情况统计得评价矩阵如下

大家公认学生甲的“讲解”得分0.4,“语言”得分0.5,“板书”得分0.2,“教态”得分0.1,即B=(0.4, 0.5, 0.2, 0.1)。而5位微格教师按评价因素(讲解、语言、板书及教态)的重要性给分统计情况为W=(0.5, 0.2, 0.2, 0.1),问所得W合理吗?

易知方程A∘X=B的最大解为X*=(1, 0.4, 0.2, 0.1)T。

取ε=0.000 01,学习效率η=1,从X的第一个分量开始替换,根据算法1能得到方程A∘X=B的ε极小解为X(1,2,3,4)=(0.390 147 899, 0, 0.190 645 432, 0)T,t=190。其中:X(1,2,3,4)表示替换顺序分别是第一个、第二个、第三个、第四个。根据算法1,计算知方程仅有ε极小解X0=(0.390 147 899, 0, 0.190 645 432, 0)T。

由引言部分分析知,评价因素向量W应该为方程A∘X=B的一个解。又由于X0≤W≤X*,因此,本例中5位微格教师给出的评价因素向量W是合理的。

4 结论

在应用算法1寻找方程(2)的ε极小解时，应注意下面3点：

a.算法1是从方程(2)最大解X*的第一个分量,顺序用0开始进行替换的。显然,我们也可从其余任何分量开始替换。

b.算法1收敛到{X(t)}的速度依赖于学习效率η的值。一般说来，η的值越大,xj(t)增加的速度越快,收敛到{X(t)}的速度也越快,训练所需的迭代次数和时间就越少。显然,精度ε取的值越大,利用算法1收敛到ε极小解的速度就越快。

c.改变模糊关系方程(2)的方程排列顺序,算法1的收敛结果{X(t)}不变。

作者感谢王学平教授的悉心指导及对本文的修改。

[1] 李世菊.微格课成绩评定的数学模型[J].模糊系统与数学,2017，31(1)：187-190. Li S J. The mathematical model for evaluating the student’s mark of a micro-class[J]. Fuzzy Systems and Mathematics, 2017, 31(1): 187-190. (in Chinese)

[2] Sanchez E. Resolution of composite fuzzy relation equations[J]. Information and Control, 1976, 30: 38-48.

[3] Czogala E, Drewniak J, Pedrycz W. Fuzzy relation equations on a finite set[J]. Fuzzy Sets and Systems, 1982, 7: 89-101.

[4] Higashi M, Klir G J. Resolution of finite fuzzy relation equations[J]. Fuzzy Sets and Systems, 1984, 13: 65-82.

[5] 汪培庄,罗承忠.有限Fuzzy关系方程极小解的个数[J].模糊数学,1984(3):63-70. Wang P Z, Luo C Z. The numbers of minimal solutions for a finite fuzzy relational equation[J]. Fuzzy Mathematics, 1984(3): 63-70. (in Chinese)

[6] 王学平.格[0,1]上求解Fuzzy关系方程的一种方法[J].高校应用数学学报:A辑,2000,15(2):127-133. Wang X P. A method to solve a fuzzy relational equation in a lattice [0, 1][J]. Appl Math J Chinese Univ: Ser A, 2000, 15(2): 127-133. (in Chinese)

[7] Chen L, Wang P P. Fuzzy relation equations (I): the general and specialized solving algorithms[J]. Soft Computing, 2002, 6: 428-435.

[8] 李艳平,李洪兴.基于神经网络的模糊关系方程解法[J].北京师范大学学报(自然科学版),1998,34(2):168-173. Li Y P, Li H X. Solution of fuzzy relation equation based on neural networks[J]. Journal of Beijing Normal University (Natural Science), 1998, 34(2): 168-173. (in Chinese)

[9] Li X Z, Ruan D. Novel neural algorithms based on fuzzyδrules for solving fuzzy relation equations: Part Ⅰ[J]. Fuzzy Sets and Systems, 1997, 90: 11-23.

[10] 王加银,李洪兴.基于模糊δ规则的模糊关系方程求解算法的改进[J].北京师范大学学报(自然科学版),2002,38(3):301-309. Wang J Y, Li H X. Modification of “Algorithm based on fuzzyδrules for solving fuzzy relation equations”[J]. Journal of Beijing Normal University (Natural Science), 2002, 38(3): 301-309. (in Chinese)

[11] 冯霜,李金权,温永川.基于神经网络的模糊关系方程极小解求解算法[J].北京师范大学学报(自然科学版),2012,48(2):111-114. Feng S, Li J Q, Wen Y C. A novel algorithm for obtaining minimal solutions of fuzzy relation equations based on neural networks[J]. Journal of Beijing Normal University (Natural Science), 2012, 48(2): 111-114. (in Chinese)

[12] Kosko B. Neural Networks and Fuzzy Systems[M]. New Jersey: Prentice-Hall, Englewood Cliffs, 1990.

[13] Di Nola A, Sessa S, Pedrycz W,etal. Fuzzy Relation Equations and Their Applications to Knowledge Engineering[M]. Boston: Kluwer Academic Publishers, 1989.

Thestudentsgradeevaluationofmicro-classandthesolutionofafuzzyrelationalequation

LI Shiju1, ZHANG Qian2

1.Collegeoffinearts,SichuanNormalUniversity,Chengdu610066,China; 2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,China

A method of student grade evaluation of micro-class is introduced in this paper. Firstly, theε-minimal solution of a fuzzy relational equation is defined. Secondly, an algorithm is introduced in order to find oneε-minimal solution from the fuzzy relational equation by using fuzzy neural network and then to determine its convergence. Finally, the solution of fuzzy relational equation is applied to the student grade evaluation and a numerical example is illustrated.

fuzzy relational equation; fuzzy neural network;ε-minimal solution; algorithm; micro-class; evaluation of the student’s mark

O159 [

] A

10.3969/j.issn.1671-9727.2017.05.13

1671-9727(2017)05-0631-05

2017-03-04。

国家自然科学基金项目(11171242)。

李世菊(1967-),女,硕士,讲师,研究方向:美术教育及微格教育教学等, E-mail:784760668@qq.com。