改进区域分割的多聚焦图像融合方法*

胡开群，冯 鑫

(1.重庆工商大学 制造装备机构设计与控制重庆重点实验室,重庆 400067；2.重庆市国际科技合作基地装备系统服役健康保障国际联合研究中心，重庆 400067)

改进区域分割的多聚焦图像融合方法*

胡开群1,2，冯 鑫1,2

(1.重庆工商大学 制造装备机构设计与控制重庆重点实验室,重庆 400067；2.重庆市国际科技合作基地装备系统服役健康保障国际联合研究中心，重庆 400067)

针对传统多尺度几何分析方法在图像融合时易损失清晰度以及融合规则选取复杂的缺点，提出一种改进基于区域分割的多聚焦图像融合方法；首先，根据提升静态小波变换快速获得初始融合图像，并对初始融合后的图像进行Normalized Cut算法处理以获得不同的分割区域，然后分别对原始图像进行NSCT变换并计算每个分割区域内高频分量系数的绝对值之和，最后选取绝对值最大的区域为融合后区域，并通过遍历每个分割区域获得融合后的多聚焦图像；数值试验证明，本算法不但融合规则选取较传统多尺度分析融合算法简单，还能够有效克服清晰度损失的缺点，具有有效性。

提升静态小波变换；Normalized Cut算法；NSCT变换；图像融合

0 引 言

基于光学镜头在景深上的限制，可见光成像系统很难将拍摄场景中距离差异较大的所有目标都清晰成像[1]。但是，经过多聚焦图像的融合技术的处理，可以将同一场景中不同焦距的目标融合成一幅所有目标都清晰的新图像，更有利于人眼的视觉观察或是计算机的后续处理[2]。

目前，大多数的多聚焦图像融合技术研究都是在像素层进行展开的。其相关算法大致可以分为两大类：一类为基于空间域图像融合方法；另一类为基于变换域图像融合方法。变换域图像融合方法首先要对待融合图像进行某种框架结构的多尺度几何变换，例如：小波变换(Wavelet Transform，WT)、轮廓波(Contourlet Transform，CT)变换、剪切波变换(Shearlet Transform，ST)等[3-7]，然后经过某种融合规则对待融合图像变换后的分解系数进行组合，获取融合后的变换系数，最后通过多尺度几何分析逆变换获得最终的融合图像[8]。基于多尺度几何分析的融合方法也因为与人类视觉系统的由粗到细认识事物的过程类似而具有比较好的融合效果[9]。但是该类融合方法具有两个较为明显的缺点：由于在融合过程中系数的丢失，该类方法在清晰程度上有不同程度的损失；融合过程中的规则选取具有复杂性，目前没有一种统一有效的多尺度变换融合规则。因此，本文提出一种新的多聚焦图像融合方法，可以避免以上两个问题，并且实验结果表明，方法不会造成清晰度损失，避免了复杂的融合规则选取，具有有效性。

1 基于提升静态小波区域分割的图像融合方法

融合方法的框图如图1所示。

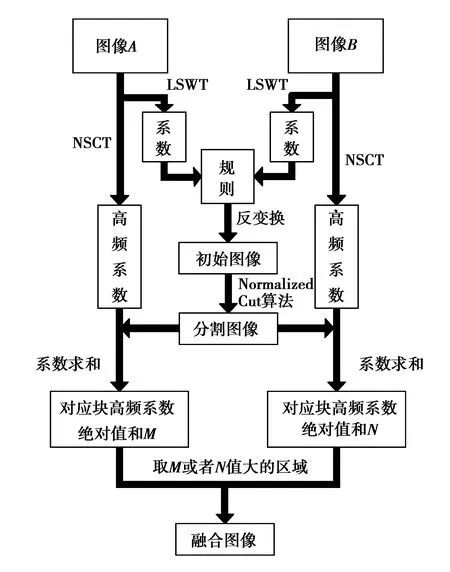
图1 融合方法框图Fig.1 Fusion method diagram of this paper

根据图1所示，本文融合步骤如下：

(1) 根据提升静态小波变换(Lifting Stationary Wavelet Transform，LSWT)快速获得融合后的初始图像，其结果用于下一步的图像分割，使得在图像分割中能够考虑所有输入图像信息。

(2) 对融合后的初始图像进行平滑处理，然后进行通过Normalized Cut算法进行图像分割。

(3) 分别对源图像进行NSCT变换分解，获得与源图像大小相同的系数矩阵。

(4) 求每个分割区域内高频系数绝对值之和，并选取值大的区域为融合后的相应区域。

(5) 遍历所有分割区域，获得最终融合图像。

1.1 初始融合

LSWT变换是一种相对柔性的静态小波变换方法，可以使用线性和非线性的预测算子来确保变换的可逆性。与经典的小波变换不同，LSWT变换具有平移不变性，并且由于其结构简单而具有更好的实时性。图像经过LSWT变换分解后的系数子带图像大小与源图像大小相同，所以能够更好地确定各子带系数图像之间关系，对于融合算法的实现非常有利于[10]。对比融合算法中较优异的非下采样轮廓波(Non-subsampled Contourlet Transform，NSCT)变换和Shearlet变换等经典的多尺度几何分析工具，LSWT变换性能虽然稍弱，但是其运算更加简单。根据对融合性能与运算复杂性等因素的综合考虑，本文选用LSWT变换来进行初始融合。

由文献[11]，两级LSWT变换分解的正向流程如图2所示，其中LP1与HP1表示第一级分解获取的低频和高频系数；LP2与HP2表示第二级分解后获取的低频与高频系数。Us(zl)与Ps(zl)分别为第l(其中，l=1,2,…，n)层数的更新与预测算子。

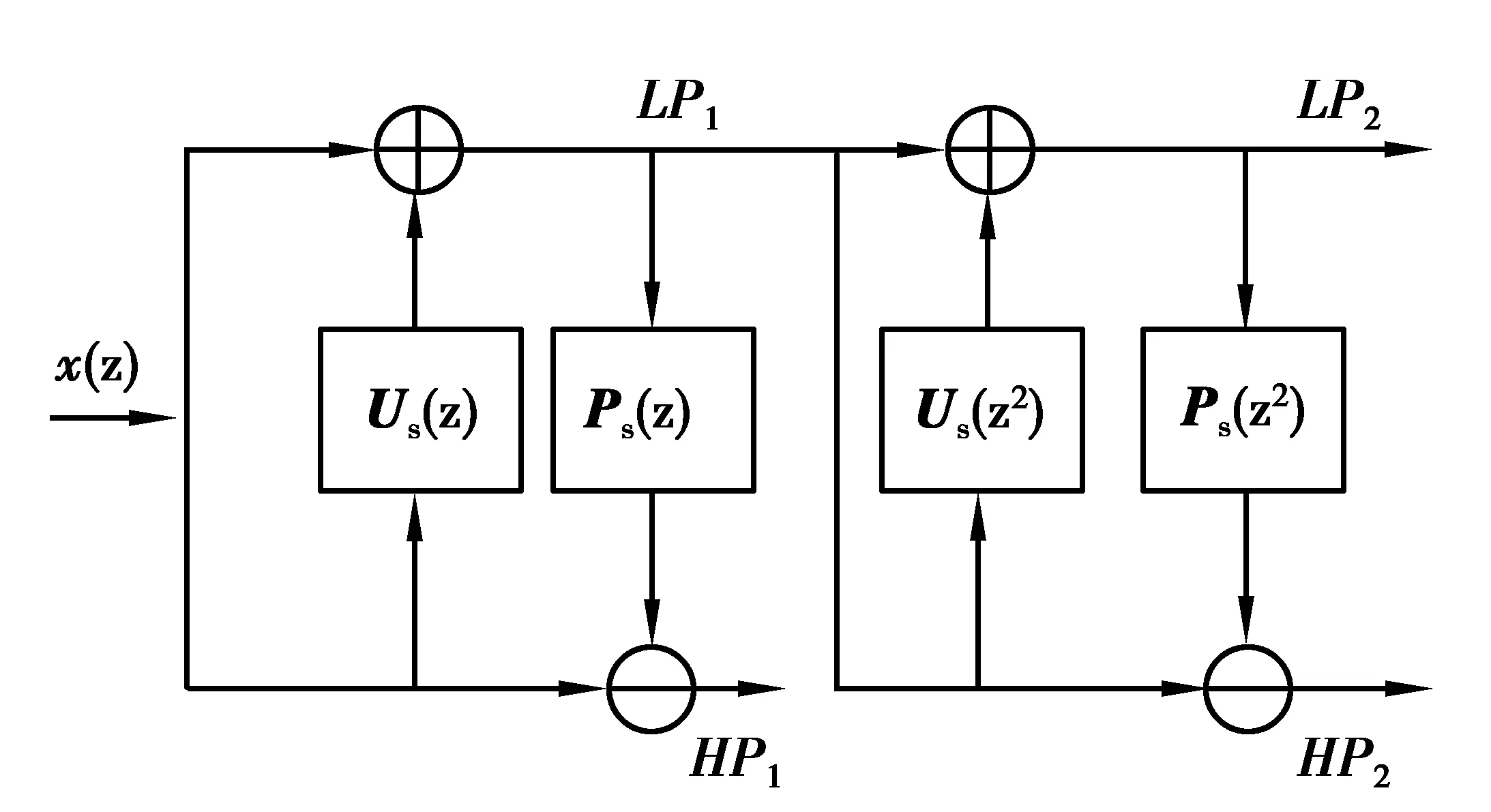
图2 LSWT的二级分解示意图Fig.2 Two-stage decomposition schematic diagram of LSWT

以对图A和图B进行融合为例，其初始融合过程可由图3所示。

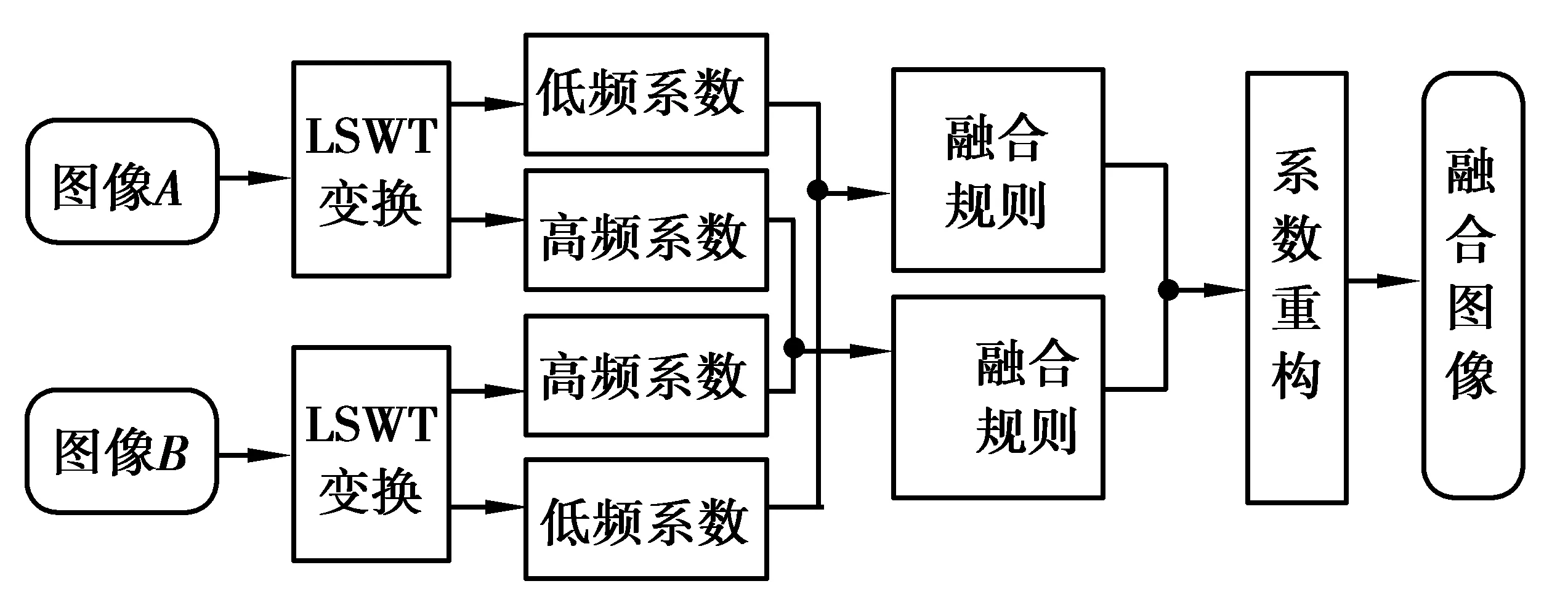
图3 初始融合框图Fig.3 The initial fusion diagram

为了降低算法的复杂性，本文初始融合在低频系数和高频系数的规则上选用最为简单的取平均值的融合规则。

1.2 Normalized Cut算法

Normalized Cut[12]算法是一种规格化形式的方法，它所得到的划分子图内部具有较大相似性，而各个子图之间具有较小相似性。本文Normalized Cut算法目的是将初始融合图像划分为不同的区域。

首先，设w(i,j)为两像素点i和j之间的相似度。其值主要与两像素点之间的亮度值、相对距离、边缘和纹理等因素有关。考虑到算法的复杂性，文中只考虑像素点亮度和相对距离，两像素点i和j之间的亮度距离越小或者空间距离越近，说明w(i,j)的值越大，本文定义权值w(i,j)为

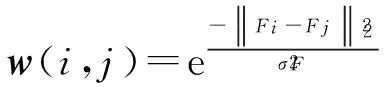
(1)

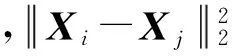
由文献[13]，最小化Normalized Cut算法相当于求解如下的矩阵特征方程：

(D-W)y=λDy

(2)

其中W表示式(1)中所定义n*n的对称矩阵，D表示对角矩阵，且D(i,j)=di。在求解上，y为指示向量，式(2)的次小的特征值对应的特征向量可以看作分割不连通子集A和B的解。

所以本文分割步骤如下：

(1) 根据式(1)计算待分割图像任意两像素点i和j的相似度，即两点间连线的权重ω，并建立其对应的无向图；

(2) 求解式(2)中的次小特征值所对应的特征向量；

(3) 选取适当的阈值将次小特征值的特征向量分成两个部分，相应的将图像分为A和B两个子图像；

(4) 最后判断是否需要进行迭代分割，如需要则跳到第(2)步进行迭代，否则结束。

1.3 NSCT分解

本节采用NSCT变换对初始融合图像A和图像B分别进行多尺度和多方向分解，获得各自的高频子带系数与低频子带系数，如图4所示。

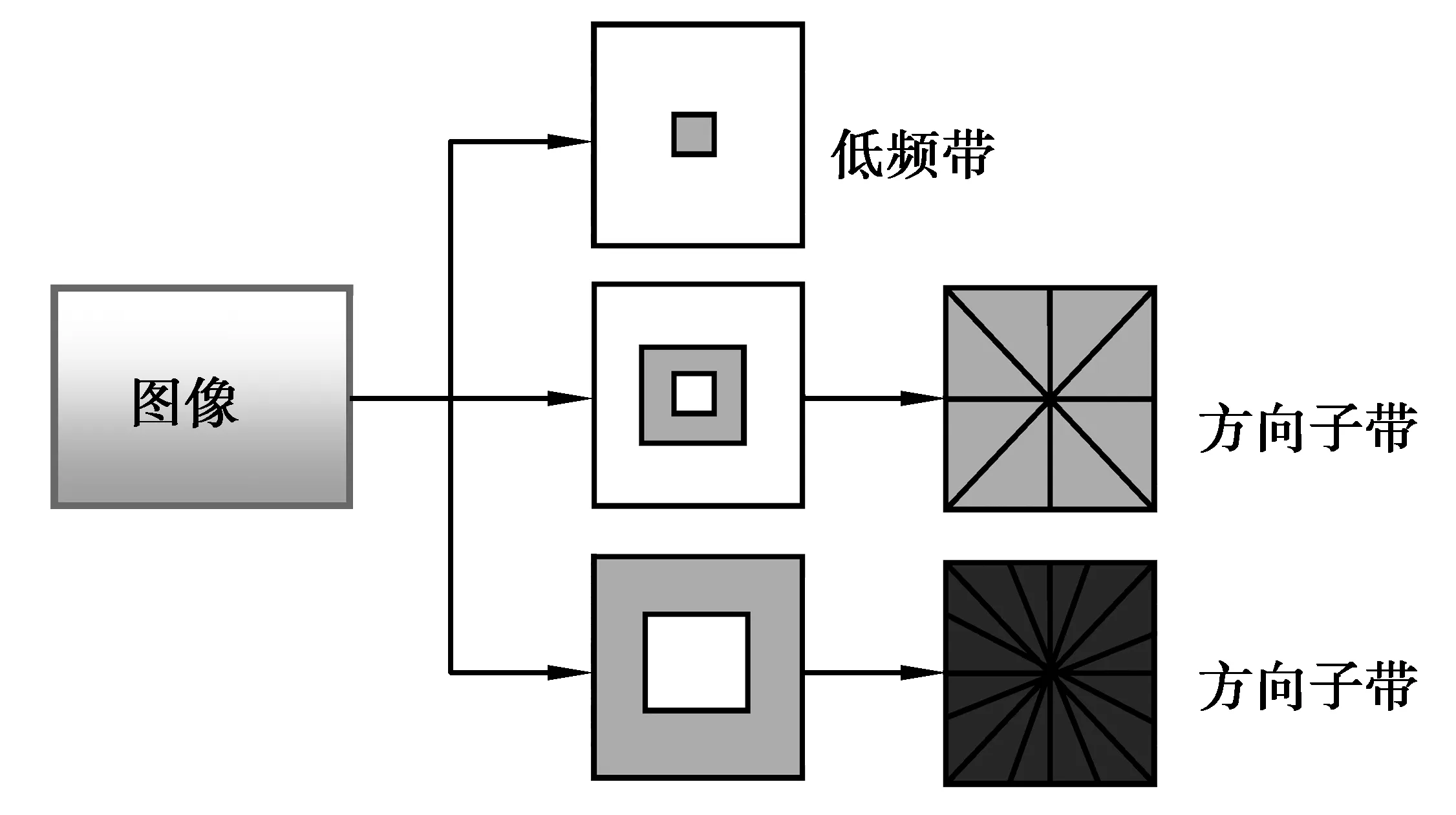
图4 NSCT分解示意图Fig.4 NSCT decomposition schematic diagram

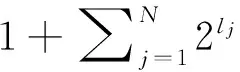
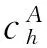
1.4 融合规则

对初始图像进行1层NSCT变换分解，分别得到其高频细节信息和低频近似信息。其中，高频细节信息主要表示源图像的梯度信息，绝对值越大则说明其对应像素值在初始图像中变化越强，该像素值肯定越清晰。所以，本文计算每初始图像中每一个分割区域所对应的NSCT变换分解系数的高频部分绝对值之和，以此来判定该分割区域在源图像的清晰程度，如果绝对值之和越大表示该区域越清晰。本文分别定义源图像A和B中第k个区域中清晰度测量值：

(3)

(4)

其中，ROAk与ROBk分别表示源图像A和B中对应的第k个分割区域。

然后，对两幅图像对应分割区域的清晰度大小进行比较，清晰度大则表示该区域所映射的源图像要比另一幅图像清楚。直接选取该清晰区域为融合结果的相应区域。

(5)

其中，RoFk表示图像F的第k个区域。遍历k个分割区域，最终获得所需融合图像。

2 实验结果

为了验证算法在多聚焦图像融合中的有效性，采用Matlab 2009软件对2组经过配准后的多聚焦图像进行实验仿真，2组源图像选取大小均为512×512，像素灰度级数为256，并采用提升静态小波变换(LSWT)融合方法、NSCT变换融合方法以及Shearlet变换融合方法来进行性能比较[12]。LSWT变换融合方法采用3级分解(l=3)，为降低计算复杂性，在低频部分采用取平均值的简单融合规则，高频部分采用模值取大的融合规则。NSCT变换采用4层分解，其中方向分解滤波器采用“dmaxflat”滤波器，尺度分解滤波器采用“maxflat”滤波器[15]，由粗到细的方向分解级数为2，3，3，4；融合规则同LSWT变换。Shearlet变换方法采用文献[15]中参数进行。

图5 多聚焦图像融合结果对比(1)Fig.5 The contrast of fusion result for multi-focus images(1)

第一组多聚焦图像融合结果如图5所示，其中图5(a)为右清晰的原始钟表图像，图5(b)为左清晰的原始钟表图像。图5(c)～(f)分别为LSWT变换融合方法、NSCT变换融合方法、Shearlet变换融合方法以及本文融合方法进行多聚焦图像融合的结果。由结果可以看出，LSWT变换由于具有平移不变性，所以能较好克制图像融合时可能出现的吉布斯现象，但是由于融合规则简单，待融合图像的目标边缘轮廓清晰度保留较差，钟表盘上的字迹很模糊，唯一的优势是具有很高的实时性。NSCT变换方法融合结果相对LSWT变换方法边缘轮廓信息更加丰富，这说明了NSCT变换在图像边缘轮廓的表示上比一般小波基更强。而Shearlet变换方法由于剪切操作的方向不受限制，所以能在更多方向上分解图像，并利用其快速系数衰减以及能以任意比例尺度对图像边缘逼近的能力，能够获得更加高的对比度和目标边缘轮廓细节。本文方法在LSWT变换融合的基础上，通过简单的Normalized Cut算法并引入NSCT变换对源图像清晰区域进行选定，算法简单，几乎没有清晰度损失，并且NSCT变换无需重构步骤，降低了计算复杂度。所以，本文方法相对具有最高的清晰度和最好的边缘细节信息。

图6 多聚焦图像融合结果对比(2)Fig.6 The contrast of fusion result for multi-focus images(2)

第二组多聚焦图像融合结果如图6所示，其中图6(a)与图4(b)分别为原始图像。图6(c)～(f)分别为LSWT变换融合方法、NSCT变换融合方法、Shearlet变换融合方法以及本文融合方法对多聚焦图像进行融合的结果。从融合结果来看，几种方法都能够很好消除源图像的聚焦差异，得到的图像前景和背景都比较清晰。但是通过对融合结果的仔细比对和研究，提出算法的融合综合性能是最好的。LSWT变换方法由于融合规则选取简单，相对于源图像来说损失了一部分的清晰度，且有比较明显的噪声信号，尤其是在高频纹理比较丰富的部分。NSCT变换方法由于变换框架具有平移不变性，所以虚假信息得到了较好的抑制。Shearlet变换法与本文方法相比，清晰程度明显要低，目标轮廓没有本文方法融合结果清晰，并且本文算法同样在NSCT变换域中进行，也具有平移不变性，能够对原始图像中的虚假噪声信号进行有效抑制。所以综合看来，本文方法无论是在对比度的保持还是吉布斯现象去除上都有一定的优势。

图7为本文方法以及所采取的对比方法得到的融合图像进行局部区域放大后的结果，可以清晰地看到，本文采用的区域分割算法所获的融合结果不仅保留了多聚焦目标的边缘，也克服了边缘吉布斯效应，主观效果最好。

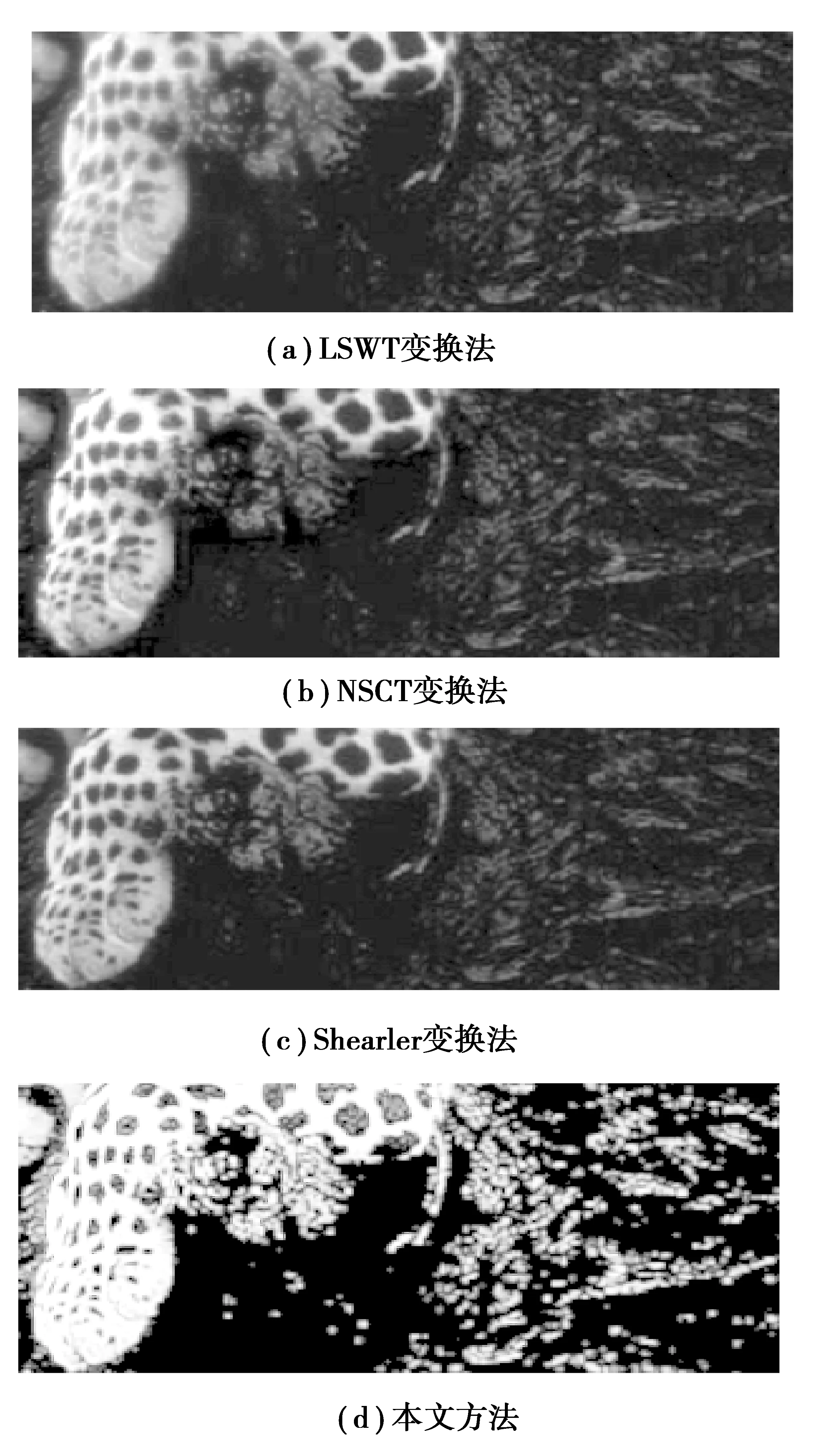
图7 局部放大对比图Fig.7 The contrast of fusion result for local zoom images

为了对图像融合质量进行客观评价，本文选用信息熵(Information Entropy，IE)、互信息(Mutual Information，MI)、峰值信噪比(Peak Signal to Noise Ratio，PSNR)、边缘信息保留量(QAB/F)以及程序花费时间T(s)等5种量化指标对所获融合结果进行评价。其量化指标表示如下。

图像的信息熵可以用来衡量图像信息是否丰富，定义为

(6)

其中，L表示图像F的灰度级，pi表示灰度级i的分布概率。

互信息定义了两幅图像A和B之间的相关性。源图像A和融合所得图像F之间的互信息定义为

(7)

其中，hAF(i,j)为源图像A和融合图像F的归一化联合灰度直方图，hA(i)和hF(j)是两幅图像的归一化直方图，L为灰度级数。同理，图像B与融合图像F之间互信息用MIBF表示。图像融合结果的互信息可以定义为

MI=MIAF+MIBF

(8)

峰值信噪比用来衡量融合后图像的清晰程度，定义为

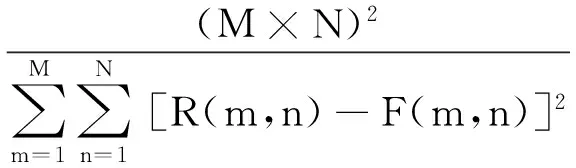
(9)

边缘信息保留量(QAB/F)用来评价源图像传递到融合图像的边缘信息量。

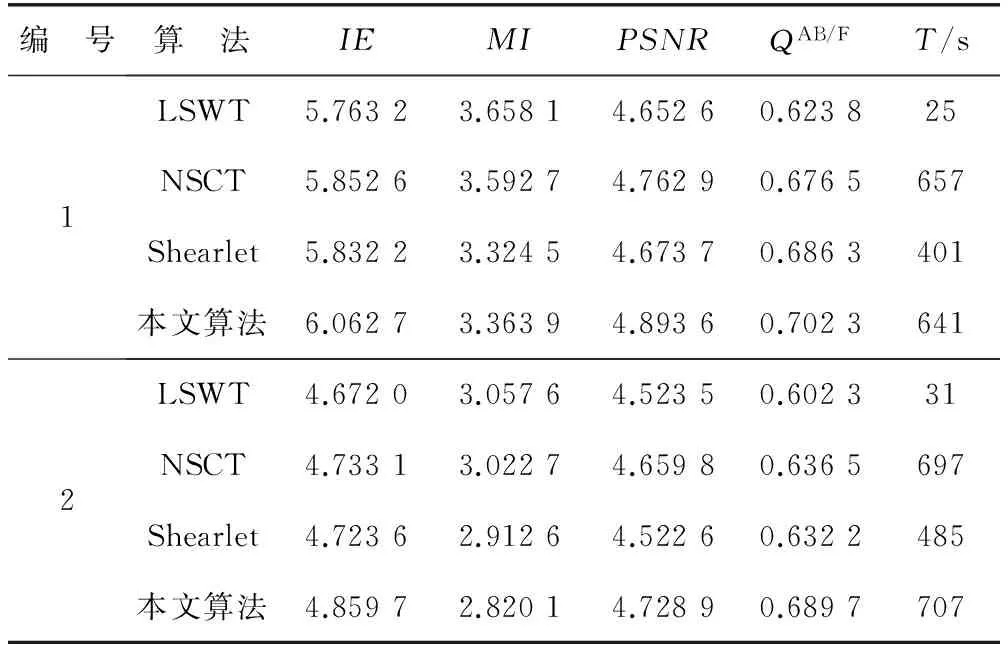
表1 各种融合结果的量化比较Table 1 Quantitative comparison of the fusion results with different methods

由表1可以看出，在量化指标上，本文融合方法在IE、MI、PSNR、QAB/F4项[16]上均为最好。由于不需进行重构操作，所以本文算法在运行时间耗费上也仅多于LSWT变换方法，相比其他两种多尺度几何分析融合方法要少，证明了本文方法在运算复杂度上也具有一定的优越性。

3 结 论

针对多聚焦图像的特性，提出一种改进的区域分割融合方法。首先引入提升静态小波快速获得融合初始图像，对初始融合图像进行简单的Normalized Cut算法分割后，选取其NSCT变换系数绝对值之和为融合规则，实验表明，本文方法不会损失清晰度，并且避免了复杂的融合规则选取，具有有效性。

[1] 刘斌,刘维杰,马嘉利.基于三通道不可分对称小波的多聚焦图像融合[J].仪器仪表学报.2012，33(5)：1110-1116

LIU B,LIU W J,MA J L.Multi-focus Image Fusion Based on Three Channel Non-separable Symmetrical Wavelets[J].Chinese Journal of Scientific Instrument.2012,33(5):1110-1116

[2] 王刚,马美仲,赵英路.Curvelet 变换域的图像融合算法[J].仪器仪表学报,2008,29(9):1841-1845

WANG G,MA M Z,ZHAO Y L.Algorithm for Image Fusion in the Curvelet Transform Domain[J].Chinese Journal of Scientific Instrument,2008,29 (9):1841-1845

[3] LI S T,YANG B,HU J W.Performance Comparison of Different Multiresolution Transforms for Image Fusion[J].Information Fusion,2011,12(2):74-84

[4] DO M N,VETTERLI M.The Contourlet Transform:An Efficient Directional Multiresolution Image Representation[J].IEEE Transactions Image on Processing,2005,14(12):2091-2106

[5] EASLEY G，LABATE D，W Lim.Sparse Directional Image Representations Using the Discrete Shearlet Transform[J].Applied and Computational Harmonic Analysis,2008,25(1):25-46

[6] CUNHA D A L,ZHOU J P,M N Do.The Non Subsampled Contourlet Transform:Theory,Design,and Applications[J].IEEE Transaction on Image Processing,2009,15(10):3089-3101

[7] 江铁,朱桂斌,孙奥.全景图像拼接技术研究现状综述[J].重庆工商大学学报(自然科学版),2012,29(12):60-67

JIANG T,ZHU G B,SUN A.Review of Research Status of Panoramic Image Mosaic Technology [J].Journal of Chongqing Technology and Business University (Natural Science Edition),2012,29(12):60-67

[8]DEMANET L,Ying L X.Wave Atoms and Sparsity of Oscillatory Patterns[J].Applied and Computational Harmonic Analysis,2007,23(3):368-387

[9] 郑红,郑晨,闫秀生.基于剪切波变换的可见光与红外光图像融合算法[J].仪器仪表学报,2012,33(7):1613-1619

ZHENG H,ZHENG C,YAN X S.Visible and Infrared Image Fusion Algorithm Based on Shearlet Transform[J].Chinese Journal of Scientific Instrument.2014,33(7):1613-1619

[10] ZHANG W,YANG J Z,WANG X H.The Fusion of Remote Sensing Images Based on Lifting Wavelet Transformation[J].Computer Information Science,2009,2(1):69-75

[11] CHAI Y,LI H F,QU J F.Image Fusion Scheme Using a Novel Dual-Channel PCNN in Lifting Stationary Wavelet Domain[J].Optics Communications,2010,283(19):3591-3602

[12] COUR T,BENEZIT F,SHI J B.Spectral Segmentation with Multiscale Graph Decomposition∥[C]Proceedings of IEEE Conf Computer Vision and Pattern recognition,Philadelphia,PA,USA,2005,2:1124-1131

[13] 杨斌.像素级多传感器图像融合新方法研究[D].长沙:湖南大学,2010

YANG B.Researches on Novel Methods for Pixel Level Multi-sensor Image Fusion[D].Changsha:Hunan University,2010

[14] 冯鑫,王晓明.基于插值Directionlet变换的图像融合方法[J].吉林大学学报(工学版),2013,43(4):1127-1132

FENG X,WANG X M.Image Fusion Method Based on Interpolation Directionlet[J].Journal of Jilin University(Engineering and Technology Edition),2013,43(4):1127-1132

[15] MIAO Q G,SHI C,XU P F.Multi-Focus Image Fusion Algorithm Based on Shearlet[J].Chinese Optics Letter,2011,9(4): 121-126

[16] QU G,ZHANG D L,YAN P F.Information Measure for Performance of Image Fusion[J].Electronic Letters,2002,38(7):313-315

Multi-focus Image Fusion Method Based on Improved Regional Segmentation

HUKai-qun1,2,FENGXin1,2

(1.Chongqing Key Laboratory of Manufacturing Equipment Mechanism Design and Control,Chongqing Technology and Business University,Chongqing 400067,China; 2.International Joint Research Center of Chongqing International Technology Cooperation Base for Equipment System Service Health Care,Chongqing 400067,China)

According to the shortcoming that traditional multi-scale geometry analysis method is easy to lose clarity and hard to choose fusion rules when an image is fusing,this paper proposes an improved multi-focus image fusion method based on regional segmentation,firstly,uses Lifting Stationary Wavelet Transform to obtain the initial fused images,then receives different segmented regions by treating the initial fused image with Normalized Cut algorithm,uses NSCT transform for the original images respectively,calculates the sum of absolute value of transform coefficient of each segment of high frequency component,finally chooses the biggest absolute value area for fused area,and obtains fused multi-focus image by iterating through each segmented region.Numerical example proves that this algorithm is not only more simple in choosing fusion rules than traditional multi-scale analysis fusion algorithm but also can overcome the shortcoming of clarity loss and has validity.

Lifting Stationary Wavelet Transform; Normalized Cut algorithm; NSCT transform; image fusion

TP391

：A

：1672-058X(2017)05-0043-07

责任编辑：罗姗姗

10.16055/j.issn.1672-058X.2017.0005.008

2017-05-17；

：2017-07-03.

重庆市教委基础与前沿研究计划项目(KJ1500635)；重庆工商大学引进人才科研启动基金(2013-56-06)，重庆市教委基础与前沿研究计划项目(KJ1400628).

胡开群(1981-)，女，重庆巴南区人，讲师，博士，从事计算机测控与图形处理研究.