求解自由边界问题的自适应投影方法*

钟艳丽,严月月,钟思超

(重庆师范大学 数学科学学院,重庆 401331)

求解自由边界问题的自适应投影方法*

钟艳丽,严月月,钟思超

(重庆师范大学 数学科学学院,重庆 401331)

对一类自由边界问题，提出了基于线性互补问题的自适应投影算法.采用有限差分格式将自由边界问题离散为一个线性互补问题，然后用自适应投影迭代算法求其数值解，该方法在迭代过程中自动调整参数，达到加快收敛速度的目的，每一步迭代只需要求解一个线性方程组.给出了具体算法过程，并利用投影性质得到了它们的收敛性分析.最后用数值算例对算法验证，与已有的算法比较，结果表明：参数对自适应投影算法影响较小，该方法收敛速度更快.

自由边界问题；有限差分；线性互补；自适应投影法

自由边界问题在所考虑区域内部的微分方程是非线性的，通常不存在精确解或很难求其精确解，因此需要用数值方法求解.目前已有的方法有有限差分法、有限元法等[1-5].文献[3]用有限差分法将求解的问题离散为线性互补问题，提出了投影算法.本文将障碍问题离散成有限维的线性互补问题，该问题等价于一个投影不动点问题[6-8]，其中采用由迭代数据自动选取参数ρ的办法，从而得到了自适应投影算法.给出了具体的算法过程和收敛性分析，通过若干数值算例对不同方法进行了比较研究.

1 自由边界问题及其有限差分格式

有以下问题：

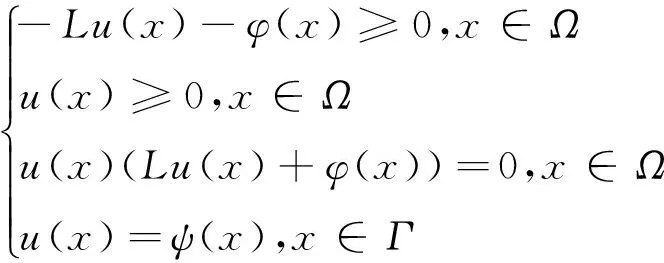
(1)

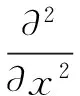
且该变分不等式有唯一解[1,9-14],即问题(1)有唯一解.

首先采用有限差分对问题(1)中的微分算子离散化得:

(2)

其中向量函数z表示未知函数u在网格节点上的近似值.对问题(2)代入已知区域Ω内的函数φ(x)和边界Γ上的函数ψ(x),则问题(1)可改写为标准的有限维线性互补问题:

z≥0,Mz+q≥0,〈z,Mz+q〉=0

(3)

其中向量q的元素依赖于已知函数ψ(x)及φ(x).定义非空有界闭凸集:

C:={z∈RN|zi≥0}(i=1,2,…,N)

则由文献[8]知互补问题(3)等价于向量变分不等式:

〈z-z*,Mz*+q〉≥0,∀z∈C

当n=1即一维情形时，将区间[a,b]进行N+1等分，则内节点数目为N，z为函数u(x)在区域Ω内网格节点待求函数值构成的N维列向量，M∈RN×N为三对角矩阵，q∈RN为已知N维列向量，当数目为N2,则M∈RN2×N2为三对角分块矩阵[8,14]，z为函数u(x)在区域Ω内网格节点待求函数值构成的N2维列向量.特别地，本文对差分算子使用等步长的差分格式，则矩阵M为对称正定稀疏矩阵，从而由文献[8]知上述有限维向量变分不等式和极小值问题有唯一解.

2 自适应投影算法和收敛性分析

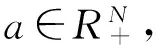
Mz+q=[(Mz+q)-ρz]+(ρ>0)

此问题又等价于求解:

e(z,ρ):=Mz+q-[(Mz+q)-ρz]+

的零点.文献[2-5]由这个不动点问题出发得到一系列问题(1)的投影算法.由于不动点问题e(z,ρ)=0又等价于Mz+ρz=Mz+ρz-ωe(z,ρ)，其中参数ω∈(0,2),故有求解问题(2)的投影算法:

Mzk+1+ρzk+1=Mzk+ρzk-ωe(zk,ρ)

参数ρ取太小或太大，迭代的次数或迭代时间可能增加很多.为了改进这种方法,可以考虑一种比较普遍的方法如自适应算法，该方法通过在迭代过程中自动调整参数，用变量序列{ρk}代替常量参数ρ.下面考虑如何得到变量序列{ρk}.在此之前,有以下假设成立：问题(3)的解集为Ω*且是非空的.

对于给定的zk，新迭代的zk+1，都是由投影算法得到的.

M(zk+1-zk)+ρ(zk+1-zk)=-ω(e(zk,ρ))

问题(3)的解对于ρk(ρk>0)是不变的[9]，所以有

M(zk+1-zk)+ρk(zk+1-zk)=-ω(e(zk,ρk))

然而为了保持平衡，希望

为了找到一种方法去选择参数ρk，给定常数α>0，如果

那么在下次迭代时ρk要增加.如果

那么在下次迭代时ρk要减少.令

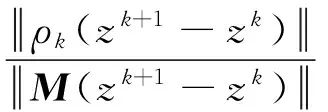
然后,让

上面的α是给定的正数.

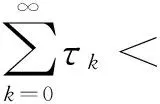
用ck计算{ρk}改变的的次数，令

采用如此方法得到非负序列{τk}：

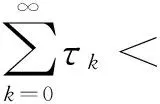
下面给出算法.

算法1：自适应投影算法.

第3步：计算zk+1=zk-ω(ρkI+M)-1e(zk,ρk),得zk+1.

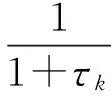
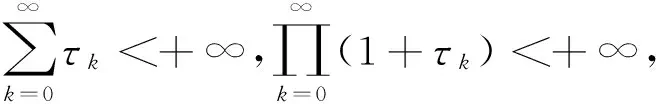
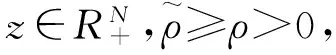
(4)

证明首先，要证式(4)只需证

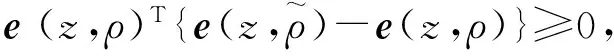
利用凸集上的投影性质：

(a) (v-PΩ[v])T(PΩ[v]-u)≥0.

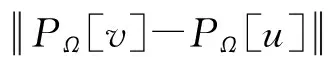
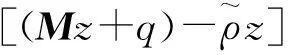
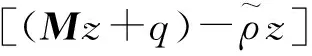
又因为

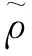
(5)

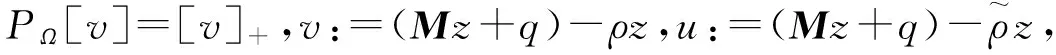
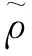
(6)

利用式(5)(6)，可得

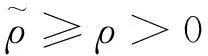
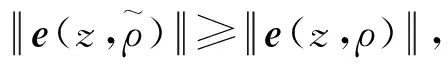
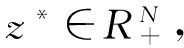
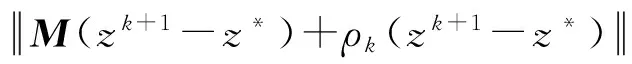
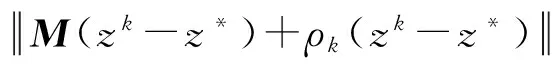
(7)

证明由自适应投影算法

Mzk+1+ρkzk+1=Mzk+ρkzk-ωe(zk,ρk)

及引理1得：

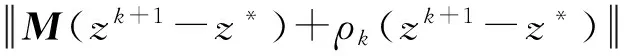
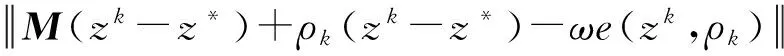
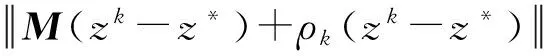
2ω〈M(zk-z*)+ρk(zk-z*),e(zk,ρk)〉≤

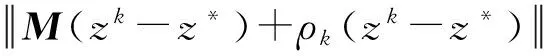
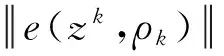
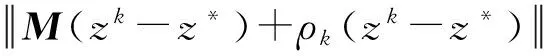
显然有

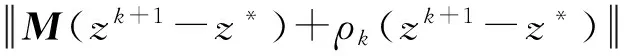
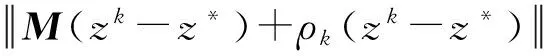
证毕.

因为0<ρk+1≤(1+τk)ρk,所以

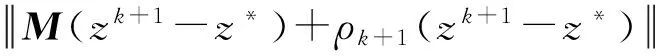
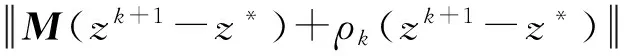
(8)

联合式(7)(8)，有

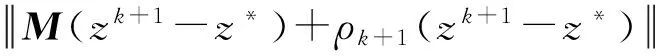
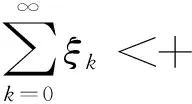
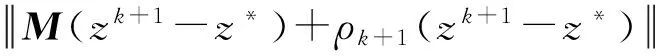
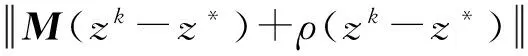
(9)

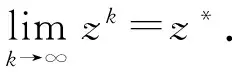
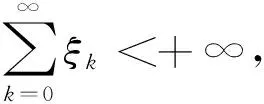
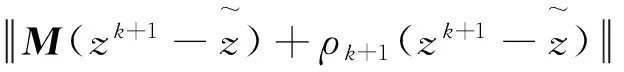
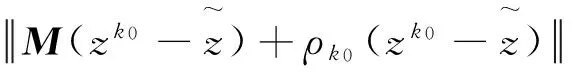
因此，存在常数C>0，有

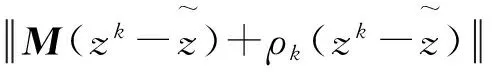
(10)

显然{zk}是有界的，利用式(9)(10)，则

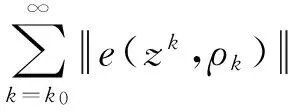
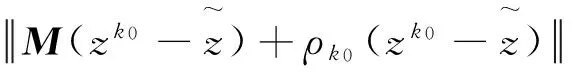
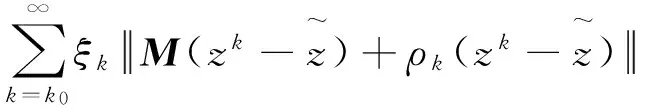
设z*是{zk}的一个聚点且子序列{zkj}收敛于z*，因为e(z,BL)是连续的，则有

所以z*是问题(3)的一个解.

假设z**≠z*是{zk}的另一个聚点，因为z*是{zk}的聚点，所以存在k1>k0,使得

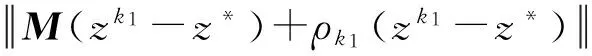
由式(9)可知，对任意k>k1，有

因此，有

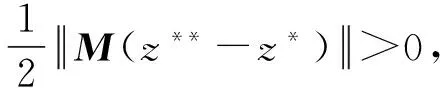
显然与假设矛盾，因此z**不是{zk}的聚点，即{zk}收敛于z*，证毕.

3 算例分析

为了检验自适应投影算法的性能，对该方法进行数值验证.

例1 考虑Ω=[0,4]中的一维问题[11]：

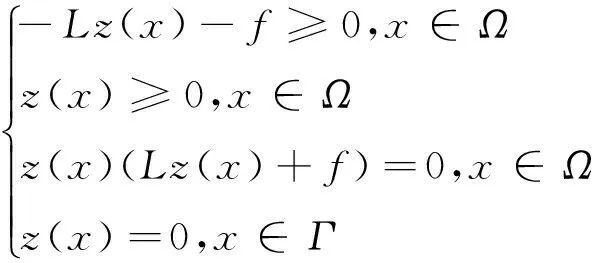
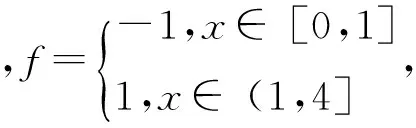
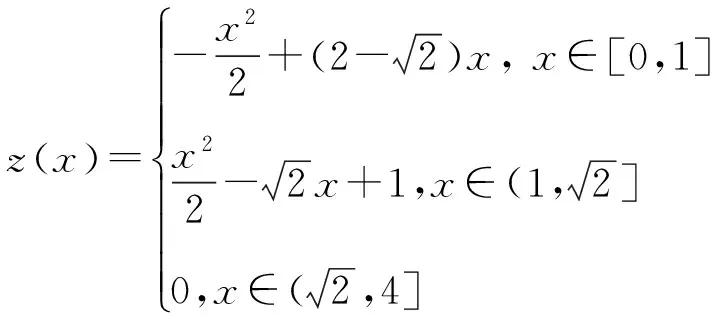
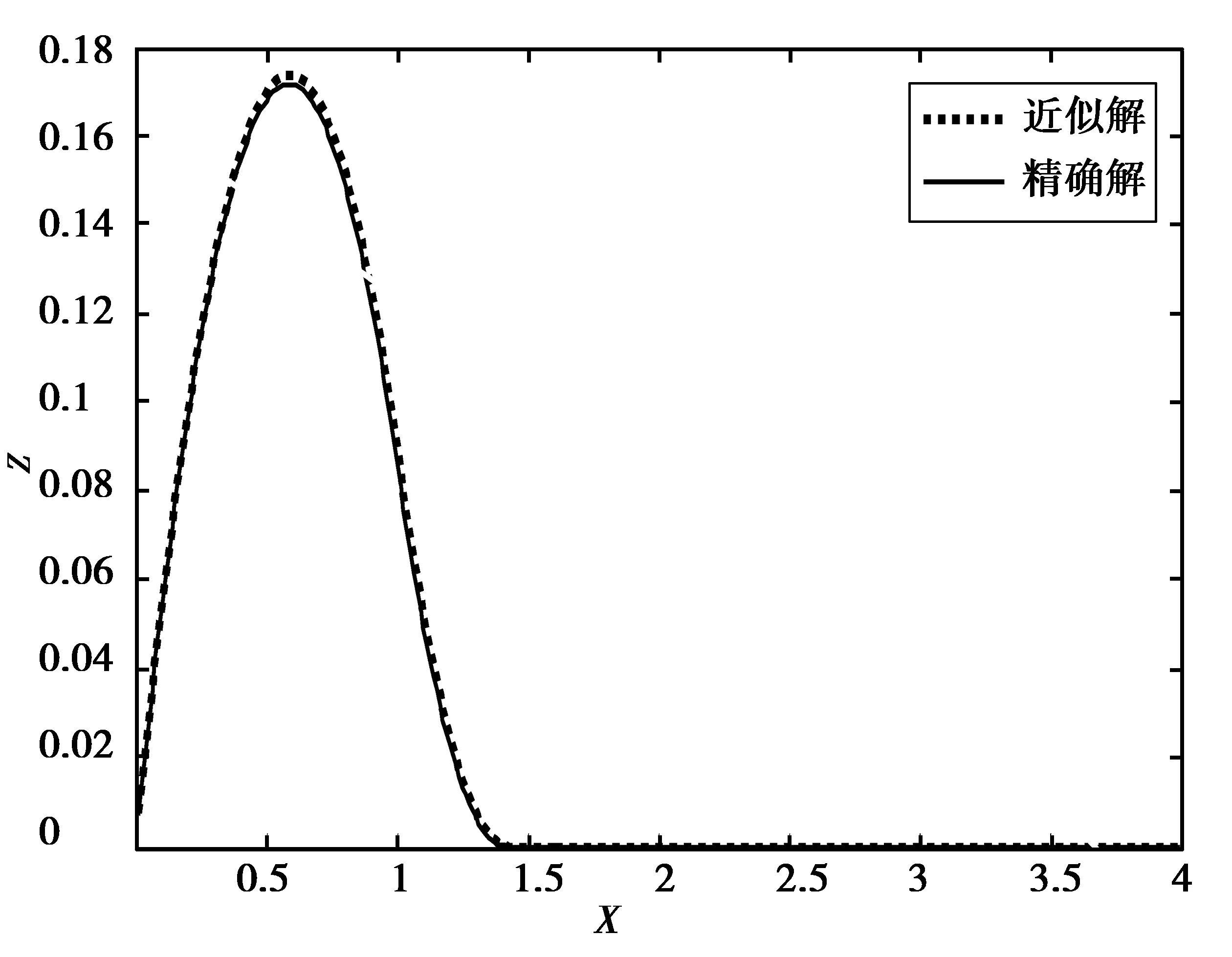
图1 例1数值解结果Fig.1 Numerical results of example 1

表1 两种不同算法关于迭代次数n的比较Table 1 The comparison of two algorithms about the number of iterations n

以上“fail”表示迭代次数超过1 000次，N表示网格节点数，以上自适应算法中取ω=1.8，由表1可知，文献[4]中的算法与自适应投影算法相比，可以看出参数ρ的选取对自适应投影算法无大的影响，自适应投影算法比较稳定，并且迭代次数比较小，收敛速度相对较快.

例2 考虑在正方形区域Ω=(-1.5,1.5)×(-1.5,1.5)中的二维问题[2,5]:

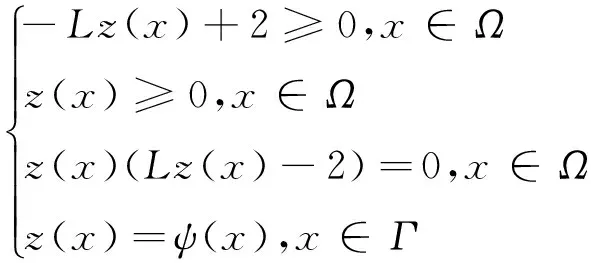
图2 例2数值解结果Fig.2 Numerical results of example 2

表2 两种不同算法关于迭代次数n的比较Table 2 The comparison of two algorithms about the number of iterations n

以上“fail”表示迭代次数超过1 000次，N2表示网格节点数，以上自适应算法中取ω=1.8，由表2可知，文献[4]中的算法与自适应投影算法相比，可以看出参数ρ的选取对自适应投影算法无大的影响，自适应投影算法比较稳定，并且迭代次数比较小，收敛速度相对较快.

4 结 论

提出了求解自由边界问题的算法——自适应投影算法，该算法采用中心差分格式将自由边界问题离散为一个线性互补问题，在投影迭代的基础上自动调整参数，不仅加快了收敛速度且求出了数值解.在用数值算例对算法进行的比较中，结果表明参数对自适应投影算法影响较小，该方法收敛速度更快.

[1] 韩渭敏,程晓良.变分不等式简介:基本理论数值分析及应用[M].北京:高等教育出版社,2007

HAN W M,CHENG X L.Introduction to Variational inequation[M].Beijing:Higher Education Press,2007

[2] 张守贵.求解自由边界问题的投影收缩算法[J].重庆师范大学学报(自然科学版),2015,32(2):50-52

ZHANG S G.A Projection and Contraction Algorithm for the Free Boundary Problem[J].Journal of Chongqing Normal University (Natural Science Edition),2015,32(2):50-52

[3] 张守贵.自由边界问题的线性互补投影迭代算法[J].西南师范大学学报(自然科学版),2013,38(7):15-19

ZHANG S G.The Linear Complementarity Projection Iterative Algorithm for Free Boundary Problem[J].Journal of Southwest China Normal University (Natural Science Edition),2013,38(7):15-19

[4] 张守贵.自由边界问题的自适应预测-校正算法[J].西南师范大学学报(自然科学版),2014,39(9):1-5

ZHANG S G.On a Self-Adaptive Prediction-Correct Algorithm for Free Boundary Problem[J].Journal of Southwest China Normal University (Natural Science Edition),2014,39(9):1-5

[5] BRAESS D,CARSTENSEN C,HOPPE R H W.Convergence Analysis of a Conforming Adaptive Finite Element Method for an Obstacle Problem[J].Numer Math,2007,107:455-471

[6] 何炳生.一类求解单调变分不等式的隐式方法[J].计算学,1998,20(4):337-345

HE B S.A Class of Implicit Methods for Monotone Variational Inequalities[J].Math Numerica Sinica,1998,20(4):337-345

[7] HE B S.Inexact Implicit Methods for Monotone General Variational Inequalities[J].Math Program,1999,86(7):199-217

[8] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006

HAN J Y,XIU N H,QI H D.Nonlinear Complementarity Theory and Algorithm[M].Shanghai:Shanghai Science and Technology Press,2006

[9] HAN D R.Solving Linear Variational Inequality Problems by a Self Adaptive Projection Method[J].Appl Math Comput,2006,182:1765-1771

[10] NOOR M A.Projection-Splitting Algorithms for Monotone Variational Inequalities[J].Comput Math Appl,2000,39:73-79

[11] MERMRI E B,HAN W.Numerical Approximation of a Unilateral Obstacle Problem[J].J Optim Theory Appl,2012,153:177-194

[12] NOOR M A.Splitting Algorithms for General Pseudo-monotone Mixed Variational Inequlities[J].J Global Optim,2000,18:75-89

[13] NOOR M A.Some Developments in General Variational Inequalities[J].Appl Math Comput,2004,152:199-277

[14] LIAN X P,CEN Z D,CHENG X L.Some Iterative Algorithms for Obstacle Problems [J].INT J COMPUT MATH,2010,87(11): 2493-2502

[15] HE B C,LIAO L Z,WANG S l.Self-adaptive Operator Splitting Methods for Monotone Variational Inequalities[J].Mumer Math,2003,94:715-737

A Self-adaptive Projection Algorithm for Solving Free Boundary Problem

ZHONGYan-li,YANYue-yue,ZHONGSi-chao

(School of Mathematical Science,Chongqing Normal University,Chongqing 401331,China)

According to a class of free boundary problems,a self-adaptive projection algorithm based on linear complementarity problem is put forward,The free boundary problem is discretized by the finite difference method and formulated as a linear complementarity problem,then the self-adaptive projection iteration algorithm is used to obtain its numerical solution,this method automatically adjusts parameters in iterative process to attain the goal of accelerating the convergence speed,and this method only needs to solve a system of linear equations for each iteration.The detailed algorithm process is given,their convergence analysis is obtained by projection properties.Finally,the numerical examples are used to test the algorithm,compared with the existed algorithms,this method has more rapid convergence speed because the parameter has little effect on the self-adaptive projection algorithm.

free boundary problem; finite difference; linear cmplementarity; self-adaptive projection algorithm

O241.182

：A

：1672-058X(2017)05-0007-06

责任编辑：李翠薇

10.16055/j.issn.1672-058X.2017.0005.002

2017-03-15；

：2017-04-26.

国家自然科学基金资助项目(11471063).

钟艳丽(1993-)，女，江西宜春人，硕士研究生，从事微分方程数值解法研究.