IIWPSO-PNN在化工过程故障诊断中的应用

谭 莉，于春梅

(西南科技大学信息工程学院，四川 绵阳 621010)

IIWPSO-PNN在化工过程故障诊断中的应用

谭 莉，于春梅

(西南科技大学信息工程学院，四川 绵阳 621010)

概率神经网络(PNN)已成功应用于化工过程故障诊断。在概率神经网络中，平滑参数对网络性能有很大的影响，并且很难确定。因此，采用粒子群优化(PSO)算法，寻找最优平滑参数。针对粒子群优化算法中线性变化的惯性权重易使其陷入局部极值问题，采用非线性变化的惯性权重替代线性变化的惯性权重，并将其应用于改进惯性权重粒子群(IIWPSO)算法。将IIWPSO算法应用于概率神经网络中(即IIWPSO-PNN)，使其自动搜索并寻找最优的平滑参数用于概率神经网络的训练和测试。与前人提出的线性变化惯性权重、两种非线性变化的惯性权重(分别记为w1、w2和w3)进行比较，将w1、w2和w3应用于PSO-PNN中(分别记为PSO-PNN1、PSO-PNN2和PSO-PNN3)。最后将IIWPSO-PNN应用于田纳西-伊斯曼过程中，与PNN、PSO-PNN、PSO-PNN1、PSO-PNN2和PSO-PNN3网络进行比较。试验结果表明：IIWPSO-PNN在解决故障诊断问题时，识别率与收敛速度都有较大的提高。试验结果验证了IIWPSO-PNN算法应用于化工过程的可行性和有效性。

概率神经网络； 故障诊断； 平滑参数； 惯性权重； 粒子群算法； 田纳西-伊斯曼； 化工过程

0 引言

化工过程具有规模大、复杂性高、变量多等特点。为确保化工过程安全可靠地运行、消除故障隐患，对其进行及时、有效的故障诊断非常必要。概率神经网络(probabilistic neural network,PNN)已广泛地应用于各类故障诊断中。Wang等提出采用概率神经网络进行故障诊断，结果表明，识别率与仿真速度明显优于其他网络[1]。

针对概率神经网络平滑参数的问题，Yi等提出自适应策略改进概率神经网络的平滑参数，效果优于PNN网络，但随着自适应的范围逐渐增大，效率逐渐降低[2]。黎群辉等将差异演化算法应用于PNN中，识别率提高，但收敛速度较慢[3]。Porwik等提出粒子群优化(particle swarm optimization-PNN,PSO-PNN)概率神经网络进行识别，效果明显优于PNN网络，并且稳定性提高[4]。因此，本文在PSO-PNN的基础上，将改进惯性权重粒子群(improved inertia weight PSO,IIWPSO)算法应用于PNN网络中，并基于标准化工测试过程——田纳西-伊斯曼过程进行仿真验证。

1 算法描述

1.1 概率神经网络

概率神经网络是基于径向基神经网络发展而来的一种前向性神经网络[5]，1990年由Specht提出，是一种基于贝叶斯规则与Parzen窗的概率密度函数发展而来的并行算法，具有训练时间短、结构固定、非线性识别能力强等特点，特别适合故障诊断以及识别问题[6]。概率神经网络由输入层、模式层、求和层和输出层组成，其网络结构如图1所示。

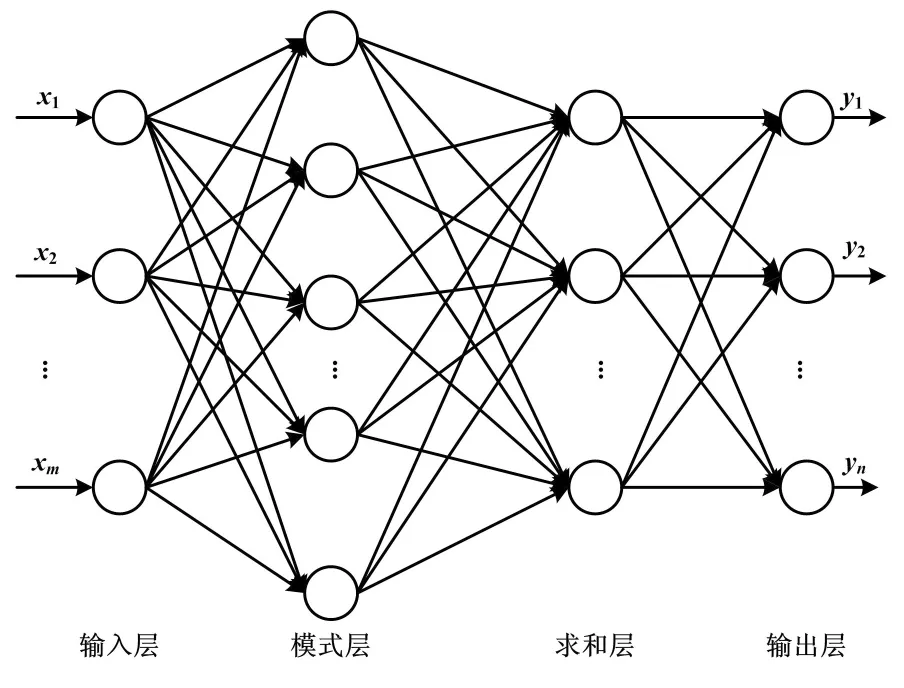
图1 概率神经网络结构图

输入层神经元的数目和训练样本的维数相等，记训练样本为X=(x1,x2,…,xm)T。

模式层计算训练样本X与权值向量IW的距离，通常采用欧氏距离；然后通过径向基非线性映射后获得模式层的输出向量M。径向基函数通常选取高斯函数，输出向量M表示训练样本输出为各类的概率，由式(1)计算，σ为平滑参数。

(1)

求和层计算模式层输出向量M的加权和S，由式(2)计算：

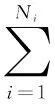
(2)

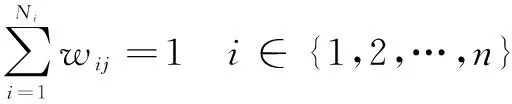
(3)

式中：wij为各向量的权重；n为总的模式数；Ni为i类模式层的神经元数目。

输出层根据求和层的输出S中的最大值，获得网络的输出Q(X)。

(4)

平滑参数决定了以样本点为中心的高斯曲线的宽度，并对网络性能有很大的影响，且在一定范围内有一个值使识别效果达到最好。在概率神经网络中，平滑参数通常是经验设定，需要在多次仿真试验中才能找出使识别效果最好的值。因此，本文提出改进粒子群优化算法寻找最优平滑参数，使其自动搜索并寻找最优的平滑参数，并将其应用于概率神经网络中。

1.2 改进粒子群优化算法

粒子群优化算法是由Kennedy和Eberhart于1995年提出的种群智能优化算法[7]。在粒子群算法中，每个粒子代表寻优空间中一个潜在的解。每一次迭代进化中，粒子通过自身和群体的历史最优位置更新当前的速度和位置，在任意(t+1)时刻，粒子群算法中第i个粒子第d维的速度和位置由式(5)和式(6)更新[8]。

vid(t+1)=wvid(t)+c1r1[pid-xid(t)]+c2r2[pgd-xid(t)]

(5)

xid(t+1)=xid(t)+vid(t+1)

(6)

式中：vid和xid为粒子的速度和位置；w为惯性权重；c1和c2为加速因子，分别代表认知参数和社会参数；pid和pgd分别为个体和群体的历史最优位置；r1和r2为相互独立且服从[0,1]均匀分布的随机数。

w由式(7)计算，wmax为w的最大值；wmin为w的最小值；t为当前迭代步数；Tmax为最大迭代步数[8]。

(7)

当w较大时，全局搜索能力强，局部开发能力弱[9]。因此，在全局搜索算法中，希望前期有较高的全局搜索能力以搜索更大的空间，并定位全局最优的近似位置，而在后期有较高的开发能力，以增强局部搜索能力，加快收敛速度。文献[10]与文献[11]提出的非线性变化惯性权重，其计算公式分别如式(8)和式(9)所示。Nickabadi等提出自适应惯性权重的粒子群算法(adaptive inertia weight PSO,AIWPSO)，具体过程见文献[12]。

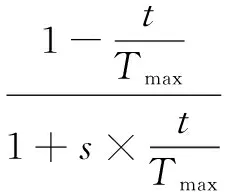
(8)

(9)

本文针对惯性权重的特点进行相应改进，其计算公式如式(10)所示。

(10)

假设最大惯性权重wmax=1、最小惯性权重wmin=0.3、最大迭代步数Tmax=100、s=-0.7，则四种惯性权重变化曲线如图2所示。

图2 惯性权重变化曲线

从图2比较可知，w1呈线性变化，在前期全局搜索能力较强，但如果搜索不到最优点，随着w的减小，局部搜索能力随之加强，容易陷入局部极值；w2在前期下降缓慢，有较强的全局搜索能力，但在后期下降很快，局部搜索能力较差；w3整个曲线下降缓慢，有较强的全局与局部搜索能力，但收敛速度较慢；而w4的变化曲线在前期和后期变化缓慢，中间区域下降较快，因此，前期能够保持较长时间的全局搜索能力以搜索到最优解区域，后期保持较长时间的局部开发能力搜索到最优解，并且收敛速度快。

1.3 IIWPSO-PNN训练过程

本文采用概率神经网络的识别率作为改进粒子群算法的适应度函数，由式(11)计算:

(11)

IIWPSO-PNN的训练步骤如下。

①载入训练样本与测试样本。

②初始化粒子群参数。

③用训练样本训练PNN网络，计算每个微粒的适应度函数值。

④将每个微粒的适应值pid与当前全局最优适应值pgd比较，更新pgd，使pgd保持较大值。

⑤根据式(5)和式(6)更新微粒的速度和位置，并根据式(10)更新惯性权重。

⑥终止条件。当训练样本识别率大于99%或者达到最大迭代步数，循环结束，否则返回步骤③。

⑦返回粒子群全局最优值pgd。

⑧用测试样本训练PNN网络，此时平滑参数为pgd，统计识别率，仿真结束。

2 仿真分析

本文以TE过程为试验背景，对IIWPSO-PNN网络仿真验证。TE过程是Downs和Vogel于1993年在“Computer & Chemical Engineer”上发表的一个典型化工过程[13]。其工艺流程图及详细仿真过程见文献[14]。

为保证仿真结果的客观性，所有仿真都在同一台计算机上完成，计算机处理器为Pentium(R) Dual-Core，安装内存(RAM)为2 GB，系统类型为32位操作系统；MATLAB版本为R2012b。

2.1 仿真验证

在仿真过程中，每一种故障的训练集数据是480组(都是有故障的情况)，测试集数据为320组(前160组为正常情况，后160组为有故障情况)。对于PNN网络，仿真中网络判断当前输入状况为正常情况，则输出1；反之，若判断当前输入状况为故障情况，则输出2。本文采用粒子群算法优化平滑参数，因此设置粒子的维数为1。根据文献[15],设置粒子数为10、最大迭代步数为100、wmax=1、wmin=0.3、c1=c2=2、粒子最大速度为1、r1和r2为[0,1]之间的随机数。

2.2 结果分析

将前人提出[10-12]的w1、w2和w3应用于PSO-PNN中，分别记为PSO-PNN1、PSO-PNN2和PSO-PNN3。为验证IIWPSO-PNN算法的有效性，将仿真结果与PNN、PSO-PNN1、PSO-PNN2和PSO-PNN3进行比较。其中概率神经网络的平滑参数σ设为0.7。本文给出TE过程中21种故障(共21种)的识别率，具体如表1所示。

表1 故障识别率比较

从表1可得，IIWPSO-PNN对每一种故障的识别率都在0.7以上，并且故障6、7的识别率达到了100%。故障3、11、15、16的识别率高于PSO-PNN1和PSO-PNN2；故障3、11的识别率高于PSO-PNN3，其他故障识别率基本一样；说明在故障3、11、15、16中，四种粒子群算法寻找到的平滑参数不一样，IIWPSO算法找到相对更优的平滑参数，因此故障诊断的效果更好。另外，经过粒子群优化的概率神经网络对于每一种故障的仿真结果都优于PNN(σ=0.7)网络。

故障3、11、15、16的收敛曲线如图3所示。

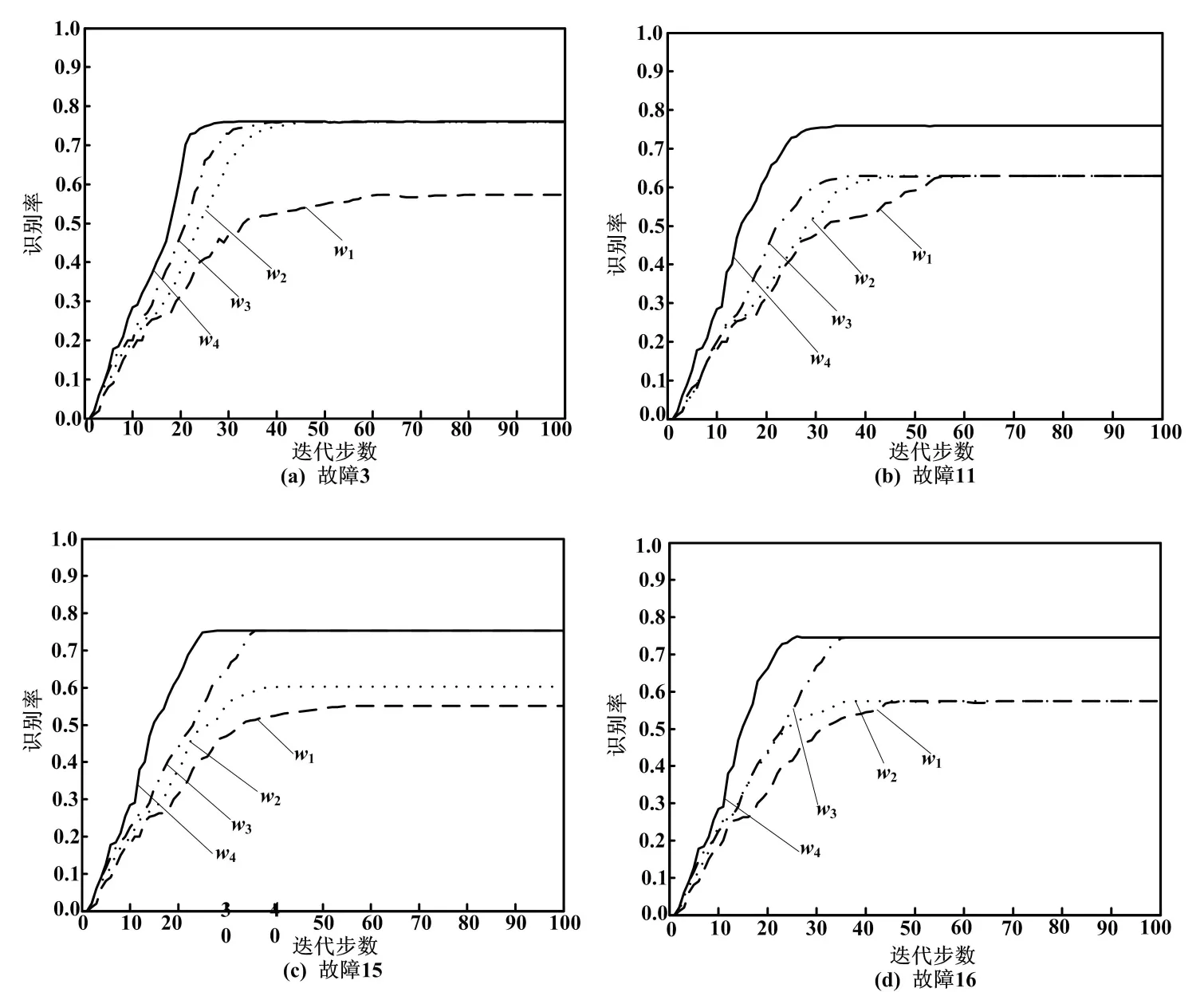
图3 收敛曲线

IIWPSO-PNN网络分别在20步、27步、25步开始收敛，并趋于稳定。比较发现，IIWPSO-PNN的收敛速度最快，其次是PSO-PNN3，且收敛速度优于PSO-PNN2，最慢的是PSO-PNN1。综上可知，针对故障3、11、15、16，IIWPSO-PNN网络不仅识别率高于其他网络，而且收敛速度更快，验证了改进算法的有效性。

3 结束语

本文以典型田纳西-伊斯曼化工过程为研究对象，针对过程数据分布复杂、高维以及相关等特性，采用概率神经网络进行故障诊断。针对网络中平滑参数的不确定性，提出改进粒子群优化算法寻找最优平滑参数的方法，并将其成功应用于概率神经网络中。TE过程仿真结果表明，针对故障1～21，IIWPSO-PNN的平均识别率是86.61%，与PNN、PSO-PNN1、PSO-PNN2和PSO-PNN3网络相比，平均识别率分别提高了21.91%、3.28%、2.15%和0.67%，收敛速度也相对加快。因此，收敛速度与识别率两方面数据表明，IIWPSO-PNN能有效解决化工过程故障诊断问题。

[1] WANG C Q,ZHOU J Z,QIN H,et al.Fault diagnosis based on pulse coupled neural network and probability neural network [J].Expert Systems with Applications,2011,38(6):14307-14313.

[2] YI J H,WANG J,WANG G G.Improved probabilistic neural networks with self-adaptive strategies for transformer fault diagnosis problem[J].Advances in Mechanical Engineering,2016,8(1):1-13.

[3] 黎群辉,张航.基于改进概率神经网络的交通标志图像识别方法[J].系统工程,2006,24(4):97-101.

[4] PORWIK P,DOROZ R,ORCZYK T.Signatures verification based on PNN classifier optimized by PSO algorithm [J].Pattern Recognition,2016,60(9):998-1014.

[5] 李浩,王福忠,王锐.免疫粒子群优化RBF神经网络的变压器故障诊断[J].自动化仪表,2016,37(11):4-7.

[6] SPECHT D.Probabilistic neural network [J] .Neural Networks,1990,3(1):109-118.

[7] KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks,1995:1942-1948.

[8] SHI Y,EBERHART R.A modified particle swarm optimizer[C]//Proceedings of the 1998 IEEE International Conference on Evolutionary Computation,1998:1942-1948.

[9] EBERHART R,SHI Y.Comparsion between genetic algorithm and particle swarm optimization[M]//Lecture Notes in Computer Science(Evolutionary Progranllning Vll).Berlin:Springer Press,1998:611-616.

[10]LEI K,QIU Y,HE Y.A new adaptive well- chosen inertia weights in particle automat- ically harmonize global and local search ability in particle swarm optimization[C]//ISSCAA,2006.

[11]胡建秀,曾建潮.微粒群算法中惯性权重的调整策略[J].计算机工程,2007,33(11):193-195.

[12]TICKABADI A,EBADZADEH M M,SAFABAKHSH R.A novel particle swarm optimization algorithm with adaptive inertia weight[J].Applied Soft Computing,2011(11):3658- 3670.

[13]DOWNS J J,VOGEL E F.A plant-wide industrial-process control problem [J].Computer & Chemical Engineering,1993,17(3):245-255.

[14]蒋浩天,拉塞尔，布拉茨.工业系统的故障检测与诊断[M].段建明,译.北京:机械工业出版社,2003.

[15]王东风,孟丽.粒子群优化算法的性能分析和参数选择[J].自动化学报,2016,42(10):1552- 1561.

ApplicationofIIWPSO-PNNinFaultDiagnosisofChemicalProcess

TAN Li，YU Chunmei

(School of Information Engineering,Southwest University of Science and Technology,Mianyang 621010,China)

Probabilistic neural network has been successfully applied in fault diagnosis of chemical process.In probabilistic neural network,the smoothing parameter has great influence on its performance and it is difficult to determine the optimal value.Therefore,the particle swarm optimization (PSO) algorithm is used to seek for the optimal smoothing parameter.In PSO algorithm,the inertia weight of linear variation is easy to make the algorithm fall into local extremum,so the inertia weight of nonlinear change is used to replace the inertia weight of linear change and apply into the improved inertia weight particle swarm optimization algorithm (IIWPSO).Then,the IIWPSO is applied to probabilistic neural network,which can automatically search and find the optimal smoothing parameter to be used for training and testing the probabilistic neural network.Compared with the inertia weight of the linear change and two kinds of nonlinear inertia weight (namedw1,w2andw3),thew1,w2andw3are applied to PSO-PNN respectively,which are denoted as PSO-PNN1,PSO-PNN2 and PSO-PNN3.Finally,the IIWPSO-PNN network is applied in Tennessee Eastman process,and compared with PNN,PSO-PNN,PSO-PNN1,PSO-PNN2 and PSO-PNN3 networks.The test results indicate that IIWPSO-PNN network has higher recognition rate and convergence rate when addressing the fault diagnosis problem.The feasibility and effectiveness of the IIWPSO-PNN algorithm in chemical process are verified.

Probabilistic neural network; Fault diagnosis; Smoothing parameter; Inertia weight; Particle swarm optimization; Tennessee-Eastman; Chemical process

TH165; TP277

： A

10.16086/j.cnki.issn1000-0380.201709003

修改稿收到日期:2017-03-19

四川省重点实验室开放基金资助项目(13zxtk16)、 西南科技大学博士基金资助项目(11zx07)

谭莉(1991—)，女，在读硕士研究生，主要从事故障检测与诊断方向的研究。E-mail：tanlicq521@163.com。 于春梅(通信作者)，女，博士，教授，主要从事故障诊断、模式识别、机器人控制方向的研究。E-mail：512232478@qq.com。