耦合量前馈的并网逆变器解耦控制
2017-09-25施火泉
魏 超,施火泉,张 敢
(江南大学物联网工程学院,江苏 无锡 214122)
耦合量前馈的并网逆变器解耦控制
魏 超,施火泉,张 敢
(江南大学物联网工程学院,江苏 无锡 214122)
传统的基于同步旋转坐标系的LCL型并网逆变器电流双闭环控制策略,在建立逆变器模型时,直接忽略了d轴和q轴之间的耦合关系。这样会造成系统模型的不准确,影响控制效果,为此提出了一种基于耦合量前馈的解耦策略。在各轴加入其他轴的耦合分量,耦合分量的大小和本轴被控对象实际产生的耦合量大小相等、方向相反。通过这种耦合量前馈补偿的策略最终消除了d、q轴之间的耦合关系,提高了系统控制模型和控制性能的精确性。为了进一步提高系统的控制性能,提出了一种基于频率特性的新型控制器参数设计方法。该方法可以准确计算出内外环控制器的参数,解决了传统控制器参数设计过程中需要反复试凑的问题。MATLAB仿真结果表明,所提出的控制策略取得了良好的解耦效果,并网电流的总谐波失真较小,实现了高功率因素并网。
LCL型逆变系统; 控制器; 耦合量; 前馈解耦; 电流双闭环; 数学模型; 频率特性
0 引言
利用太阳能、风能等新能源进行并网发电时,通常需利用并网逆变器将这些新能源得到的直流电转化为交流电[1-3],并采用LCL型滤波器滤除逆变器输出交流电中含有的高频谐波分量。为了满足并网需要,对LCL型三相逆变系统进行控制。基于dq旋转坐标系的LCL型三相逆变系统控制模型只需采用PI控制器,便可实现并网电流的无净差控制,且PI控制器的参数设计简单[4]。但在同步旋转坐标系下,控制模型的d、q轴之间存在耦合关系。传统的控制模型直接忽略这些耦合项,这样会造成系统模型的不准确,影响控制效果。
本文首先提出了一种前馈解耦策略,通过相应耦合量的前馈补偿,消除d、q轴之间的耦合关系。然后提出了一种并网电流和电容电流反馈的电流双闭环控制策略。通过电容电流内环增加系统阻尼,抑制系统谐振,再利用并网电流外环实现并网电流高功率因素并网。最后提出一种基于频率特性的新型控制器参数设计方法。该方法解决了传统设计方法中需要反复试凑的问题。仿真结果表明,在该控制策略下,d、q轴之间实现了完全解耦,系统的动态性能优良,满足了系统高功率因数并网的要求。
1 LCL型三相逆变系统的数学模型
LCL型三相并网逆变系统结构如图1所示。

图1 系统结构图
图1中:Udc、Idc分别为直流侧电压和电流;L1、L2分别为逆变器侧和网侧电感;Cf为滤波电容;Ua、Ub、Uc为三相逆变桥的输出电压;Ea、Eb、Ec为a、b、c相的电网电压;i1a、i1b、i1c分别为a、b、c相逆变器侧电流;i2a、i2b、i2c分别为a、b、c相的网侧电流;iCa、iCb、iCc分别为a、b、c相滤波电容电流[5-6]。
根据图1可以得到LCL型三相并网逆变系统在静止坐标系下的数学模型,即:

(1)
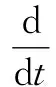
(2)
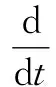
(3)
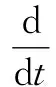
(4)
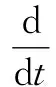
(5)
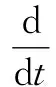
(6)
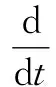
(7)

(8)

(9)
将式(1)~式(9)经Clark、park和拉氏变换后,可得:

(10)

(11)

(12)

(13)
根据式(10)~式(13)可得LCL型三相逆变系统在dq坐标系下的系统模型,其框图如图2所示。

图2 系统模型框图
从图2可知,在dq坐标系下LCL型三相逆变系统中逆变器侧电感L1和网侧电感L2的电流以及滤波电容C的电压之间存在耦合关系。
2 LCL型三相逆变系统解耦分析
为了获得精确的系统模型,需要对这些耦合项进行解耦设计。d轴解耦过程如图3所示。

图3 d轴解耦过程图
解耦设计的基本思想是在各轴加入其他轴的解耦分量,解耦分量的大小和本轴被控对象实际产生的耦合量大小相等、方向相反[7-8]。以d轴为例,则电感L1、电容C、电感L2的解耦系数分别为:
KdL1=ωL1i1q
(14)
Kdc=sL1ωCUcq
(15)
KdL2=s2CL1ωL2i2q-Ucd
(16)
3 控制策略的提出和控制器参数设计
为了实现对逆变系统的控制,采用电流双闭环控制策略[9-10]。图4为该电流双闭环控制中d轴的控制框图。

图4 d轴控制框图
在该双闭环控制系统中,外环采用并网电流i2d反馈,A1为并网电流反馈系数。内环采用电容电流i1d反馈,A2为电容电流反馈系数。kPWM为逆变桥等效比例环节;Gpi为并网电流控制器,本文选用 PI 调节器,Gpi=kp+ki/s。Gp为电容电流控制器,文中采用比例控制器,Gp=k。由于d轴与q轴具有对称性,下面以d轴为例设计控制器参数。根据图4,可以求出系统的开环传递函数为:
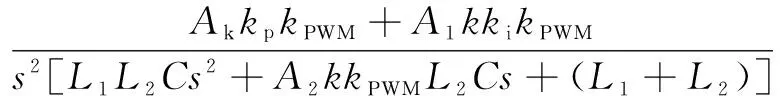
(17)
系统的闭环传递函数为:

(18)
式中:a4=L1L2C;a3=A2kkPWML2C;a2=L1+L2;a1=A1kkpkPWM;a0=A1kkikPWM;b1=kkpkPWM;b0=kkikPWM。
由劳斯判据可知,使系统稳定的条件为:
(19)
在设计控制器参数时,只要满足式(19)就能够保证系统的稳定性。将系统的开环传递函数转化成典型环节的形式:

(20)
其中:
(21)
基于期望对数频率特性的控制器设计方法为:低频段应具有较高的分贝数以保证系统的稳态精度,故校正后系统对数频率特性在低频段的斜率为-40 dB/dec。中频段特性曲线的斜率应为-20 dB/dec以使系统的稳定裕度和平稳性符合要求,中频段宽度h也需合理选取。为了满足系统响应快速性的要求,特性曲线的截止频率ωc应尽可能高。
系统期望与频率特性曲线如图5所示。

图5 系统期望与频率特性曲线图

4 仿真分析
为了验证所提出的基于耦合量前馈解耦的电流双闭环控制策略的性能,在MATLAB中搭建了相应的仿真模型。
直流侧的母线电压为400 V,逆变器侧电感L1=1.5 mH、网侧电感L2=1 mH,电容C=20 μF。内外环控制器的参数为:kp=0.194、ki=0.283、k=257.73,内外环反馈系数A1=A2=1。图6为A相的并网电压和电流波形。从图6可知,并网电压和电流相位几乎同相,实现了高功率因数并网。

图6 A相并网电压和电流波形图
当t=0.04 s时,系统从半载变化到满载和从满载变化到半载时,并网电压和电流的变化情况如图7所示。在两种情况下,并网电压大小保持不变,并网电流在半个周期内即可恢复,且并网电压和电流的相位始终保持一致。在该控制策略下,系统具有良好的动态性能。

图7 负载突变时并网电压和电流波形图
系统由半载到满载和由满载到半载变化时,d、q轴电流的变化情况如图8所示。d轴电流随负载变动发生相应改变,而q轴电流始终为0。可见在该解耦控制策略下,系统实现了有功功率和无功功率的完全解耦,即d、q两轴之间的解耦。
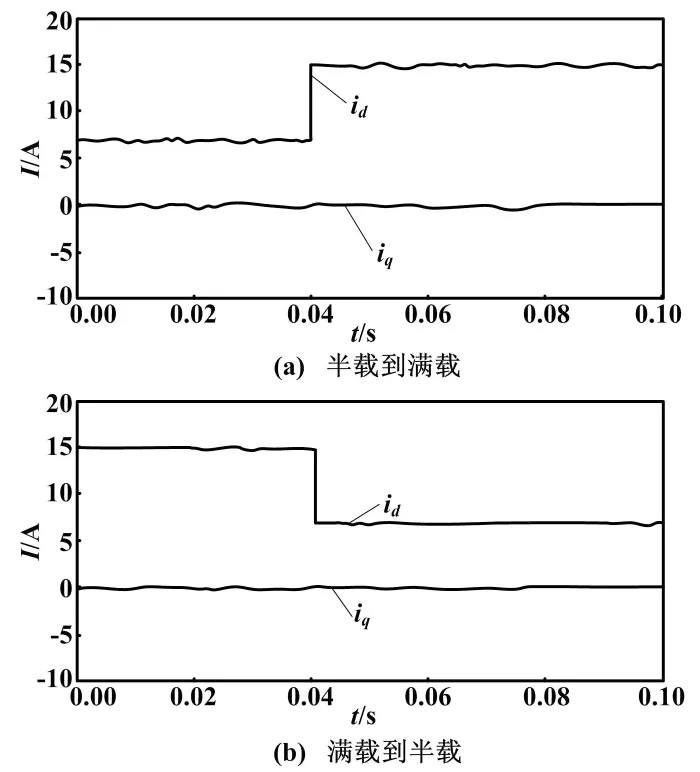
图8 负载突变时d、q轴的电流变化图
5 结束语
针对LCL型三相逆变系统在dq坐标系下的耦合问题,提出了一种耦合量前馈解耦的策略,建立了精确的系统模型。分析了解耦后的系统模型,结合并网要求提出了电流双闭环的控制策略。仿真试验表明,该解耦控制策略实现了高功率因数并网,系统动态性能良好,满足并网的各项指标要求。
[1] 阮新波,王学华.LCL型并网逆变器的控制技术[M].北京:科学出版社,2015.
[2] 许津铭,谢少军,张斌锋.分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J].中国电机工程学报,2015,35(16):4153-4166.
[3] 谢少军,许津铭.LCL滤波并网逆变器的电流控制技术研究综述[J].电源学报,2012,16(4):1-6.
[4] 毛艳芳,熊旋,陈旭,等.单相逆变器双环控制改进策略研究[J].电测与仪表,2014,51(8):69-74.
[5] 胡雪峰,韦徵,陈轶涵,等.LCL滤波并网逆变器的控制策略[J].中国电机工程学报,2012,32(27):142-148.
[6] 朱海洋.独立光伏发电系统逆变器的设计与仿真[J].自动化仪表,2014,35(4):23-25.
[7] 包献文,卓放,谭佩喧.三相LCL型并网逆变器的模型分析及解耦控制[J].西安交通大学学报,2014,48(2):44-49.
[8] 屈克庆,李文旗,叶天凯,等.基于状态反馈的LCL型逆变器解耦控制策略[J].电工技术学报,2016,31(20):130-138.
[9] 易桂平,黄慧春,胡仁杰.基于LCL输出滤波器的双环控制并网逆变器研究[J].太阳能学报,2016,37(1):40-46.
[10]刘文军,周龙,陈剑,等.LCL并网逆变器的电流双闭环控制[J].电力系统保护与控制,2016,44(17):52-57.
[11]王百永,张俊伟,郑华荣,等.LCL型并网滤波器参数设计方法[J].电源学报,2012,12(6):116-122.
DecouplingControlBasedonCouplingFeedforwardforGridConnectedInverter
WEI Chao,SHI Huoquan,ZHANG Gan
(College of Internet of Things,JiangNan University,Wuxi 214122,China)
For LCL grid connected inverter,in traditional current double closed loop control strategy based on synchronous rotating coordinate system,the coupling betweendaxis andqaxis is ignored when the inverter model is established.This will cause the system model being inaccurate,and influence the control effects.Thus,a decoupling control strategy based on feedforward coupling is proposed.The coupling components are added in other axes,the amount of coupling component is equal to the actual coupling component of the controlled object,while the direction is reverse.By this coupling feedforward compensation strategy,the coupling relation betweendandqaxis is eliminated,so the precision and performance of the system control model are improved.In order to further improve the control performance of the system,a new design method for parameters of controller based on frequency characteristics is put forward.The method can accurately calculate the parameters of the inner and outer loop controllers,and avoid the trouble of repeated process of test and try in traditional design method for controller.The simulation results in MATLAB show that the proposed control strategy reaches good decoupling effect,and the total harmonic distortion (THD) of grid connected current is smaller,and the grid connected with high power factor can be implemented.
LCL type inverter system; Controller; Coupling quantity; Feedforward decoupling; Current double closed loop; Mathematical model; Frequency characteristic
TH86;TP214+.5
: A
10.16086/j.cnki.issn1000-0380.201709005
修改稿收到日期:2017-04-14
魏超(1992—),男,在读硕士研究生,主要从事光伏系统并网发电技术的研究。E-mail:601930172@qq.com。 施火泉(通信作者),男,学士,高级工程师,主要从事电力电子与电力传动、用电信息采集方向的研究。 E-mail:1185114075@qq.com。
