基于滤波器的桥式起重机无源滑模防摆控制研究

陈志梅，高武龙，张井岗

(太原科技大学电子信息工程学院，山西 太原 030024)

基于滤波器的桥式起重机无源滑模防摆控制研究

陈志梅，高武龙，张井岗

(太原科技大学电子信息工程学院，山西 太原 030024)

桥式起重机防摆控制系统具有高度非线性、欠驱动特性，定位和摆角相互影响，绳长和负载质量经常变化，且存在空气阻尼和摩擦等不确定性因素，因此，常规的线性防摆控制方法往往防摆效果不理想。针对上述问题，在考虑负载的提升过程及绳长的变化前提下，建立了欧拉-拉格朗日三维误差系统；通过对系统进行无源性分析，结合无源控制和滑模控制各自的优点，设计了基于滤波器的无源滑模控制器，构造了Lyapunov能量函数且证明了其稳定性。防摆控制系统结构简单，不但消除了滑模控制高频抖振现象，使得系统渐近稳定，而且有效地实现了小车的快速定位和负载的有效防摆，提高了系统的鲁棒性，改善了系统的控制性能。仿真结果验证了控制方案的正确性和有效性。

无源控制； 滑模控制； 反馈补偿； Lyapunov能量函数； PID； 桥式起重机； 欠驱动系统； 滤波器

0 引言

桥式起重机在工作时，由于小车加减速和负载提升的惯性，以及风力、摩擦等因素的影响，会引起负载的摆动，导致作业效率降低，甚至引发安全事故。因此，桥式起重机防摆控制成为近年来的研究热点[1-10]。桥式起重机具有高度非线性、欠驱动特性，受定位和摆角相互影响，绳长和负载质量经常变化，存在空气阻尼和摩擦等不确定因素，因此，常规的线性防摆控制方法往往难以奏效。刘德君[3]等针对吊车系统设计了非线性PID控制器，系统获得了更好的性能，但难以实现参数的实时调整。孙宁[4]等借助非线性耦合规划了小车的运行轨迹，改善了控制系统的性能，然而对于复杂的工作环境，离线规划的轨迹常常不准确，且对外界干扰的鲁棒性较差。刘殿通[5]等采用滑模控制，通过设计分层滑模面将系统分解成定位子系统和防摆子系统，对外界干扰和系统参数摄动具有完全自适应性，但出现了抖振现象。贾鹏霄[6]等将比例微分(proportion derivative,PD)自适应控制与输入整形相结合，并将其应用于桥式起重机的防摆控制中，但只考虑了二维模型并进行了线性化。方勇纯[7]等从能量入手，基于无源控制的方法设计了两种非线性控制器，实现了系统状态的渐近镇定。该方法能够简化控制器的设计，不过该模型较简单，未考虑绳长变化等因素。董明晓[8]等人将优化思想引入到滑模控制器设计中，设计了一种时滞滤波器。王晓军[9]等人设计了一种最优随机时滞滤波器。该滤波器具有多峰极、对参数变化不灵敏以及设计简单的特点，能够提高对绳长变化、频率变化和阻尼误差的强鲁棒性。

本文针对桥式起重机三维模型，考虑负载绳长的变化，结合无源控制和滑模控制各自的优点，设计了无源滑模控制器，并进行滤波，有效地抑制负载的残余振荡，消除滑模控制高频抖振现象，进一步提高系统的鲁棒性。该系统结构简单，能有效实现负载的防摆和小车精确定位。

1 系统动力学模型

三维桥式起重机系统模型如图1所示。图1中：M、m分别为小车和负载的质量；l为绳长；θx为绳子在XZ平面上的投影与Z轴的夹角，θy为绳子在XZ平面上的投影与绳子本身的夹角；fx和fy分别为X、Y轴的水平驱动力，fl为沿绳子方向的提升驱动力。

利用欧拉-拉格朗日方程建立动力学模型，不考虑绳子质量以及其他因素影响，得到的桥式起重机三维动力学模型如式(1)所示[11]。

(1)

将该三维模型改写成如式(2)的矩阵形式:

(2)

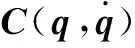
状态向量如式(3)所示：

q=(x,y,l,θx,θy)T

(3)

惯性矩阵如式(4)所示：

(4)

(5)

式(5)中，a、b、c的表达式如下：

重力向量如式(6)所示：

G(q)=(0,0,-mgcosθxcosθy,mglsinθxcosθy,mglcosθxsinθy)T

(6)

控制输入向量如式(7)所示：

τ=(fx,fy,fl,0,0)T

(7)

取小车位置平面为零势能参考点，则势能为：

P=-mglcosθxcosθy

(8)

2 无源性分析

对于桥式起重机系统(2)，其能量为:

(9)

对上式求导，可得：

由此可知，桥式起重机系统(2)对于输入τ和输出q具有无源性。

3 基于滤波器的无源滑模控制

3.1 无源控制

本文的控制目标是对任意的初始状态(xy,y0，l0,θx0,θy0)T,考虑负载的提升过程，在吊绳变化的情况下，能快速到达终点位置(0,0,ld，0,0)T，保证小车的精确定位和负载的消摆。为了实现这一目标，对系统(2)施加控制输入，如式(10)所示：

(10)

式中：qd=(xd,yd,ld,θxd,θyd)T为系统期望状态值，一般θxd=θyd=0。

(11)

式中：u为无源控制。

(12)

对式(12)求导，得：

(13)

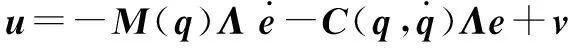
(14)

式中：Λ=diag(λ1,λ2,λ3,0,0),λi>0,i=1,2,3。

假设闭环系统的能量为：

(15)

(16)

以上求导表明：误差闭环系统也具有无源性。

3.2 滑模控制

(17)

则：

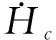
(18)

为保证能量函数衰减性，滑模控制采用常值切换控制，即：

v=-v0sgn(s)v0>0

(19)

则系统的无源滑模控制律(passive-based control sliding mode controller,PBC-SMC)为：

(20)

为了消除抖振，采用饱和函数代替符号函数，令v=-v0sat(s) ，则控制律为：

(21)

如果v=0、s=0，则可推出：

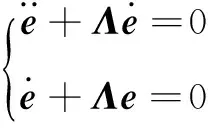
(22)

由式(20)可知，t→∞、e(t)→0，则闭环系统为零状态可测系统。根据LaSalle不变集定理[12]可知，系统的零平衡状态渐近稳定；又因为系统具有零状态可检测和无源性，根据Lyapunov稳定定理可知，闭环系统也是稳定的。

3.3 基于滤波器的无源滑模控制

为了抑制负载的残余振荡，将一个低通滤波器加到无源滑模控制器的输出端，对控制信号进行滤波；再利用基于反馈补偿的误差闭环系统的无源性和稳定性，构造一个基于滤波器的控制系统。系统结构图如图2所示。

图2 系统结构图

设计的滤波器为低通滤波器，其传递函数为：

(23)

使得系统等效输入δ满足：

(24)

选择新的滑模面为：

(25)

选取闭环系统的控制Lyapunov函数同式(17)所示。

对Hc求导，得：

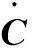
(26)

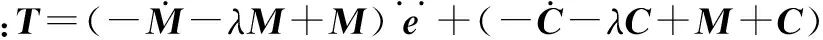
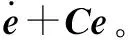
为保证能量函数的衰减性，令：

λu+T=-λβsat(s)

(27)

则系统应满足：

(28)

式中：α=diag(α1,…,αi)。

4 仿真研究

设系统参数：M=2 kg，m=1 kg，初始值(x0,y0,l0,θx0,θy0)=(-5,-5,5,0,0)，期望值(xd,yd,ld,θxd,θyd)= (0,0,2.5,0,0)。取控制器参数：v0=5,λ1=3.5,λ2=1,λ3=4,α=diag(0.8,2.5,4)。对桥式起重机防摆控制系统进行仿真研究，得到的绳长变化曲线、小车位移曲线及摆角变化曲线如图3～图5所示。

从图3～图5可以看出，两个控制器均在20 s时到达期望的位置，小车位置和绳长定位准确。在此过程中，相比PBC-SMC控制器，PBC-SMC-滤波器控制器于5 s内完成提升动作，时间缩短了3 s；小车位移系统收敛速度也更快，负载摆动的幅度更小，未出现残余振荡。

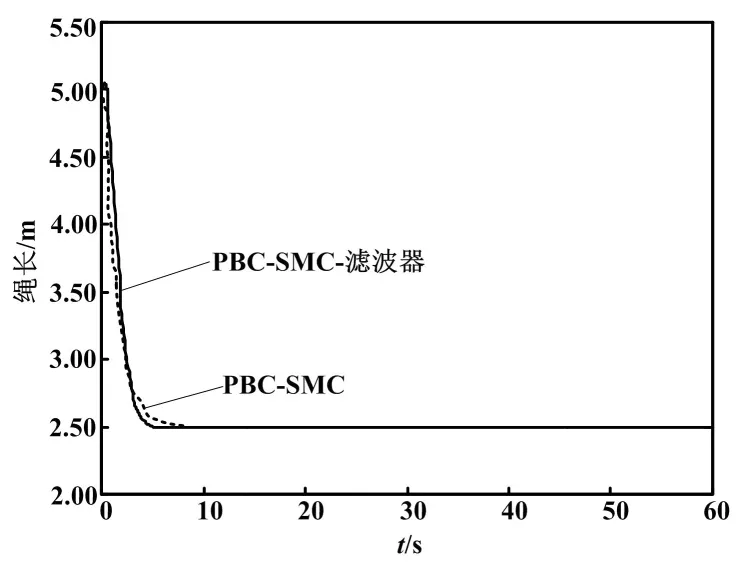
图3 无干扰绳长变化曲线

图4 无干扰小车位移曲线

在t=20 s时，在基于滤波器的无源滑模控制系统中加入单位阶跃干扰后，摆角变化曲线如图6所示。

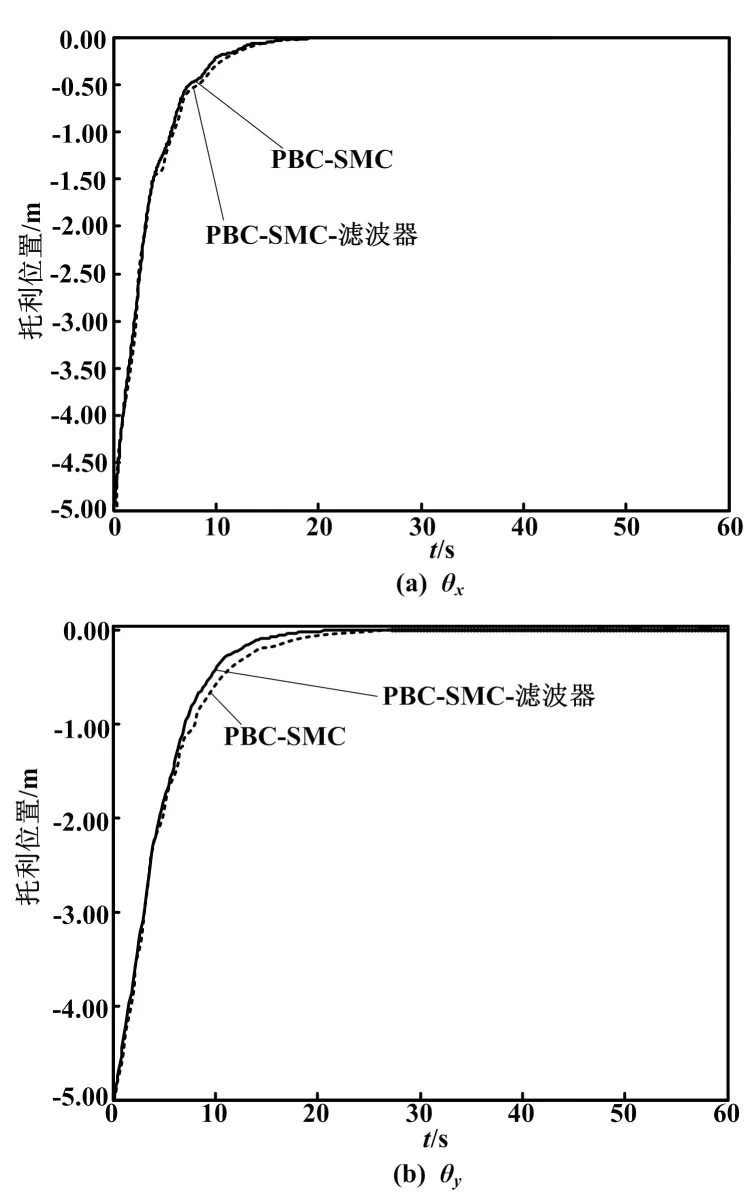
图5 无干扰摆角变化曲线

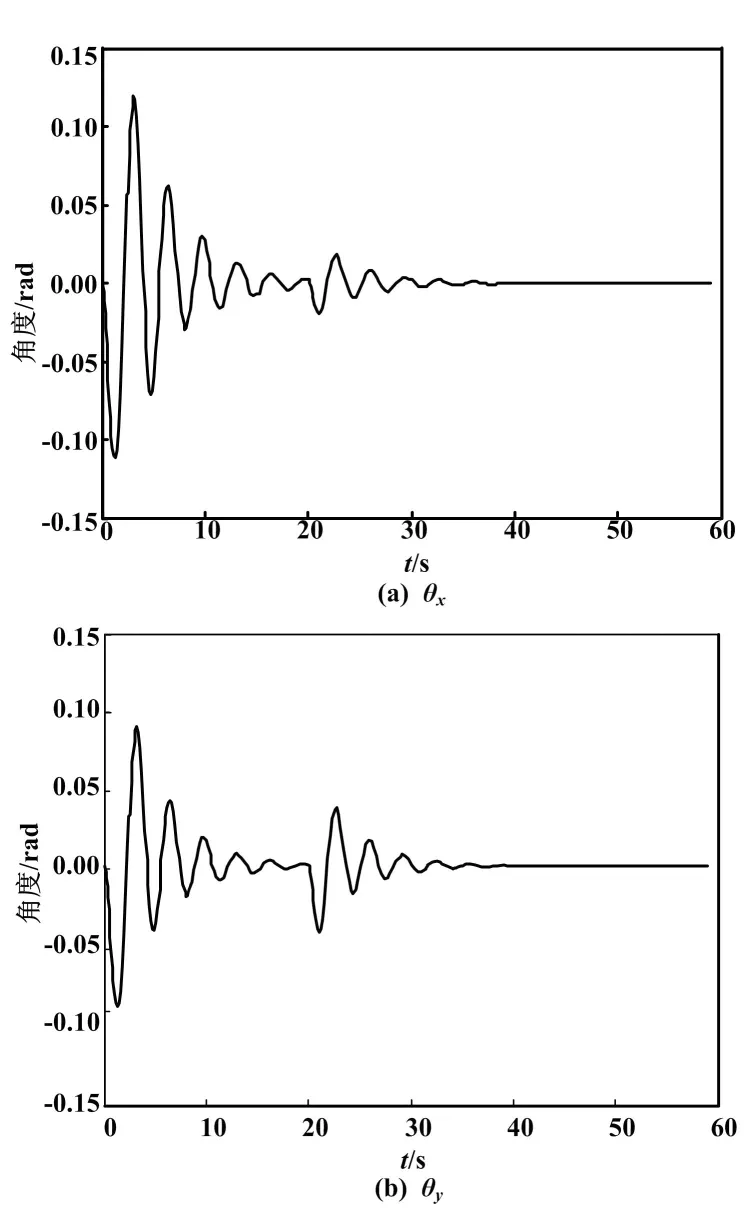
图6 单位阶跃干扰下摆角变化曲线

由图6可知，系统在外界干扰下，X、Y轴两个摆角经过小幅的振荡后，最终趋于稳定，可见系统有较好的抗干扰能力和较强的鲁棒性。

5 结束语

本文在桥式起重机三维误差控制系统无源性分析的基础上，考虑负载绳长的变化，结合滑模控制理论，修改了系统的控制Lyapunov能量函数，研究了基于滤波器的桥式起重机无源滑模防摆控制方法。该方法实现了小车的精确定位和负载的有效防摆。仿真结果证明了该方法的正确性和有效性，为进一步的试验研究奠定基础。

[1] 杨斌,刘惠康.桥式起重机防摆控制器的设计[J].制造业自动化,2012,34(1)：122-124.

[2] 李众峰,徐为民,谭莹莹,等.欠驱动桥式吊车自适应PID控制[J].计算机测量与控制,2013,21(6):1522-1540.

[3] 刘德君,纪宏利,白晶.基于非线性PID的吊车防摆定位控制[J].微计机算信息，2007,25(11)：51-52,186.

[4] SUN N,FANG Y,MA B J.Motion planning for bridge cranes based on iterative strategy[C]//Proceedings of the Chinese Control Conference,2010:326-331.

[5] LIU D T,YI J Q,ZHAO D B,et al.Swing-free transporting of two dimensional bridge crane using sliding mode fuzzy control[C]//Proceedings of the 2004 American Control Conference,2004:1764-1769.

[6] 贾鹏霄,李恩,梁自泽,等.自适应控制结合输入整形抑制单模态弹性机构振动研究[J].振动与冲击,2013,32(17):189-193.

[7] FANG Y C,ZERGEROGLU E,DIXON W E,et al.Nonlinear coupling control laws for an bridge crane system [C]//Proceedings of the 2001 IEEE International Conference on Control Applications,2001:639-644.

[8] 董明晓,郑康平,张明勤.桥式起重机消摆控制仿真研究[J].系统仿真学报,2005(6):1459-1461.

[9] 王晓军,邵惠鹤.鲁棒最优随机时滞滤波器的频域设计方法[J].控制与决策,2006(10):1172-1176.

[10]MISRAN F,RAMLI M S.Experimental investigations of low pass filter techniques for sway control of a gantry crane system[C] //Proceedings of the International Conference on Electronic Computer Technology,2010:1-4.

[11]LEE H H.Modeling and control of a three-dimensional bridge crane [J].Measurement and Control,1998,120(4):471-476.

[12]王久和.无源控制理论及其应用[M].北京:电子工业出版社,2010:52-54.

ResearchonPassiveSlidingModeAnti-SwingControlBasedonFilterforBridgeCrane

CHEN Zhimei,GAO Wulong,ZHANG Jinggang

(School of Electronics and Information Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China)

The anti-swing control system of bridge crane has highly nonlinear and under-actuated characteristics, and the positioning and swing angle are mutually affected.The rope length and mass of load are changing frequently, and the air damping and friction factors are uncertain,so the conventional linear anti-swing control method is difficult to work effectively.For these problems,in consideration of the changes of load lifting and rope length,the Euler Lagrange three dimensional error system has been established,through analyzing the passivity of the system,and combining together the advantages of both passive control and sliding mode control,a passive sliding mode controller based on filter is designed,and the stability of system is proved by constructing the Lyapunov energy function.This anti-swing control system is in simple structure,and it not only eliminates the chattering of sliding mode control,to make the system asymptotically stable,but also effectively realize fast positioning of trolley and load anti-swing,thus the robustness and other performances of the system are improved.The simulation results verify the correctness and effectiveness of the control scheme proposed.

Passive control; Sliding mode control; Feedback compensation; Lyapunov function; PID; Bridge crane; Under-actuated system； Filter

TH39;TP273

： A

10.16086/j.cnki.issn1000-0380.201709002

修改稿收到日期:2016-12-09

山西省自然科学基金资助项目(2014011020-2)、山西省研究生教育改革研究基金资助项目(20142058)

陈志梅(1970—)，女，博士，教授，主要从事机电一体化系统控制等方向的研究。E-mail：zhimeichen400@163.com。