细长轴车削加工振动特性研究

孙 斌，沈 彤

(中船重工海博威(江苏)科技发展有限公司，江苏 扬州 225131)

细长轴车削加工振动特性研究

孙 斌，沈 彤

(中船重工海博威(江苏)科技发展有限公司，江苏 扬州 225131)

根据细长轴难加工性，提出一种双刀、拉夹顶尖的方式，建立了力学模型，得出了细长轴振动特性的固有频率理论计算公式，利用 Matlab 软件求出振型函数的振动方程曲线。 利用 ANSYS Workbench软件进行了模态分析，得出其前 4阶固有频率，为细长轴的实际加工提供了一定的理论依据。

细长轴；振动；模态分析；ANSYS Workbench

0 引 言

细长轴类零件(长径比大于20)在机械领域中有着极其广泛的应用，而在加工的过程中，细长轴是较难加工的一类零件，因为细长轴零件刚度低，在切削力作用下极易产生弯曲变形，导致工件振动加剧，造成工件尺寸偏差和加工表面质量差。为此，很多学者对细长轴的车削特性进行了研究。仲良等人提出了双刀车削细长轴的方式以此来减少振动，对其进行了理论分析和仿真，验证了双刀车削要优于单刀车削[1]。李康等人针对细长轴车削振动问题，提出了一种拉压顶尖的结构，变压力为拉伸力，降低了振动的可能性，针对让刀现象，研制了超声振动车削系统和自制跟刀架的组合结构，通过实验证明了用拉夹顶尖、超声振动车削方式和自制跟刀架的组合加工细长轴的有效性[2]。Clancy等人改进了切削加工的动态模型，研究了刀具磨损和加工中出现的阻尼对切削加工稳定性的影响[3]。Chiou等人研究了细长刀具磨损对工件进行车削加工时切削稳定性的影响[4]。

本文提出一种双刀、拉夹顶尖的方式来减少振动，从而获得较高精度的细长轴，从理论的角度对该方式进行理论分析和仿真分析。

1 切削过程中的动力学建模

细长轴是一类需求量大、广泛应用的零件，其缺点是长径比大，刚度不足，在车削加工过程中极易产生振动，从而导致其加工精度低。本文采用对称式双刀-拉夹顶尖模型，将Euler-Bernoulli梁作为力学模型[5-10]，如图1所示。

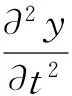
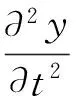
(1)

消去dx得：

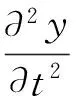
(2)

根据材料力学中平面假设和不考虑物体转动的惯性影响，则由力矩平衡方程可知：

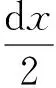
(3)

则有：

(4)

将其代入式(1)得：

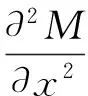
(5)

由材料力学知识中的弯曲变形中弯矩和挠度的关系有：

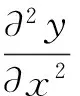
(6)

式中：E为细长轴的弹性模量；I为细长轴的横截面惯性矩。

将式(6)代入式(5)，并对x求偏导，得：

(7)

在式(7)中，令p(x,t)=0，m(x,t)=0，则得到细长轴的自由振动方程：

(8)

(9)

式(9)为4阶偏微分方程，采用分离变量将其转化成常微分方程，设方程的解为y(x,t)=ψ(x)q(t)，ψ(x)为振型函数，q(t)为时间函数。将其代入式(9)，得：

(10)

要使式(10)对任意的x和t都成立，则式(10)两端必须等于常数，设该常数为-ω2，则有：

(11)

(12)

式(11)通解为一简谐函数：

q(t)=C1sinωt+C2cosωt

(13)

式中：C1，C2为积分常数；ω为细长轴的振动固有频率。

式(12)通解为：

ψ(x)=D1coshβx+D2sinhβx+D3cosβx+D4sinβx

(14)

式中：β4=ω2/a2，D1，D2，D3，D4为积分常数。

由于细长轴在切削过程中，一端采用固定，一端采用拉夹顶尖，故在两端受到径向位移和转角位零，则边界条件转化为：

(15)

根据这4个边界条件，可以确定方程(14)的4个常数的比值关系，并确定细长轴的固有频率ω与振型函数ψ(x)。

2 细长轴的理论振型曲线

由细长轴振动力学模型的边界条件及式(14)可得出细长轴的特征方程为:

(cosβl-coshβl)2=sinh2βl-sin2βl

(16)

用数字解法可求出特征方程的前5 阶特征根为4.693 3，7.814 8，10.972 1，14.134 9。

各特征根近似为：

(17)

因此，细长轴的各阶固有频率为:

(18)

与ωi相对应的振型函数为：

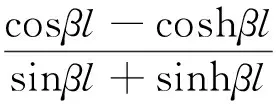
(19)

将βil的前3阶特征值代入式(19)，得到细长轴前3阶切削加工振型函数：

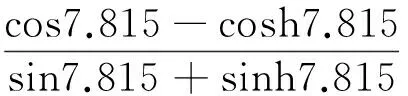
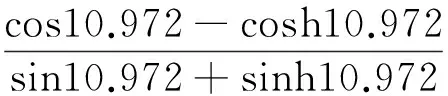
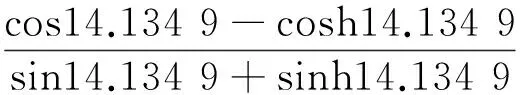
用 Matlab 数值分析软件，编程后得到振型函数的振动曲线，如图2所示。

3 细长轴的有限元分析

建立有限元模型时，细长轴材料为45钢，细长轴选用Solid 186单元，长度为1 m，直径为40 mm，弹性模量为208 GPa，泊松比为0.3，密度为 7.8 g/cm3，对细长轴左、右两端施加全约束。

振动模态是弹性结构固有的、整体的特性，通过模态分析可以搞清楚结构在某一易受影响的频率范围内的各阶主要模态的特性，本文利用ANSYS Workbench 17.0软件对细长轴进行模态分析，由于低阶的固有频率对细长轴的振动影响较大，因此对其进行模态分析时只拓展前4 阶模态，仿真模型如图3所示。

通过比较图2与图3，仿真振型图和理论振动方程曲线二者结果极为一致。由模态分析可得出细长轴车削过程的前 4阶固有频率分别为，f1=190.81 Hz，f2=520.26 Hz，f3=1 005.5 Hz，f4=1 633.4 Hz。而通过理论计算得出细长轴车削前 4 阶固有频率分别为f1=181.03 Hz，f2=502.18 Hz，f3=989.92 Hz，f4=1 642.9 Hz。两者结果接近，由此说明仿真分析和理论模型的正确性。

4 结束语

本文通过细长轴的振动理论，建立了细长轴双刀、拉夹顶尖方式的力学模型,并进行了有限元仿真分析，得出了细长轴前4阶固有频率，为细长轴的切削加工提供了一定的理论依据，在实际加工过程中应避开固有频率。本文未对双刀、拉夹顶尖的方式做进一步研究与实验，这是接下来研究的重点。

[1] 仲良，邓志平，尚广云，等．双刀车削细长轴振动特性分析[J]．中国工程机械学报，2015，13(5)：441-445．

[2] 李康，陈风，郭国强，等．带自制跟刀架的振动车削细长轴实验研究[J]．机械设计与制造，2015(6)：119-125．

[3] CLANCY B E ，SHIN Y C.A comprehensive chatter prediction model for face turning operation including tool wear effect[J]．International Journal of Machine Tools & Manufacture,2002，42(9)：1035-1044.

[4] CHIOU R Y ，LIANG S Y.Chatter stability of a slender cutting tool in turning with tool wear effect[J]．International Journal of Machine Tools & Manufacture,1998，38(4)：315-327.

[5] 邓志平，金龙，张洪.细长轴的双刀车削加工精度的研究 [J].中国工程机械学报，2014，12(1)：44-47.

[6] 金龙，邓志平，张洪，等.细长轴的车削仿真研究[J].西华大学学报，2014，33(3)：40-43.

[7] 韩荣第，郭建亮.细长杆车削系统的动力学建模[J].机械研究与应用，2004，17(3)：16-17.

[8] 李银玉，吴敬.超细长轴车削加工及夹具设计[J].机床与液压，2016，44(10)：187-188.

[9] 谢新伟，赵千红，徐国荣，等.减缓车削加工时细长轴振动的方法[J].应用能源技术，2007(9)：9-13.

[10] 张强，雷金果，黄昌华，等.细长轴切削过程的振动特性分析[J].煤矿机械，2014，35(1)：92-94.

ResearchintoVibrationCharacteristicofSlenderShaftinTuringProcess

SUN Bin,SHEN Tong

(CSIC Haibowei(Jiangsu)Technology Development Co.,Ltd，Yangzhou 225131，China)

Because the slender shaft is difficult to process,this paper puts forward a new method of double-pole and chuck-pulling clamper,establishes the mechanical model,and fetches the theoretical calculation formula of inherent frequency about the vibration characteristics of slender shaft,uses the Matlab software to obtain the vibration equation curve of vibration function,uses ANSYS Wokbench software to perform the modal analysis,and educes the first 4-step inherent frequencies,which provides a definite theoretical basis for the actual machining of slender shafts.

slender shaft;vibration;modal analysis;ANSYS Wokbench

TN05

：B

：CN32-1413(2017)04-0117-04

10.16426/j.cnki.jcdzdk.2017.04.029

2017-05-02