基于区域极点配置的静态输出反馈可靠控制

房志铭，姚 波*，王福忠

1.沈阳师范大学数学与系统科学学院，沈阳，110034； 2.沈阳工程学院基础部，沈阳，110036

基于区域极点配置的静态输出反馈可靠控制

房志铭1，姚 波1*，王福忠2

1.沈阳师范大学数学与系统科学学院，沈阳，110034； 2.沈阳工程学院基础部，沈阳，110036

对于包含不确定项的线性系统，提出了带有执行器故障的静态输出条形区域极点配置的反馈控制问题。首先给出在不考虑故障时设计控制器使系统极点位于所要求的条形区域内的充分条件；然后讨论对于同一系统同一控制器在考虑执行器故障时，不确定系统发生的不稳定状况；而后，对同一故障模型重新设计静态输出反馈控制器使系统在发生故障后极点仍然配置在所要求区域。通过数值仿真，验证了本文设计控制器方法的有效性。

区域极点配置；执行器故障；静态输出反馈；不确定系统；LMI

1 问题提出

通常，系统的极点均落在左半复平面上是定常线性系统保持稳定的充分必要条件。而针对定常线性离散系统，系统极点落在复平面上以原点为中心的单位圆内是其稳定的条件。另外，在实际生产生活中，一个系统除了要具有优秀的稳态特性外，还需具备优秀的瞬态特性，以保证实际系统的一些性能要求，如调整时间、超调量等。大多数情况下系统的瞬态特性和极点位置有关，因此极点配置问题一直是控制理论中重要的课题之一。对于极点配置问题，一些学者给出了方法[1-3]。

在实际的工业生产中，一些机械经常会出现各种各样的故障，尤其是执行器通道故障。因此，给系统设计一个控制器，使其在发生故障的情况下仍可以保持稳定并正常运行是有必要的。可靠控制是指一个系统无论发生故障与否，均可通过设计可靠控制器使其保持稳定运行，并达到一定的性能指标。20世纪70年代 Siljak提出可靠控制的概念，而后一些可靠控制器的设计方法被相继提出[4-6]。文献[7]提出了具有双故障的动态输出反馈可靠控制器的设计方法，文献[8]提出了针对时滞不确定线性系统静态输出反馈可靠控制器的设计方法，文献[9]讨论了一类非光滑不确定系统若干控制的问题，文献[10]给出了在极点配置基础上的不确定系统状态反馈设计方法。静态输出反馈控制器的设计问题一直是控制理论中的焦点之一，针对静态输出反馈控制问题，学者也提出了一系列方法。文献[11]和文献[12]均是研究静态输出反馈控制器的设计问题。以上的文献涉及到可靠控制和静态输出反馈问题。

本文前人研究的基础上，研究带有不确定项的系统中静态输出反馈可靠控制中的条形区域极点配置的问题，并利用LMI给出控制器的设计方法。本文设计的控制器能保证无论系统发生故障与否，均保持运行的稳定，并使系统的极点配置在所要求的条形区域内。最后应用Matlab软件仿真，确定本文结论的有效性。

2 问题描述

考虑带有不确定项的线性系统：

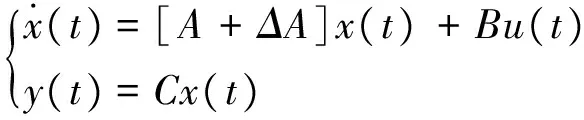
(1)

其中，x(t)∈Rn是状态标量，u(t)∈Rm是控制变量，y(t)∈Rp是输出变量，A、B是适维矩阵，C是适维行满秩矩阵，ΔA为不确定项且满足如下条件：ΔA=DH(t)E，式中，D、E为适维维数的常数矩阵；H(t)为未知的时变实值连续矩阵函数，其元素Lebegue可测，且：

HT(t)H(t)≤I

执行器连续增益故障矩阵模型为：

uf(t)=Fau(t)

(2)

其中，u(t)∈Rp为控制输入变量，uf(t)∈Rp为考虑执行器故障的输入变量。

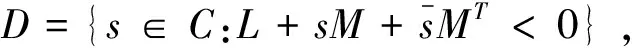
MDA,X<0

其中，MDA,X=L⊗X+M⊗AX+MT⊗AXT

引理2根据引理1，矩阵x(t)∈Rn的所有特征值均在h1和h2垂直条形区域的充分必要条件是存在对称正定矩阵A，使得

引理3在考虑执行器故障时，对单故障进行处理(凸组合法)，设：

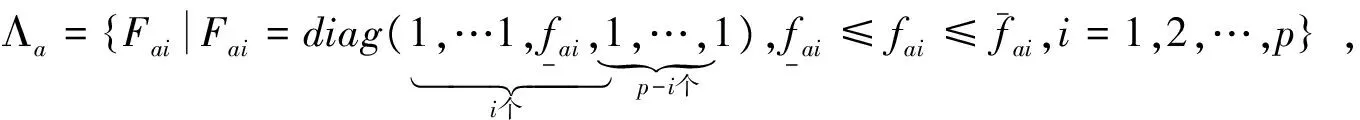
引理4设X和Y为适维定常矩阵，H为适维时变矩阵，且满足HTHI，那么对任意常数ε>0有

XHY+YTHTXT≤εXXT+ε-1YTY。

2 主要结果

2.1 无故障的条形区域极点配置静态输出反馈控制器设计

对系统(1)引入静态输出反馈控制器：

u(t)=Ky(t)

(3)

由此构成闭环系统：

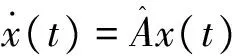
(4)

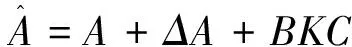
定理1对于系统(1)，如果存在标量ε>0,α>0及静态输出控制器(3)使得闭环系统(4)的极点配置在h1和h2之间的垂直条形区域的充分必要条件是存在对称正定矩阵X和矩阵K,U,V，使：

VC=CX

其中，Ω=AX+XAT+BUC+CTUTBT，那么存在静态输出反馈控制K=UV-1使得闭环系统(4)的极点配置在条形区域中。

证明根据引理1可知，使闭环系统(4)的极点配置在h1和h2之间的条形区域的充分必要条件是存在对称正定矩阵X使

(5)

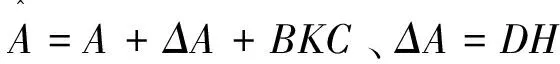
其中Π=DH(t)EX+(DH(t)EX)T。

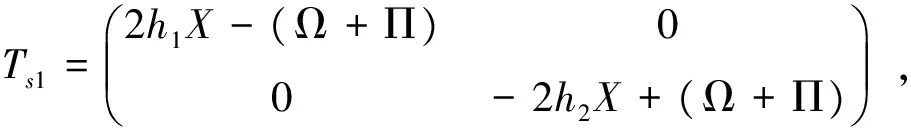
根据引理4可以得到：

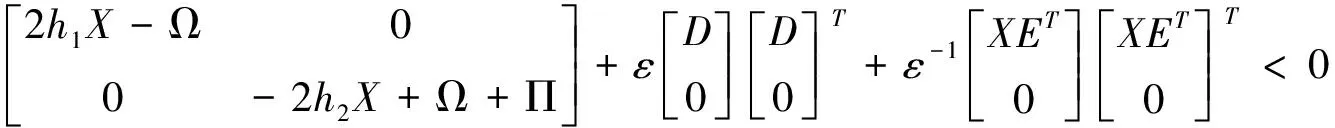
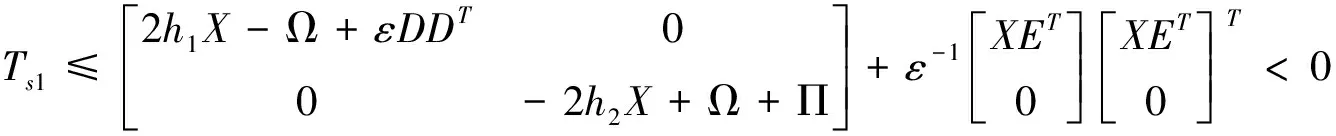
(6)

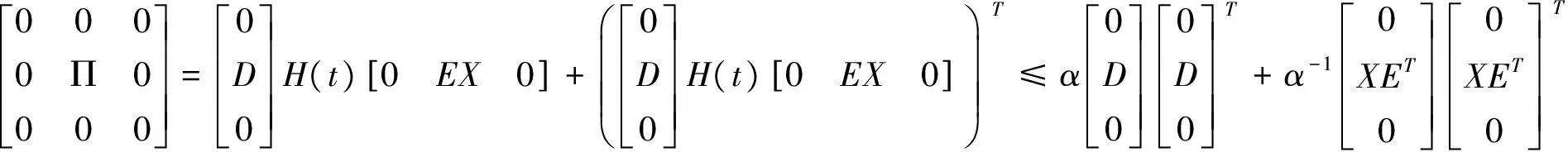
代入(6)有

根据Schur补引理整理，同时满足Ts1<0,定理得证。

2.2 基于执行器故障的条形区域极点配置静态输出反馈控制器设计

系统发生执行器故障时，由(2)得出的系统可以描述为：

对系统引入静态输出反馈控制器uf(t)=FaKy(t)，由此构成闭环系统：

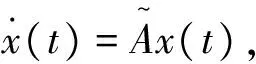
(7)

定理2对于系统(7)，如果存在标量ε>0,α>0对称正定矩阵X和矩阵K，U,V使得：

VC=CX

其中，Φ=AX+XAT+BφaiUC+(BφaiUC)T，那么有静态输出反馈控制Ki=UV-1，使得闭环系统(7)的极点落在条形区域内。

证明根据引理1可知，使闭环系统(7)的极点配置在h1和h2之间的条形区域的充分必要条件是存在对称正定矩阵X使：

(8)

其中，Π=DH(t)EX+(DH(t)EX)T。

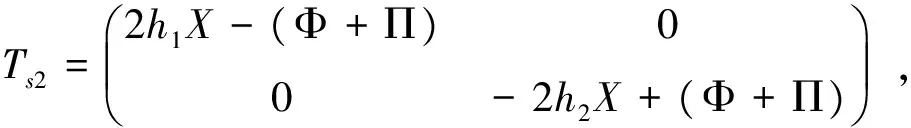
(9)

根据引理4，有：

代入(9)，有

根据Schur补引理有：

于是有:

(10)

而

代入(10)有:

根据Schur补引理整理，同时满足Ts2<0,定理得证。

3 仿真算例

第一步对于没有故障正常运行的系统，设计条形区域极点配置静态输出反馈控制器,让系统极点均落在所配置的条形区域内，即系统保持稳定；第二步考虑当系统发生执行器故障时，通过重新设计可靠控制器，使系统达到稳定。

考虑如下系统：

希望的闭环系统极点配置在h1=-3.5,h2=-0.5的条形区域内。

本文方法所设计的静态输出反馈控制器为：

此时闭环系统(6)稳定，极点均配置在所要求的条形区域内，如图1、2所示。

图1表述的是系统在无任何故障的条件下，控制器使系统保持稳定且极点均落在条形区域内。

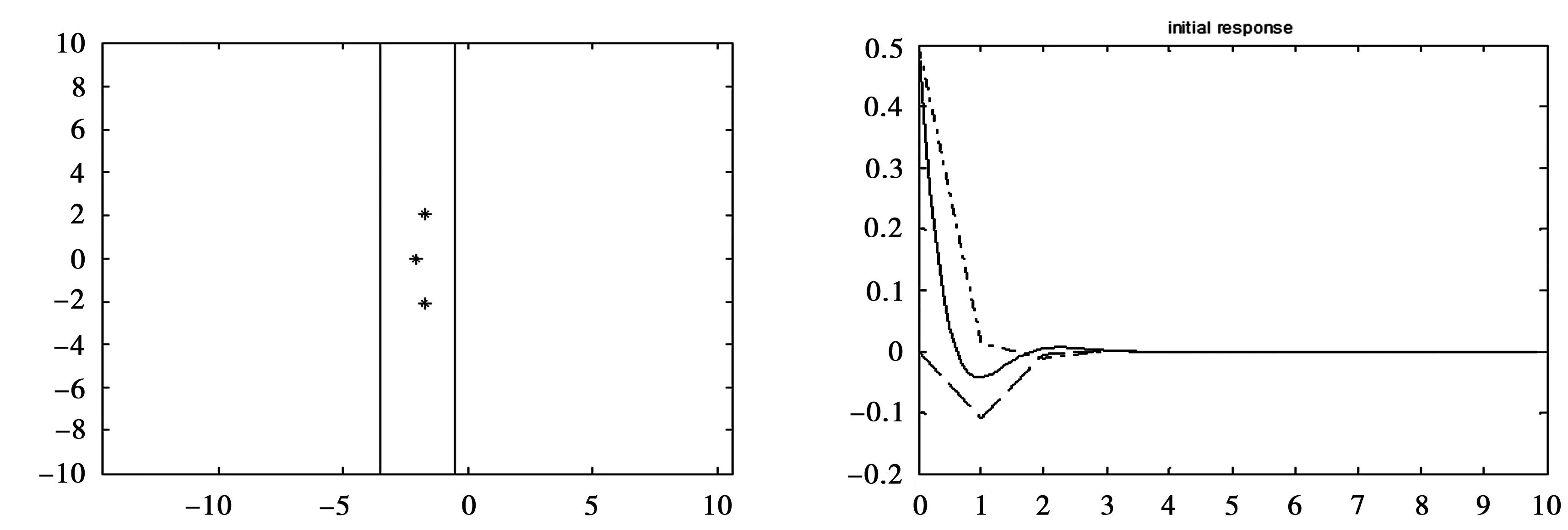
图1 系统的极点落在条形区域内(二维坐标平面) 图2 正常系统状态响应曲线

考虑执行器发生单一故障F=diag(f1,f2)，其中f1=1,0.5≤f2≤1.8，闭环系统的稳定性遭到破坏，并且系统极点未全部落在条形区域内，如图3、4所示。

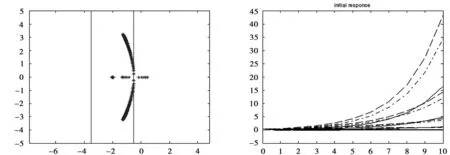
图3 当系统发生执行器故障时，极点部分跳出条形区域 图4 系统故障状态响应曲线

针对同一个故障，即F=diag(f1,f2)，其中，f1=1,0.5≤f2≤1.8，根据定理2，重新设计新的静态输出反馈控制器，即：

闭环系统渐进稳定，如图5、6所示。

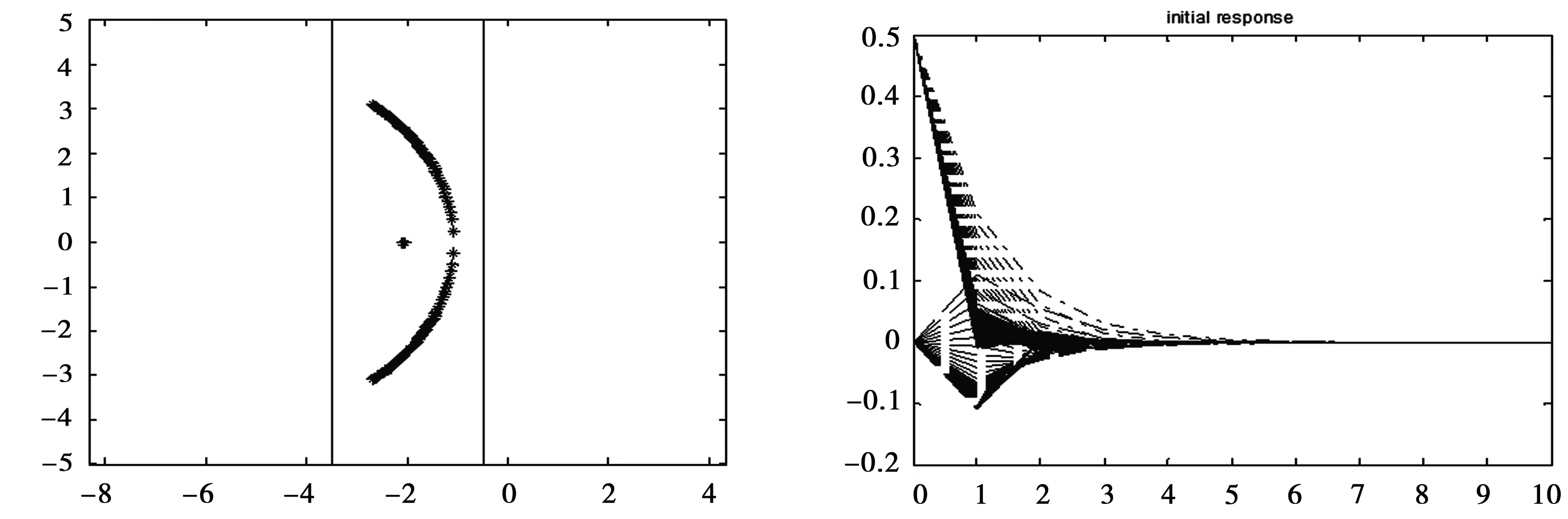
图5 系统的极点配置在条形区域内 图6 故障系统状态响应曲线

可以看到当闭环系统发生同一故障时，新设计的控制器可以使闭环系统趋向稳定，且极点均配置在所要求的区域内，由此可知可靠系统发生故障时仍能保持稳定。

4 结 论

带有不确定项的线性系统中，考虑执行器故障的情况，并进行条形区域极点配置，设计静态输出控制器。第一步在无故障的条件下，设计出使系统保持稳定的控制器；第二步，系统运行时执行器出现故障，在原控制器的调节下，无法继续保持稳定；第三步对于同一系统同一故障，经过控制器的重新设计，使其保持稳定。其中利用LMI给出了两次控制器的设计方法。最后，通过仿真确定其有效性。

[1]Furuta K , Kim S B. Pole assignment in a specified disk [J] . IEEE Transaction on Automatic Control, 1987, 32 (5): 423-427

[2]俞立,陈国定,杨马英.不确定系统的鲁棒输出反馈区域极点配置[J]. 控制理论与应用,2002(2):244-246

[3]刘满,井元伟,张嗣瀛.区域极点配置问题的研究方法[J].控制与决策,2005(3):241-245

[4]Veillette R J, Medanic J V, Perkins W R. Design of reliable control system[J].IEEE Transaction on Automatic Control,1992,37(3):770-784

[5]葛迪,姚波,王福忠. 不确定系统静态输出反馈可靠控制[J]. 计算技术与自动化,2016(1):5-8

[6]Lichao Ma, Xiuyun Meng, Zaozhen Liu, et al. Multi-objective and reliable control for trajectory-tracking of rendezvous via parameter-dependent Lyapunov functions[J].Acta Astronatica,2012,81(1):122-136

[7]王福忠,姚波,张庆灵.基于LMI双故障动态输出反馈完整性控制[J].控制理论与应用,2006,23(6):976-980

[8]葛迪,姚波. 时滞不确定系统静态输出反馈可靠控制[J]. 平顶山学院学报,2016(2):1-4

[9]谷劲柏. 一类非光滑不确定系统若干控制问题研究[D].大连:大连海事大学研究生院,2015:6-127

[10]滕青芳,范多旺.不确定系统的鲁棒状态反馈区域极点配置[J].计算技术与自动化,2006,25(1):8-10

[11]Boukas E K. Static output feedback control for stochastic hybrid systems: LMI approach[J].Automatica,2006,42(1):183-188

[12]Franke, Matthias. Eigenvalue assignment by static output feedback-on a new solvability condition and the computation of low gain feedback matrices[J].International Journal of Control,2014,87(1):64-75

[13]I R Petersen. A stabilization algorithm for a class of uncertain linear Systems[J].Syst Contr let,1987(8):351-357

(责任编辑：汪材印)

TP13

：A

：1673-2006(2017)07-0100-06

10.3969/j.issn.1673-2006.2017.07.026

2017-04-18

房志铭(1992-),辽宁葫芦岛人，在读硕士研究生，研究方向：可靠控制。