基于TOPSIS法的城市自然灾害社会脆弱性评价—以江西省为例

郭 成

安徽理工大学经济与管理学院，淮南,232001

基于TOPSIS法的城市自然灾害社会脆弱性评价—以江西省为例

郭 成

安徽理工大学经济与管理学院，淮南,232001

研究社会脆弱性旨在提升城市灾前准备和风险管理能力。基于2014年数据，在人口规模、经济条件、社会环境和建筑设施四个方面选了28个评价指标，利用SPSS软件皮尔逊相关分析筛选出19个指标作为最终的评价指标。运用TOPSIS方法建模、变异系数法赋予每个最终指标相应的权重，经过计算得到了江西省11个地级市自然灾害社会脆弱性的贴近度大小，依据贴近度将其划分为四个等级：自然灾害社会脆弱性最高的是南昌市和鹰潭市，较高的是吉安市、新余市、景德镇市和抚州市，较低的是萍乡市、九江市和上饶市，最低的是宜春市和赣州市。

自然灾害；社会脆弱性； 江西省； TOPSIS方法； 变异系数法

1 相关研究与问题提出

社会脆弱性是识别敏感人群不太可能应对自然灾害并且从中恢复的、在空间和时间上变化的复杂的、动态的社会特征[1]。Flanagan提出社会脆弱性是影响社会适应力的经济和人口因素[2]。由于经济和社会的发展状况不同，国外比中国更早地接触到了社会脆弱性，而且不同学者基于不同的角度得到了相应的研究成果。Cutter从人口规模、发展模式、经济条件、建筑环境四个方面评估了美国从1960-2008年县级区域的社会脆弱性分布变化[1]。Schmidtlein以县级市为基本单位得到了美国社会脆弱性的地理分布格局[3]。Kesavan基于一些灾害频发的区域，分析了影响社会脆弱性的主要因素，并且使用相应的方法为其改善[4]。

随着我国综合国力日益提升，国家开始重视公共安全管理，社会脆弱性逐渐成为国内学者研究的热点，各研究者根据自身研究的方向得出了一些成果。葛怡等基于中国洪涝灾害频发的实际情况，以长沙市为例，评估了水灾社会脆弱性，为今后国家防灾减灾和风险管理提供参考依据[5-6]。游温娇等从微观、宏观两方面选取社会脆弱性评价指标，从不同层面分析社会脆弱性的影响因子[7-8]。王莺等评估了中国南方干旱脆弱性，得到了地理等级区划图[9]。李畅等对湖北荆州市水灾社会脆弱性进行了时间序列和空间分布分析[10-11]。贺山峰等运用专家调查法和层次分析法评估了河南省17个地级市的社会脆弱性[12]。徐选华等用改进的突变级数法评估了四川省自然灾害社会脆弱性，并提出相应的灾前准备应对措施[13]。薛晨浩等评估了宁夏生态移民社区，得出了南高北低的地理分布态势以及影响自然灾害社会脆弱性的评价指标因子[14]。本文基于国内外学者的研究基础，以江西省11个地级市为研究对象，构建自然灾害社会脆弱性评价体系，运用TOPSIS方法计算各个评价对象的贴近度，用贴近度的大小来反映自然灾害社会脆弱性的强弱，研究结果可以为江西省应急管理人员进行区域灾前准备和风险管理提供科学依据。

2 研究区概况

江西省简称赣，总面积为16.69万km2，下辖11个地级市，省会为南昌市，属于华东地区。2014年年末，GDP为15 754.03亿元，常驻人口为4 542.2万人。江西省的地形以丘陵和山地为主，气候属中亚热带温暖湿润季风气候，全年降水量较大，且降水时间和区域分布不均，因此江西省的洪涝灾害很严重；加上江西省产业发展不均衡以及城镇化迅速推进，导致大量人口涌入城市，使该省自然灾害的社会脆弱性大大增加。

3 数据来源与研究方法

3.1 数据来源

本文数据来自2015年《江西省统计年鉴》《江西省2015年人口普查资料》和江西省11个地级市2015年统计年鉴，鉴于统计年鉴中数据非常丰富，本文从中筛选影响自然灾害社会脆弱性的各项指标原始数据。

3.2 研究方法

本文采用TOPSIS法。

3.2.1 原始数据矩阵的构建

根据对评价地区的分析，确定评价指标，则可以构成原始数据矩阵：

(1)

式中,m表示评价对象,n表示评价指标。

3.2.2 原始数据的标准化

由于各评价指标的属性和单位不统一，所以需要作规范化处理。

属性为正的评价指标，采用如下方法进行规范：

(2)

式中，i=1,2,3,…,n；j=1,2,3,…,m。

属性为负的评价指标，采用如下方法进行规范：

(3)

式中，i=1,2,3,…,n；j=1,2,3,…,m。

经过公式(2)和(3)规范化处理后得到矩阵:

(4)

3.2.3 各层次指标权重的确立

为了使评价结果客观可信，加上原始数据已作规范化处理，用变异系数法来赋权，得到的指标权重为Wi(i=1,2,3,…,n)，计算步骤如下：

(1)分别求出各个指标的平均值和标准差。

(5)

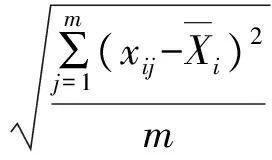
(6)

式中,i=1,2,3,…,n。

(2)计算各指标对应的变异系数。

(7)

式中,i=1,2,3,…,n。

(3)计算各评价指标的权重。

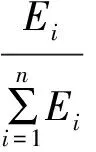
(8)

式中,i=1,2,3,…,n。

3.2.4 构成加权规范化矩阵

Zij=rijWi

(9)

式中,i=1,2,3,…,n，j=1,2,3,…,m；Wi是第i个评价指标的权重。

3.2.5 确定最优解和最劣解向量

由公式(9)得到矩阵Z，这样就可以确定各评价指标的最优解和最劣解。

(10)

(11)

3.2.6 计算各待评地区到最优解和最劣解的欧式距离

对于第i个评价对象到最优解、最劣解的欧式距离分别用下式计算：

(12)

(13)

式中,i=1,2,3,…,m。

3.2.7 计算评价区域内各评价对象的贴近度

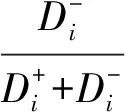
(14)

评价区域内评价对象的社会脆弱性的高低对应贴近度的大小，贴近度越大,表明该评价对象的社会脆弱性越高;贴近度越小,表明该评价对象的社会脆弱性越低。

4 方法运用与计算

4.1 评价指标的确定

由于挑选的各评价指标的属性和单位不统一(表1)，需要对指标进行规范化处理,然后根据皮尔逊相关分析筛选相关性较强的评价指标。筛选时要遵循以下原则：(1)在α=0.05时，被删指标与其他较多指标的相关性系数的绝对值在0.5以上；(2)相对同层其他指标，它的影响相对要小[15]。

经过分析与比较，可以确定筛选的指标有B12、B14、B15、B21、B31、B51、B52、C31、C32共9个指标；筛选后的评价指标个数变为19个，如表2。

表1 自然灾害社会脆弱性初始评价指标

注：“+”表示指标值越大，社会脆弱性越高；“-”表示指标值越大,社会脆弱性越低。

表2 江西省自然灾害社会脆弱性最终评价指标

注：“+”表示指标值越大，社会脆弱性越高；“-”表示指标值越大,社会脆弱性越低。

4.2 计算结果

将筛选后的评价指标构成矩阵：

(15)

式中，m=1,2,3,…,11；n=1,2,3,…,19。

对初始评价指标进行规范化处理后组成矩阵R，经过筛选得到最终矩阵A，根据公式(5)～(9)计算出各指标相应的权重，然后重组加权规范化矩阵Z。根据公式(10)和(11)得到指标最优解和最劣解的解向量：最优解Z+={0.001、0.001、0.142、0.071、0.074、0.078、0.010、0.064、0.081 、0.067、0.028、0.014、0.033、0.045、0.027、0.119、0.105、0.027、0.014}，最劣解Z-={zi/zi=0,i=1,2,3,…,19}。根据公式(12)和(13)计算研究地区到最优解和最劣解的欧式距离，并根据公式(14)计算各个研究地区的贴近度(表3)。

表3 江西省11个地级市贴近度大小排序

根据贴近度大小(表3)，将11个研究对象分为四大类，即高社会脆弱性(0.5～0.6)、较高社会脆弱性(0.4～0.5)、较低社会脆弱性(0.3～0.4)、低社会脆弱性(0.2～0.3)。自然灾害社会脆弱性最高的区域是南昌市，Ci值为0.583，最低的区域是赣州市，Ci是0.234。

5 讨论与结论

5.1 讨 论

社会脆弱性受当时经济基础、教育情况、医疗保障、基础设施等因素的影响，而且在评估时不同评价指标对其产生的影响会截然相反，这加大了社会脆弱性评估的难度。然而，TOPSIS方法恰好有效地解决了这个难题，它可以将不同向的评价指标转化为同向的评价指标，然后选择恰当的方法赋予各个指标权重，最后根据贴近度的大小进行排序。

由表3可知，江西省各地区之间的自然灾害社会脆弱性有很大的差别，最低的是赣州市，最高的是南昌市。从社会脆弱性角度分析，尽管南昌市的卫生医疗条件显著高于赣州市，但是南昌市在人口、经济、教育、基础设施等条件明显弱于赣州市，所以南昌市位居第一。在人口条件方面，南昌市的家庭户密度为189.1户/km2,而赣州市远远低于这个数值，仅为55.9户/km2；在经济条件方面，赣州市的财政收入为53.6亿元，而南昌市仅为47.3亿元，同时南昌市的人均固定资产投资为6.5万元，而赣州市只有1.8万元；在教育方面，南昌市万人学校数不及赣州市；在基础设施方面，南昌市建设用地面积占城市总面积的28%，赣州市仅为5%，而且赣州市的城市绿地覆盖率达到了42.08%，南昌市只有39.93%。综合以上有关人口、经济、教育和基础设施因素，南昌市的自然灾害社会脆弱性高于赣州市，而且高于江西省其他地级市。

5.2 结 论

研究社会脆弱性对于提升城市灾前准备和风险管理能力具有重要作用[16]。利用TOPSIS方法对江西省11个地级市的自然灾害社会脆弱性进行了评价，得出自然灾害社会脆弱性最高的是南昌市和鹰潭市，较高的是吉安市、新余市、景德镇市和抚州市，较低的是萍乡市、九江市和上饶市，最低的是宜春市和赣州市。

[1]Susan L Cutter,Christina Finch.Temporal and spatial changes in social vulnerability to natural hazards[J].Proceedings of the National Academy of Sciences of the United States of America,2008,105(7):2301-2306

[2]Barry E Flanagan,Edward W Gregory,Elaine J Hallisey,etal.A Social Vulnerability Index forDisasterManagement[J].Journal of Homeland Security and EmergencyManagement,2011,8(1):1-22

[3]Schmidtlein Mathew C,Deutsch Roland C,Piegorsch Walter W,et al. A sensitivity analysis of the social vulnerability index[J].Risk Analysis,2008,28(4):1099-1114

[4]Kesavan P C,Swaminathan M S. Managing extreme natural disasters in coastal areas[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,2006,10(5):2191-2216

[5]葛怡,史培军,刘婧,等.中国水灾社会脆弱性评估方法的改进与应用：以长沙地区为例[J].自然灾害学报,2005,14(6):54-58

[6]葛怡,刘婧,史培军.家户水灾社会脆弱性的评估方法研究：以长沙地区为例[J].自然灾害学报,2006,15(6):33-37

[7]游温娇,张永领.洪灾社会脆弱性指标体系研究[J].灾害学，2013，28(3)：215-220

[8]张永领,游温娇.基于TOPSIS的城市自然灾害社会脆弱性评价研究：以上海市为例[J].灾害学,2014,29(1):109-114

[9]王莺,王静,姚玉璧,等.基于主成分分析的中国南方干旱脆弱性评价[J].生态环境学报,2014, 23(12):1897-1904

[10]李畅,冯滔,石倩,等．洪灾社会脆弱性熵权法评价及其时间序列分析：以2001-2012年荆州市为例[J]．灾害学，2015，30(3):110-117

[11]冯滔,李畅,黄建武,等.荆州市洪灾社会脆弱性评价及其空间分异研究[J].长江科学院院报,2015,32(9):52-57

[12]贺山峰,杜丽萍,高秀华.河南省县域单元自然灾害社会脆弱性评价[J].水土保持研究，2105，22(6):293-297

[13]徐选华,张威威．基于改进突变级数法的地震灾害社会脆弱性风险评价研究：基于四川地震灾害案例[J].灾害学,2016,31(3):125-132

[14]薛晨浩,邓慧丽,苗红,等.TOPSIS 视角下西北生态移民社区自然灾害社会脆弱性评价：以宁夏为例[J].开发研究,2016(2):90-94

[15]黄润龙,管于华.数据统计分析：SPSS原理及应用[M].北京：高等教育出版社,2010:129-133

[16]Ivan Frigerio,StefaniaVentura,DanieleStrigaro,et al.A GIS-based approach to identify thespatial variability of social vulnerability to seismic hazard in Italy[J].Applied Geography,2016,6(14):13-21

(责任编辑：周博)

X43

：A

：1673-2006(2017)07-0034-04

10.3969/j.issn.1673-2006.2017.07.009

2017-05-10

郭成(1993-)，江西樟树人，在读硕士研究生，研究方向：灾害与应急管理。