基于线性反馈滑模法实现分数阶多涡卷混沌系统同步

祁 平，于海东，刘 爽，岳丽娟

(东北师范大学物理学院，吉林 长春130024)

基于线性反馈滑模法实现分数阶多涡卷混沌系统同步

祁 平，于海东，刘 爽，岳丽娟

(东北师范大学物理学院，吉林 长春130024)

将整数阶多涡卷混沌系统推广到分数阶多涡卷混沌系统.利用线性反馈控制理论和滑模控制理论，设计了线性反馈滑模控制器，在仅加一项控制器的条件下不但使该分数阶多涡卷混沌系统达到了同步且缩短了达到同步的时间.数值仿真结果表明了该方法的有效性.

分数阶多涡卷混沌系统；线性反馈法；线性反馈滑模法；混沌同步

在非线性系统中产生各种不同类型的多涡卷混沌吸引子是近年来物理学和信息科学界所研究的热点之一.1991年，Suykens等[1]首次提出了多涡卷蔡氏混沌吸引子的概念，之后人们对多涡卷混沌吸引子的产生进行了一些研究；王发强等[2]通过构造分段线性函数在四维系统中产生横向偶数个多涡卷；陈仕必等[3]用多项式和阶跃函数构造出网格多涡卷；谌龙等[4]提出一种基于平移变换的多涡卷混沌系统的构造方法.现有的文献中大多数都是整数阶多涡卷混沌系统的构造方法.而整数阶微分是分数阶微分的特例，整数阶混沌系统是对实际混沌系统的理想化处理.利用分数阶微分算子能够更准确地描述实际系统的动力学特性，由于分数阶混沌系统具有更复杂的动力学行为，所以将其用于通信保密具有更高的安全性.人们提出了很多分数阶混沌系统的同步方法，如驱动-响应同步法[5]、自适应同步法[6]、主动控制同步法[7]、线性反馈同步法[8]、滑模控制法[9]等.潘光等[10]提出了一种分数阶混沌系统同步的自适应滑模控制器的设计方法；孙宁等[11]提出使用新的分数阶滑模面的主动控制法，实现了分数阶超混沌Chen系统的投影同步.但目前文献中对分数阶多涡卷混沌系统同步研究较少.

本文在蔡氏系统的基础上进行改进，产生多涡卷混沌吸引子，从而有规律地提高了系统的复杂性，并将整数阶多涡卷混沌系统推广为分数阶多涡卷混沌系统，通过线性反馈法对该分数阶多涡卷混沌系统同步进行了研究，但同步效果不是十分理想且同步时间较长.因此，提出了线性反馈滑模法，在仅加一项控制器的条件下，对该分数阶多涡卷混沌系统进行了同步研究.结果表明，线性反馈滑模法极大地缩短了同步时间.

1 分数阶多涡卷混沌系统

在Chua系统的基础上，通过增加非线性项构造单方向多涡卷混沌系统，其无量纲状态方程为

(1)

其中α=15.2，β=18.9，ε=0.7为系统参数，即非线性函数为

(2)

图1 非线性函数f(x1)图像

当λ=1，k=1，n=2时，非线性函数f(x1)的图像如图1所示.该非线性函数由斜率为∞的键波所隔开的6个分段线性函数组成，相应的线性函数区即为涡卷区，在该非线性函数的作用下可产生由键波运动所联系的六涡卷运动.经分析可知，当λ，k值一定时，改变参数n的数值即可产生2n+2个涡卷吸引子.

当λ=1，k=1，n=2和n=3时仿真结果如图2所示.

将整数阶多涡卷混沌系统推广到分数阶多涡卷混沌系统，分数阶多涡卷混沌系统的方程为：

其中f(x1)为非线性函数，即

(4)

其中α，β，ε，λ，k为系统参数，其取值与整数阶系统中参数取值相同.选取系统的阶次q1=q2=q3=0.98，取不同的n值可以得到2n+2个多涡卷混沌吸引子.

(a)n=2六涡卷混沌吸引子

(b)n=3八涡卷混沌吸引子

当n=2时分数阶六涡卷混沌吸引子和当n=3时分数阶八涡卷混沌吸引子如图3所示.

(a)n=2六涡卷混沌吸引子

(b)n=3八涡卷混沌吸引子

由数值仿真结果可见，分数阶混沌系统可得到多涡卷混沌吸引子，拓宽了其在通信保密中的应用.

2 线性反馈法实现分数阶多涡卷混沌系统同步

系统(3)为驱动系统，响应系统为：

其中u为控制器，通过选择合适的控制器u可使初值不同的响应系统与驱动系统达到同步.

误差为

ei=yi-xi.

(6)

则误差系统为：

(7)

设控制器为

u=-ke1.

(8)

证明构造Lyapunov函数为：

(9)

(10)

根据混沌系统的有界性

(11)

其中

(12)

当k>0时，则Q为正定的，响应系统与驱动系统达到同步.

选取驱动系统的初值为(x1(0)，x2(0)，x3(0))=(0.9，0.1，0.1)，响应系统的初值为(y1(0)，y2(0)，y3(0))=(0.8，0.5，0.6)，系统阶数为q1=q2=q3=0.98，k=50，同步结果如图4所示.

(a)e1随时间t变化图像

(b)e2随时间t变化图像

(c)e3随时间t变化图像

数值仿真结果表明，线性反馈法实现了分数阶多涡卷混沌系统同步，但同步效果不是十分理想，较长时间之后才可使驱动系统与响应系统达到同步.

3 线性反馈滑模法实现分数阶多涡卷混沌系统同步

线性反馈滑模控制器为

u=u1+u2.

(13)

其中u1为线性反馈控制器，u2为滑模控制器.线性反馈控制器为

u1=-ke1=-k(y1-x1).

(14)

选取分数阶滑模面为

s(e)=CDα-1e(t).

(15)

则

(16)

设滑模控制律为

(17)

其中p，r为增益，且p>0，r>0，sgn(s)为符号函数，即

(18)

u2=-C-1(psgn(s)+rs)+α(εf(y1)-εf(x1))-αe2.

(19)

线性反馈滑模控制器为

u=u1+u2=-ke1-C-1(psgn(s)+rs)+α(εf(y1)-εf(x1))-αe2.

(20)

证明考虑如下的Lyapunov函数为

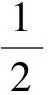
(21)

则

(22)

当pmin>0，rmin>0时，系统的轨迹在控制律作用下达到滑模面，此时误差系统为：

(23)

构造Lyapunov函数为：

(24)

(25)

其中

(26)

当k>0时，则Q为正定的，响应系统与驱动系统达到同步，根据混沌的有界性，在线性反馈滑模控制器的作用下驱动系统与响应系统可以达到同步.

选取驱动系统的初值为(x1(0)，x2(0)，x3(0))=(0.9，0.1，0.1)，响应系统的初值为(y1(0)，y2(0)，y3(0))=(0.8，0.5，0.6)，且k=50，p=0.2，r=26，数值仿真结果如图5所示.

(a)e1随时间t变化图像

(b)e2随时间t变化图像

(c)e3随时间t变化图像

线性反馈滑模法较好地实现了分数阶多涡卷混沌系统同步，线性反馈滑模法与线性反馈法对比可知，在仅加一项控制器的条件下线性反馈滑模法缩短了2个系统的同步时间.

4 结论

本文在Chua氏系统的基础上构造出整数阶多涡卷混沌系统，并将其转变为分数阶多涡卷混沌系统，基于线性反馈法和滑模变结构理论，根据Lyapunov稳定性理论和滑模可达条件设计了一个线性反馈滑模控制器，在仅加一项控制器的条件下，实现了分数阶多涡卷混沌系统的同步.数值仿真结果表明，线性反馈滑模法比线性反馈法的控制效果好，实现同步时间短，控制器相对简单，易于实现，应用前景广阔.

[1] SUYKENS J，VANDEWALLE A K. Quasilinear system and design ofn-double control (n=1,2,3,4，…)[J].Circuits Devices & Systems Iee Proceedings G，1991,138(5):595-603.

[2] 王发强，刘崇新，逯俊杰.四维系统中多涡卷混沌吸引子的仿真研究[J].物理学报，2003，52：25-33.

[3] 陈仕必，曾以成，徐茂林.用多项式和阶跃函数构造网格多涡卷混沌吸引子及其电路实现[J].物理学报，2011，60(2)：3071-3077.

[4] 湛龙，彭海军，王德石.一类多涡卷混沌系统构造方法研究[J].物理学报，2008，57：3337-3341.

[5] 周平，赵鹏. 混沌系统的驱动-响应同步[J].重庆大学学报，2002,15(12):77-79.

[6] SINHA S C ， HENRICHS J T ，RAVINDRA B. A general approach in the design of active controllers for nonlinearsystems exhibiting chaos[J] International Journal of Bifurcation and Chaos,2000，10 (1)：165-178.

[7] 王兴元,朱全龙,张晓鹏.基于三种方法的新Lü混沌系统的同步[J]. 物理学报，2011,60(10):100510-1-9.

[8] PYRAGAS K. Continuous control of chaos by self-controlling feedback [J].Physics Letters A,1992,170(6):421-428.

[9] 曹鹤飞，张若洵. 基于滑模控制的分数阶混沌系统的自适应同步[J].物理学报，2011,60(5):050510-1-5

[10] 潘光，魏静.一种分数阶混沌系统同步的自适应滑模控制器设计[J].物理学报，2015,64(4):040505-1-6.

[11] 孙宁，张化光，王智良. 基于分数阶滑模面控制的分数阶超混沌系统的投影同步[J].物理学报，2011,60(5):050511-1-7.

(责任编辑：石绍庆)

Linearfeedbackslidingmodecontrollerforsynchronizationoffractionalmulti-scrollchaoticsystem

QI Ping，YU Hai Dong，LIU Shuang，YUE Li Juan

(School of Physics，Northeast Normal University，Changchun 130024，China)

In this paper，the fractional chaotic system is extended from integer order chaotic system.We design a linear feedback sliding mode controller based on the theory of learning feedback control and the theory of sliding mode control.The synchronization of the fractional multi-scroll chaotic systems is achieved.The synchronization time of the fractional multi-scroll chaotic systems is shortened by linear feedback sliding mode control law.The result of numerical simulation shows the effectiveness of the proposed controller law.

fractional multi-scroll chaotic system；linear feedback；linear feedback synovial；chaos synchronization

1000-1832(2017)03-0083-05

10.16163/j.cnki.22-1123/n.2017.03.018

2016-09-02

国家自然科学基金资助项目(10847110),吉林省自然科学基金资助项目(201115008).

祁平(1986—)，女，硕士研究生；通信作者：岳丽娟(1963—)，女，博士，教授，主要从事非线性混沌控制与同步研究.

TP 271 [学科代码] 120·20

A