一类病毒反应系统的亚纯可积性

杨双羚，周 冉

(1.东北师范大学数学与统计学院，吉林 长春 130024； 2.吉林大学数学学院，吉林 长春 130012)

一类病毒反应系统的亚纯可积性

杨双羚1，周 冉2

(1.东北师范大学数学与统计学院，吉林 长春 130024； 2.吉林大学数学学院，吉林 长春 130012)

基于微分Galois理论以及动力系统可积性理论，采用理论分析方式，在已有文献研究基础上，讨论了一类病毒反应系统的亚纯可积性，证明了该系统不存在两个函数独立的亚纯首次积分，并给出了亚纯不可积性的充分条件.

微分Galois理论；Kovacic算法；首次积分；可积性

考虑病毒反应模型[1]

(1)

其中：x，y，z分别表示健康细胞浓度、感染细胞浓度以及病毒浓度；λ，β，a，k，u是具有生物学意义的正参数.该模型由Nowak提出，作为刻画病毒动力系统相互作用的重要模型而被广泛研究.[2-4]到目前为止，关于该模型可积性的研究很少，文献[5]利用拟齐次多项式理论研究了该模型的多项式首次积分.

本文主要考虑系统(1)亚纯首次积分的存在性与唯一性.

1 预备知识

下面主要介绍微分Galois理论[6]的相关定义与结论.考虑复全纯向量场

(2)

其中t∈C是复时间，M是n维解析流形.如果非常值函数Φ(x)：U→C沿着系统的任意解都是常数，则称函数Φ(x)是系统(2)的首次积分，其中U是M中的开集.如果向量场(1)有两个(一个或者没有)线性无关的首次积分，则相应称向量场(1)完全可积(部分可积或者不可积).假设系统(1)有非平凡解φ(t)，记Γ={φ(t)}是对应的相曲线，则系统(1)沿Γ的变分方程是

(3)

其中TΓM是TM限制在Γ上的向量丛.

记法丛F=TΓM/TM，相应的自然投影π：M→F，则变分方程(1)可以降低维数，约化成法向变分方程

(4)

注意到方程(3)是线性微分方程，因此考虑相应的微分Galois群G以及单位联通分支G0.[6]

下面结果解释了系统(3)亚纯首次积分的存在性与单位联通分支G0之间的关系.

引理1[7]假设系统(3)在Γ某邻域上有m个函数独立的亚纯首次积分，则：

(1) 如果m=n-1，那么G0={1}；

(2) 如果m=n-2，那么G0是交换群；

(3) 如果m=n-3，那么G0是可解群.

一般地，计算给定线性微分方程组的微分Galois群G以及单位联通分支G0是十分困难的，但对于二阶线性微分方程，文献[7]给出了完整的算法.考虑二阶微分方程

ξ″=rξ，r∈C(x).

(5)

引理2[8]方程(5)的微分Galois群G必为如下四种情形之一：

(Ⅰ)G可约，即共轭于某个上三角矩阵群；

(Ⅱ)G共轭于代数群的某个子群

且情形(1)不成立；

(Ⅲ)G是有限群，且情形(1)和情形(2)不成立；

(Ⅳ)G=SL(C，2).

引理3[8]引理2前三种情形成立的必要条件分别是：

(1)r(x)的每个极点要么阶数是偶数，要么阶数是1；r(x)在无穷远点∞的阶数要么是偶数，要么大于2.

(2)r(x)至少有一个极点的阶数是2或者大于2的奇数.

(3)r(x)的每个极点阶数不超过2，r(x)在无穷远点∞的阶数至少为2；如果r(x)可分式展开为

则

下面介绍如何用Kovacic算法判定引理2中情形(Ⅱ)是否发生.完整的算法可以参见文献[9]附录部分.情形(Ⅱ)的Kovacic算法如下：

步骤3 对于步骤二中成立的情形，寻找一个次数为d的首一多项式P满足

P‴+3θP″+(3θ2+3θ′-4r)P′+(θ2+3θθ′+θ3-4rθ-2r′)P=0.

如果存在满足上述条件的多项式，则情形(Ⅱ)成立.如果对步骤二成立的每种情形，都不存在这样的多项式，则情形(Ⅱ)不成立.

2 主要结论

相应的法向变分方程组(NVE)为

易知上述方程组等价于二阶方程

(6)

(7)

由亚纯联络[8]，方程(7)的微分Galois群同构于方程(6)的微分Galois群，故只需研究方程(7)的微分Galois群.注意到方程(8)的奇点是0和∞，即ρ={0，∞}，其中0的阶数是2，∞的阶数是1.由引理3，只有情形(Ⅱ)或情形(Ⅳ)可能成立，情形(Ⅲ)不成立.又因为二阶有限Galois群的单位连通分支G0={1}，故系统(7)不是完全可积的，即不存在两个线性无关的亚纯首次积分，进而考虑系统(7)亚纯首次积分的存在性.若系统存在一个首次积分，则情形(Ⅱ)成立.下面利用k-算法：

步骤2 容易知道

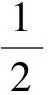
步骤3 经简单计算，有

设多项式P(τ)=b0+b1z+…+baτa，代入得

对比同次幂系数，易知满足上述条件的多项式总是存在.

综上可得：

[1] MAY R M，NOWAK M A.Virus dynamics：mathematical principles of immunology and virology[M].New York：Oxford University Press，2000：63-117.

[2] SMITH H L，DE LEENHEER P.Virus dynamics：a global analysis[J].SIAM J Appl Math，2003，63(4)：1313-1327.

[3] PERELSON A S，NELSON P W.Mathematical analysis of HIV-1 dynamics in vivo[J].SIAM Review，1999，41(1)：3-44.

[4] MIN L，SU Y，KUANG Y.Mathematical analysis of a basic virus infection model with application to HBV infection[J].Journal of Mathematics，2008，38(5)：268-288

[5] VALLS C.Invariant algebraic surfaces for a virus dynamics[J].Z Angew Math Phys，2015，66(4)：1315-1328.

[6] KATZ N M.On the calculation of some differential Galois groups[J].Inventiones Mathematicae，1987，87(1)：13-61.

[7] LI W，SHI S.Galoisian obstruction to the integrability of general dynamical systems[J].J Differential Equations，2012，252(10)：5518-5534.

[8] MORALES-RUIZ J J.Differential Galois theory and non-integrability of Hamiltonian systems[M].Boston：Birkhauser，1999：11-26.

[9] SHI S，LI W.Non-integrability of generalized Yang-Mills Hamiltonian system[J].Discrete Contin Dyn Systems A，2013，33(4)：1645-1655.

(责任编辑：李亚军)

Onmeromorphicintegrabilityofavirusdynamics

YANG Shuang-ling1，ZHOU Ran2

(1.School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China； 2.College of Mathematics，Jilin University，Changchun 130012，China)

Based on the differential Galois theory，the meromorphic integrability of a virus dynamics is proved by using the so-called Picard-Vessiot theory and Kovacic’s algorithm.A sufficient condition for the non-existence of meromorphic first integrals of this system is presented.

differential Galois theory；Kovacic’s algorithm；first integral；integrability

1000-1832(2017)03-0018-04

10.16163/j.cnki.22-1123/n.2017.03.005

2016-03-09

国家自然科学基金青年科学基金资助项目(11501242).

杨双羚(1991—)，女，硕士，主要从事概率统计与随机分析研究.

O 175.8 [学科代码] 110·67

A