N=2的Loop Ramond超共型代数的导子和自同构

付佳媛，张志兰

(中国传媒大学理学院，北京100024)

N=2的Loop Ramond超共型代数的导子和自同构

付佳媛，张志兰

(中国传媒大学理学院，北京100024)

给出了N=2的Loop Ramond超共型代数RL的定义，并进一步确定了其导子代数和自同构群.

N=2的Loop Ramond超共型代数；导子；自同构群

1 预备知识

超共型代数是近些年新兴的一类李超代数.Kac等[1-2]已经给出了超共型代数的所有分类.对于N=2 的超共型代数，目前也有了一些研究结果.[2-5]文献[6]给出了N=2 Ramond超共型代数中间序列模的分类.

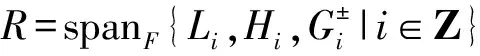
李超代数运算定义如下：

[Litk，Ljtl]=(i-j)Li+jtk+l， [Hitk，Hjtl]=0，

(1)

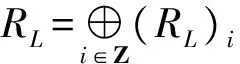
2 RL的导子代数

记RL的导子代数为DerRL，内导子代数为adRL.易知

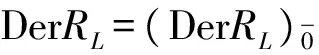
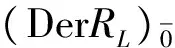
(DerRL)i={D∈DerRL|D(RL)j⊆(RL)i+j，j∈Z}.

对于Di∈(DerRL)i，称Di为i次齐次导子.不难证明下面结论：

引理2.1 对任意的D∈DerRL，则D有如下形式：

这里Di∈(DerRL)i，且对任意的x∈RL，只有有限个i∈Z使得Di(x)≠0.

引理2.2 对任意的i≠0，D∈(DerRL)i是内导子.

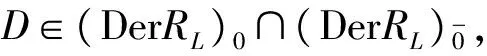
D(Litk)=Litkfi，k(t)，D(Hitk)=Hitkfi，k(t)，

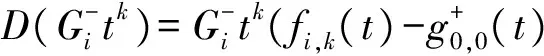
(2)

D(Xitk)=Xitkfi，k(t)，

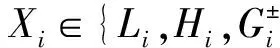
D(X0t)=0，

即f0，1(t)=0.令f1，0(t)=f(t)∈F[t，t-1]，则fi，k(t)=if(t)，因此

D(Xitk)=iXitkf(t).

显然D=-ad(L0f(t))∈adRL，从而得到下面引理.

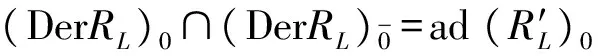
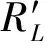
D=ad(L0f(t)+H0g(t))=Dρ，

即ρ(tk)=itk(-f(t)±g(t))，从而g(t)=0.令k=0，则-if(t)=ρ(1)=0，i∈Z，即D=0.

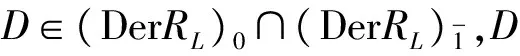
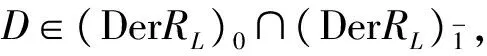
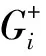
综上，有下面结论成立.

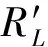
3 RL的自同构群

记RL的自同构群为AutRL，则L0，H0是RL的ad-局部有限元，从而下面结论成立.

引理3.1σ(L0)，σ(H0)∈spanF{L0，H0}，∀σ∈AutRL.

令σ(L0)=a1L0+a2H0，σ(H0)=b1L0+b2H0，则可求出a1=±1.将σ作用在[H0，Hitk]=0上可求得b1=0.故上式可改写为

σ(L0)=±L0+aH0，σ(H0)=bH0.

(3)

对于映射η：Z×Z→F[t，t-1]，记η(i，k)=ηi，k(t)∈F[t，t-1]，Finv[t，t-1]为F[t，t-1]中可逆多项式集.易知Finv[t，t-1]是一个乘法群.

引理3.2 对任意的σ∈AutRL，存在η∈Hom(Z×Z，F[t，t-1])，ε，ξ∈{±1}，a∈F，q(t)∈Finv[t，t-1]，使得：

σ(Litk)=ηi，k(t)(εLεi+aHεi)，σ(Hitk)=ξηi，k(t)Hεi，

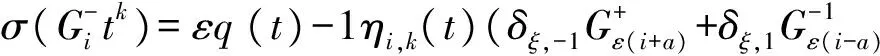
(4)

其中ηi，k(t)∈F[t，t-1]满足η0，0(t)=1，且ηi+j，k+l(t)=ηi，k(t)ηj，l(t)，∀i，j，k，l∈Z.

证明分情况证明此命题.

情形1σ(L0)=L0+aH0.

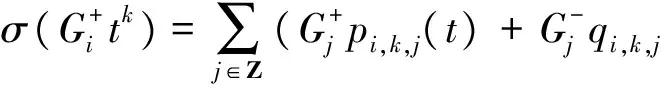
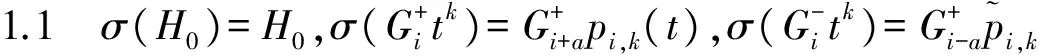
σ(Litk)=Liηi，k(t)+aHiηi，k(t)，σ(Hitk)=Hiηi，k(t)，

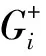
其中ηi+j，k+l(t)=ηi，k(t)ηj.l(t)，η0，0(t)=1，a∈F，p(t)∈Finv[t，t-1].

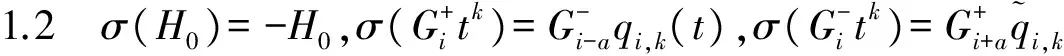
σ(Litk)=Liηi，k(t)+aHiηi，k(t)，σ(Hitk)=-Hiηi，k(t)，

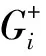
其中ηi+j，k+l(t)=ηi，k(t)ηj，l(t)，η0，0(t)=1，a∈F，q(t)∈Finv[t，t-1].

用类似方法可讨论a=-1的情况.

情形2σ(L0)=-L0+aH0.

子情形2.1

σ(Litk)=-L-iηi，k(t)+aH-iηi，k(t)，σ(Hitk)=H-iηi，k(t)，

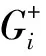
这里ηi+j，k+l(t)=ηi，k(t)ηj，l(t)，η0，0(t)=1，a∈F，p(t)∈Finv[t，t-1].

子情形2.2

σ(Litk)=-L-iηi，k(t)+aH-iηi，k(t)，σ(Hitk)=-H-iηi，k(t)，

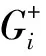
这里ηi+j，k+l(t)=ηi，k(t)ηj，l(t)，η0，0(t)=1，a∈F，q(t)∈Finv[t，t-1].

记Hom(Z×Z，F*)为加群Z×Z到乘群F*的同态，μθ为其单位元.记Hom(Z×Z，F)为Z×Z到F的加群同态，νθ为其单位元.

若ηi，k(t)∈F[t，t-1]，满足ηi+j，k+l(t)=ηi，k(t)+ηj，l(t)以及η0，0(t)=1，易知

ηi，k(t)=μ(i，k)tν(i，k)∈Finv[t，t-1]，

其中μ∈Hom(Z×Z，F*)，ν∈Hom(Z×Z，F).由引理3.2，

AutRL={σ(μ，ν，ε，ξ，a，q(t))|μ∈Hom(Z×Z，F*)，ν∈Hom(Z×Z，F)，

ε，ξ∈AutZ，a∈F，q(t)∈Finv[t，t-1]}，

AutRL的单位元是σ(μθ，νθ，1，1，0，1)，并且

其中

μ(i，k)=μ2(i，k)μ1(ε2i，ν2(i，k))，ν(i，k)=ν1(ε2i，ν2(i，k)).

(5)

易证μ∈Hom(Z×Z，F*)，ν∈Hom(Z×Z，F).

令τ=〈σ(μ，ν，1，1，a，q(t))|σ∈AutRL〉，易证τ是AutRL的自同构群，从而有如下定理：

定理3.1 (1) AutRL同构于

Hom(Z×Z，F*)×Hom(Z×Z，F)×AutZ×AutZ×F×Finv[t，t-1]；

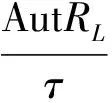
[1] KAC V G，VAN DE LEUER.On classification of superconformal Algebras[M].Singapore：World Scientific，1988：1-30.

[2] CHENG S，KAC VG.A newN=6 superconformal algebra[J].Comm Math Phys，1997，186：219-231.

[3] DORRZAPF M.Superconformal field theories and their representations [D].Cambridge：University of Cambridge，1995.

[4] DORRZAPF M.The embedding structure of unitaryN=2 minimal model [J].Nucl Phys B，1998，529：639-655.

[5] FU J Y，JIANG Q F，SU Y C.Classification of modules of intermediate series over RamondN=2 supercomformal algebras [J].J Math Phy，2007，48(4)：105-110.

[6] KIRITSIS E.Character formula and the structure of the represetations of theN=1，N=2 superconformal algebras [J].Int J Mod Phys A，1988，3：1871-1906.

(责任编辑：李亚军)

DerivationandautomorphismgroupofLoopRamondN=2superconformalalgebra

FU Jia-yuan，ZHANG Zhi-lan

(School of Science，Communication University of China，Beijing 100024，China)

The definition of the Loop RamondN=2 superconformal algebras is proposed.The derivation algebra and the automorphism group are investigated.

Loop RamondN=2 superconformal algebra；derivation；automorphism group

1000-1832(2017)03-0001-04

10.16163/j.cnki.22-1123/n.2017.03.001

2015-12-01

国家自然科学基金资助项目(11271056).

付佳媛(1978—)，女，博士，副教授，主要从事李(超)代数研究；通信作者：张志兰(1989—)，女，硕士，主要从事李(超)代数研究.

O 152.5 [学科代码] 110·21

A