基于矢量定姿原理的高精度星像片姿态计算模型

王 飞

(西安航空学院 飞行器学院，陕西 西安 710077)

基于矢量定姿原理的高精度星像片姿态计算模型

王 飞

(西安航空学院 飞行器学院，陕西 西安 710077)

在航空航天技术中，为了能够精确确定卫星的位置，卫星需要拍摄星空中的恒星，得到星像片，利用星像片上的信息来得到卫星的姿态信息，这些姿态数据在卫星定位中起到了重要的控制作用。基于矢量定姿原理和摄影测量中的共线方程，文中设计了一个通过星像片来获取卫星姿态信息的计算模型。同时通过计算恒星视位置，查阅星表数据库，改善了卫星姿态计算算法的精度。经过具体实验，姿态角计算可达到≤mq，mg≤0.8和mk≤5的精度。

姿态角；星像片；摄影测量；共线方程

伴随着空间、计算、摄影、图像传输和处理等技术的发展，航天摄影测量技术得已应用。该技术属于摄影测量学科，其通常使用宇宙飞船、人造地球卫星或者航天飞机做运载工具，使用传感器技术来遥控感知地球表面[1-3]。得到这些信息之后，经过处理，最后绘制成地图。该技术尤其是应用在军事方面，可以确定目标点位，编制成动态地图。

美国在上世纪50年代便开始研究该技术的原理，60年代美国执行阿波罗计划时，星相机被设置在月球探测器上，后来美国航天飞机上的星相机组成了测量相机系统。目前，该技术向着低功耗、轻量化、高精度和高可靠性的方向发展，在国外已较为成熟，成为了空间探测器上必备姿态敏感部件[4-6]。因为我国航天技术的发展，星相机技术也被国内科研人员研究多年[7-9]，目前对该技术的研究仍处于快速发展时期，主要集中在自主导航、紫外星相机等方面[10-16]。

利用星相机拍摄图片进行姿态计算的主要原理是，双矢量定姿原理和摄影测量的共线方程。本文基于以上原理，为了能够高精度实时计算航天器的姿态信息，提出了一个高可靠性的算法。其具体流程如下：(1)经过图像处理识别出星像片中的星像点和框标点，得到这些信息后，将星像点和框标点统一到后者坐标系中；(2)查阅星表数据库，将被拍摄的恒星坐标找出，并对这些视位置进行计算；(3)按照共线方程，把对应的两个坐标做成误差方程，引入最小二乘法，从而得到姿态角；(4)用姿态角计算其他信息。

1 星相机的精度

星相机是一种安装在航天器上的精密仪器，主要功能是拍摄恒星。其在实际应用中需要了解恒星的特性，包括到地球的距离、空间速度、大小、温度和亮度等。这些具体的信息均可从数据库中查到。综合而言，星相机拍摄的恒星需要具备3个显著特点：无穷远的、微弱的、特定光谱特性。此外，星相机的精度指标主要指的是姿态测量精度。令mx,y是坐标测量精度，L衡量了星相机幅面的大小，p是未知数个数，f是焦距，n是坐标个数，mφ,ωmk是姿态角误差，则测量姿态角预期精度的估计公式为

(1)

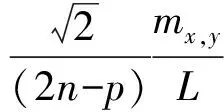
(2)

显然公式中的两个精度，f和L均有负相关的关系。为了降低姿态角误差，应该加大f和L。

2 恒星像片的判认和测量

恒星像片中有价值的信息是星相点和框标点。星相点和背景相比，两者的灰度级相差较大。所以，通过图像处理技术可轻松确定出星像点和框标点的坐标。

2.1 框标点的确定

选定一个适中的灰度门限，找到最小灰度级的象元，其所在行列的灰度值和这一灰度门限值之差是最小，则该象元便是要找的框标点。其所在的行列数就是框标点的x，y坐标。

2.2 星相点的确定

找到最小灰度级的象元，其灰度值满足下式，则该象元就是星相点，即判读出星相点。

G-M<5δ

(3)

其中，G是象元的灰度值;δ是象元灰度值和平均值之差的均方根;M是象元灰度值的平均值。令N表示图像中的行列数;g(i,j)表示象元的灰度值，则δ和M可按照下面的公式计算

(4)

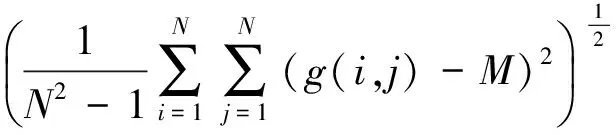
(5)

判读出星相点之后，就可以用适当的数学处理方法得到星相点的质心坐标。在本文中质心法被用来确定星相点的中心坐标，令xpi和ypi表示星相点中心坐标，N表示星相点的象元个数，f(i,j)表示星相点的象元行列值，则其计算公式如下

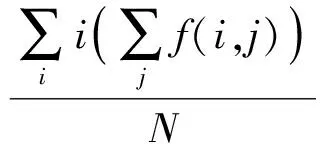
(6)

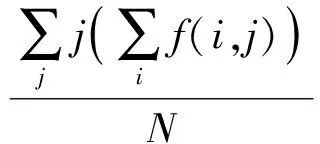
(7)

上面得到的各个点的坐标是扫描坐标系的值，为了将坐标统一到框标坐标系，需要了解框标点的测量值和鉴定值，然后列出误差方程，得到平移系数ai和旋转系数bi。令x′和y′代表修正后的框标点、星相点坐标，x和y表示测量值，其计算公式为

(8)

3 自动找星

3.1 概略星区计算

令星相机主光轴在天球坐标系中指向为(a0,δ0)，根据这一指向搜索出该星象片覆盖的恒星，做出局部星表录入数据库，其主要依据为

Δα=arccos(cos(αi-α0)×cos(δi-δ0))≤R

(9)

其中,αi和δi是恒星天球的坐标;R是星相机半视场角，单位是弧度。

3.2 选择定标星

首先以像主点为中心，选出3个服从均匀分布的定标星，这3个点组成三角形，而三角形的内角不能<15° ，星相点距离像点必须>15 mm，使用这3个坐标挑出对应的恒星。选择好定标星后，根据角距找出对应的恒星，角距的计算如下

(10)

其中，f是星相机的焦距；x、y是星相点的坐标。

3.3 自动找星

自动找星的第一步是计算底片常数，已知定标星的坐标，计算出理想坐标(ξ,η)，其计算公式如下

(11)

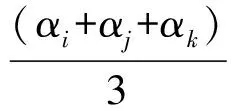
(12)

然后根据上面的计算结果(ξ,η)，计算天球坐标(a,δ)。

(13)

将(α,δ)代入，ε3=0.005，查找星表中对应的恒星

(14)

3.4 恒星视位置计算

按照定义，在某一历元中，恒星视位置指的是恒星相对于地球质心的位置。一般情况下，其需要经过各种修正才能得到，这些修正主要是自行、岁差、章动和光行差等。岁差指的是不同的历元中平赤道坐标系变化导致的不同；章动指的是同一历元中真赤道和平赤道坐标系的不同；若定向历元和观测历元不同，需要自行修正；由于视位置是基于地球质心的，具体操作需要周年光行差修正。

3.5 星像片姿态角计算

如下图所示，星象空间坐标系被由此建立。图中o是星象摄影机物镜中心;o′o是摄影机的主光轴方向;O′-XYZ是天球坐标系。图中的相片就是正片的位置，O′o轴线和天球上的赤经α0、赤纬δ0的方向相同，按照右手坐标系的规则，k是正向相片y轴和子午面之间的夹角。

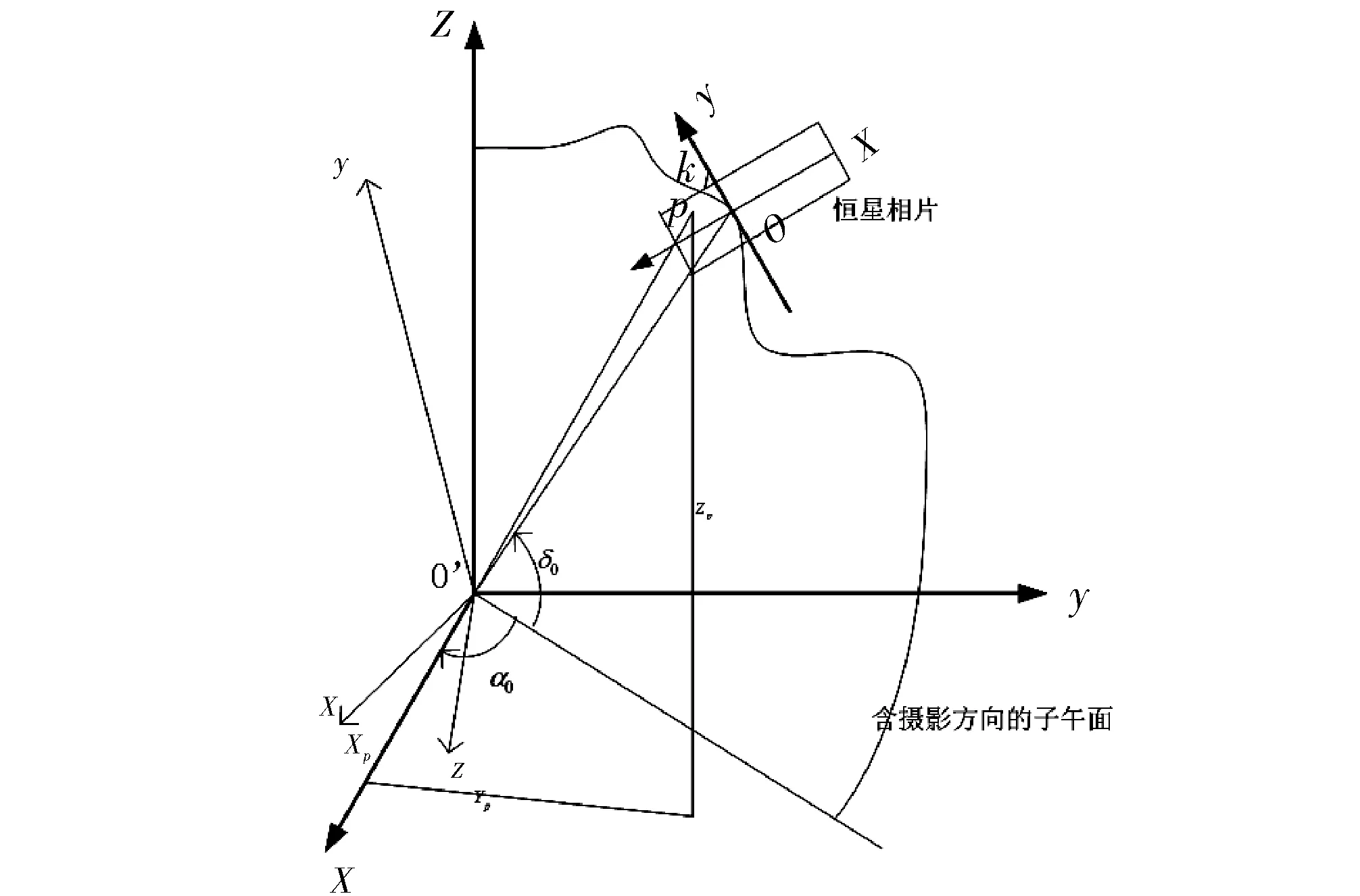
图1 星像空间坐标系在天球系中位置

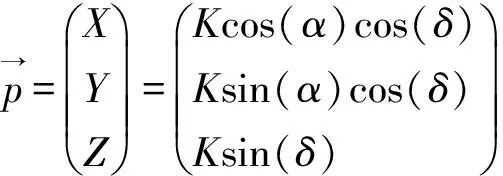
(15)

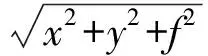
(16)

该公式可得出天球坐标和恒星影像的关系为

(17)

这里A=cos(α)cos(δ)，B=sin(α)cos(δ)，C=sin(δ)。所以，按照上式便可得到以下观测方程

(18)

其中的系数表达式为

(19)

所以按照上式可以得到观测方程式，lx和ly是常数项。相片上的每个像素均能够列出两个观测方程式，故必须有5颗恒星才能计算。实际应用中，每张相片不止这么多像素，用最小二乘法就可以计算出卫星的姿态信息。在具体的计算过程中，每次把未知数代入，计算得到新系数、常数项和法方程。循环往复，使得修正值小于规定的误差，也就是外方位角<0.5×10-7，内方位元素<0.001 mm，畸变系数<0.2×10-8。

4 结果与分析

为了验证本文算法的实用性和可靠性，63张恒星像片被实际处理，其精度统计如下表。

表1 卫星1三航段星像片精度表

表2 卫星2三航段星像片精度表

经过63张实测恒星像片数据的处理，根据以上的表格，单位权中误差m0约位于5 μ，姿态角精度为mα，mδ≤0.8，mk≤5。

5 结束语

文中基于矢量定姿原理提出了一个卫星姿态信息计算模型。通过查阅星表数据库以及计算恒星视位置，提高了卫星姿态计算算法的精度，具有一定的参考价值。

[1] 潘良,周海渊,张同双,等.一种双星敏感器联合确定船体姿态方法[J].中国惯性技术学报, 2015(3):334-338.

[2] 王顺亮.基于GNSS的高轨卫星定姿技术研究[D].南京:南京航空航天大学,2013.

[3] 陈军.基于星敏感器/陀螺的卫星姿态确定技术研究[D].长沙:国防科学技术大学,2013.

[4] 李诚良.卫星姿控系统参数辨识与递推控制方法研究[D].哈尔滨:哈尔滨工业大学,2014.

[5] 甘庆波.利用星敏感器的卫星及星座自主定轨方法研究与应用[J].天文学报,2012,53(4):355-356.

[6] 易航,徐波,高有涛.导航星座长期自主定轨半物理仿真系统研究[J].系统仿真学报,2013, 25(5):950-956.

[7] 王欣宇,范百兴,王同合,等.动态位姿激光跟踪测量定向解算精度分析[J].测绘工程,2017,26(3):56-59.

[8] 肖岩,叶东,孙兆伟.面向三轴气浮台的室内星敏感器定姿方法[J].哈尔滨工业大学学报,2016,48(10):51-56.

[9] 江丹,邓新蒲,吴京,等.几何扩展卡尔曼滤波算法在卫星姿态确定系统中的应用[J].传感器与微系统,2016,35(9):156-160.

[10] 臧强,高晶敏,杨鸿波,等.基于四频差动激光陀螺/星敏感器的卫星定姿算法[J].电光与控制,2016(3):87-91.

[11] 淡鹏,陈剑平.自旋卫星几何定姿限制条件及误差分析[J].电子科技,2016(5):62-66.

[12] 尹剑,杨萌,张琬琳,等.捷联惯导飞行器旋转矢量姿态优化仿真研究[J].计算机仿真,2016, 33(7):147-152.

[13] 刘源,谢睿达,赵琳,等.基于机器学习的大视场星敏感器畸变在轨标定技术[J].红外与激光工程,2016,45(12):275-283.

[14] 刘林,唐猛.基于模型设计方法的混合磁悬浮平台的控制设计及实现[J].工程设计学报,2012,19(6):428-433.

[15] 张超,孙延超,李传江,等.基于频域分析的挠性卫星姿态高稳定度控制[J].电机与控制学报,2016,20(12):92-100.

[16] 熊亚洲,武延鹏,程会艳.多探头星敏感器星图融合姿态确定精度[J].中国惯性技术学报,2016,24(5):612-618.

The Calculation Model of High Precision Satellite Photo Pose Vector Based on the Principle of Attitude Determination

WANG Fei

(School of Aircraft,Xi’an Institute of Aeronautics and Astronautics, Xi’an 710077, China)

In the aerospace technology, in order to achieve precise positioning of satellite attitude,we must be in the sky of stars shooting through the attitude information processing for satellite access to satellite photograph, the attitude data played an important role in satellite positioning. Vectororientation principle and collinear equation in photogrammetry based on the design of a high precision satellite photo attitude calculation model, calculation method and catalog database using the apparent positions of the stars, improves the ability of judging star is greatly improved, the photograph of the satellite attitude accuracy and reliable. After a specific experiment, the attitude angle can be calculated to be less than or equal to 0.8 and 5.

attitude angle; star photo; photogrammetry; collinear equation

2017- 03- 16

王 飞(1987-)，男，硕士，助教。研究方向：飞行器设计、航天器惯性导航。

10.16180/j.cnki.issn1007-7820.2017.09.041

TP273

A

1007-7820(2017)09-152-04