LNG独立C型液舱晃荡特性试验研究

刘 戈， 林 焰*,2， 管 官， 李 冰

( 1.大连理工大学 船舶工程学院， 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024 )

LNG独立C型液舱晃荡特性试验研究

刘 戈1， 林 焰*1,2， 管 官1， 李 冰1

( 1.大连理工大学 船舶工程学院， 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024 )

与LNG运输船不同，LNG加注船的液舱会经常处于部分装载状态，故液舱晃荡问题必须予以考虑．由于目前LNG加注船主要采用独立C型液舱，针对该种形式液舱，使用模型试验，系统研究了不同载液高度、激励频率及激励幅值影响下的晃荡情况．讨论分析了其晃荡时自由液面的波形特征，对中间液深工况下，自由液面在舱顶的影响下出现的波形进行分类．通过对晃荡荷载的统计分析，发现产生最大荷载的激励频率与理论固有频率有所偏差，且该偏差会随着液位的升高而降低．此外，在荷载空间分布方面，载液高度为0.6Di(Di为模型液舱直径)时，自由液面在封头处破碎严重，会对液舱封头上部产生较大冲击；而在0.8Di载液高度时，应充分考虑0.8fn(fn为理论固有频率)至1.2fn激励区间内的顶部冲击荷载．

晃荡；独立C型液舱；LNG加注船；试验研究

0 引 言

随着清洁能源的推广，液化天然气(liquid natural gas，简称LNG)的使用范围越来越广，许多船只已经开始使用LNG作为燃料．LNG燃料的加注方式通常为岸边加注，专用LNG加注船以其方便灵活、节省投资、极少占用码头资源等众多优势成为一个有很强竞争力的LNG产业装备选择[1]，但国内LNG加注船的研究尚处于起步阶段．由于加注船液舱会经常处于部分装载状态，晃荡问题是该船设计的一大难点，同时，晃荡荷载也是其围护系统的设计荷载之一[2]，而目前LNG加注船的液舱主要采用独立C型液舱，所以独立C型液舱的晃荡研究对于LNG加注船的设计与发展有着重大意义．

对于晃荡问题，国内外有很多学者对其进行了研究，其中模型试验由于成本较低且较为可靠，是主流的研究手段．Faltinsen等[3]运用解析法对不同形状液舱的晃荡进行了分析，并使用模型试验进行了验证，而且基于线性势流理论，通过解析的手段计算二维方形舱的晃荡荷载．Souto-Iglesias 等首先对晃荡的试验准备及晃荡数据的处理进行了介绍与讨论[4]；之后，通过对不同液舱宽度、不同试验介质(水和葵花籽油)的矩形液舱进行试验，系统地对晃荡荷载进行了研究，分析了液舱宽度增大引起的三维效应对冲击荷载的影响，并结合统计学的方法对试验结果进行了分析[5]．此外，针对试验中使用的介质与设备，Zou等[6]与卫志军等[7]分别就液体黏性与外激励设备对晃荡试验的影响进行了分析．前者利用羧甲基纤维素钠调节水的黏性，研究了试验介质黏性对冲击荷载的大小、产生及消退时间的影响；后者就单自由度晃荡平台及多自由度晃荡平台所产生的激励，通过冲击荷载的时程及特征值进行了比较分析．液体晃荡产生的自由液面形状，也是学者研究晃荡特性的热点．Olsen等[8]利用试验方法对横摇状态下液体的侧向冲击波形进行了系统的研究，并将其划分为5种不同类型，但其研究中包含的算例较少．Bouscasse等[9]对Olsen的研究进行了补充和拓展，包含了不同激励幅值、不同液位及激励频率的试验工况，从而发现并总结了第6种波形．Wei等[10]通过方形舱晃荡试验，补充了第7种晃荡波形，并给出了其发生幅值及频率范围．Jiang等[11-12]考虑液舱舱壁为弹性结构，通过扫频试验得到了液体产生最大荷载的试验低阶固有频率及液体冲击荷载，比较了弹性与非弹性液舱对固有频率及晃荡荷载的影响．

目前晃荡的研究主要针对方形及薄膜型液舱，而对于LNG独立C型液舱还很少见．本文以中海油能源发展服务有限公司的研究课题“1 000 m3LNG加注船液货系统国产化技术研究及试验”为背景，采用模型试验研究的方式，对1 000 m3LNG加注船的独立C型液舱进行了纵摇工况下，不同载液高度、激励频率及激励幅值的晃荡研究．讨论分析LNG独立C型液舱在纵向振荡时，其自由液面的波形特征，对较高液位下自由液面在舱顶的影响下出现的波形进行分类．此外，通过压力传感器的荷载采集，结合统计方法对晃荡荷载特性及其频域、空间分布情况进行研究．

1 模型试验系统

1.1 试验装置及试验方法

整个LNG独立C型液舱晃荡试验在船舶制造国家工程研究中心的实验室进行．试验系统主要由模型液舱、晃荡平台系统、晃荡荷载采集系统以及高速摄像机构成．

模型液舱由1 000 m3LNG加注船的实际液舱尺寸等比例变换而来，几何比例系数α=17.8，其外形完全仿照实际液舱的结构[13]，分成两侧的封头和中间的主罐体，主罐体由壁厚为10 mm的有机玻璃制成，封头由PVC材料制作而成．模型液舱总长(La)为1 890 mm，内直径(Di)为380 mm，长径比为4.97∶1．封头由标准椭圆封头构成，型号为EHA380×10PMMAJB/T4746[14]．试验选取水作为试验介质，并加入约5 mL的红墨水对介质染色，方便对自由液面形状的观察．为了采集、监测各载液高度下的晃荡荷载，在封头及液舱顶部设置监测点，以监测液体冲顶的荷载．具体荷载监测点的布置如图1所示．晃荡平台系统由六自由度晃荡平台与控制系统构成，平台最大承载质量为1 t，可模拟横摇、纵摇、艏摇、横荡、纵荡以及垂荡6个自由度的运动及它们的耦合运动，其具体参数如表1所示．晃荡荷载采集系统由齐平膜式压力传感器及欧姆龙(OMRON)公司生产的PLC(programmable logic controller，可编程逻辑控制器)采集模块共同构成，PLC采集模块可将压力传感器产生的电信号进行采集转换为数字信号，通过PLC专用输出数据采集软件PLC-ANALYZER pro 5读出内存地址中的数据，从而完成对压力信号的采集过程．压力传感器的量程为0～10 kPa，精度为0.2%FS．试验系统的运作图如图2所示．

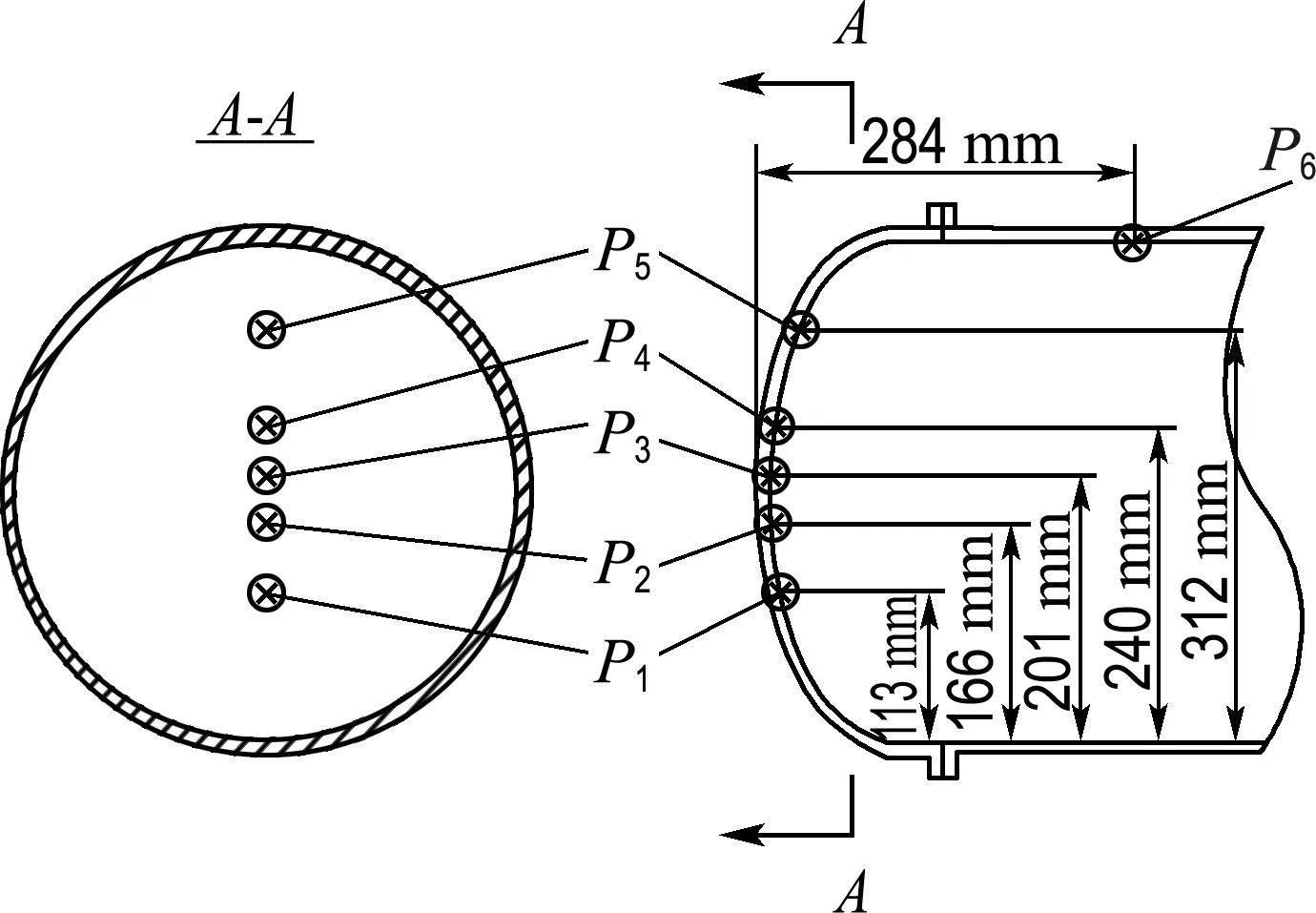
图1 压力监测点的布置

表1 六自由度晃荡平台运动性能参数

图2 晃荡试验系统运作图

1.2 试验工况

LNG独立C型液舱横向为圆形剖面，这种形状决定了其对横向的激励不敏感，而纵向的激励形式会使液体对舱壁产生较大的晃荡荷载；同时，在船舶航行中，纵摇是发生频率较高的船舶基本运动[15]，故本试验选取纵摇作为试验的主要外界激励形式．为了减少起振时晃荡状态的影响，采用变幅值的起振方式，其起振及激励方式如下式所示：

(1)

式中：y(t)为平台运动角度或位移，单位为°或mm；A为激励幅值，单位为°或mm；f为试验的激励频率，单位为Hz；t为试验进行时间，单位为s．可以看出，平台将通过20 s的起振时间到达给定的激励幅值运动状态．

当液舱内液体受到的外界激励频率与自身固有频率相接近时，液体会剧烈晃荡并对液舱产生较大的荷载，故试验的激励频率以液体纵向一阶理论固有频率(fn)为基点，以0.1fn为步长在一阶理论固有频率附近进行试验工况开展．载液工况以液舱内直径的比例并参考规范[2]选取，并根据载液高度与液舱长度之比，结合Faltinsen等[3]划分的液深标准对载液高度进行分类．同时配合1°～5°的纵摇激励幅值，最终具体试验工况如表2所示．

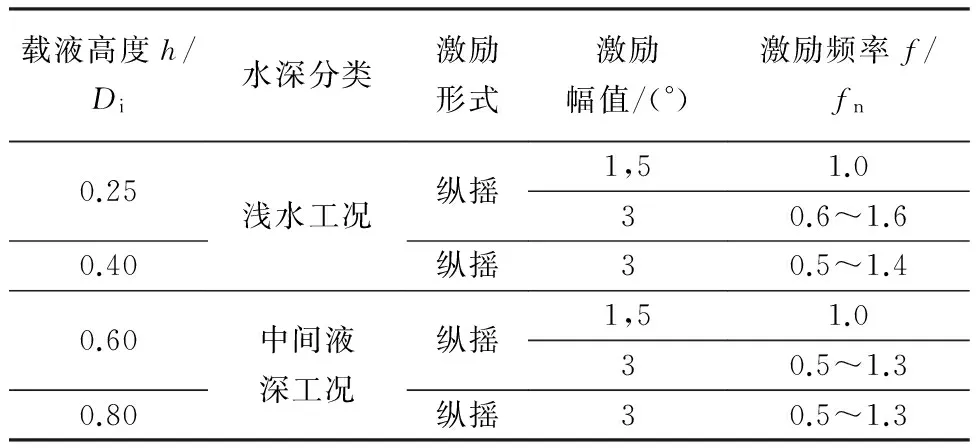
表2 试验工况

1.3 固有频率计算

利用试验系统对模型液舱内的液体，在纵向自由振荡的条件下，利用快速傅里叶变换对封头压力时程曲线进行频域变换，根据能量谱的最大峰值，可以得到液体纵向一阶理论固有频率．但由于试验工况中，0.80Di载液高度距离舱顶过小，导致舱顶对理论固有频率的分析有所影响，故采取数值方法的模态分析辅助理论固有频率的计算．

基于势流理论假设，通过有限元的离散方法，借助商业软件ADINA，对模型液舱内不同液位下的液体进行模态分析，求解一阶理论固有频率，根据模型液舱建立数值计算模型(如图3所示)．模型液舱舱壁的三向平移为约束条件，并加入重力加速度．将有机玻璃及PVC属性分别赋予液舱的主罐体及舱壁，将水的材料属性赋给势流体单元．使用行列式搜索法(determinant search)，对模型液舱的理论固有频率进行分析．计算结果与试验对比情况如表3所示，其中，fADINA为ADINA软件计算所得结果，fexp为试验测试所得结果．从结果的误差情况来看，数值计算在0.25Di、0.40Di及0.60Di的载液高度时，与试验值吻合情况很好，但在0.80Di载液高度时，相差较大，考虑到在该液位下的试验测量存在异常，故数值计算结果应为该液位下的一阶理论固有频率，最终选取试验工况的理论固有频率为表3中的fn．

图3 0.25Di载液高度下理论固有频率分析数值模型

表3 理论固有频率结果

2 试验结果与分析

2.1 晃荡波形特性

在文献[8]中，Olsen等将方形液舱内的浅水晃荡波形划分为5种形式：在低激励频率时，晃荡会表现出驻波形式；而当激励频率升高后，舱内液体会依次出现行波；之后变形为涌浪或者水跃，并在舱壁末端破碎；对于更高的激励频率，会使破碎后的波浪以涌浪的形式，行进于液舱中；继续提高激励频率，涌浪会最终变为孤立波．Lugni在激励周期为固有周期的0.75～1.65倍时，捕捉到了前4种类型的晃荡波形[3]．Bouscasse等[9]补充了第6种浅水晃荡波形，即当激励周期位于固有周期的0.5～0.6倍时，会形成一种完全非对称的波浪形态．之后，Wei等[10]发现了第7种晃荡波浪形态：当液体在0.37～0.50倍激励周期的作用下，幅值为舱长0.100～0.116倍时，在与侧壁作用后产生一个可以延伸至中横剖面的强烈卷碎浪．本文基于以上研究，应用其分类方法，对独立C型液舱中自由液面在晃荡时的形状进行探究．针对不同载液高度、激励频率及激励幅值，对液舱内晃荡波形分别论述．为了论述方便，规定罐体从平衡位置，逆时针向上运动为其运动的起始．

(1)0.25Di载液高度

当激励频率在0.6fn(0.13 Hz)至1.4fn(0.31 Hz)区间时，舱内液体主要表现为第3种波形，但由于封头为曲面，自由液面会沿封头翻卷落下后破碎．具体来说，在激励频率远离fn(0.22 Hz)时，液体会在液舱两端“堆积”(如图4(a)所示，其中，t为运动时间，T为激励周期)，几乎没有冲击力；在激励频率升高的过程中，自由液面沿封头上升幅度增大(如图4(b)所示)．在激励频率升至1.4fn(0.31 Hz)后，液体开始表现出第4种波形特征，即形成舱内往返运动的涌浪，且在封头翻卷后破碎(如图4(c)所示)，或形成水跃(如图4(d) 所示)．当激励频率到达1.6fn(0.35 Hz)后，舱内液体恢复驻波状态(第2种波形)，表明该液位一阶晃荡达到饱和(如图4(e)所示)．当载液高度不变，激励频率为fn(0.22 Hz)时，改变激励幅值为1°或5°后，液舱内的晃荡波形并无改变，仍旧维持第3种波形．

(2)0.40Di载液高度

液体在0.5fn(0.14 Hz)激励频率下，自由液面将呈现出第2种波形特征，升高至0.7fn(0.20 Hz)～0.9fn(0.25 Hz)时，自由液面将转变为第3种波形．若继续升高频率至fn(0.28 Hz)后，舱内将呈现出第4种波形状态，且自由液面将运动至封头顶端，沿主罐体顶部落下．随着激励频率的提高，自由液面将冲击封头顶端，液面破碎较严重(如图5(a)所示)．在激励频率达到1.3fn(0.36 Hz)后，波面呈现出第5种波形，即孤立波的形式，但兴起波高较小，并在冲击封头后破碎(如图5(b)所示)．当激励频率升至1.4fn(0.39 Hz)后，舱内液体将恢复至第2种波形，即在该液位，液体终止一阶晃荡(如图5(c)所示)．

(3)0.60Di载液高度

当载液高度达到0.60Di后，已超出了文献[8-10]中的水深工况，但当液体受0.5fn(0.18 Hz)及以下频率激励时，自由液面运动状态仍旧会与第1种波形状态一致；在激励频率为0.6fn(0.22 Hz)后，自由液面将以第2种波形状态上下起伏．而激励频率升至0.7fn(0.25 Hz)后，自由液面形状呈现出第3种波形状态，并在封头处有小部分波面的破碎(如图6(a)所示)．

但是，当激励频率升至0.8fn(0.29 Hz)～1.2fn(0.43 Hz)后，受舱顶的限制，此时自由液面的形状不再符合文献[8-10]中的波形描述方法，故本文扩充了中间液深工况的第2种冲顶波形(第1种冲顶波形会在之后介绍)，即液体会冲击封头顶部的过渡曲面，从而形成由液滴组成的高速射流(如图6(b)、(c)所示)，之后以涌浪的形式流向另一侧．并且随着激励频率的升高，射流长度加大，自由液面破碎点也会从封头顶部向主罐体顶部移动．当激励频率升至1.3fn(0.47 Hz)时，自由液面恢复为第2种波形状态，该液位一阶晃荡进入饱和状态．

图4 0.25Di载液高度下自由液面的变化

图5 0.40Di载液高度下自由液面的变化

图6 0.60Di载液高度下自由液面的变化

以fn(0.36 Hz)为激励频率，减小激励幅值为1°时，舱内液体将变为第5种波形，同样在冲击封头上端后自由液面破碎形成射流(如图7(a)所示)．而当幅值加大至5°时，舱内液体将会冲击舱顶，形成第2种冲顶波形，自由液面运动呈现较强的非线性，如图7(b)所示．

(4)0.80Di载液高度

液舱充装达到0.80Di载液高度时，冲顶现象频繁．0.5fn(0.24 Hz)激励时，会呈现出浅水工况中的第1种波形状态．在达到0.6fn(0.29 Hz)时，液体开始晃荡并表现出类似第2种波形状态，但与之不同的是，部分自由液面会“轻拍”舱顶，如图8(a)所示．当激励频率升至0.7fn(0.34 Hz)后，自由液面出现第1种冲顶波形，即液体在冲击封头顶部的过渡曲面形成射流后，沿主罐体顶部滑行至液舱中部(如图8(b)所示)．在激励频率处于0.9fn(0.43 Hz)～1.1fn(0.53 Hz)时，舱内晃荡液体会表现出第2种冲顶波形，并随着激励频率的加大，出现液体拍击罐体的响声，但自由液面冲击形成射流的位置更加靠近液舱中部(如图8(c)所示)．若继续升高激励频率至1.2fn(0.58 Hz)时，自由液面会恢复为第2种波形；而达到1.3fn(0.62 Hz)后，0.8Di载液高度下的一阶晃荡达到饱和．

图8 0.80Di载液高度下自由液面的变化

通过对试验现象中自由液面运动状态的分析，可以看出：

自由液面的运动会随激励频率不断靠近理论固有频率而变得剧烈，并在超出理论固有频率20%～30%后，才变得温和，而在浅水工况中，这个数值可以达到50%；这与Lugni发现的波形区间相一致．

浅水工况中，在0.25Di载液高度时，自由液面在冲击封头后，并没有引起较严重的破碎，在改变激励幅值时，波形仍无较大变化，整个液位一阶晃荡较温和；而0.40Di载液高度时，自由液面运动变得剧烈，在接近理论固有频率时会出现自由液面破碎的现象．

0.60Di载液高度时，自由液面运动会在低于0.8fn激励频率时，出现3种浅水波形，而当激励频率位于理论固有频率附近时，自由液面会表现出与文献中波形分类不一致的现象，即第2种冲顶波形．此外，在fn激励下，减小或增大激励幅值时并没有过多地改变液面破碎位置．

0.80Di载液高度时，液体将在较大范围的激励频率内，对主罐体顶部进行冲击，在低于理论固有频率时，液体表现出第1种冲顶波形，主要表现为自由液面在主罐体与封头顶部交界附近破碎，之后沿主罐体顶部运动；而在到达理论固有频率后形成第2种冲顶波形，其形成的射流速度更快，但之后不会沿主罐体顶部运动．

2.2 试验数据分析

(1)晃荡荷载特性

利用布置在封头处的监测点捕捉晃荡压力荷载，并加入平台输出的位移曲线，对晃荡荷载的变化趋势进行分析，可以发现，液体晃荡对液舱舱壁可产生两种类型的压力荷载时程，一种为单峰压力荷载曲线，一种为双峰压力荷载曲线．单峰曲线出现在0.25Di与0.40Di载液高度时，所有激励频率激励下的监测点；双峰曲线则只出现在0.60Di与0.80Di载液高度，并在理论固有频率附近的激励频率下．图9(a)、(b)分别为0.25Di载液高度与0.60Di载液高度的理论固有频率下，当晃荡达满幅值后自由液面处监测点的压力荷载．图中，为了更好地比较荷载与平台运动的关系，将晃荡荷载分别缩小至1/300与1/700．

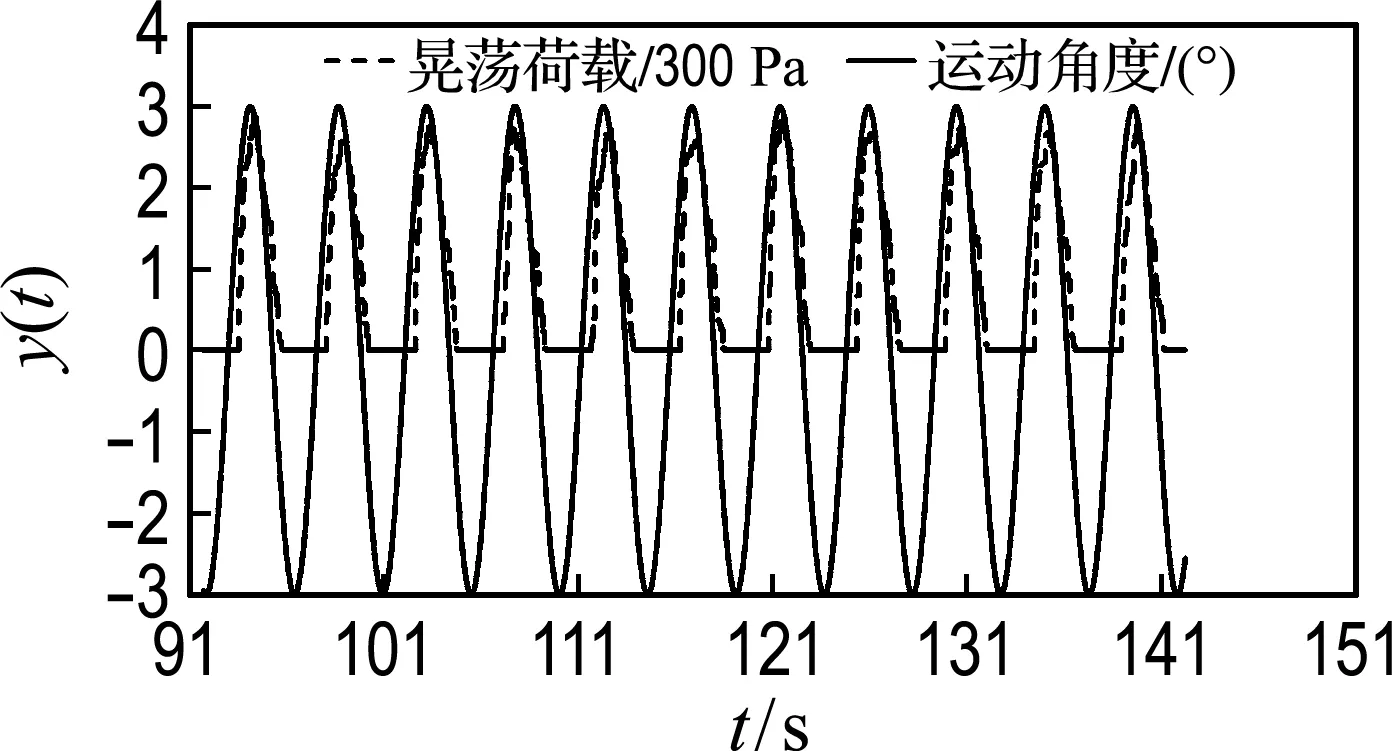
(a) 0.25Di载液高度(P1监测点)

(b) 0.60Di载液高度(P4监测点)

图9 理论固有频率下的晃荡压力荷载时程曲线

Fig.9 The pressure time history curve of sloshing load under theoretical natural frequency

由曲线图结合试验现象可知，单峰压力荷载曲线的峰值与双峰压力荷载曲线的第一次峰值，均发生在液舱运动至监测点一侧最低处时．从总体试验提取的荷载值来看，双峰压力荷载曲线出现于中间液深工况的高激励频率时，此时自由液面运动速度加快，当其运动至封头处时会冲击壁面，形成第1次峰值，之后液舱加速向水平位置运动，封头将会与受惯性作用的液体发生第2次碰撞，由于载液深度的加大与激励频率的提高，将再次形成一个持续时间较短的峰值．此观点可以被文献[16]所支持．而单峰压力荷载曲线发生的工况为浅水工况以及中间液深工况远离理论固有频率时，较少质量的液体与较低的激励频率导致其不会出现第2次荷载峰值．

(2)晃荡荷载的分布规律

由于晃荡荷载的随机性和离散性，本文使用统计值对晃荡荷载进行分析，分别提取试验数据中各不同工况下的全局最大值Pmax，其可以表示晃荡过程中出现过的最大荷载．此外，将不同工况荷载按从大到小排列，取前1/10数量荷载的平均值为1/10最大值P1/10，其可以表征在监测位置较大荷载的均值．因为在自由液面附近会出现较大的动荷载[17]，故选取各液位下自由液面处监测点的荷载进行数据分析．

分析各载液高度下的统计值的最大值，可以得到：在0.25Di载液高度下，产生全局最大值与1/10最大值的激励频率要比理论固有频率高出30%，而随着液位的升高，与理论固有频率的差值会随之减小(如图10所示)，在文献[5]和文献[12]中也提到了相同的趋势．当液位升至0.80Di载液高度时，两种统计值所对应的激励频率并不相等．这是因为液位的提高，使激励频率增长的幅度加大，过高的激励频率会使液体产生较大的瞬时动荷载，这一点可以从试验现象观察得出，故而产生全局最大荷载的激励频率仍旧高于理论固有频率；而激励频率在理论固有频率时，液舱运动速度有所下降，虽然没有出现较大的瞬时冲击动荷载，但液体对封头作用时间较较高激励频率时有所提高，导致了将较大荷载做平均后，产生最大值的激励频率会回落至理论固有频率下．

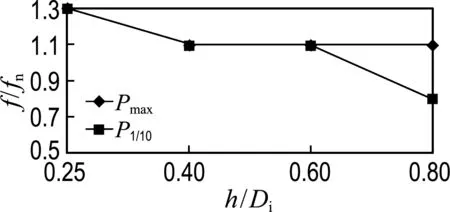
图10 荷载最大统计值与液位和激励频率的关系

Fig.10 The relationship of filling level and oscillation frequency with maximum statistical values of load

提取各液位的不同类型晃荡荷载的最大统计值(如图11所示)，可以发现，随着液位的升高，全局最大值和1/10最大值的晃荡荷载均不断增大，当增至0.60Di载液高度时达到最大值，之后荷载开始降低．这是因为在0.80Di载液高度下，自由液面破碎点移至液舱顶部，从而减弱了对封头处的冲击．结合试验现象中的自由液面变化情况，在对封头的结构设计时，应较多地关注0.60Di载液高度下的晃荡荷载．

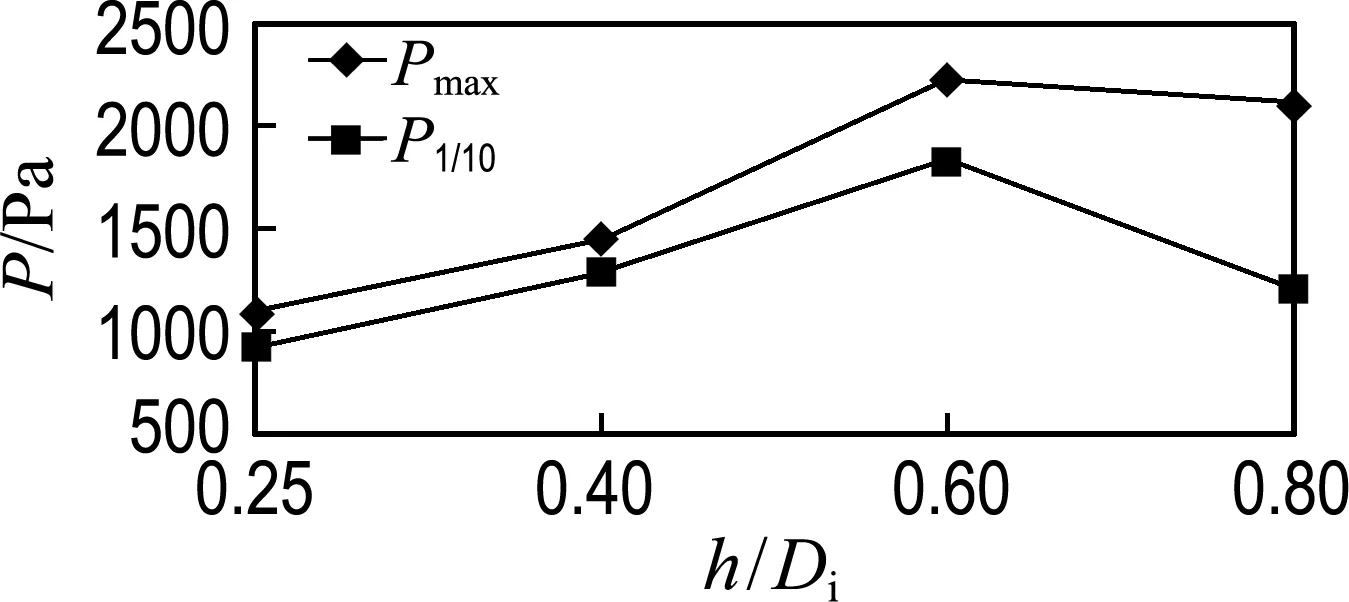
图11 各液位下的荷载最大统计值对比

针对0.60Di载液高度，提取自由液面及其附近的监测点P3、P4、P5，在不同激励频率下的全局最大值与1/10最大值(如图12所示)，可以发现，监测点在fn附近的频率激励下，全局最大值与1/10最大值的差值开始变大，并随监测点高度增加而增大，对应的激励频率均位于0.9fn(0.32 Hz)～1.2fn(0.43 Hz)，可以证明此时开始出现较大的冲击晃荡荷载，因而该激励频率区间下的晃荡对结构影响较大．

图12 晃荡荷载的统计值随激励频率的变化

针对0.80Di载液高度下，冲顶较为剧烈的情况，对P6监测点在不同激励频率下的全局最大值及1/10最大值进行分析(如图13所示)，当激励频率处于0.8fn(0.38 Hz)～1.2fn(0.58 Hz)时，顶部全局最大荷载已基本保持不变，证明此区间内主罐体顶部荷载相差不多，但会随着频率的升高而产生瞬时冲击荷载．因此，在此液位高度下，主罐体顶部的晃荡荷载是主要关注点，且产生较大冲顶荷载的激励区间为0.8fn～1.2fn．

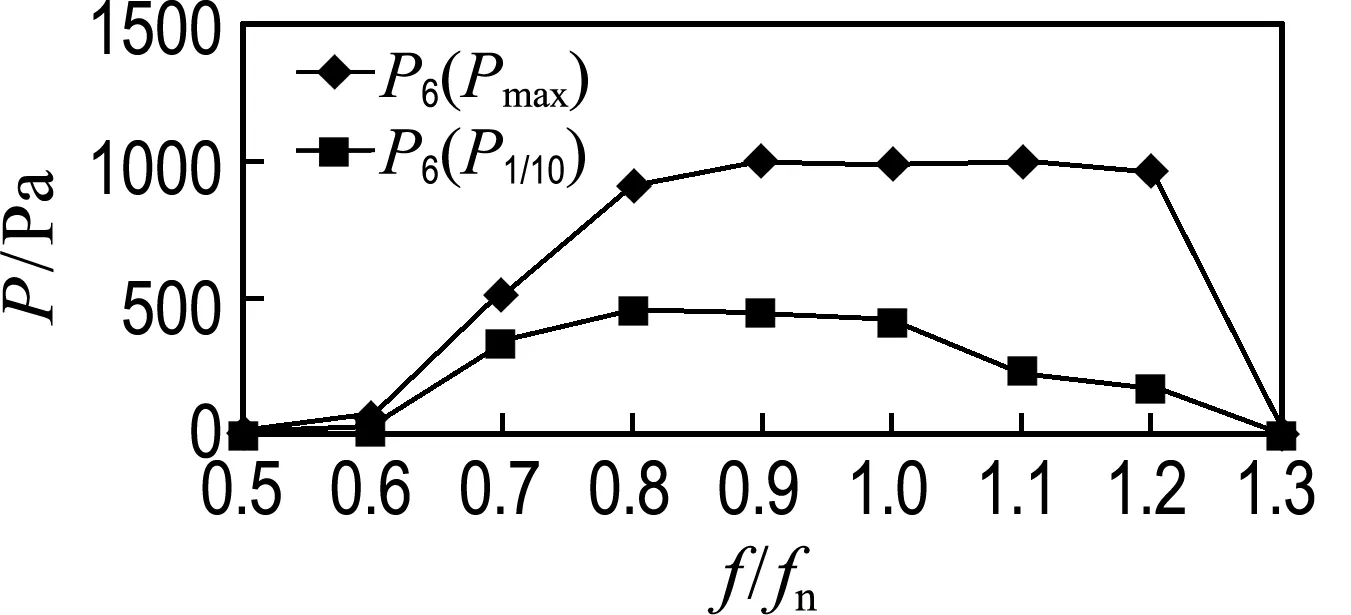
图13 冲顶荷载的统计值随激励频率的变化

3 结 论

(1)液舱内液体晃荡产生的自由液面，会随激励频率不断靠近理论固有频率而变得剧烈，但在超出理论固有频率20%～30%后，开始变得温和，而在0.25Di液载高度下，这个数值会达到50%．这是由于产生最大荷载的激励频率并不一定在一阶理论固有频率：在0.25Di载液高度下会升至1.3fn，而0.40Di、0.60Di、0.80Di载液高度下将会降低至1.1fn或1.0fn．

(2)0.25Di载液高度时，液体于理论固有频率附近晃荡时，其形成的自由液面在冲击封头后，并没有引起较严重的破碎，在改变激励幅值时，波形无较大变化，整个液位一阶晃荡较温和；当载液高度为0.40Di、0.60Di时，液体在理论固有频率及其附近的频率激励下，会沿封头冲击封头顶部的过渡曲面．在0.60Di载液高度下，自由液面冲击过后破碎较严重，同时，减小或增大激励幅值时并没有过多地改变液面破碎位置．故在液舱设计时，应注意此液位下封头上部及顶部过渡部分的晃荡荷载．

(3)0.80Di载液高度时，若低于理论固有频率，液体会表现出第1种冲顶波形，自由液面将在主罐体与封头顶部交界附近破碎，之后沿主罐体顶部运动；而在到达理论固有频率后形成第2种冲顶波形，与第1种冲顶波形的区别在于，液面破碎形成一道高速射流，但并不沿主罐体顶部运动．结合荷载的分析，对于液舱顶部结构的设计，应充分考虑0.8fn(0.38 Hz)～1.2fn(0.58 Hz)激励区间内的晃荡冲击荷载，并对舱顶结构做适当的加强．

本文对LNG独立C型液舱的晃荡进行了系统的试验研究，但晃荡荷载在封头与舱顶的具体空间分布情况未能给出，今后的研究中，会通过补充监测设备的试验方法或离散的数值方法进行深入研究．

[1] 杨 波,盛苏建,周 斌. 1 000 m3LNG燃料加注船总体布置设计[J]. 船海工程, 2014,43(5):138-141. YANG Bo, SHENG Sujian, ZHOU Bin. On general arrangement design of 1 000 m3LNG fuel bunker vessel [J].Ship&OceanEngineering, 2014,43(5):138-141. (in Chinese)

[2] 中国船级社. 液化天然气燃料加注船舶规范[S]. 北京:中国船级社, 2015.

China Classification Society. Rules for LNG Fuel Bunker Vessel [S]. Beijing: China Classification Society, 2015. (in Chinese)

[3] FALTINSEN O M, TIMOKHA A N.Sloshing[M]. Cambridge: Cambridge University Press, 2009.

[4] SOUTO-IGLESIAS A, BOTIA-VERA E, MARTIN A,etal. A set of canonical problems in sloshing. Part 0:Experimental setup and data processing [J].OceanEngineering, 2011,38(16):1823-1830.

[5] SOUTO-IGLESIAS A, BULIAN G, BOTIA-VERA E. A set of canonical problems in sloshing. Part 2: Influence of tank width on impact pressure statistics in regular forced angular motion [J].OceanEngineering, 2015,105:136-159.

[6] ZOU Changfang, WANG Deyu, CAI Zhonghua,etal. The effect of liquid viscosity on sloshing characteristics [J].JournalofMarineScienceandTechnology, 2015,20(4):765-775.

[7] 卫志军,陈晓东,董玉山,等. 两种运动平台下晃荡冲击荷载的实验研究[J]. 船舶力学, 2015(7):841-849.

WEI Zhijun, CHEN Xiaodong, DONG Yushan,etal. An experimental study of slamming impact load on two platforms [J].JournalofShipMechanics, 2015(7):841-849. (in Chinese)

[8] OLSEN H A, JOHNSEN K R.NonlinearSloshinginRectangularTanks:APilotStudyontheApplicabilityofAnalyticalModels[M]. Oslo: Det Norske Veritas, Research Department, 1975.

[9] BOUSCASSE B, ANTUONO M, COLAGROSSI A,etal. Numerical and experimental investigation of nonlinear shallow water sloshing [J].InternationalJournalofNonlinearSciencesandNumericalSimulation, 2013,14(2):123-138.

[10] WEI Zhijun, FALTINSEN O M, LUGNI C,etal. Sloshing-induced slamming in screen-equipped rectangular tanks in shallow-water conditions [J].PhysicsofFluids, 2015,27(3):032104.

[11] JIANG Meirong, REN Bing, WANG Guoyu,etal. Laboratory investigation of the hydroelastic effect on liquid sloshing in rectangular tanks [J].JournalofHydrodynamics, 2014,26(5):751-761.

[12] 蒋梅荣,任 冰,李小超,等. 有限液深下弹性侧壁液舱内晃荡共振特性实验研究[J]. 大连理工大学学报, 2014,54(5):558-567.

JIANG Meirong, REN Bing, LI Xiaochao,etal. Experimental study of resonant behavior of sloshing in elastic bulkhead tanks under finite depth [J].JournalofDalianUniversityofTechnology, 2014,54(5):558-567. (in Chinese)

[13] 管 官,林 焰,陈 明,等. 可变组合式C型LNG液舱晃荡模型试验装置及试验方法: ZL201410359571.4 [P]. 2016-07-13.

GUAN Guan, LIN Yan, CHEN Ming,etal. Experimental setup and method for modeling of sloshing in variable combination LNG C type tank: ZL201410359571.4 [P]. 2016-07-13. (in Chinese)

[14] 国家经济贸易委员会. 钢制压力容器用封头: JB/T 4746—2002 [S]. 昆明:云南科技出版社, 2002.

State Economic and Trade Commission. Formed Heads for Steel Pressure Vessels: JB/T 4746-2002 [S]. Kunming: Yunnan Science & Technology Press, 2002. (in Chinese)

[15] 王德禹,金咸定,李龙渊. 液舱流体晃荡的模型试验[J]. 上海交通大学学报, 1998,32(11):116-119.

WANG Deyu, JIN Xianding, LI Longyuan. On model experiment of sloshing in tanks [J].JournalofShanghaiJiaotongUniversity, 1998,32(11):116-119. (in Chinese)

[16] ZHAO Yucheng, CHEN H C. Numerical simulation of 3D sloshing flow in partially filled LNG tank using a coupled level-set and volume-of-fluid method [J].OceanEngineering, 2015,104:10-30.

[17] 卫志军,岳前进,阮诗伦,等. 矩形液舱晃荡冲击载荷的试验机理研究[J]. 船舶力学, 2012(8):885-892. WEI Zhijun, YUE Qianjin, RUAN Shilun,etal. An experimental investigation of liquid sloshing impact load on a rectangular tank [J].JournalofShipMechanics, 2012(8):885-892. (in Chinese)

ExperimentalstudyofsloshingpatternonLNGindependentCtypetank

LIU Ge1, LIN Yan*1,2, GUAN Guan1, LI Bing1

( 1.School of Naval Architecture & Ocean Engineering, Dalian University of Technology, Dalian 116024, China； 2.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China )

Being different from the LNG carrying ship, the tanks of LNG fuel bunker vessel are always partially loaded, so the sloshing must be considered. Since independent C type tank is widely used in LNG fuel bunker vessel at present, model experiments with this type of tank are carried out for sloshing research. The test conditions cover different filling levels, excitation frequencies and excitation amplitudes. The characteristic of free surface shape is discussed and analyzed. Furthermore, in the intermediate depth, classification of wave shapes, which is influenced by tank roof, is identified. With the statistical analysis of sloshing load, it is found that there is deviation between the excitation frequency inducing maximum load and theoretical natural frequency. This deviation will reduce as the filling level increases. In addition, on aspect of spatial distribution of sloshing load, the free surface under 0.6Di(Diis the diameter of the model tank) filling level strongly breaks up and large impact pressure will be expected at upper part head; under 0.8Difilling level the roof impact pressure with the excitation frequency between 0.8fn(fnis theoretical natural frequency) and 1.2fnshould be taken full account.

sloshing; independent C type tank; LNG fuel bunker vessel; experimental study

2017-01-19；

2017-07-14．

工业和信息化部高技术船舶科研计划资助项目(工信部联装[2014]498号)；海洋可再生能源专项资金资助项目(QDME2013ZB01)；国家自然科学基金资助项目(51609036)；中国博士后科学基金资助项目(2014M561234，2015T80256)；辽宁省博士科研启动基金资助项目(201501176)；中央高校基本科研业务费专项资金资助项目(DUT16RC(4)26).

刘 戈(1987-)，男，博士生，E-mail:brant1987799@sina.com；林 焰*(1963-)，男，教授，博士生导师，E-mail:linyanly@dlut.edu.cn.

1000-8608(2017)05-0467-09

U661.73

A

10.7511/dllgxb201705005