角加速度计在飞行器/水下航行器制导控制系统中的应用

, ,

(1.北京机电工程研究所,北京 100074；2.北京自动化控制设备研究所,北京 100074)

角加速度计在飞行器/水下航行器制导控制系统中的应用

陈峣1,全胜1,邓继权2

(1.北京机电工程研究所,北京100074；2.北京自动化控制设备研究所,北京100074)

介绍了角加速度计在飞行器/水下航行器制导控制的三个领域:制导控制一体化设计、抗未知瞬发干扰稳定控制、动力学系数辨识中的应用机理。角加速度计作为一种测量用传感器,能够在飞行器/水下航行器运动过程中直接采集俯仰、航向和滚动三个通道的飞行器/航行器本体的角加速度信息。通过对角加速度信息的获取及处理,分析飞行器/水下航行器质心运动与姿态运动的内在联系,同时将角加速度信息与惯性导航转置所采集的信息相互结合,便可以使得系统的动力学系数辨识和制导控制一体化设计成为可能;同时,由于角加速度信息在相位上超前于角速度反馈,因此引入角加速度信息的反馈可以提升飞行器/水下航行器抗未知瞬发干扰的能力。

角加速度计;制导控制一体化;稳定控制;动力学系数辨识

0 引言

角加速度是角位移对时间的二次微分,也可以是角速度对时间的一次微分。角加速度计是一种测量角加速度的惯性传感器,它在汽车、航空航天、电子等领域具有广泛的应用。在惯性传感器中,与角加速度计相比,线加速度计和角速度陀螺得到人们更大的关注。然而角加速度计的用途也十分广泛,具有线加速度计和陀螺不可替代的作用[1]。

在角加速度计(以下简称角加)所测量飞行器/水下航行器滚动通道、航向通道、俯仰通道的弹体角加速度信息中,航向通道、俯仰通道弹体角加速度信息还分别包含了弹体航向过载、俯仰过载的微分信息。在水平飞行/航行的状态下,弹体航向过载、俯仰过载微分与角加速度的关系可近似为

(1)

(2)

式(1)、式(2)描述了飞行器/水下航行器航向通道、俯仰通道质心运动与姿态运动的内在联系,使得航向通道、俯仰通道质心控制、姿态控制一体化设计成为可能。

引入角加速度反馈,也就是引入了干扰力矩反馈,在相位上90°超前于现有的角速度反馈。因此,飞行器/水下航行器滚动稳定控制引入角加速度反馈后,将提升抗未知瞬发干扰能力。

综合惯导、角加观测信息,可获得飞行器/水下航行器六自由度的全部一阶、二阶状态分量,即质心速度与线加速度、绕质心角速度与角加速度。据此,可以在线、离线辨识出飞行器/水下航行器动力学参数。

下面将逐一介绍角加在制导控制一体化设计、抗未知瞬发干扰稳定控制、动力学系数辨识中的应用机理。

1 角加速度计在制导控制一体化设计中的应用

传统的飞行器/水下航行器制导与控制系统设计是将制导回路和控制回路分开设计的[2]。由于制导律的设计只考虑中制导质心运动、末制导弹目相对运动关系,控制系统的设计只考虑弹体动力学方程,没有考虑制导回路和控制回路动力学之间的联系,导致制导与控制缺乏有机协调与匹配,同时飞行器/水下航行器的机动能力也得不到充分的发挥。制导控制一体化方法将传统的制导回路和控制回路作为一个整体来研究,同时利用飞行器/水下航行器所有可测量状态信息,能更好地发挥飞行器/水下航行器的机动能力,获得更优异的制导性能。

本文在文献[3]、文献[4]中提出的二阶非线性滑模面函数基础上,提出了一种高阶(三阶、四阶)非线性滑模面函数,来实现基于角加速度信息反馈的制导控制一体化设计。

三阶滑模面函数的一般表达式为

(3)

四阶滑模面函数的一般表达式

(4)

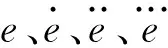
下面将依据四阶滑模面函数设计飞行器/水下航行器中制导控制一体化控制律,依据三阶滑模面函数设计末制导阶段制导控制一体化控制律。

1.1 飞行器/水下航行器制导控制一体化控制律

本节以某水下超空泡航行器[5-6]的深度控制为例,介绍角加在中制导控制一体化设计中的应用。

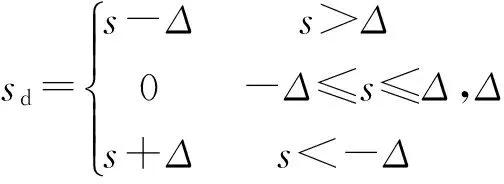
(5)

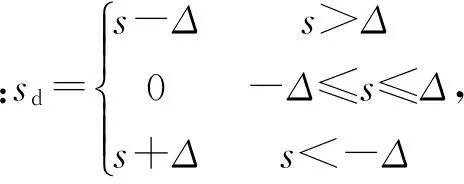
Δ为死区宽度。

开关控制量为

(6)

其中,du为常值开关量控制量;k1、k2、k3、k4为控制参数;ε为正的小常数,根据实际设计经验,一般取做0.02。

舵控电压为

u=us+kp·e+kα·α

(7)

其中,kp、kα为控制参数,α=ωzb/(s+a4),ωzb为弹体俯仰角速度,s为拉氏算子,1/a4为纵向机动时间常数。

上述一体化控制设计以及现有的深度控制与姿态控制分立设计的某水下超空泡航行器的数学仿真对比如图1所示。相对于采用PID控制方法的分立控制设计下的深度(红色曲线),采用滑膜控制方法(SVC)设计的一体化控制下的深度(蓝色曲线)更快、近似无超调地过渡到定深值。

图1 一体化控制(蓝线)与独立控制(红线)下的航行器深度变化曲线Fig.1 Integration/Independant control curve of the craft’s depth variation

1.2 飞行器/水下航行器末制导控制一体化控制律

仍然以某水下超空泡航行器航向导引控制为例[7-8],介绍角加在末制导段制导控制一体化设计中的应用。

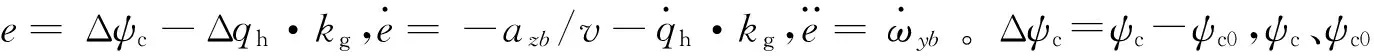
(8)

同样对s作死区处理:

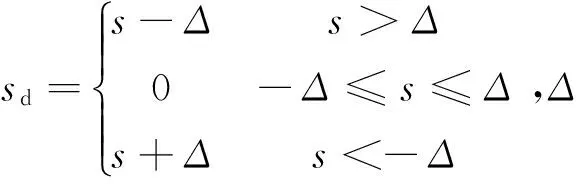
开关控制量为

(9)

其中,du为常值开关量控制量;k1、k2、k3为控制参数;ε为正小常数,依据实际设计经验,一般取0.02。

舵控电压为

u=us+kp·e+kβ·β

(10)

其中,kp、kβ为控制参数,β=ωyb/(s+b4),ωyb为弹体航向角速度,s为拉氏算子,1/b4为航向机动时间常数。

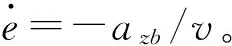
图2 末制导控制下的弹道偏角(红线)、弹目线方位角(蓝线)Fig.2 Trajectory deflection angle and azimuth of bullet line of terminal guidance control

单独观察末端制导曲线,如图3所示。

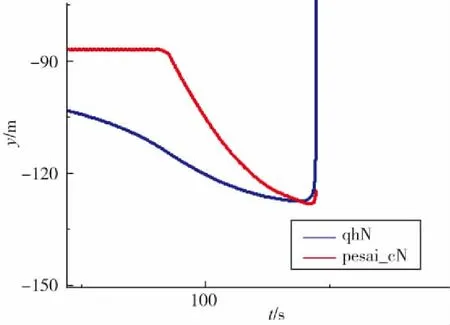
图3 末段的弹道偏角(红线)、弹目线方位角(蓝线)Fig.3 Trajectory deflection angle and azimuth of bullet line of terminal

一体化导引控制下的航行器速度轴快速转向、接近弹目线,在到达目标前追上弹目线,实现了较小的末制导偏差。

2 角加速度计在稳定控制中的应用

飞行器/水下航行器的滚动通道易受航向通道、俯仰通道交联耦合干扰[9]。常规的滚动角PID控制通过滚动角速度反馈来感知滚动姿态变化趋势,因此滞后于干扰力矩90°相位。引入滚动角加速度后,直接感知干扰力矩。下面介绍角加在抗干扰稳定控制中的应用。

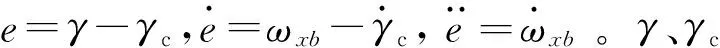
(11)

对s作死区处理:

开关控制量为

(12)

其中,du为常值开关量控制量;k1、k2、k3为控制参数;ε为小正常数,一般取0.02。

舵控电压为

u=us+kp·e

(13)

其中,kp为控制参数。

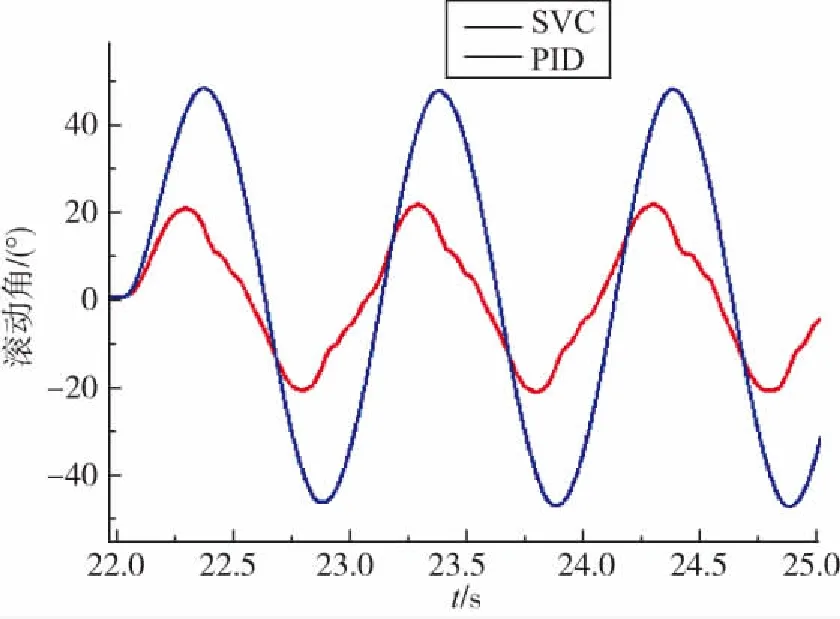
图4 两种稳定控制下的滚动角曲线Fig.4 Curve of roll angle of two stability control methods

引入角加稳定控制与常规PID稳定控制的抗瞬发正弦变化干扰仿真对比如图4所示。其中,红色曲线为引入了角加稳定控制的滚动角曲线,蓝色曲线为常规的PID稳定控制的滚动角曲线。相对采用PID方法设计的稳定控制,采用滑膜控制方法(SVC)设计的角加稳定控制下的滚动角误差幅值减小一半。

3 角加速度计在飞行器/水下航行器动力学系数辨识中的应用

一般而言,飞行器/水下航行器三通道小扰动动力学方程组为[10]:

俯仰通道:

a1·ωzb+a2·α+a3·δz=Mzb

(14)

航向通道:

b1·ωyb+b2·β+b3·δy=Myb

(15)

滚动通道:

c1·ωxb+c2·β+c3·δx=Mxb

(16)

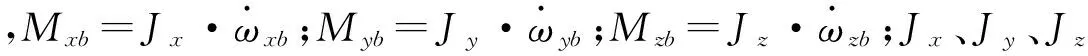
对一般的未采用角加的系统来说,由于无法得到精确的角加速度的数值,因此上述3个方程的右侧均为未知量,无法通过求解方程组的形式,对系统的动力学系数进行辨识;即使通过角速度微分求得了角加速度信息(一般称之为“软角加”),也往往存在很大的计算误差而使得结算得出的系统的动力学辨识系数带有很大的偏差。

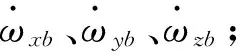
然后利用递推最小二乘参数辨识法,可以在线辨识出动力学系数;利用极大似然参数辨识法,可以离线辨识出动力学系数。

4 结论

本文介绍了角加在飞行器/水下航行器制导控制一体化设计、抗未知瞬发干扰稳定控制、动力学系数辨识中的应用机理。通过构建更高阶的滑膜面函数(包含角加速度信息),使得飞行器/水下航行器中制导段和末制导段的制导控制一体化设计成为可能,通过仿真也验证了这种设计的优越性;其中,通过引入超前于角速度反馈相位90°的角加速度信息,系统具有了更加优越的抵抗未知瞬发干扰的能力;最后,引入角加速度信息的反馈,使得在线/离线辨识飞行器的动力学参数成为可能。可以预见的是,随着飞行器/水下航行器制导控制系统技术的发展,角加应用将得到推广、深化。

[1] 吴校生,陈文元.角加速度计发展综述[J].中国惯性技术学报, 2007,15(4):458-463.

[2] 孟秀云.导弹制导与控制系统原理[M].北京: 北京理工大学出版社, 2003.

[3] 卿立.一种变结构控制方案自动驾驶仪的研究[J].战术导弹控制技术, 2001(2): 7-11.

[4] 刘金琨,孙富春.滑膜变结构控制理论及其算法研究和进展[J].控制理论与应用.2007,24(3):407-418.

[5] Recchi S, Hensler G.The refill of superbable cavities[J].Journal of Astronomy and Astrophysics, 2008,2(6):53-58.

[6] Lee Q, Xue L, He Y.Experimental study of ventilated supercavities with a dynamic pitching model[J].Journal of Hydrodynamics, 2008,20(4):456-460.

[7] Zou W, Liu H.Control of the ventilated supercavity on the maneuvering trajectory[J].Journal of Ocean Engineering, 2015,101(1):235-243.

[8] Liu M, An W, An H.Dynamic reliability analysis of supercavity vehicle with stochastic parameters under impact loads[J].Journal of Harbin Institute of Technology, 2012,19(3):111-113.

[9] 陈海涛,沈欢.基于辅助决策方法的低空飞行器干扰技术[J].科技通报，2012,28(6):119-121.

[10] 方振平.飞机飞行动力学[M].北京: 北京航空航天大学出版社, 2005.

TheApplicationofAngularAccelerometerintheGuidanceandControlSystemofAirVehicle/UnderwaterVehicle

CHENYao1,QUANSheng1,DENGJi-quan2

(1.BeijingMechanicalandElectricalEngineeringResearchInstitute,Beijing100074,China；2.BeijingInstituteofAutomaticControlEquipment,Beijing100074,China)

This article introduces the application of the angular accelerometer in the guidance and control system of air/underwater vehicle in three aspects: guidance and control integration, resistance to unknown and instant interference and dynamic coefficient identification.As a measuring sensor, angular accelerometer can directly collect the angular acceleration of pitch, yaw and roll channels of the air/underwater vehicle during the motion.It is possible to identify the dynamic coefficient and design the guidance and control integration system by gathering and disposing the information of the angular accelerometer and analyzing internal relationship between centroid motion and attitude motion of the air/underwater vehicle.Meanwhile, because the angular acceleration is leading the angular velocity on phase, it is possible to enhance the ability of the system to resist to the unknown instant interference by introducing the information of the angular accelerometer.

Angular accelerometer; Guidance and control integration; Stability control; Dynamic coefficient identification

2017-04-22；

：2017-06-20

：国家自然科学基金创新研究群体项目(61021002)

：陈峣(1986-)，男，硕士，工程师，主要从事导航制导与控制系统方面的研究。E-mail:chenyao0001@126.com

10.19306/j.cnki.2095-8110.2017.05.010

TP273

：A

：2095-8110(2017)05-0060-05