微弱GPS信号避开比特跳变的捕获算法

, ,

(北京航空航天大学,北京 100191)

微弱GPS信号避开比特跳变的捕获算法

程燕,常青,李显旭

(北京航空航天大学,北京100191)

为了提高全球定位系统(Global Positioning System，GPS)接收机的灵敏度,信号捕获过程需要加长积分时间。分析了比特跳变对加长相干积分时间的限制,从而提出一种能够完全避免比特符号跳变的捕获算法。该算法通过对多组数据采用相干积分和非相干积分相结合的方法,比较各组积分结果并选取积分最大值,用来判决是否捕获。算法中相干积分时间为19ms,目的是使积分最大值组完全避开数据位跳变,避免导航数据符号跳变对相干积分值的影响。该算法在避开比特跳变的基础上最大程度地提高相干积分时间,提高GPS接收机的捕获灵敏度。仿真结果表明,该算法能有效地捕获到载噪比(Carrier to Noise Rate,CNR)低至26dB·Hz的信号,可有效提高GPS接收机的捕获灵敏度。

相干积分;比特符号跳变;非相干积分;高灵敏度

0 引言

在全球导航卫星系统(Global Navigation Satellite System,GNSS)接收机中,捕获是信号处理的第一个关键环节。接收机在开始信号跟踪之前,需要首先估算出接收信号的载波频率和码相位这2个参数。然后根据这些估计值初始化跟踪环路,来帮助接收通道展开对信号的跟踪,而信号捕获的目的正是为了获取所有可见卫星信号的载波频率和码相位的粗略估计值[1]。

然而,在实际环境下,GNSS接收机广泛应用于弱信号环境下,例如:室内、森林遮挡等,这些环境下卫星信号的载噪比(Carrier to Noise Rate,CNR)比在户外开放环境下信号的载噪比低20dB左右[2]。传统的捕获算法很难捕获到该弱信号,因此,这就要求我们提高软件接收机对弱信号捕获的灵敏度[3]。

一般提高灵敏度的弱信号捕获算法是延长积分时间。相干积分、非相干积分和差分非相干积分是常用的弱信号累积方法[4]。根据最大似然准则,延长相干积分时间是提高捕获灵敏度最有效的方法。但是导航数据位的符号跳变,限制了相干积分时间。GPS的导航电文数据速率为50bit/s,即每20ms都有可能发生比特符号跳变[5],在比特起始位置未知时,相干积分时间不能超过20ms。

为了捕获弱信号,半比特算法[6]通常应用于GPS L1 C/A码弱信号捕获中,该算法相干积分时间为10ms,由于相邻两组10ms数据最多只有一组存在比特翻转,将接收信号分成10ms为一段的数据块,并对奇偶块分别进行非相干积分,比较奇偶块的非相干积分值,将较大的积分值与捕获门限相比较,并判决是否捕获。

文献[7]提出全比特算法,将相干积分时间延长至20ms。首先在20ms数据块内用相干积分,然后不同20ms数据块之间用非相干积分。由于数据比特符号翻转的位置未知,要在每个可能的比特位置开始积分,这样会形成20组结果。非相干积分最大值组就代表与导航数据比特近似同步情况下的积分值。

半比特算法能有效避开导航数据位翻转的影响,但是相干积分时间只有10ms,不利于提高捕获灵敏度。全比特算法粗略的估计比特符号翻转的位置,只能确定比特翻转的位置在非相干积分值最大组起始的1ms之内,但不能确定1ms内的具体位置。因此,对于该20ms内的相干积分仍可能存在正负抵消,从而使得该20ms数据块的相干积分值被衰减,由周期性可知,随后连续的信号中每20ms数据块的相干积分值都有可能受到跳变而引起衰减,从而降低了信噪比。

针对以上算法的优缺点,本文提出一种避开比特跳变的算法,算法中相干积分时间为19ms,在完全避开比特跳变的基础上,充分延长了相干积分时间,提高了捕获灵敏度。

1 信号模型和数据位跳变

1.1 GPS L1 C/A信号模型

GPS卫星信号经过接收模块,降频、采样和量化后,转化为中频数字信号,接收机信号处理部分都是从数字中频信号开始的。接收机收到的中频信号模型[8]为

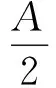
w(n)

(1)

其中,A是信号幅度,d(n)代表电文速率为50Hz的导航数据信号,c(n)为C/A码,码长为1023chips,码速率为1.023MHz。fIF为中频频率,fd为多普勒频移,τ是码时延,φ0是初始相位,w(n)是均值为0,方差为σ2的加性高斯白噪声。Ts=1/fs,fs为采样频率。

捕获系统一般是基于处理接收信号和本地信号相关得到的互模糊函数(Cross Ambiguity Function,CAF),互模糊函数可定义为

(2)

由于串行搜索方法相关运算的计算量大,为了减少捕获时间,通常将时域相关运算转化为频域相乘,采用并行频域搜索算法[9]。

互模糊函数可以通过并行搜索的捕获方法式(3)得到。

(3)

1.2 数据位跳变的影响

在计算互模糊函数时,假设导航数据符号在相干积分期间是不变的。但是,在没有辅助信息时,一个C/A码周期内,数据位符号是有可能跳变的。

当导航数据符号跳变时,d(nTs)变为双脉冲信号,如图1[10]所示,Nτ是用离散时间符号表示的码延迟。

图1 数据位

在不考虑噪声的情况下,对接收信号和本地复制信号进行一个C/A码周期的相干积分,并且在多普勒频移和码延迟都是对齐时,互模糊函数的包络随着比特符号变化的位置而变,如式(4)所示,对应图如图2所示。

S(τ,fd)=Nτ-(N-Nτ)

(4)

式中,S(τ,fd)为互模糊函数的包络,N为在相干积分时间为一个C/A码周期时,没有数据位跳变时的互模糊函数的包络峰值。Nτ是用离散时间符号表示的码延迟。

从图2[8]可以看出,当数据位翻转发生在码周期的中间时,互模糊函数的包络峰值会消失。考虑到噪声和多径信号,当数据符号跳变接近C/A码周期中间时,接收机很有可能捕获不到正确的多普勒频移和码延迟。

图2 数据位翻转不同位置时互模糊函数包络Fig.2 CAF envelop at different bit transition location

2 传统高灵敏捕获算法及其问题

2.1 半比特算法

半比特方法需要计算2个非相干积分量。从观测区间内中频信号中任取一点作为处理数据的起始点,把后面的接收数据划成2N(N为整数)个持续时间为10ms的相干积分区间块,把每10ms的数据块都进行相干积分,相干积分结果记为:Ym(m=1,2,3,…,2N)。然后把奇数块和偶数块的相干积分值分别进行非相干累加,如式(5)所示。

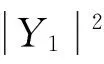
(5)

最后将Y=max(Ysum1,Ysum2)作为最终捕获判决量。这种处理方式,可以保证其中至少有一组非相干积分值不受导航数据跳变的影响。

2.2 全比特算法

半比特算法的有效相干积分时间为10ms,为了进一步延长相干积分时间,可以将相干积分时间延长至20ms,即全比特算法。

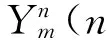
(6)

其中,n为组数,n=1,2,3,…,20。

图3 全比特算法原理图Fig.3 Schematic diagram of the full-bits algorithm

取Y=max(Y1,Y2,…,Y20)作为判决量与门限比较完成捕获。

2.3 传统算法存在的问题

半比特算法能够避免数据位的跳变,但是对20ms的数据进行处理,有效的相干积分时间只有10ms,相干积分时间较短,不利于捕获较弱的信号。

全比特算法将相干积分时间延长至20ms,并将数据分成20组,每组分别进行非相干积分,目的是估计出数据位跳变的大致位置。但是该算法只能确定跳变位置在最大非相干积分组的第1个1ms内的某一点。如图3所示,假设第2组为积分最大值组,即Y=max(Y1,Y2,…,Y20)=Y2,则可知,数据位跳变位置在第2组中数据块1的第1个1ms内的某个数据采样点,若采样频率fs为124MHz,则1ms内的采样点数为fs/1000=124000,即数据位跳变的位置在第2组第1个1ms内的124000中的某个采样点上。由于导航数据比特周期为20ms,随后每个数据块中的第1个1ms内均有可能存在跳变。也就是说,每个20ms的数据块相干积分期间仍然有可能存在数据位跳变,数据块内的相干积分值仍然存在正负抵消问题,互模糊函数的幅值会因此受到衰减。假设数据位跳变由负跳为正,虽然负数部分持续时间不到1ms,但是若负数部分相干积分值较大时,当其与数据块内正数部分相干积分值相加,会大大衰减正数部分相干积分值,从而大大影响本数据块最后的相干积分值。

因此,全比特算法只是大致估计了数据位跳变的位置,仍然没有避免数据位跳变对相干积分值的影响。当数据位跳变频繁时,假设导航数据为010101……,而且算法处理的数据起始点并不在数据跳变的边沿时,此时全比特算法算出的最大非相干积分值Y,受跳变影响很大,且会影响相关峰值,从而降低信噪比。

3 避开比特跳变的捕获算法

3.1 改进算法原理

为了完全避开数据位跳变的影响,本文提出一种相干积分时间为19ms的捕获算法,该算法能够完全避免数据位跳变的影响,提高信噪比。

(7)

取Y=max(Y1,Y2,…,Y20)与判决门限相比,判断是否能够捕获。

图4 避开比特跳变算法的原理图Fig.4 Schematic diagram of the avoiding bit transition algorithm

该算法根据非相干积分最大值可估计出数据位跳变大致位置,但是为了完全避开数据位跳变,每个数据块的最后1ms不参与相干积分计算。这样可以保证积分最大值组完全不包含数据位的跳变,完全避开数据位跳变对相干积分值的削弱,从而提高捕获的灵敏度。

3.2 改进算法流程

该算法具体流程描述如下:

1)数据段的选择。任选一点作为数据段的起点,从此点后选取每20ms为一个数据块,共选择M个数据块作为第1组数据,其余19组依次延迟1ms。

2)计算相干积分和非相干积分。处理每一组数据时,对每一个数据块中的前19ms进行相干积分,每个数据块中的最后1ms不进行处理,然后对M个数据块的积分结果进行非相干累加,如式(7)所示。

3)求非相干积分最大值并进行判决。求20组非相干积分值的最大值Y=max(Y1,Y2,…,Y20),并与设定好的捕获门限A进行比较。若Y≥A,则捕获成功,积分最大值组的数据完全不含导航数据位的跳变;反之,则捕获失败。

4 仿真分析

为了验证本文算法的可行性,在Matlab环境下对其进行仿真。

仿真产生的中频信号为40.098MHz,采样频率为124MHz。

将该算法与半比特算法进行相比,对于载噪比CNR=29dB·Hz的信号,在处理信号长度为80ms时,本算法和半比特算法仿真结果对比如图5所示。

(a) 改进算法 (a) Improved algorithm

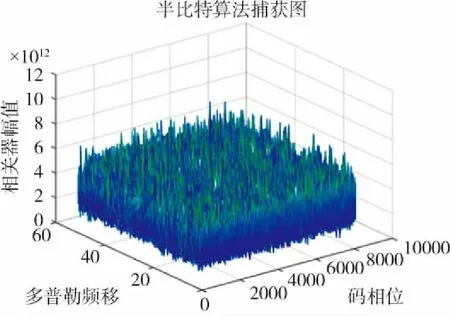
(b) 半比特算法(b) Half-bits algorithm图5 改进算法与半比特捕获图比较Fig.5 Comparison of the improved algorithm and the half-bits algorithm

图5中改进算法有明显的峰值,噪底较小,能够正常捕获；但是半比特算法峰值不明显,噪声很大,不能正确捕获信号。对于半比特算法,加长信号的长度,就能捕获到载噪比CNR=29dB·Hz的信号。

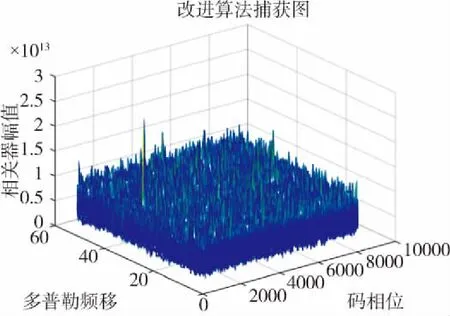
对于载噪比为26dB·Hz的信号,半比特算法已经不能捕获,但是本文算法仍然能够捕获,此时采用的信号长度为120ms,捕获图如图6所示。从图6中可以看出,CNR降到26dB·Hz时,相对于CNR=29dB·Hz,噪底有所增加,但是峰值仍然很突出,能够正常捕获。

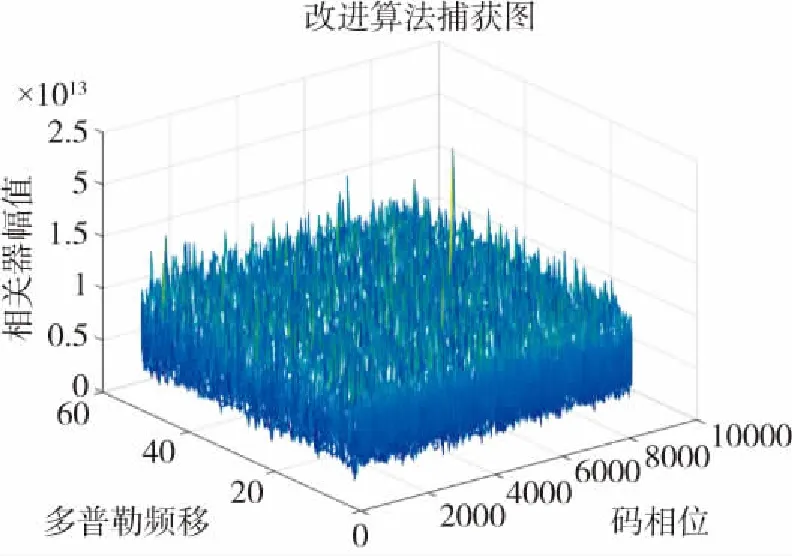
图6 改进算法,CNR=26dB·HzFig.6 Improved algorithm, CNR=26dB·Hz

通过仿真可知,本文提出的算法能够捕获载噪比为26dB·Hz的信号,而半比特算法只能捕获到29dB·Hz的信号。在处理相同时间长度的信号时,本文算法出现的峰值很明显,峰值幅度较大,表现出明显的优势,而半比特算法峰值不明显,不能正确捕获。因此,本文算法可提高检测概率,提高捕获灵敏度。

5 结论

本文分析了比特跳变和传统弱信号捕获算法存在的问题,并提出了完全避开比特跳变的算法,该算法将相干积分时间延长至19ms,在完全避开比特跳变的基础上,最大程度地延长了积分时间。通过与传统弱信号捕获算法仿真对比显示,该算法提高了检测概率,并且能够捕获载噪比低至26dB·Hz的信号,提高了软件接收机的捕获灵敏度。

[1] 谢钢.GPS原理与接收机设计[M].北京: 电子工业出版社，2009:349.

[2] Macgougan G D.High sensitivity GPS performance analysis in degraded signal environments[J].Geomatics Engineering University of Calgary, 2003.

[3] Subburaj K, Bhatara S, Tangudu J, et al.Spurmitigation in high-sensitivity GNSS receivers[J].IEEE Transactions on Circuits & Systems II Express Briefs, 2014, 61(2):100-104.

[4] Borio D, Akos D.Noncoherent integrations for GNSS detection: analysis and comparisons[J].IEEE Transactions on Aerospace & Electronic Systems, 2009, 45(1):360-375.

[5] Akos D M, Normark P L, Lee J T, et al.Lowpower Global Navigation Satellite System (GNSS) signal detection and processing[C]//Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, 2000:784-791.

[6] Lin D M, Tsui J B.A software GPS receiver for weak signals[C]//Proceedings of the 2001 IEEE MTT-S International Microwave Symposium Digest.Piscataway: IEEE, 2001: 2139-2142.

[7] Psiaki M L.Block acquisition of weak GPS signals in a software receiver[C]//Proceedings of Ion GPS.Salt Lake City, 2001: 2838-2850.

[8] Zhu C, Fan X.A novel method to extend coherent integration for weak GPS signal acquisition[J].IEEE Communications Letters, 2015, 19(8):1343-1346.

[9] Foucras M, Ekambi B, Bacard F, et al.Optimal GNSS acquisition parameters when considering bit transitions[C]//Position, Location and Navigation Symposium-PLANS 2014, 2014 IEEE/ION.IEEE, 2014:804-817.

[10] Zhu C, Fan X.GNSS signal acquisition in weak signal condition[C]//Networks & Digital Signal Processing of the International Symposium on Communication Systems.IEEE, 2014: 1128-1132.

AvoidingBitTransitionAcquisitionAlgorithmforWeakGPSSignal

CHENGYan,CHANGQing,LIXian-xu

(BeiHangUniversity,Beijing100191,China)

In order to enhance the sensitivity of Global Position System (GPS) receivers, increasing the coherent integration time is necessary for the signal acquisition process.This paper analyzes how the bit sign transition limits the coherent integration time and proposes a novel acquisition algorithm to avoid the bit sign transition limitation.The method employs coherent integration combing with non-coherent integration.By comparing the integration results of the several blocks, the maximum integration result is selected and is used to determine whether to acquire.The algorithm extends the coherent integration time to19ms.The purpose is to make the block of the maximum integration result completely avoid bit transition, and avoid the influence of navigation data bit transition on the results of the coherent integration.The algorithm extends the coherent integration time to the greatest extent on the basis of avoiding bit transition, and then improves the acquisition sensitivity of the GPS receivers.The simulation results show that the acquisition sensitivity has been improved, and the algorithm can acquire the weak signal with Carrier-to-Noise Ratio (CNR) as low as26dB·Hz.

Coherent integration; Bit sign transition; Non-coherent integration; High sensitivity

2017-03-15；

：2017-04-20

：国家自然科学基金(61471021)

：程燕(1987-)，女，博士生，主要从事卫星导航方面的研究。E-mail:chengyan178@163.com

10.19306/j.cnki.2095-8110.2017.05.016

TP391

：A

：2095-8110(2017)05-0094-06