基于Matlab的信号釆样与重构仿真

别业广，凃玲英

基于Matlab的信号釆样与重构仿真

别业广1，凃玲英2

（1湖北工业大学理学院，湖北武汉430068；2湖北工业大学电气与电子工程学院，湖北武汉430068）

在工程实际中，为了对信号进行有效地传输和处理，往往要将连续信号进行采样离散化，以便计算机分析处理。利用Matlab强大的信号处理能力，对一段音乐信号进行采样，在满足采样定理的前提下实现信号的重构。对信号进行截断处理后的采样频谱不发生混叠，重构后的信号误差小，播放的音乐音质保持比较完整。

带限信号；信号的采样；信号的重构；滤波器

现实生活中的速度、温度、压力等大多是连续信号，而计算机处理的则是离散信号。为了对有用信号进行有效传输和处理，需对连续信号进行采样。经采样后，连续信号就变成了离散信号。如何利用这些采样值在不丢失原信号中的信息量的前提下重构原连续信号？以电影为例，电影是由一组按时序的单个画面所组成，每一幅画面代表连续变化景象的一个瞬时画面（时间样本），当以足够快的速度来观看这些时序样本时，就会重现原来连续活动景象。故而，要想确保连续信号采样后能够恢复原信号，必须遵循采样定理。

1 带限信号的采样及重构

1.1 带限信号采样原理

理想采样信号fs（t）是一个连续信号f（t）与一个冲激串δT（t）的乘积，T是抽样周期（图1）。

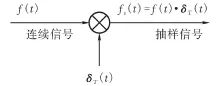
图1 信号采样原理图

若设f（t）是带限信号，其频谱为F（jω），带宽ωm，f（t）经采样后的频谱为FS（jω），则有

图2 当ωs≥ωm理想采样及其频谱

由图2知，带限信号f（t）经采样后的频谱FS（jω）就是将F（jω）在频率轴上搬移至0，±Ω，± 2Ω，...±nΩ处。因此，只有当采样率Ω≥2ωm时，采样后的频谱FS（jω）不发生混叠。采样信号保留了原信号f（t）的全部信息。而当Ω＜2ωm时，频谱发生混叠。

1.2 信号的重构原理

信号f（t）被采样后所形成的采样信号为fs（t），信号的重构是指由fs（t）经内插处理后，恢复信号f（t）的过程，也就是恢复信号的过程。

从抽样信号fs（t）恢复至原信号f（t），即由离散信号变为连续信号。在满足抽样率Ω＝ωS≥2ωm的条件下，只要用一个截止频率为ωm＜ωC＜（ωS－ωm）的理想低通滤波器就可以从FS（jω）中完全取出F（jω）的所有信息。图3是为重构f（t）的原理图。

图3 低通滤波器恢复原信号

2 采样定理在实际工程中的应用

2.1 信号的采样及重构

为了能从抽样信号fS（t）中恢复信号f（t），必须满足两个条件：

1）被采样的信号f（t）必须是有限频带信号，其频谱在｜ω｜＞ωm时为零；

2）采样频率Ω＝ωS≥2ωm带限信号只有满足抽样定理中的抽样频率ωS≥2ωm条件，采样后的频谱FS（jω）才不会产生频谱混叠。这样，采样信号保留了原信号f（t）的全部信息。当不满足抽样定理，即ωS＜2ωm，则频谱将产生混叠，不能恢复原信号。

许多实际工程信号不满足带限条件，这时可以根据实际精度要求来确定信号的带宽ωm，需在采样前将信号通过抗混叠低通滤波器处理，图4用一个截止频率ωm的低通滤波器将F（jω）中振幅较小的高频分量截断，人为形成带限信号F1（jω）。然后分别对这两种信号均用采样率ωS＝2ωm进行采样并对其频谱进行比较，发现没有经过截断处理的信号采样后出现严重的混叠现象，信号无法重构。而经过截断处理的信号虽然有部分高频分量截断，但无混叠，信号重构误差小。

图4 经过截断处理后的误差远小于混叠所产生的误差

2.2 仿真实验分析

为了比较由采样信号恢复后的信号与原信号的误差，用Matlab仿真软件对一段音乐读取，画出这段音乐的频谱图（图5），可知其截止频率约为11000 Hz，由于其带宽太大，在满足精度要求的前提下，对该信号进行进行高频截断处理，将幅度较小的高频分量进行截断，截止频率约为2200Hz，其频谱如图6所示，然后分别对这两种信号进行采样（图5、图6）。根据采样定理，取采样率ωS＝4410Hz，（ωS≥2ωm）。用仿真软件对采样信号进行内插，重构这二个信号，并播放这两段音乐。发现没有经过截断处理的信号由于采样后其频谱发生了混叠，重构后的信号有较大误差，播放音乐时有明显的残余噪声；而对进行了截断处理后的信号进行采样，由于其频谱不发生混叠，重构后的信号重构误差小，播放的音乐音质保持比较完整。

图5 未截断处理的原信号的频谱

图6 截断处理后的信号频谱

3 结论

利用MATLAB仿真软件实现系统建模与动态仿真，在实际工程应用中可使信号分析与处理效率大大提高，从而使信号处理工作变得十分简单，有助于提高工程技术人员分析和解决问题的能力。

［1］ 姚天任，江太辉.数字信号处理［M］.武汉：华中科技大学出版社，2001.

［2］ 楼顺天，李博菡.基于MATLAB的系统分析与设计［M］.西安：电子科技大学出版社，2001.

［3］ 王沫然，陈怀琛.Simulink 4建模及动态仿真［M］.北京：电子工业出版社，2002.

［4］ 马兴义.Matlab 6应用开发指南［M］.北京：机械工业出版社，2002.

Signal Sampling and Reconstruction Simulation Based on Matlab

BIE Yeguang1，TU Lingying2
（1.School of Science，Hubei Univ.of Tech.，Wuhan 430068，China；2 School of Electrical and Electronic Engineering，Hubei Univ.of Tech.，Wuhan 430068，China）

In order to effectively transmit and process the signal during engineering practice，it is often necessary to carry on the sampling and discretization of the continuous signal to facilitate the computer analysis processing.In this paper，we use the powerful signal processing capability of Matlab to sample a piece of music signal，and realize the reconstruction of the signal under the premise of satisfying the sampling theorem.As the signal was truncated，the sampled spectrum did not occur aliasing，the reconstructed signal error is small，and the quality of playing music maintains relatively complete.

band limited signal；signal sampling；signal struction；filter

TP211

A

［责任编校：张 众］

1003－4684（2017）04－0029－02

2017－04－07

教育部高等学校物理类专业教学指导委员会研究课题（01－201601－20）

别业广（1964－），男，湖北仙桃人，湖北工业大学副教授，研究方向为理论物理

凃玲英（1963－），女，湖北武汉人，湖北工业大学教授，研究方向为电子信息及嵌入式技术