一道几何题的变式训练
2017-09-17陈艳霞
陈艳霞
平行线的判定和性质是七年级下学期数学的重要内容,要求学生掌握平行线的性质和判定的基本知识及运用.学生对这一部分的基本知识掌握并不感到困难,感到困难的是需要做辅助线的说理题及利用平行线的性质来判定研究两直线的位置关系或者几个角之间的关系问题.通过几何画板对一道题进行演变,再通过添加辅助线反复练习,可使学生很快掌握这一难点并灵活应用.
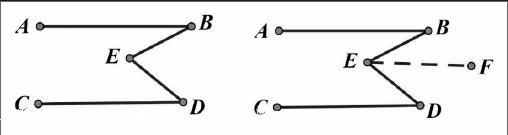
例1:如图,∠BED=70°,∠B=30°,∠D=40,试说明AB∥CD.
通过作辅助线构造内错角,经过分析做法如下:
解:过点E作EF∥AB,
∴∠BEF=∠B=30°,
∵∠BED=70° ,∴∠FED=40°.
又∵∠D=40°,∴∠FED=∠D,
∴EF∥CD, ∴AB∥CD.
变式一:若∠B+∠D=∠BED, AB 、CD有怎样的位置关系?说明理由.
解:AB∥CD.理由如下:
过点E作EF∥AB,
∴∠BEF=∠B,
∴∠BED=∠B+∠FED.
∵∠BED=∠B+∠D,
∴∠D=∠FED,
∴CD∥EF,
∴AB∥CD.
變式二:如图,当AB∥CD时,∠BED、∠B、∠D之间有怎样的关系?说明理由.
解:∠B+∠D=∠BED.理由如下:
过点E作EF∥AB,
∴∠BEF=∠B.
又∵AB∥CD,
∴CD∥EF,
∴∠D=∠FED.
∵∠BED=∠B+∠FED,
∴∠BED=∠B+∠D.
一道题、一个图,辅助线的做法都一样,条件不同,结论就发生变化.由特殊到一般,使学生初步掌握辅助线的做法,对平行线的判定和性质的应用有了更进一步的认识.
利用几何画板把这个图形稍加改动,这道题又会有怎样的变化呢?利用几何画板把点E慢慢拽到如下图所示的位置,让学生清晰地看到图形怎样从左图变化到右图,附加条件和结论,引导学生进行变式训练.
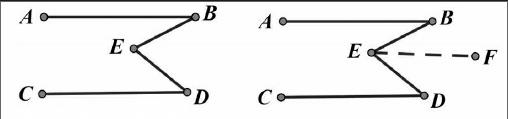
变式三:若AB∥CD,∠BED、∠B、∠D之间有怎样的关系?说明理由.
通过做辅助线构造同旁内角,经过分析做法如下:
解:∠B+∠D+∠BED=360°.理由如下:
过点E作EF∥AB,
∴∠B+∠BEF=180°.
又∵AB∥CD,
∴CD∥EF,
∴∠D+∠FED=180°,
∴∠B+∠BEF+∠D+∠FED=360°.
即∠B+∠D+∠BED=360°.
引导学生思考:把条件和结论交换,结果是否成立?学生讨论,教师参与.
变式四:若∠B+∠D+∠BED=360°时,AB 、CD有怎样的位置关系?说明理由.
解:AB∥CD.理由如下:
过点E作EF∥AB,
∴∠B+∠BEF=180°.
∵∠B+∠D+∠BED=360°,
∴∠D+∠FED=180°,
∴CD∥EF,
∴AB∥CD.
利用几何画板把上述图形中的点E拽到AB、CD的上方,并对最后一种情况给出条件和结论,进行变式训练,学生讨论,得出变式五.
通过做辅助线,构成内错角.
变式五:如图,当AB∥CD时,你能得出∠BED、∠B、∠D之间有怎样的关系吗?说明理由.
解:∠D-∠B=∠BED.
过点E作EF∥AB,
∴∠BEF=∠B.
∵AB∥CD,
∴CD∥EF,
∴∠D=∠FED.
∵∠FED-∠BEF=∠BED,
∴∠D-∠B=∠BED.
把条件和结论进行交换,得出新的变换.
变式六:如图,当∠D-∠B=∠BED时,AB 、CD有怎样的位置关系?说明理由.
解:AB∥CD.理由如下:
过点E作EF∥AB,
∴∠BEF=∠B,
∵∠FED-∠BEF=∠BED.
又∵∠D-∠B=∠BED,
∴∠D=∠FED,
∴CD∥EF,
∴AB∥CD.
还可以把点E拽到AB、CD的下方,让学生尝试自己编题并通过几何画板进行演示.
通过几何画板拽动点E,既直观又形象地完成了图形变化.在平行线的判定与性质这一节中,过一点作已知直线的平行线这一辅助线的做法得到了充分练习,更重要的是,通过图形的变化,使学生学会了这一类型题的做法,以后再遇到同一类题型,学生就会很快识别并迅速作答了.endprint
