基于贝叶斯法的定时截尾小样本指数型装备器材需求预测

王铁宁， 吴龙涛， 杨 帆

(装甲兵工程学院技术保障工程系， 北京 100072)

基于贝叶斯法的定时截尾小样本指数型装备器材需求预测

王铁宁， 吴龙涛， 杨 帆

(装甲兵工程学院技术保障工程系， 北京100072)

针对高新装备器材故障数据少、需求规律不明确的问题，提出了一种定时截尾小样本条件下指数型装备器材的需求预测方法。基于贝叶斯法进行了装备器材寿命分布参数估计，讨论了先验分布和损失函数的选择问题。引入了K-S检验法对寿命分布模型进行拟合优度检验，并设计了寿命分布参数估计的卡方检验方法。综合考虑故障更换和定时更换，提出了部队装备器材年度需求预测方法，并采用蒙特卡洛法进行了仿真验证。结果表明:基于贝叶斯法的参数估计结果能够顺利通过检验，需求预测结果与仿真结果一致。

定时截尾小样本; 装备器材； 指数分布； 需求预测； 贝叶斯法

随着部队高新装备列装步伐的加快和换件修理方式的广泛开展，装备器材需求结构逐渐发生变化，如对光电类及总成类装备器材的需求量显著增加。由于高新装备列装时间短，当前高新装备器材保障普遍存在消耗规律掌握不清、保障不及时的难题。

目前，我军主要采用定额计算[1]方法管理库存，各级仓库一般依据库存标准，并结合现有库存来制定需求计划。但由于库存标准本身就是粗略、不精确的估计[2]，因此定额计算方法难以精确测算装备器材需求。同时，由于高新装备服役时间短，可利用的历史数据较少，故难以应用传统的基于大样本的方法，如时间序列分析、回归分析和神经网络方法等进行器材需求预测。灰色预测模型[3]是小样本预测经常采用的方法，但其预测精度较低，且无法计算装备器材满足率。

基于可靠性的需求预测方法根据失效机理选择装备器材寿命分布类型[4]，并以此建立装备器材需求计算模型。然而，由于装备承制单位在交付装备时往往无法提供其寿命分布的具体形式，且不同部队的装备使用和维护水平以及使用环境差异明显，装备承制单位提供的数据只能作为参考[5]。因此，笔者针对定时截尾小样本，提出了基于贝叶斯法[6]的指数型装备器材的需求预测方法，利用贝叶斯法估计装备器材的寿命分布参数，然后综合考虑故障更换和定时更换，给出了装备器材的需求预测方法，并进行了仿真验证。

1 指数型寿命分布参数估计

1.1指数分布的一般形式

指数分布的重要特性之一是故障率λ(t)=λ为常数，即产品在下一时刻故障失效的概率与已使用时间无关，这也被称作指数分布的“无后效性”[7]。设某装备器材寿命T服从指数分布，其概率密度函数、累积分布函数和产品的可靠度函数分别为

f(t)=λexp(-λt),(t,λ>0)，

(1)

F(t)=1-exp(-λt),

(2)

R(t)=exp(-λt)。

(3)

E(T)=1/λ，为指数分布的期望，即产品的期望寿命(Mean Time To Failure，MTTF)。由指数分布的一般形式可知：对指数型装备器材进行可靠性估计就是估计故障率λ。极大似然估计法是一种在大样本条件下简单有效的参数估计方法，但在截尾小样本情形下偏差较大，且不易收敛[8]。贝叶斯法可充分利用专家经验、装备承制单位的参考数据等先验信息来提高参数估计的准确性，同时随着新信息的出现可不断更新结果，是解决小样本数据预测的有效方法[9]。

1.2故障率λ先验分布的选择

应用贝叶斯法进行寿命分布参数估计时，首先要为参数选择合适的先验分布。通常可选择无信息先验分布和有信息的共轭先验分布。

1)当关于待估参数的先验信息很少时，一般选择无信息先验分布。根据最常用的确定无信息先验分布的Jeffreys法则[9]，λ的先验分布为

π(λ)=λ-1。

(4)

2)共轭先验分布是指与后验分布属于同一类分布的先验分布。伽马分布为指数分布故障率λ常用的共轭先验分布，即λ～Γ(α,β)，其概率密度函数为

(5)

式中：α,β>0，为先验分布的超参数，其值通常根据先验信息使用矩估计法来确定；Γ(α)为伽马函数。

1.3故障率λ的贝叶斯估计

在装备维修过程中，装备器材的更换原因大致分为2类：因故障失效被更换和到了指定的维修间隔期进行等级维修时被更换。因此，可将装备器材的更换时间样本视为定时截尾样本，截尾时间为定时维修间隔期。

设装备的定时维修间隔期为t*，装备器材更换时间样本t的容量为n，故障失效时间数量为z，第i(1≤i≤z)个故障失效时间为ti，则样本的联合分布密度函数为

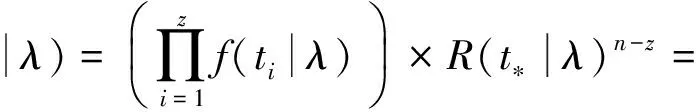
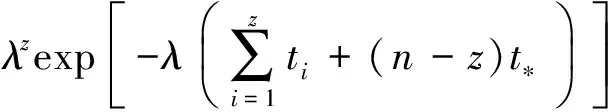
(6)

1)若选择无信息先验，则样本t和λ的联合概率分布为

(7)

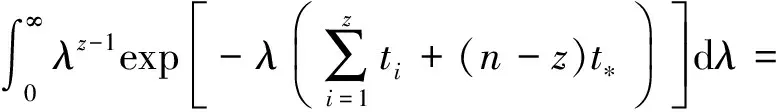
(8)

根据贝叶斯定理，在给定样本t下，λ的后验分布密度函数为

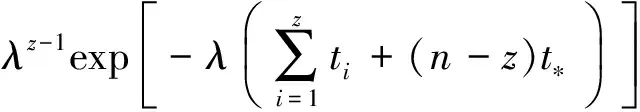
(9)

即

(10)

2)若选择共轭伽马先验，λ的后验分布密度函数为

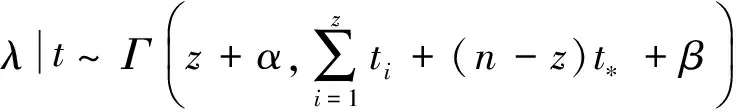
(11)

(12)

(13)

2 寿命分布参数估计检验

2.1寿命分布模型的拟合优度检验

通过贝叶斯估计确定了装备器材寿命分布的形式后，就需要通过寿命分布的拟合优度检验来验证分布模型是否适用于样本。χ2检验是一种常用的拟合优度检验方法，但只适用于大样本(n≥50)完全数据的情形，针对小样本定时截尾数据，笔者引入了K-S检验法[5]。

设装备器材寿命T的真实分布函数为Ψ(t)，则检验假设为

H0:Ψ(t)=F(t)；H1:Ψ(t)≠F(t)。

K-S检验的统计量为

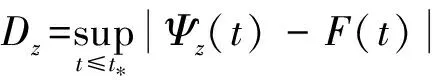
(14)

式中：Ψz(t)为寿命T关于给定失效样本的经验分布函数。由于Ψz(t)是小样本，其计算公式[11]为

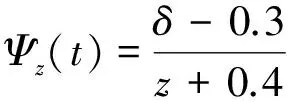
(15)

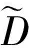
2.2参数估计的假设检验

若默认装备器材寿命T服从指数分布，则只需要对λ的估计结果进行假设检验。且检验假设为

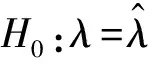
3 指数型装备器材需求预测

图1为部队装备器材需求发生的一般过程。

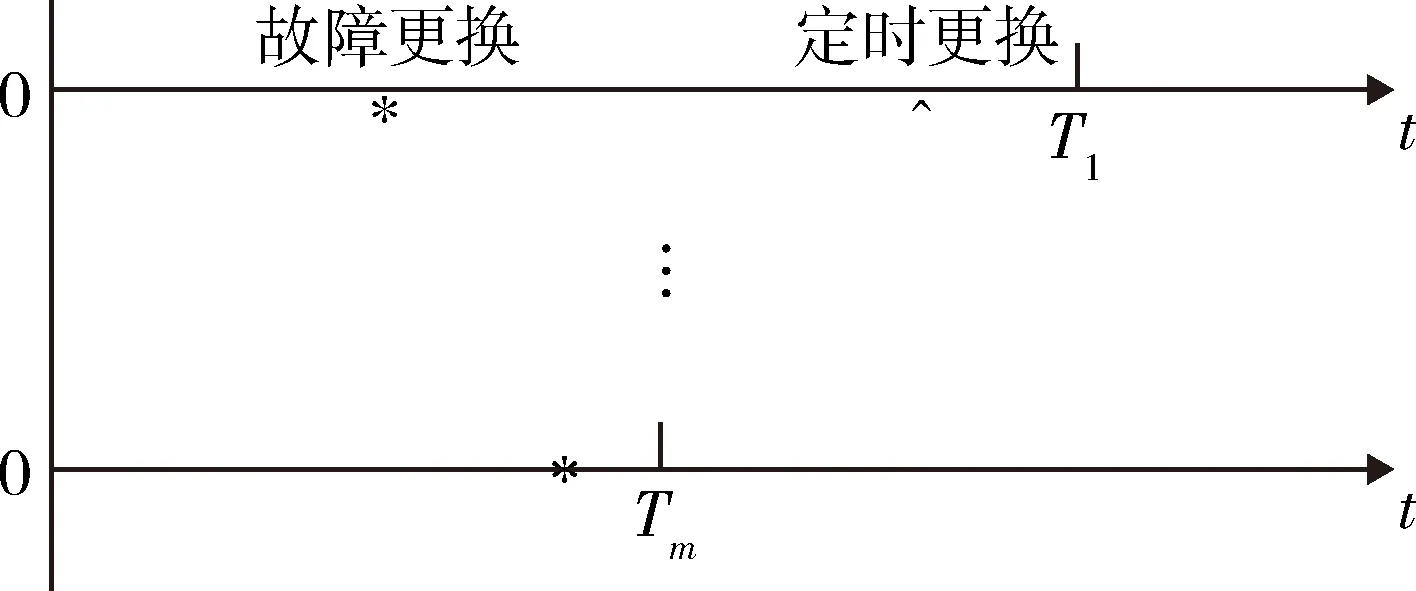
图1 部队装备器材需求发生一般过程

假设某部队有A型现役装备m台，每台装备有1件器材a。根据滚动式循环动用原则，一般每台装备的年度动用时间不同，设Ti(1≤i≤m)为第i台装备的年度动用时间。为了便于分析计算，进行如下假设：

1)装备器材故障失效时采取换件维修，换件时间忽略不计；

2)装备的动用时间即为装备器材的动用时间；

3)各装备中器材a的寿命相互独立且服从同一指数分布。

在计算装备器材年度需求时，需要分别考虑故障更换需求和定时更换需求。已知寿命服从指数分布的器材a在年度动用时间TS内的故障次数N(Ti)服从泊松分布P(λTi)，即

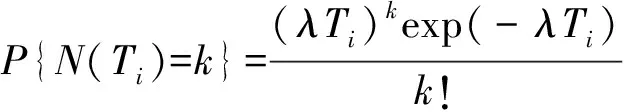
(16)

式中：k∈N。根据泊松分布的可加性可得m件器材a的年度故障次数为N(TS)=N(T1)+N(T2)+…+N(Tm)，服从泊松分布N(TS)～P(λT1+λT2+…+λTm)，即

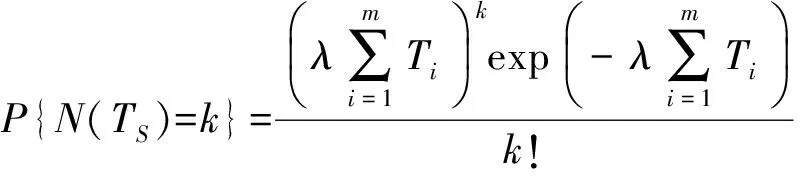
(17)

若规定器材a的年度装备器材满足率为ρ，则因故障更换产生的装备器材需求量S1满足

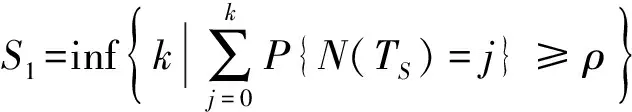
(18)

根据装备维修计划，一般每年都会安排摩托小时已到达定时维修间隔期的装备进行等级维修。在等级维修时，器材a可能采取不更换、必须更换或视情更换3种维修策略[2]，对于视情更换，通常指定一个更换概率p。假设在m台装备中有m0台需要进行等级维修，如器材a不更换，其定时更换需求量S2=0；如必须更换，S2=m0；如视情更换，则S2服从二项分布S2～B(m0,p)，同式(18)，满足率为ρ时的S2为

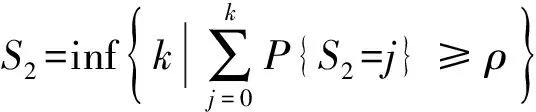
(19)

装备器材a的年度需求量为S=S1+S2。

4 算例分析

以某型装甲车辆的“火控计算机通信板”(简称“通信板”)为例，利用本文提出的方法进行可靠性统计分析和需求预测。已知单台装甲车辆安装一块通信板，通过装备承制单位获知通信板的工作寿命“大约为1 200 h”。某部队在装备动用过程中得到一组更换时间样本为81 h，230 h，274 h，387 h，600 h，688 h，798 h，974 h，1 000*h，1 000*h(带*的为截尾数据)。

4.1参数估计

首先，计算通信板故障率λ的后验分布。若选择无信息Jeffreys先验，由式(10)可得λ的后验分布为Γ(8,6 032)。若选择伽马先验，以装备承制单位提供的数据作为先验信息，设通信板寿命均值为1 200 h，标准差也设为1 200 h，当λ～Γ(α,β)时，MTTF服从IΓ(α,β)分布。应用矩估计法可得

(20)

由式(20)可得先验分布的超参数α=3，β=2 400。再由式(11)可得λ的后验分布为Γ(11,8 432)。图2 为λ先验分布和后验分布的概率密度函数对比分析。可以看出：2种后验分布得到的故障率都高于装备承制单位给出的故障率；同时，由Jeffreys先验得到的后验故障率高于由伽马先验得到的后验故障率，这是因为Jeffreys先验为无信息先验，其后验分布取决于样本。一方面，由于装备承制单位无法预知部队的装备使用环境及装备使用、维修人员的水平，因而高估了通信板的实际使用寿命；另一方面，该样本仅为1次小样本抽样，存在一定的偶然性和不确定性。由伽马先验得到的后验分布综合考虑了装备承制单位先验信息和样本的新信息，因此更加合理。

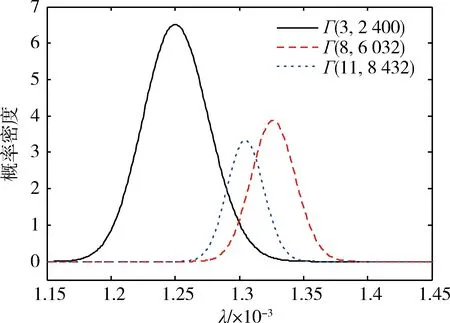
图2 λ先验分布和后验分布概率密度对比

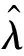
表1 K-S模型拟合优度检验结果

4.2需求预测

假定该单位有该型装甲车辆100台，年度动用计划为(40,15)、(30,25)、(20,60)、(10,150)，并计划安排10台车辆进行等级维修，等级维修时通信板采取视情维修策略，更换概率为0.2，需预测满足率为0.95时通信板的需求量。

为了验证预测结果的准确性，采用蒙特卡洛法对装甲车辆通信板需求预测过程进行仿真。图3为基于MATLAB平台的装备器材需求预测仿真流程。

图3 装备器材需求预测仿真流程

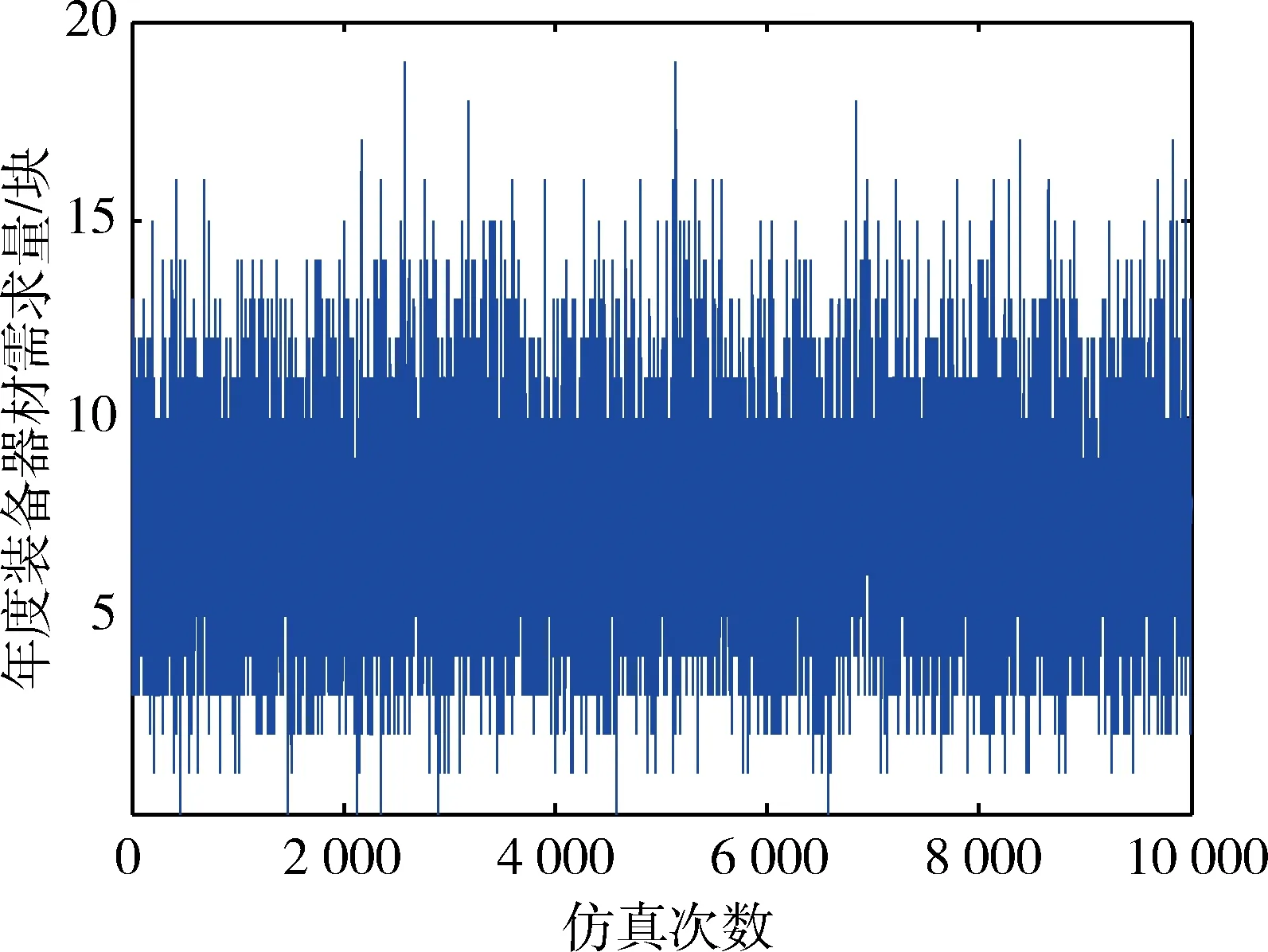
图4 10 000次仿真的年度装甲车辆通信板需求预测样本

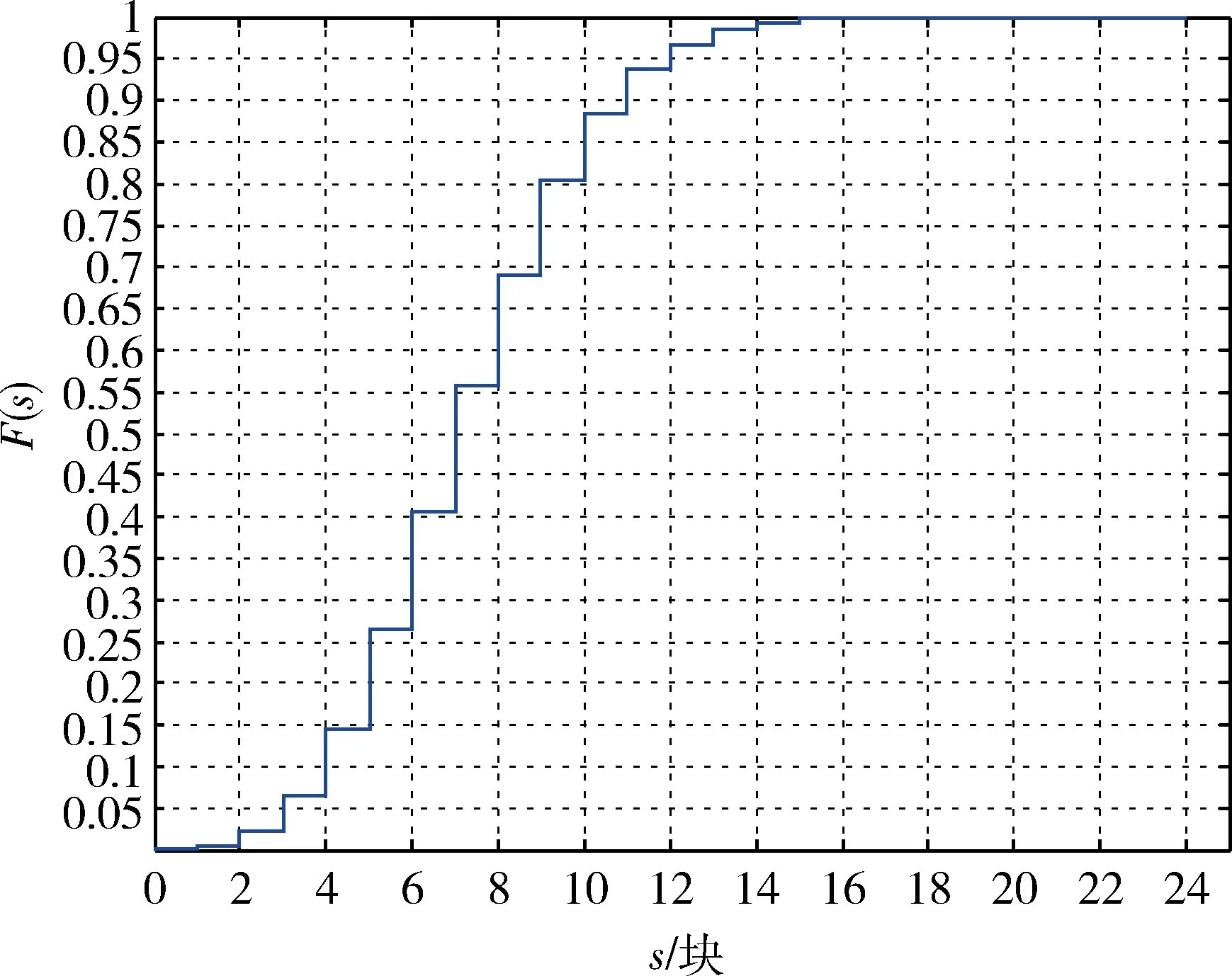
图5 仿真样本的经验分布函数

5 结论

笔者以指数寿命型高新装备器材为对象，结合实际情况，对小样本条件下装备器材的需求预测问题进行了研究。使用贝叶斯法综合了厂家先验信息和使用过程中产生的样本信息，对装备器材的寿命分布参数进行了估计，并给出了分布模型和分布参数的检验方法。在此基础上，综合考虑故障更换和定时更换，提出了装备器材年度需求预测方法，并采用蒙特卡洛法进行了仿真验证，为解决当前高新装备器材消耗规律掌握不清、保障不及时的问题提供了一种可行的方法。

[1] 刘旭阳，吴龙涛，周万里.基于ARIMA模型的装备器材需求预测方法[J].装甲兵工程学院学报，2016，30(6)：21-25.

[2] 刘慎洋，高崎，李志伟，等.基于使用寿命的装备备件消耗预测模型[J].装甲兵工程学院学报，2015，29(4)：27-30.

[3] 郭晓君，刘思峰，吴利丰. 污染物减排预测的灰色Markov组合模型与算法[J]. 计算机应用研究，2013，20(12)：3670-3673.

[4] 李源，杨建军.导弹武器装备备件需求量分析与计算方法[J].兵工自动化，2007，26(8)：22-23.

[5] 蔡景，左洪福，王华伟.基于成本的民用航空发动机维修方案优化研究[J].机械科学与技术研究，2007，26(2)：167-171.

[6] 曾志国.贝叶斯可靠性[M].北京：国防工业出版社，2014：67-70.

[7] 张春晓，周美茵，王志平.基于贝叶斯更新的飞机结构腐蚀可靠度模型[J].航空学报，2014，35(7)：1931-1940.

[8] 冯自立，陈晓阳，顾家铭.Weibull分布下基于矩法的小样本量定时截尾数据的估计[J].四川兵工学报，2010，31(3)：93-97.

[9] SARHAN A.M. Empirical bayes estimates in exponential reliability model [J]. Applied mathematics and computation 2003，135(1)：319-332.

[10] 尹慧琳，杨筱菡，陆恒.Wiener过程性能退化产品可靠性评估新Bayes方法[J].同济大学学报(自然科学版)，2015,43(8)：1234-1237.

[11] EBELING C.E.An introduction to reliability and maintainability engineering [M].New York：Waveland Pr Inc,2009:52-53.

[12] 刘天华，张志华，李庆民，等. 威布尔型多不可修部件备件需求确定方法[J].系统工程理论与实践，2012，32(9)：2010-2015.

(责任编辑: 王生凤)

DemandForecastingforEquipmentMaterialswithExponentialLifeDistributionBasedonBayesianEstimationunderTypeICensoredSmallSample

WANG Tie-ning, WU Long-tao, YANG Fan

(Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing100072, China)

In order to address the problem that the demand discipline of new and high-tech equipment materials cannot be mastered well because of lack of failure data, a method of demand forecasting is proposed for equipment materials with exponential distribution under small failure samples. In a view of small samples, the parameter of equipment material life distribution is estimated by Bayesian estimation, the option of prior distribution and loss function is discussed. Then, statistical tests for goodness-of-fit of the life distribution and parameter estimation are performed by K-S test and Chi-Square test respectively. In consideration of fault replacement and timely replacement, the annual demand forecasting method of army equipment is put forward and devised with a Monte-Carlo simulation test. As the example shows, the estimation result performs well in the test, and the forecasting value is identical to that from the simulation.

type I censored small sample; equipment materials; exponential distribution; demand forecasting; Bayesian estimation

1672-1497(2017)04-0029-06

2017-03-28

军队科研计划项目

王铁宁(1962-)，男，教授，博士。

E92;N945.24

：ADOI：10.3969/j.issn.1672-1497.2017.04.006