部分信息下考虑价格依赖的制造商生产决策研究*

周继祥

(重庆工商大学 商务策划学院，重庆 400067)

部分信息下考虑价格依赖的制造商生产决策研究*

周继祥

(重庆工商大学 商务策划学院，重庆 400067)

针对信息缺失的情形，文章研究了仅知部分市场需求信息下，制造商的生产决策对零售商、制造商的最优决策以及供应链系统绩效和效率的影响。研究发现，需求的期望对供应链绩效的影响远大于方差对供应链绩效的影响。当需求的方差大于零时，供应链的效率会随着需求期望的增加而逼近但不能达到75%；只有方差为零时，供应链的效率才能够达到确定性需求下、线性需求函数的供应链效率。

部分信息；价格依赖；报童模型；供应链效率

订货权是零售商的重要权利。零售商通过调整订货量的多少来影响产品的市场价格，甚至影响上游企业对批发价格的决策和供应链中各个企业以及供应链系统的利润。因此，零售商决策订货量的问题引起了广大学者的广泛关注。一些学者在随机需求的市场环境中研究了零售商订货问题。周艳菊等(2013)运用前景理论，针对随机需求条件下的两产品订货问题进行了研究[1]。王江涛等(2012)研究了零售商主导供应链背景下零售商的订货决策问题[2]。李永飞和苏秦(2013)在随机需求下通过返回策略研究了零售商在分散式、集中式和收益共享情形下的订货问题[3]。张文杰和骆建文(2016)在考虑供应链期权契约的背景下分析了期权契约和传统契约安排下零售商的最优订货决策问题[4]。一些学者考虑了零售商在双渠道或者多渠道背景下的订货决策问题。Huang等(2013)考虑了需求中断情形下零售商的订货决策问题[5]。Hua等(2010)考虑了提前期影响下的零售商双渠道订货定价问题[6]。Dan等(2012)考虑了零售商服务影响下零售商的订货定价问题[7]。禹爱民和刘丽文(2012)等在随机需求下考虑了零售商的订货问题[8]。一些学者研究了资金约束下零售商的订货决策问题。Xu 等(2015)在应收账款融资模式下比较了收益共享契约、成本共享契约和产出惩罚契约对零售商订货的影响[9]。王宗润等(2015)研究了隐性股权下供应链及内容系统中出现资金缺口的供应商通过应收账款融资时零售商的最优策略[10]。Yan等(2016)考虑了一个包含制造商、银行和一个受资金约束的零售商的供应链中，构建了一个双层Stackelberg博弈模型来分析零售商订货决策问题[11]。鲁其辉等(2012)根据供应链应收账款融资交易模型，建立了包含供应商、下游厂商和金融机构的多阶段供应链决策模型，研究了包含和不包含融资情况下相关企业的决策问题，得到供应链中各参与方在各阶段的期望收益[12]。一些学者研究了不同风险偏好下零售商的订货决策问题。Wu等(2009)研究发现当零售商是风险厌恶型决策者时，存库成本对零售商的最优订货决策有着重大的影响[13]。与Wu等(2009)的研究不同，Jammernegg & Kischka(2009)研究了零售商为风险偏好型的决策者的情形[14]。Han等(2014)研究了零售商为风险偏好型以及任意风险厌恶型决策者的情形[15]。还有一些学者从其他角度研究了零售商订货问题。如，冯颖等(2015)针对供应商、第三方物流和零售商组成的生鲜农产品三级供应链，建立了确定性需求情形下零售商的订货决策问题[16]。王宣涛等(2015)在公平中性的供应商、公平关切的零售商和策略型与短视型顾客并存的供应链下研究了零售商的订货和供应链协调问题[17]。王丽颖等(2014)考虑了零售商将未能够在一级市场完全销售出去的产品以折扣价格在二级市场销售的问题，建立了两阶段模型，求解得到了零售商对季节性产品的订货决策[18]。

然而，在竞争激励的市场环境中，零售商和制造商需要改变传统的合作模式，有时零售商不得不让渡部分权利以提高自身利润以及供应链的市场竞争力。另外，在现有研究中，他们要么假设需求是确定性的，要么需求的分布函数为已知。然而，在现实中，由于受到资源或者调查者的预测工具的局限性(Dalrymple,1987)[19]，确切的市场需求信息很难获得，而且有些需求的具体分布形式也可能无法根据历史数据刻画出来。有时候人们只能够得到需求分布的上下界(波动范围)，期望和方差，对称性或者单峰性等信息(Perakis & Roels,2008)[20]。而且在有些新兴行业里面，根本没有历史数据可以查阅；或者在一些产品更新换代非常快的行业，可能还没有来得及对以往的数据进行分析产品就已经换代了；又或者在一些历史数据非常庞大，且可信度未知的行业里，根据历史数据模拟出的产品需求分布信息并不一定可靠。鉴于此，本文在部分需求信息下研究了集中式决策和分散式决策下制造商订货对零售商、制造商以及供应链的利润和效率的影响。

一、模型描述与假设

考虑由一个制造商和一个零售商构成的两级供应链。供应链中，对市场需求具有部分信息的零售商销售单一报童产品。在销售季节开始前，制造商根据其与零售商共同掌握的市场需求信息制订生产任务，假设生产数量为q，单位生产成本为c。销售季节开始时，制造商将观察到市场的具体需求，如果生产的数量不足以满足市场需要，制造商将以单位成本v(v>c)进行第二次生产，并以单位价格w将市场实际需要的产品数量销售给零售商。假设制造商可以将产品立即送到零售商处，即送货提前期为零。零售商收到产品后按照单位价格p进行销售。不失一般性，假设零售商的单位销售成本为零。

根据Mills提出的不确定性定价理论，假设零售商的需求函数为d=y(p)+ε，其中y(p)为销售价格p的减函数，ε是与p无关的随机变量。本文采用Mills对需求函数的假设，假设零售商的需求满足d=a-bp+ε，a>0，b>0。由于本文主要探讨部分信息下制造商生产决策对零售商、制造商和供应链系统决策和利润的影响，因此，本文将零售商需求函数中的参数a,b全部标准化为1。即，零售商的需求函数为d=1-p+ε。令F(ε)和f(ε)分别表示随机变量ε的累积分布函数和概率密度函数。然而，由于零售商能力有限，无法掌握到足够的产品销售数据，或者由于其他方面的原因，零售商无法知晓F(ε)和f(ε)的具体形式，而仅仅知道ε的期望和标准差，假设其期望为μ，标准差为σ。

为使模型简单，易于理解，做如下基本假设：

(1)零售商与制造商都是风险中性的，即，他们都是以利润最大化为决策目标；

(2)制造商作为领导者与零售商进行Stackelberg博弈；

(3)博弈双方具有完全信息。

符号说明

p为零售商的销售价格，决策变量；

w为产品的批发价格，决策变量；

q为制造商第一次生产产品的数量，决策变量；

c为制造商第一次生产产品时的成本；

v为制造商第二次生产产品时的成本；

下标D表示分散式决策的情形，C表示集中式决策的情形。

二、分散决策的情形

(一)零售商的最优决策

由于制造商作为领导者与零售商进行Stackelberg博弈，二者的博弈符合完全信息下动态博弈的条件，我们可以采用逆向归纳法求解。在制造商的初次生产数量和销售价格给定的情况下，零售商以期望利润最大化为目标。当制造商初次生产数量高于实际需求时，零售商将按照实际需求数量采购；当制造商初次生产数量低于实际需求时，制造商将会进行二次生产以补足数量差异。因此，无论制造商初次生产数量为多少，零售商都能够满足实际需求的需要。因此，零售商的利润函数可以表示如下：

πR(p)=(p-w)E(d)

(1)

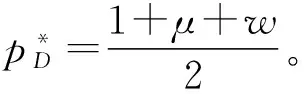
证明：由已知条件，E(d)=1-p+μ，将πR(p)对p分别求一阶、二阶导数可得：

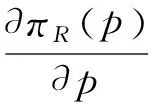
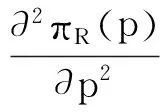
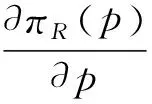
由命题1可知，零售商的最优销售价格与制造商初次生产产品的数量无关，而只与制造商的销售价格以及随机变量的期望有关，且零售商的销售价格将随着制造商的销售价格以及随机变量的增加而增加。

由文章假设可知，无论制造商初次生产产品的数量为多少，零售商最终都能够且只采购与实际需求数量一致的产品。因此，制造商初次生产产品的数量不会对零售商的最优销售价格产生影响。而制造商销售价格的增加将导致零售商采购成本的增加，此时零售商将提高销售价格以减少成本增加对最终利润的冲击。随机变量期望的增加将提高市场需求量，由经济学原理可知，在其他条件不变的情况下，销售价格随着需求量的增加而增加。

(二)制造商的最优决策

由上述分析可知，制造商的利润函数可表示如下：

πM(q,w)=wE(d)-cq-vE[(d-q)+]

(2)

其中，第一项表示制造商将产品卖给零售商获得的收入，第二项表示制造商初次生产产品的成本，第三项表示零售商第二次生产产品的成本。

由于市场需求d=1-p+ε中随机变量ε的分布函数未知，无法运用传统报童问题的求解方法进行求解。考虑到现实中有相当一部分决策者是保守决策者，因此，本文假设制造商是保守决策者。根据Scarf(1958)对部分信息下问题的处理方法的研究[21]，可以将制造商的目标修定为最差分布下的最大利润。从而，制造商的目标函数可以表示为：

(3)

首先求解(3)式的内层函数，即在所有满足期望和标准差为μ和σ的分布函数中找到一个对制造商最不利的F(ε)。为求解(3)式，我们首先引入引理1。

证明：根据Gallego和Moon(1993)[22]的研究可知

E[(d-q)+]

(4)

结合(4)式与(3)式可得引理1。

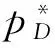
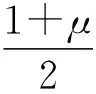
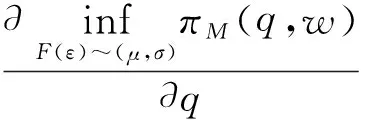
(5)

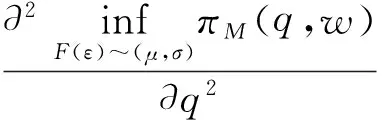
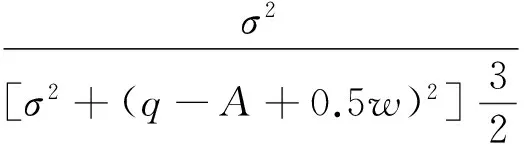
(6)

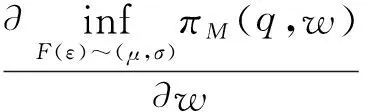
(7)

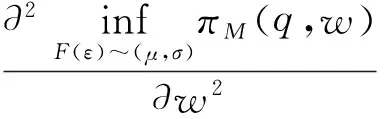
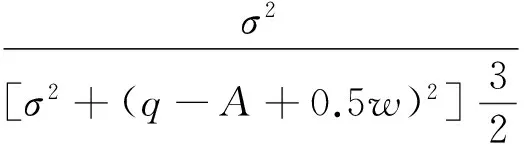
(8)

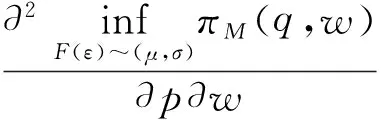
(9)

三、集中决策的情形

集中决策情形下，供应链系统的利润等于零售商和制造商利润之和。则，集中式决策情形下供应链系统的利润可表示如下：

π=pE(d)-cq-vE[(d-q)+]

(10)

集中式决策下，制造商和零售商合为一家，制造商的销售价格不再作为决策变量。此时，供应链的决策变量减少为两个，即产品的最终销售价格和初次生产产品的数量。

命题3：在已知随机变量ε的期望和标准差为μ和σ的情况下，集中式决策下供应链系统的最优销售价格和最优初次生产数量可表示如下：

证明过程可参考引理1和命题2。

四、数值分析

为了进一步考察零售商将订货权让渡给制造商后，零售商、供应商以及供应链系统在集中式决策和分散式决策情形下的绩效和效率，并进一步分析信息缺失对零售商、制造商和供应链系统的影响，本节将通过算例对集中式决策和分散式决策两种情形进行分析。模型中的相关参数赋值如下：μ=0，σ=0.1，c=0.1，v=0.25。

1.需求的期望对最优决策及利润的影响

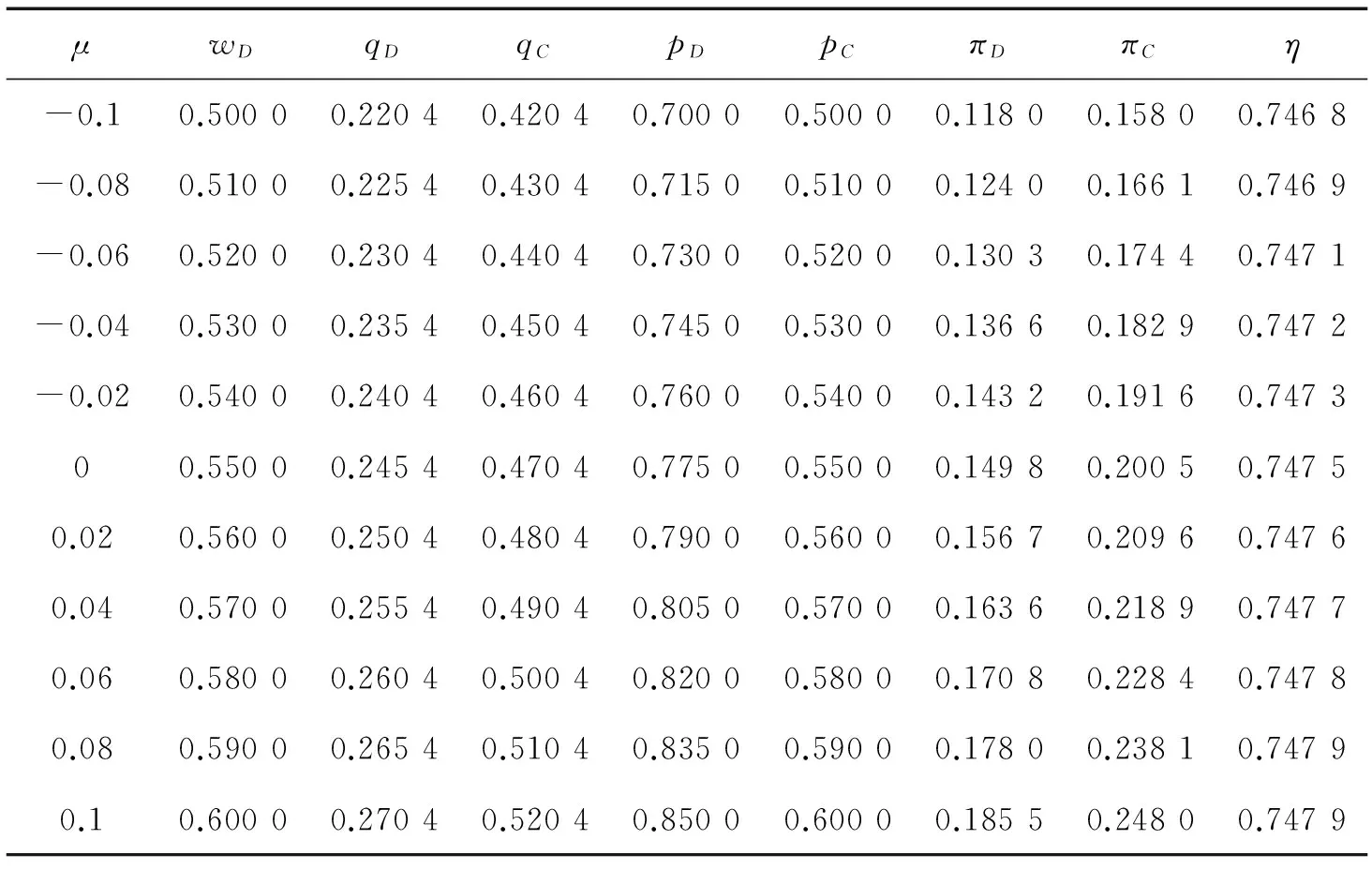
表1 需求期望变化的影响

观察表1可以发现，μ的增加将会引起分散式决策下制造商的最优批发价格的提高，从而直接导致零售商进货成本的增加。零售商为了消除进货成本增加导致的利润下滑，将会提高产品的销售价格。分析需求函数d=1-p+ε可以发现，市场需求不仅收到产品销售价格的影响，还受到随机变量ε的期望μ的影响。观察表1可以发现，μ每增加2单位，产品价格pD将会随之增加1.5单位，增幅较小。因此，市场需求将会随着μ的增加而增加，此时制造商将会提高初次生产产品的数量。即，qD随着μ的增加而增加。同时，由于市场需求、产品销售价格以及批发价格的增加，制造商和零售商的利润将会随之增加，从而会提高供应链系统的绩效。集中式决策情形下，各变量的变化情况同分散式决策相一致。

2.需求的方差对最优决策及利润的影响

在其他条件不变的情况下，当μ=0时，wD,pD,pC与需求的方差变化无关。此时，wD=0.550 0，pD=0.775 0，pC=0.550 0。其他变量变化情况见表2。

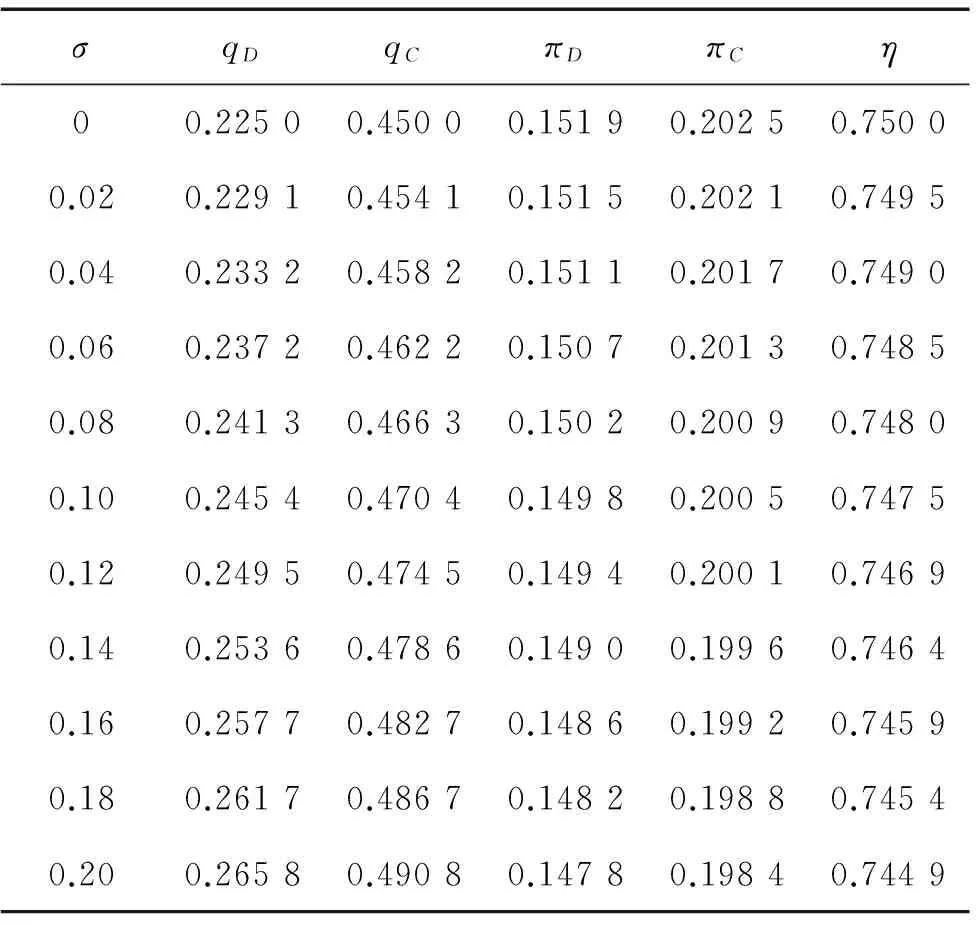
表2 需求方差变化的影响

观察表2可以发现，无论是集中决策，还是分散决策情形下，制造商的初次最优生产量均随着σ的增加而增加，而供应链系统的绩效正好与之相反。σ的增加意味着需求波动幅度的加大，此时为了能够更好地满足零售商的需求，从而避免二次生产时的高成本，制造商将会增加初次生产的数量。σ的增加意味着市场需求的具体数量更加难以确定，供应链中的企业面临的风险更大，因此将会导致供应链系统整体利润的下滑。另外，需求波动幅度的增加还会导致供应链效率的减少。当市场需求波动幅度为零，即σ=0时，供应链的效率达到线性需求函数下供应链效率的最大值75%，这一结论也得到了孙彩虹等(2015)[23]研究的印证。

综合分析表1和表2可以发现，在μ和σ变化幅度相同的情形下，μ对供应链系统利润的影响更大，而σ对供应链效率的影响更大。

五、结束语

研究发现，需求的期望对供应链绩效的影响远大于方差对供应链绩效的影响。当需求的方差大于零时，供应链的效率会随着需求期望的增加而逼近但不能达到75%；只有方差为零时，供应链的效率才能够达到确定性需求下、线性需求函数的供应链效率。本文也存在着一些不足之处，我们没有考虑制造商、零售商在生产和订货过程中的资金问题，在资金约束下，二者的最优决策将会做出怎样的改变？同时，现实中，制造商的生产量也可能是随机的，这些都将是我们的研究内容。

[1] 周艳菊,应仁仁,陈晓红,王宗润. 基于前景理论的两产品报童的订货模型[J]. 管理科学学报,2013,16(11):17-29.

[2] 王江涛,叶飞,徐学军,余建军.随机需求下零售商主导供应链的订单决策分析[J].工业工程与管理,2012,17(2):51-56,89.

[3] 李永飞,苏秦.考虑随机需求及返回策略的供应链协调分析[J].软科学,2012,27(2):50-54.

[4] 张文杰,骆建文.随机产出随机需求下的供应链期权契约模型[J].管理工程学报,2016,30(3):121-128.

[5] Huang S, Yang C, Zhang X. Pricing and production decisions in dual-channel supply chain with demand disruptions[J].Computers & Industrial Engineering, 2013,62:70-83.

[6] Hua G, Wang S, Cheng T.C.E. Price and lead time decisions in dual-channel supply chains[J]. European Journal of Operational Research,2010,205:113-126.

[7] Dan B, Xu G, Liu C. Pricing policies in a dual-channel supply chain with retail services[J]. International Journal of Production Economics,2012,139:312-320.

[8] 禹爱民,刘丽文.随机需求和联合促销下双渠道供应链的竞争与协调[J].管理工程学报,2012,26(1):151-155.

[9] Xu X, Cheng X, Sun Y. Coordination contracts for outsourcing supply chain with financial constraint[J]. International Journal of Production Economics,2015,162:134-142.

[10] 王宗润,田续燃,陈晓红.考虑隐性股权的应收账款融资模式下供应链金融博弈分析[J].中国管理科学,2015,23(9):1-8.

[11] Yan N, Sun B, Zhang H et.al. A partial credit guarantee contract in a capital-constrained supply chain: Financing equilibrium and coordinating strategy[J]. International Journal of Production Economics,2016,173:122-133.

[12] 鲁其辉, 曾利飞, 周伟华. 供应链应收账款融资的决策分析与价值研究[J]. 管理科学学报, 2012, 15(5):10-18.

[13] Wu D, Baron O, Berman O. Bargaining in competing supply chains with uncertainty[J]. European Journal of Operational Research, 2009,197(2):548-556.

[14] Jammernegg W, KischkaA P. Risk preferences and robust inventory decisions[J]. International Journal of Production Economics,2009,18(1):269-274.

[15] Han Q, Du D, Zuluaga LF. A Risk and Ambiguity-Averse Extension of the Max-Min Newsvendor Order Formula[J]. Operations Research,2014,62(3):535-542.

[16] 冯颖,余云龙,张炎治,吴茜.TPL服务商参与决策的生鲜农产品三级供应链协调机制[J].管理工程学报,2015,29(4):213-221.

[17] 王宣涛,张玉林.考虑顾客行为与零售商公平关切的易逝品定价与供应链协调研究[J].管理工程学报,2015,29(1):89-97.

[18] 王丽颖,巩天啸,陈丽华,蓝颖杰.二级市场季节性商品的订购和销售决策[J].管理科学学报,2014,17(5):35- 42.

[19] Dalrymple D J. Sales forecasting practices: Results from a United States survey[J]. International Journal of Forecasting, 1987, 3: 379-391.

[20] Perakis G, Roels G. Regret in the newsvendor model with partial information[J]. Operations Research, 2008, 56(1): 188-203.

[21] Scarf H. A min-max solution of an inventory problem[J]. In: Arrow K, Karlin S, Scarf H (Eds.), Studies in The Mathematical Theory of Inventory and Production. California: Stanford University Press, 1958, 201-209.

[22] Gallego G, Moon I. The distribution free newsboy problem: review and extensions[J]. Journal of the Operational Research Society, 1993: 825-834.

[23] 孙彩虹,田真真,于辉.价格需求函数的供应链合作动力对比分析[J].工业工程, 2015,18(4):58-65.

(责任编校：朱德东)

ResearchonProductionDecisionforPrice-dependentManufacturerwithPartialInformation

ZHOU Ji-xiang

(SchoolofBusinessPlanning,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)

In view of the lack of information, this paper studies the effect of production decision of the manufacturer on the retailer and the manufacturer’s optimal decisions, and the performance and efficiency of the supply chain system. This study finds that the influence of demand expectation on supply chain performance is bigger than that of the variance. When the variance of demand is bigger than zero, the efficiency of the supply chain will increase and be close to but less than 75%. And only the variance is equal to zero, the value of the supply chain efficiency can reach the supply chain efficiency under the condition of deterministic demand and linear demand function.

partial information; price-dependent; newsvendor model; supply chain efficiency

10.3969/j.issn.1672- 0598.2017.05.004

2017- 01-12

国家自然科学基金项目(71672015)；重庆市社会科学规划博士培育项目(2015BS032)；山东省高等学校人文社会科学研究项目(J15WB54)；重庆市教委科技项目(KJ1600609)；重庆工商大学高层次人才科研启动项目(950316037)；重庆工商大学校内项目(670101561)

周继祥(1986—)，男，江苏徐州人：博士，重庆工商大学商务策划学院讲师，主要从事供应链管理，供应链金融研究。

F253.4

：A

：1672- 0598(2017)05- 0026- 06