衍射光栅铝膜纳米压痕基底效应有限元模拟研究

张宝庆，王占鹏，张安坤，郑志涛

（长春理工大学 机电工程学院，长春 130022）

衍射光栅铝膜纳米压痕基底效应有限元模拟研究

张宝庆，王占鹏，张安坤，郑志涛

（长春理工大学 机电工程学院，长春 130022）

为探究衍射光栅铝膜基底效应对纳米压痕过程的影响，基于ABAQUS有限元分析软件，采用对比分析的方法，建立有基底铝膜和无基底铝膜模型，模拟纳米压痕的压入过程。结果表明，当出现基底效应后，有基底铝膜的回弹量比无基底铝膜小，隆起高度先比无基底铝膜小，之后大，载荷比无基底铝膜大，且基底效应逐渐变大。通过分析铝膜中基底效应对纳米压痕过程的影响，为衍射光栅铝膜力学性能研究提供了重要参考。

衍射光栅铝膜；基底效应；有限元分析

0 引言

衍射光栅是一种非常精密的光学元件具有理想的色散分光功能，广泛应用于各种现代光谱学仪器中[1,2]。衍射光栅的材料由玻璃基底、中间镀铬层和蒸镀铝膜三部分组成。中间镀铬层厚度约为0.1μm，蒸镀铝膜厚度为10μm左右。衍射光栅采用机械刻划工艺在蒸镀铝膜上制作而成。衍射光栅铝膜的力学性能影响衍射光栅的质量。

利用纳米压痕技术获得膜/基体系中纯膜的力学性能时，需要遵循十分之一经验法则，即压入深度小于薄膜厚度的十分之一。

在实际测量薄膜性能的过程中，由于仪器本身的灵敏度、针尖表面状态以及薄膜厚度等各种因素的影响，很难获得有意义的结果。为了探究在不限制压入深度的条件下，如何获得膜/基体系中膜本身的力学性能，D.L.Joslin，W.C.Olive,R.Saha，T.Y.Tsui，A.M.Korsunsky[3～6]等人做了大量的研究。

1 基底效应分析

纳米压痕是最简单的测试材料力学性能的方法之一，其使用压头加载到材料表面，通过得到的测出压痕区域的变化，进而得到材料材料力学性能。有限元分析法是重要的科学研究工具，能够分析压头压入的过程中，材料的应力应变情况，更好地计算分析材料力学行为的变化，为更深入的研究材料力学性能提供了强有力补充。

由于薄膜厚度很薄，在测试薄膜力学力学参数时，应力、应变的分布与传递会受到薄膜、膜基界面和基底材料三者间产生交互作用的影响[7]。当压头下方材料的弹塑性变形区域均在发生在薄膜中的时候，纳米压痕测量结果只是膜的材料力学性能，如图1(a)所示；当压头下方材料的弹塑性变形区进入基底的时候，测量结果是膜和基底耦合的材料力学性能[8]，如图1(b)所示。

2 力学性能计算理论

在纳米压入分析中，硬度的计算由最大载荷和压痕接触投影面积决定。对于形状固定的压头，压痕接触投影面积由等效接触深度确定。最常用的接触深度的计算方法由Oliver和Pharr等[9]提出：

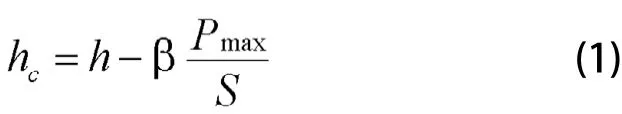
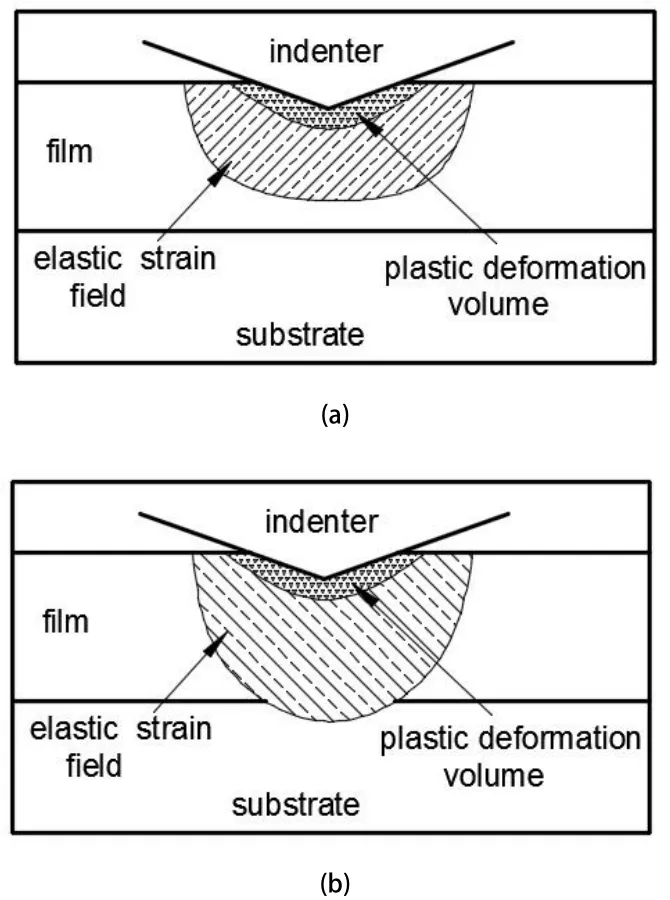
图1 薄膜/基底体系中压头下方弹性和塑性变形场示意图

上式中h为最大压入深度，P和S为相应深度下的载荷和接触刚度，为与压头几何形状有关的参数，对于锥形压头，=0.75。

Oliver-Pharr方法根据载荷-压深关系曲线卸载的前25%-50%的部分拟合，计算得到的材料刚度为：

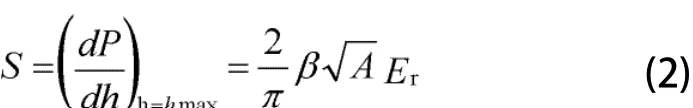
式中：P为压深为h时的载荷，h为压痕深度；

A为压痕接触投影面积；

Er为复合响应模量。

对新车应认真检查保养：部分机手忽略对新拖拉机的检查保养，结果问题频出，追悔莫及。检查保养的方法是：检查三级空气滤清器中油盘内是否有机油；检查各部螺栓的紧固情况；对喷油压力进行检查调整；要换油底壳内机油，清洗油底壳及润滑油路。

由于压头不可能是完全刚性的，因而引入复合响应模量，Er为：

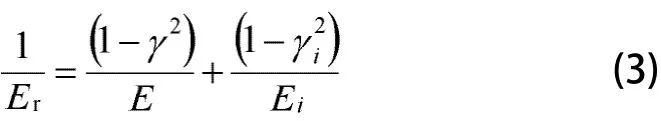
式中E、Ei为分别为被测材料的弹性模量、压头材料的弹性模量；

Oliver和Pharr方法计算得到的硬度公式为：

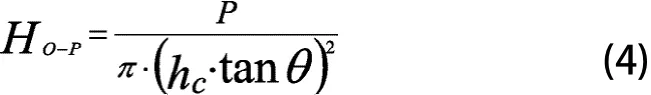
Oliver和Pharr计算方法没有体现材料堆积或收缩的行为特征，对于有这类特征的材料，硬度的计算公式为：

3 模型的建立

实际使用的压头一般都不是标准的圆锥压头，而是三棱锥或者四棱锥。为了简化模型的复杂程度和求解计算量，在有限元模拟中，一般将非标准的圆锥压头简化为锥角为70.3°的圆锥压头[10，11]。压头由金刚石材料制作而成，其弹性模量为1140GPa，泊松比为0.07，在模型中将其视为刚体。薄膜、基底和压头具有轴对称性，为了减少网格数量，简化计算，将其转化为二维模型，衍射光栅铝膜和无基底铝膜的压入模型如图3.1（a）和（b）所示。衍射光栅铝膜的厚度为10μm，Cr层的厚度为0.1μm，模拟中玻璃的厚度为50μm。无基底铝膜的厚度为100μm，使应力场完全在铝膜中。

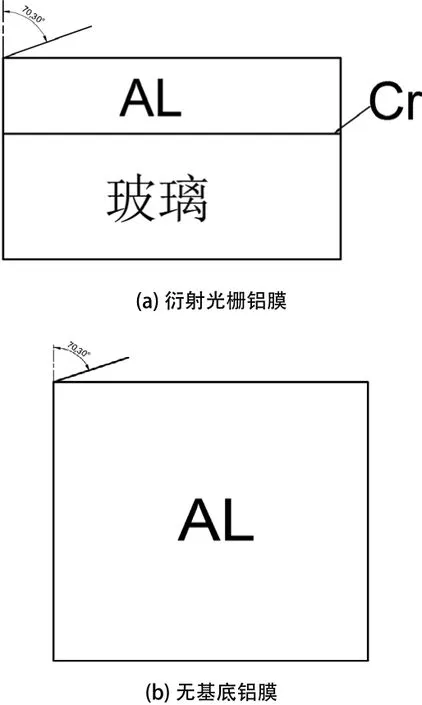
图2 两种模型示意图

模型边界条件为对称中心轴上所有节点只能沿方向发生位移即UX=0，被压试件底面所有节点只能沿方向发生位移即UY=0。载荷是通过轴对称模型的参考点来施加的。网格采用CAX4R单元，在压头附近采用密网格，远离压头逐渐使用稀疏网格，这主要是因为压头附近材料的变形比较大，离压头越远，其变形也越小。材料应力－应变关系遵循幂强化模型，假设材料为均匀且各向同性，遵循Von Mises屈服准则。假设膜基体系中各界面间为理想粘接，压痕过程准静态的，压头与铝膜之间的摩擦设为0.1。

在模拟的过程中，衍射光栅铝膜和基底的参数，如表1所示。

4 有限元模拟与分析

4.1 Cr压痕的实验与模拟

为了检验有限元程序的可靠性，本文使用瑞士CSM公司的NanohardnessTester型纳米压痕仪和金刚石Berkovich压头对Cr样本（50×50×30mm）做压入20μm实验。Cr样本实验结果和有限元模拟结果的载荷-压入深度曲线，如图4.1所示，可以看出两者吻合得较理想，说明有限元程序具有足够的计算精度[12]。

表1 材料参数表

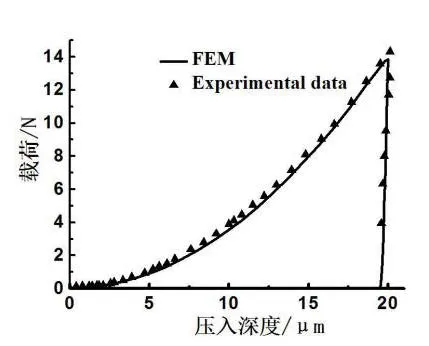
图3 1Cr的压痕实验与模拟结果比较

4.2 压入过程分析

压头逐渐压入，衍射光栅铝膜和无基底铝膜应力示意图，如图4.2所示。

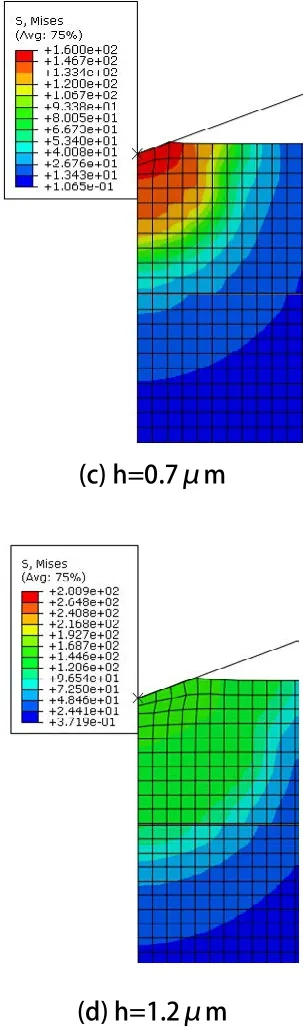
图4 衍射光栅铝膜压入不同深度下的应力场分布

当压入深度小于0.5μm，压头下方的最大应力达到铝膜应变硬化指数对应的屈服强度后，铝膜发生塑性变形，铝膜内的最大应力不在增加，压头下方的应力都在铝膜内。当压入深度为0.5μm时，压头下方应力传递到基底中，使基底发生弹性变形，基底将对铝膜产生反作用力，影响压入过程。随着压入深度的增加，基底内的应力逐渐增大，基底发生弹塑性变形，压头下方的最大应力将在基底内，并达到基底的屈服强度，基底对铝膜压入过程的影响越来越大。随着压入深度的增加，铝膜表面出现隆起的现象，隆起高度逐渐增大。且随着深度的增加，隆起高度逐渐的变大。

此时，获取铝膜纯的力学性能压入最大深度要小于0.5μm，压入深度的十分之一经验法则将不能准确适用。因此利用有限元方法模拟衍射光栅铝膜的纳米压入过程，能够有效地获取压入深度的临界值，为利用纳米压痕法实验获取衍射光栅铝膜纯的力学性能的压入深度提供理论支持。

4.3 压入过程的对比分析

为了分析基底对压入过程的影响，使用有限元软件模拟纳米压入过程，起始压入深度为1μm，每次压入深度增加0.1μm，压入最大深度为4μm。衍射光栅铝膜和无基底铝膜的回弹量、隆起高度、载荷拟合曲线对比，如图4.3.1、4.3.2、4.3.3所示。

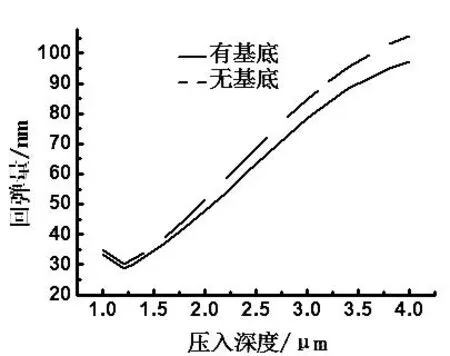
图5 有无基底的回弹量对比图

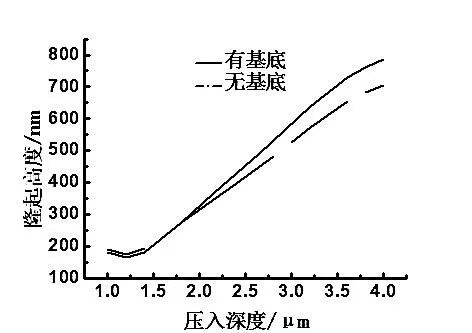
图6 有无基底的隆起高度对比图

图7 有无基底的载荷对比图

随着压入深度的增加，有基底和无基底铝膜的回弹量和隆起高度整体都逐渐的增加，但在1.2μm处出现极小值点。两者表现出相同的变化趋势，即变化量逐渐增大，变化率逐渐变小。有基底和无基底铝膜的载荷逐渐增大且变化率变大。

随着压入深度的增加，基底效应逐渐明显，即有基底铝膜的回弹量要比无基底铝膜小，且两者的差值逐渐增大；有基底铝膜的隆起高度先比无基底铝膜小，之后比铝膜大，且差值逐渐增大；有基底铝膜的载荷要比无基底铝膜的载荷大，两者的差值逐渐增大。

基底效应的存在，使压头与衍射光栅铝膜的接触深度和载荷发生变化，这会影响铝膜力学性能的测量结果，压入深度越大，影响程度越大。

5 结果及讨论

1）有基底铝膜和无基底铝膜的回弹量、隆起高度和载荷，对应的变化趋势相同。在压入深度为0.5μm后，基底效应开始出现，并逐渐明显。

2）基底效应的存在使回弹量变小，隆起高度和载荷变大，这影响衍射光栅铝膜力学性能的测量结果。在光栅刻划精密控形技术中，基底效应的影响，不容怱略。

[1] 王力锋.衍射光栅技术进展[J].光机电信息,1998,15(1):23-25.

[2] 李英海,巴音贺希格,齐向东.用于衍射光栅刻划的超精密金刚石刻刀的研制[J].微细加工技术,2006,(6):15-17.

[3] D. L. Joslin,W. C. Oliver. A new method for a-nalyzing data from continuous depth sensing micro-indentation tests[J].Journal of Materials Research,1990,5:123-126.

[4] R. Saha, W. D.Nix. Effects of the substrate on the determination of thin film mechanical properties by nanoindentation[J].Acta Materialia,2002,50:23-38.

[5] T. Y. Tsui, G. M. Pharr. Substrate effects on nanoindentation mechanical property measurement of soft films on hard substrates[J]. Journal of Materials Research.1999,14:292-301.

[6] A. M. Korsunsky, M. R. McGurk, S.J.Bull，T. F. Page.On the hardness of coated systems[J].Surface and Coatings Technology,1998,99:171-183.

[7] 王勇军.薄膜_基体温度影响下力学性能研究[D].西北工业大学,2007.

[8] 张天林.纳米压入技术中基底和针尖效应的研究[D].中国科学技术大学,2008,5.

[9] W. C. Oliver , G. M. Pharr . An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J].Journal of Materials Research,1992,7(6):1564-1583.

[10] J.G.Swadener,E.P.George,G.M.Pharr.The co-rrelation of the indentation size effect measured with indenters of various shapes[J].Journal of the Mecha-nics and Physics of Solids,2002,50:681-694.

[11] 张帆,黄克智,黄永刚,秦江.摩擦因素对微压痕实验的影响[J].工程力学,2006,23(Z1):1-6.

[12] 马德军,徐可为,何家文.测定金属薄膜屈服强度的纳米压入法研究[J].金属学报,1998,34(6):661-666.

Finite element simulation study of nano-indentation substrate e ff ect of di ff ractive grating aluminum fi lm

ZHANG Bao-qing, WANG Zhan-peng, ZHANG An-kun, ZHENG Zhi-tao

TH164

：A

：1009-0134(2017)08-0084-04

2017-05-16

国家自然科学基金青年基金项目（51405031）；国家自然科学基金面上项目（51575057）；吉林省自然科学基金项目（20150101023JC）；吉林省教育厅“十三五”科学技术研究项目（KYC-JC-XM-2016-030）

张宝庆（1975 -），男，吉林延边人，副教授，博士，研究方向为精密和超精密加工、检测及装备设计。