基于串级模糊自适应PID的起重机防摇控制研究

2017-09-15谌海云

制造业自动化 2017年8期

关键词：拉格朗内环起重机

刘斌，谌海云

（西南石油大学电气信息学院，成都 610500）

基于串级模糊自适应PID的起重机防摇控制研究

刘斌1，谌海云1

（西南石油大学电气信息学院，成都 610500）

以桥式起重机的吊重系统为研究对象，利用拉格朗日方程建立吊重系统的状态空间模型，在Matlab/Simulink中建立控制小车位移和吊重摆角的串级PID防摇控制仿真模型，在内环引入模糊自适应PID控制对串级PID控制模型进行改进。仿真结果显示引入模糊自适应PID控制后，防摇控制系统的控制效果更好，尤其对摆角的控制，超调减小，调节时间加快。最后，利用贝加莱的防摇控制系统实验平台对模糊自适应PID防摇控制系统进行验证。

桥式起重机；Matlab/Simulink；串级PID；模糊自适应PID；贝加莱

0 引言

桥式起重机是港口运输、装备制造等行业重要的装载工具，但在运行过程中小车的加、减速以及风力等外界干扰的影响都会导致吊重货物的摆动。文献[1]综述了防摇控制系统的发展，并介绍人工防摇、机械防摇和电子防摇三种常用的防摇方法。文献[2]中对桥式起重机吊摆系统和变频调速系统进行数学建模，并通过Matlab仿真验证模型的精确性。文献[3]建立以位移和位移变化率为输入的位移模糊控制器，以摆角和摆角变化率为输入的摆角模糊控制器，通过仿真验证双模糊控制器对系统的防摇效果。文献[4]对集装箱起重机的吊摆设备进行仿真分析，并设计基于富士PLC的防摇控制系统用于实际吊装现场中，运行效果良好。

本文基于拉格朗日方程建立起桥式起重机的状态空间模型，在Matlab/Simulink中搭建控制位移和摆角的串级PID控制模型，然后，在串级PID控制的基础上将模糊自适应PID控制引入内环代替原来单纯的PID控制，通过仿真实验对比两种控制方式的控制效果。最后，在贝加莱防摇控制系统平台上对串级模糊自适应PID控制系统进行实验测试，以验证理论分析的结果。

1 起重机防摇系统的数学模型

实际的桥式起重机模型很复杂，为了理论分析的方便，此处对系统模型作简化处理，假设如下：

1）钢丝绳（吊绳）的质量和长度变化忽略不计；

2）风力、空气阻力以及钢丝绳与小车连接处的摩擦力忽略不计；

3）系统的弹性形变忽略不计；

4）将吊起的货物视为无体积的质点。

得到起重机的简化模型如图1所示。

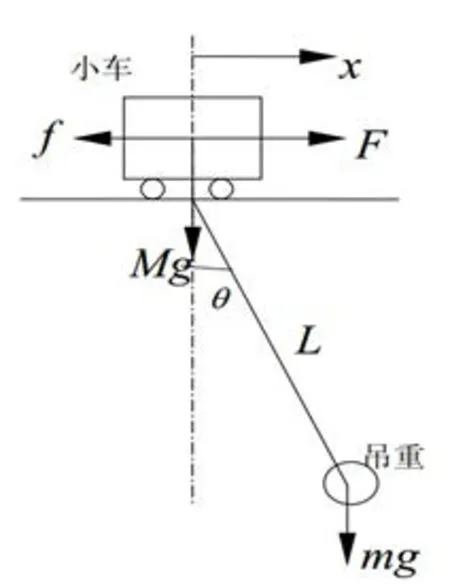
图1 小车、吊重力学简化模型

设小车质量为M（质量单位为kg），吊重质量为m，小车与轨道间的摩擦系数为，钢丝绳长度为L，小车水平驱动力为F，吊重摆角（钢丝绳与垂直方向的夹角）为

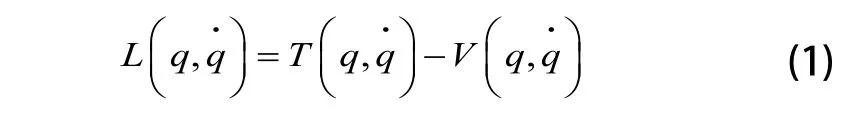
拉格朗日（Lagrange）方程为：

其中，L为拉格朗日算子，T为系统的动能函数，V为系统的势能函数，q,为拉格朗日变量，分别为广义坐标和广义速度。由图2.1可知，以小车质心为坐标原点，设小车和吊重的坐标分别为：

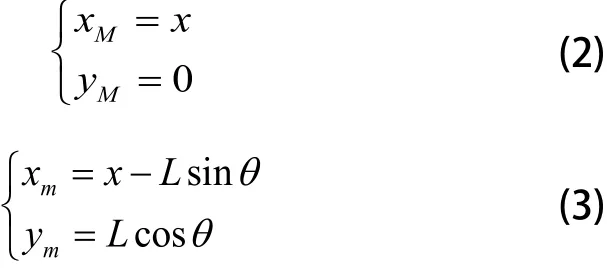
计算得到系统的动能为：

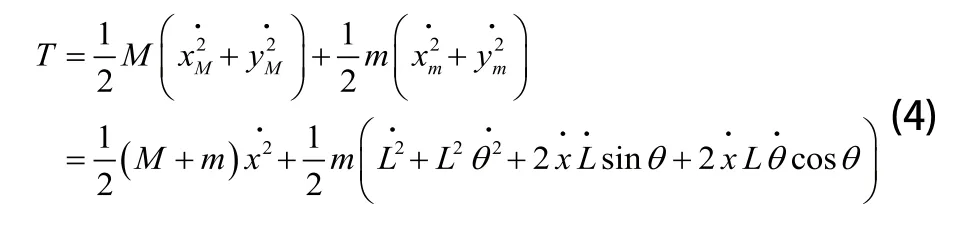
势能为：

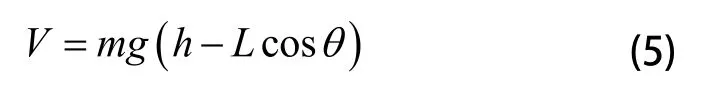
则系统的拉格朗日算子为：

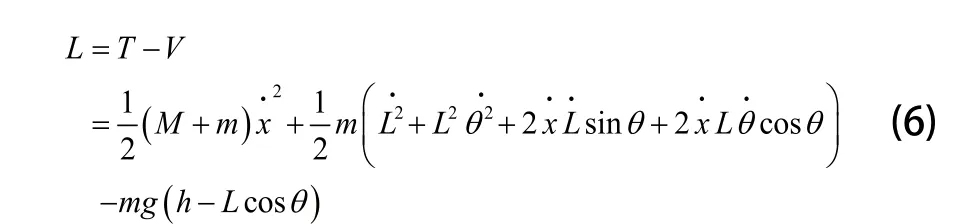
再根据拉格朗日方程建立起桥式起重机的动力学微分方程：

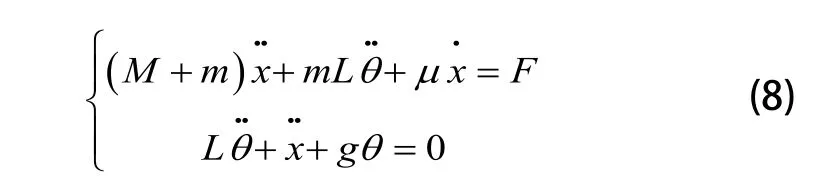
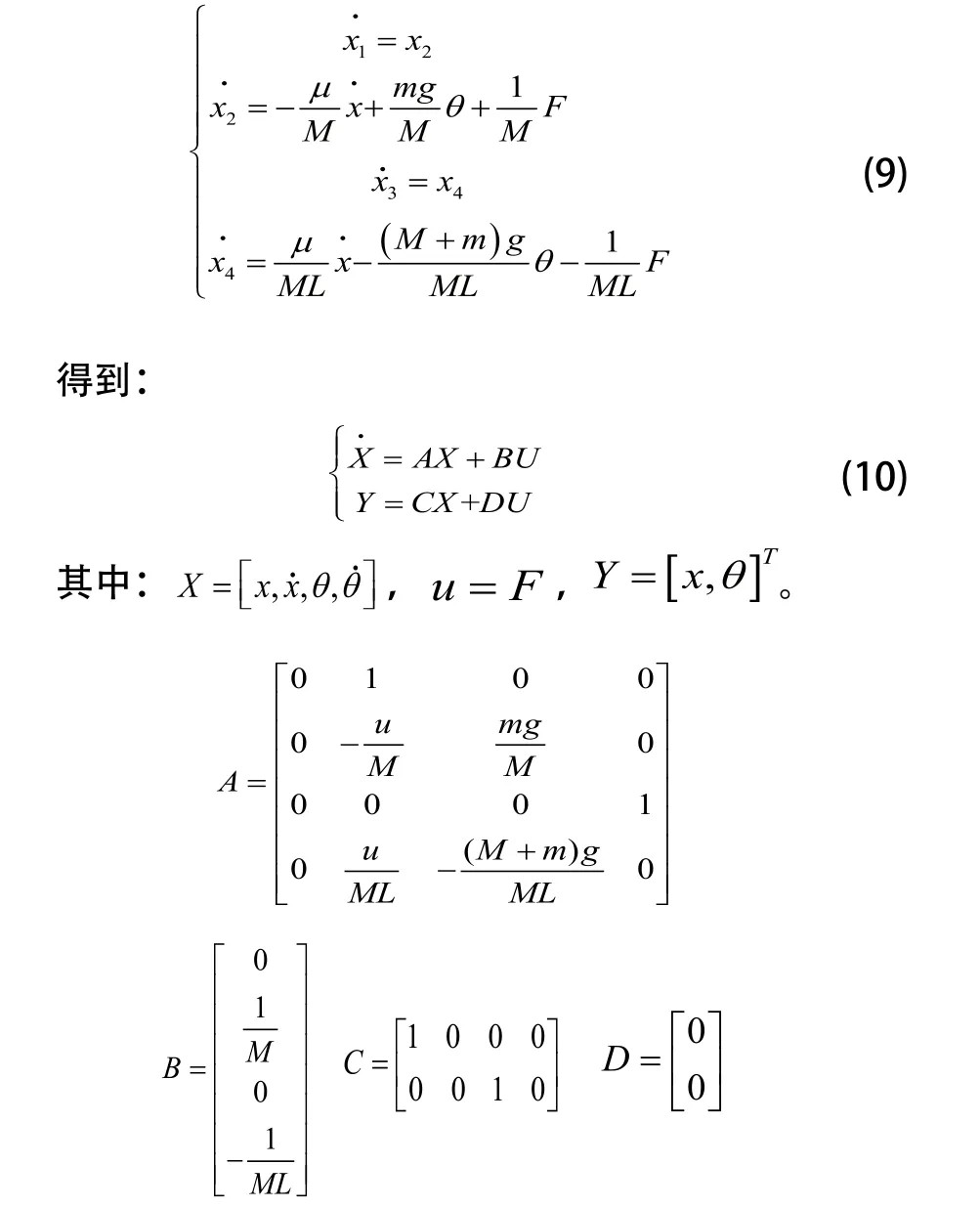
3 仿真研究

3.1 串级PID控制

利用前文中已经建立的桥式起重机的状态空间模型，在Matlab/Simulink中搭建起控制位置和摆角的串级PID防摇控制仿真模型如图3.1所示。

该控制模型的内环是对摆角进行控制，目的是控制摆角在0°左右，让吊重尽量在垂直方向上不晃动；外环是对小车位移的控制，控制小车准确地停靠在设定的位置。仿真结果如图3.2、3.3所示。

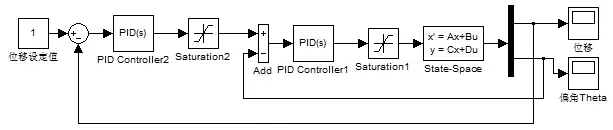
图2 串级PID控制

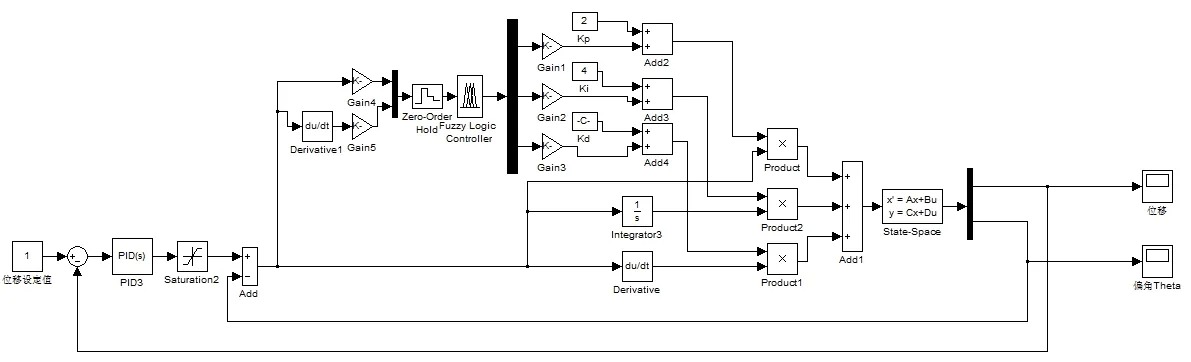
图3 模糊自适应PID控制

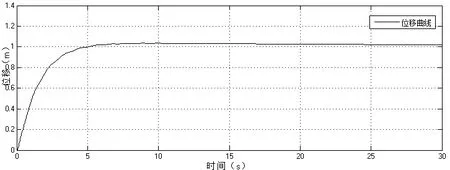
图4 位移曲线

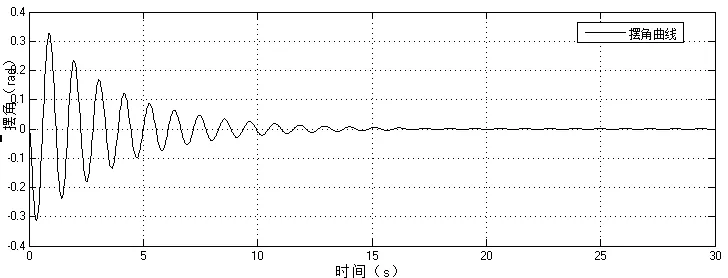
图5 摆角曲线

从以上图中可以看出，串级PID对位移的控制已经能达到较好的效果，但对摆角的控制并不理想，摆角的调节时间在t=18s左右，调节过程较长，摆角波动较大，不利于在实际生产中的应用。

3.2 串级模糊自适应PID控制

串级PID控制对摆角的控制不够理想，主要因为在运行过程中摆角受到小车速度、轨道间的摩擦力、风力等外界因素的干扰。模糊自适应PID控制是将PID控制与模糊控制两种控制方法相结合，发挥PID控制精度高和模糊控制灵活、适应性强的特点。

3.2.1 控制策略设计

针对串级PID控制的内环PID控制器主要是对摆角的控制，控制效果不甚理想。故提出将模糊控制算法引入内环的想法，控制策略为以进入内环的偏差信号e和偏差变化信号ec作为模糊控制器的输入变量，PID控制器的三个增量参数∆kp，∆ki，∆kd作为模糊控制器的输出变量。采用模糊推理的思想对PID控制器的三个参数进行在线整定，以使控制效果达到最优，建立仿真模型如图3.4所示。

建立Matlab仿真时，模糊控制器的输入输出变量均采用“负大”（NB），“负中”（NM），“负小”（NS），“零”（ZO），“正小”（PS），“正中”（PM），“正大”（PB）7个模糊集来表征，隶属函数都为三角形形式。如图3.5—3.10为各输入输出变量的隶属函数曲线。

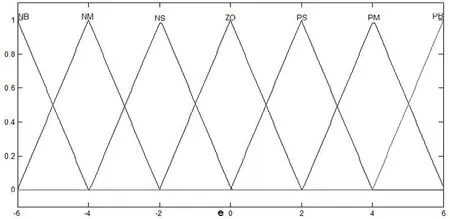
图6 输入偏差e的隶属函数曲线

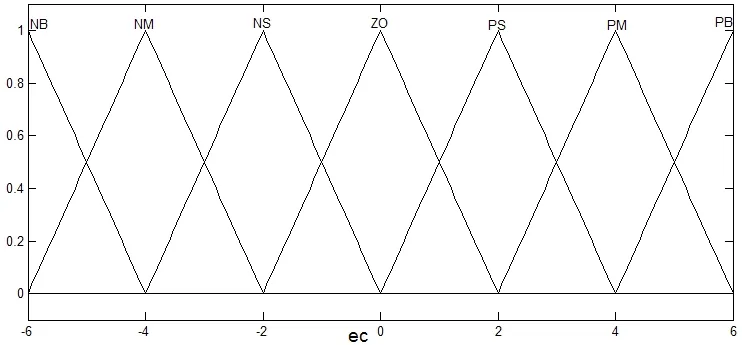
图7 输入偏差变化率ec的隶属函数曲线

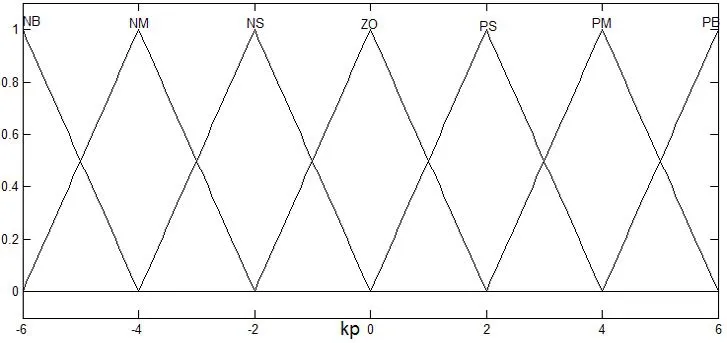
图8 输出∆kp的隶属函数曲线

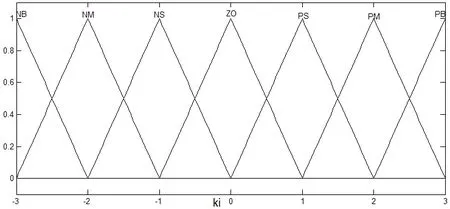
图9 输出∆ki的隶属函数曲线

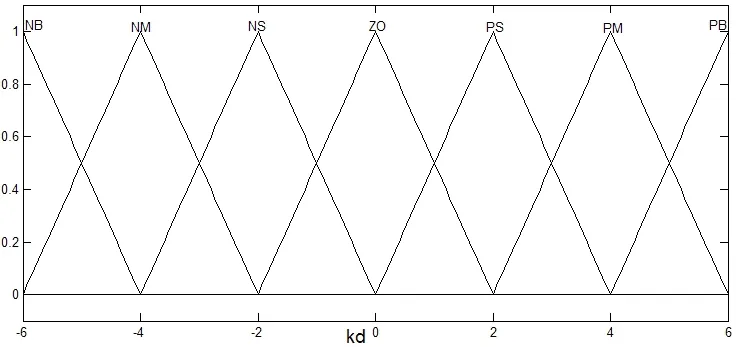
图10 输出∆kd的隶属函数曲线

3.2.2 模糊控制规则

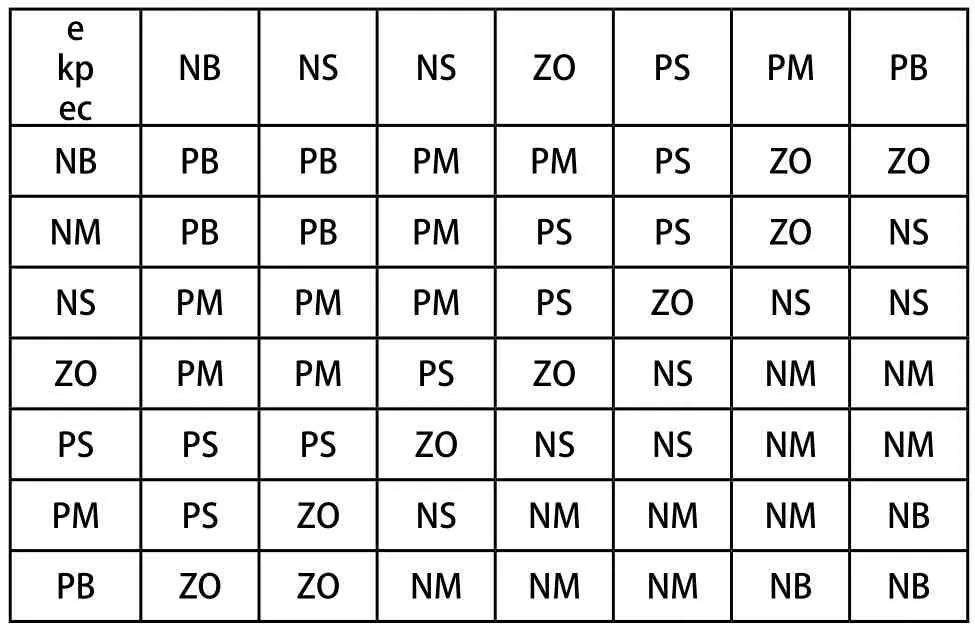
表1 比例增量参数的控制规则

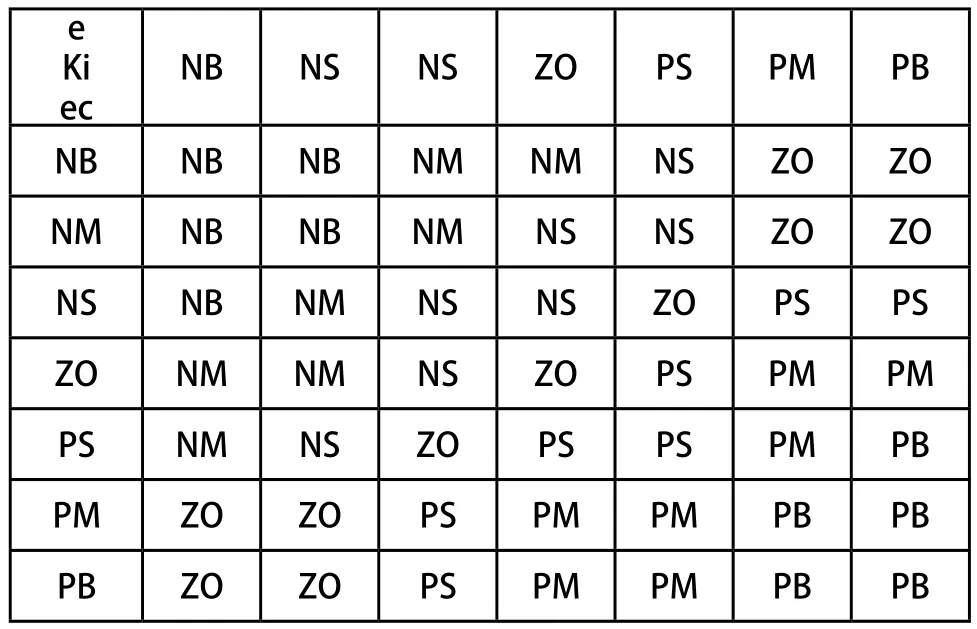
表2 积分增量参数∆ki的控制规则

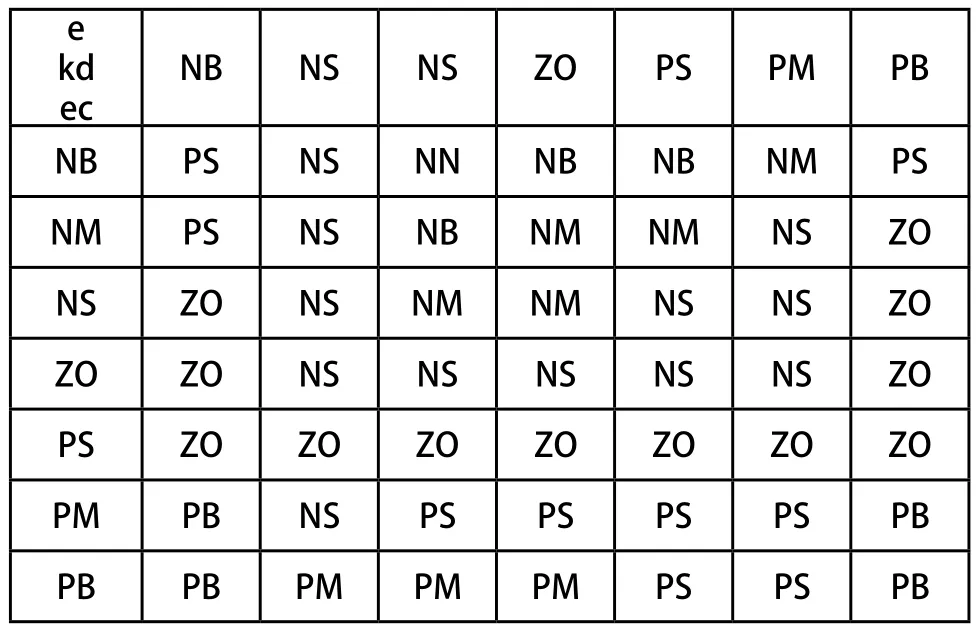
表3 微分增量参数∆kd的控制规则

3.2.3 仿真分析

在串级PID控制的基础上，内环引入模糊控制算法，通过∆kp，∆ki和∆kd三个增量参数分别对内环PID的比例、积分、微分参数进行自动的调节，实现PID参数的在线整定。对比仿真结果如图3.10、3.11所示。

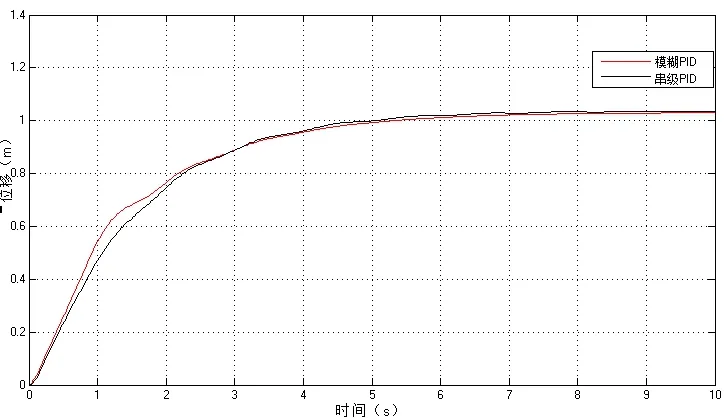
图11 位移曲线对比

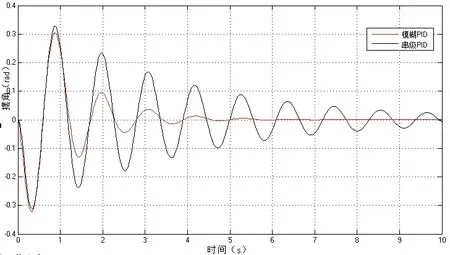
图12 摆角曲线对比

从图中可以看出，内环替换为模糊自适应PID控制后，对位移的控制没有太大的改变，但是对摆角的控制改善却明显，模糊自适应PID控制下摆角的波动明显减小，调节时间t=5s速度加快，摆角能够较快地稳定在0°左右。可见，改进后的串级模糊自适应PID的控制效果优于传统的串级PID的控制效果。

4 实验验证

前面已经从仿真研究上得出串级模糊自适应PID控制策略对小车速度和吊重摆角具有较好的控制效果，防摇效果明显，能够提高起重机的工作效率。为验证该控制算法在实际的工作中是否具有较优的防摇作用，本设计利用贝加莱的防摇控制系统实验平台进行了防摇控制实验。该实验平台主要由X20 PLC 及IO 模块，ACOPOSmicro 伺服驱动器，8LV 伺服电机及配套的电源模块等组成。防摇系统装置包括同步带直线导轨、负载小车和摆锤。实物如图4.1所示。

图13 贝加莱防摇控制平台

实验平台以X20PLC作为控制器，设计控制框图如图4.2所示。

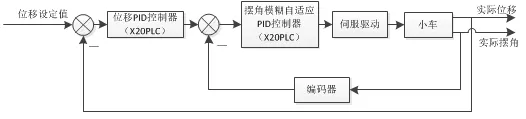
图14 控制系统框

在Matlab/Simulink中已安装的B&R Automation Studio Toolbox工具箱，将Simulink的仿真程序转换为C语言导入X20PLC直接运行，如图4.3所示。利用AS中的Trace套件记录摆角和位移的曲线，试验中考虑到实验平台的实际情况对参数和设定值都作出相应的调整，其中位移设定值s=40cm，通过实验得到一组摆角和位移的曲线如图4.4所示。

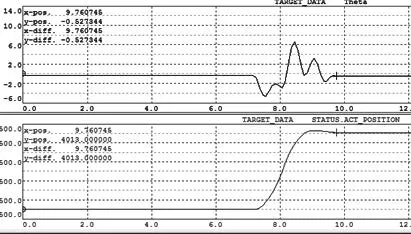
图16 实验曲线

分析实验曲线摆角最大在°以内，调节时间在2.5s左右，位移误差0.13cm。虽然与理论分析的结果有一定的出入，但是可以得出基于串级模糊自适应PID的控制系统对桥式起重机的吊重防摇系统具有较好的控制作用。

5 结论

本文基于拉格朗日方程建立桥式起重机的状态空间模型，利用Matlab/Simulink进行仿真研究，在传统串级PID控制的基础上提出将原来内环单纯的PID控制替换为模糊自适应PID控制，同时通过贝加莱防摇控制平台完成实验验证得出基于串级模糊自适应PID防摇控制系统的控制效果较好，对实际工业防摇控制系统的应用具有一定的指导作用。

参考文献：

[1] 徐军,汪伟刚.起重机防摇控制研究综述[J].造船技术,2013,(2):25-30.

[2] 王璐,常中龙,袁哲,et al.桥式起重机防摇控制系统数学建模方法研究[J].起重运输机械,2016,(9):1-5.

[3] 刘为,瞿军,袁湛,et al.龙门吊车防摇模糊控制研究[J].机械制造,2009,47(2):16-8.

[4] 单磊,费国.防摇控制系统在集装箱起重设备中的研究与应用[J].起重运输机械,2011,(10): 51-5.

[5] 胡艳丽,刘团结,季学斌,et al.基于模糊的的桥式起重机智能防摆控制研究[J].数字技术与应用,2014,14(7):22.

[6] 禹建丽,张宗伟,杨用增.基于自适应模糊神经网络的起重机吊摆防摇控制[J].电气自动化,2009,31(2):28-9.

[7] 王佳奕.岸边集装箱起重机自动防摇控制的研究[D].上海交通大学,2012.

Research on anti swing control of crane based on cascade fuzzy adaptive PID

LIU Bin1, CHEN Hai-yun1

TP273.4

：A