面向大规模数据属性效应控制的核心向量回归机
2017-09-15刘解放王士同邓赵红
刘解放 王士同 王 骏 邓赵红
1(江南大学数字媒体学院 江苏无锡 214122)2 (湖北交通职业技术学院交通信息学院 武汉 430079)
面向大规模数据属性效应控制的核心向量回归机
刘解放1,2王士同1王 骏1邓赵红1
1(江南大学数字媒体学院 江苏无锡 214122)2(湖北交通职业技术学院交通信息学院 武汉 430079)
(ljf-it@163.com)
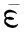
回归学习;属性效应控制;中心约束最小包含球;等均值约束;大规模数据
数据的可靠性是数据挖掘成败的关键因素之一.然而,由于科技水平制约、不同数据来源、系统误差、性别或种族歧视等原因,采集的数据(尤其是历史数据)往往存在对敏感属性的严重依赖[1-9].例如,早期的人口统计数据集(censusincome)[6-7]中,总的来说,女性工资远低于男性工资.类似该数据集中敏感属性(性别)所引起的数据严重偏差称为属性效应[8].它的存在严重影响学习器的训练和预测精度.因此,针对属性效应控制的问题引起了数据挖掘领域研究人员的广泛关注.
针对属性效应问题,研究人员从不同角度进行研究,提出了许多新的学习方法.早期研究中,人们大多在训练分类器前对数据进行预处理来移除敏感属性,从而达到移除数据之间依赖关系的目的.这些方法的局限性在于,它们只是对数据进行必要的预处理,而没有针对属性效应问题对已有的学习算法进行实质性的改进[2-5].文献[6]指出,由于多个相关属性的间接依赖,仅简单移除原始数据中的个别敏感属性并不能真正消除属性效应;另一方面,移除敏感属性会丢失部分有价值信息,这不利于后续学习器的训练.最近,研究人员大多通过改造已有的学习器来解决面向属性效应控制的分类和回归问题.例如,文献[6]通过向贝叶斯模型中添加隐变量,使用期望最大化学习准则来优化模型参数,提出了3种不同的贝叶斯分类学习方法.Kamishima等人[7]提出了适用于任意概率判别模型的正则化分类器,该方法通过向分类学习模型中引入正则化项来强制分类器使之独立于敏感属性,并进一步使用该方法解决了logistic回归问题.Kamiran等人[9]提出了基于决策树分类器,当选择非叶子节点特征时,该方法不但考虑关于目标的信息增益,而且考虑关于敏感属性的信息增益.这些方法较好地解决了针对属性效应控制的分类问题.针对回归问题,目前在该方面的研究成果较为少见,Calders等人[8]提出的等均值约束最小二乘(equalmeans-leastsquare,EM-LS)方法是线性回归中属性效应控制的典型代表.它基于误差最小化原则,通过对最小平方误差和目标学习准则施加等均值约束条件而实现.然而,由于它使用了矩阵乘法和求逆运算,时间和空间复杂度都达到O(N3),不但耗时且极易造成内存溢出,所以无法处理大规模数据的属性效应控制问题;另外,由于它采用了经验风险最小化原则,限制了它的泛化性和实用性.总之,这些方法虽然能够有针对性地解决属性效应在学习中的一些问题,但是仍然存在着局限性,主要表现在2个方面:1)算法复杂度较高,所以只适用于规模有限的数据集;2)大多面向属性效应控制的分类问题,对于非线性回归问题,却较少涉及.然而,在现实生活中诸如生物形态学和社会科学等各个领域,大规模非线性数据随处可见.如何面向复杂的大规模数据属性效应控制来进行非线性回归建模尚是学术研究的一个空白.
另一方面,基于最小包含球理论的大规模数据处理技术得到了深入的研究[10-12].该类方法通过求解近似最小包含球获得核心集,能够获得与原始输入数据集求解近似的结果且它的大小独立于原始输入数据集大小及样本维度,从而实现了大规模数据的压缩处理;此外,基于支持向量回归学习理论的非线性回归学习模型也得到了广泛的研究[13-14].该类方法通过将原特征空间中的数据映射到高维空间中,从而使非线性数据线性可分,并基于间隔最大化目标学习准则实现了非线性数据的回归学习.但是,支持向量学习技术均没有考虑属性效应对非线性回归学习性能的影响,因此不能直接用来解决针对属性效应控制的回归学习问题.
受上述思想的启发,本文将深入探讨面向大规模数据属性效应控制的非线性回归建模问题.首先,通过向支持向量回归机(supportvectorregression,SVR)目标学习准则中加入等均值约束条件提出了一种新型的非线性回归学习模型EM-SVR(equalmean-supportvectorregression)以解决训练数据中的属性效应问题.进一步,针对大规模数据属性效应控制的学习问题,通过将其与中心约束最小包含球建立等价关系,提出基于最小包含球的快速非线性回归建模方法FEM-CVR(fastequalmean-corevectorregression),并从理论上深入探讨相关性质.最后通过实验验证了本文方法的有效性.
1 等均值支持向量回归机算法EM-SVR
1.1 算法推导
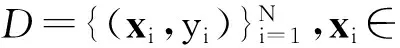
最小.通过引入L2范式的惩罚项和结构风险项,可构造并求解如下EM-SVR目标函数优化问题,
(1)
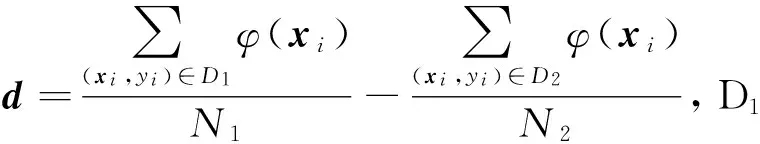
定理1. 对于式(1)的优化问题,其对偶问题可描述为如下的凸二次规划形式,
(2)
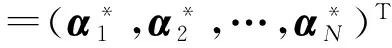
(3)
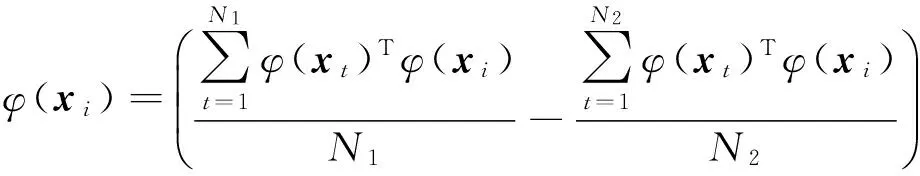
I为单位矩阵,1是元素为1的向量,带上标(*)的参数表示带上标*的参数或不带上标*的参数.

(4)
由KKT(Karush-Kuhn-Tucker)条件可得,
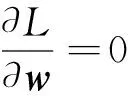
(5)
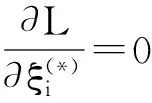
(6)
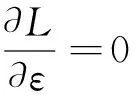
(7)
由式(5)和式(1)的等式约束条件wTd=0,可得:
(8)
将式(5)~(8)代入式(4),化简可得:
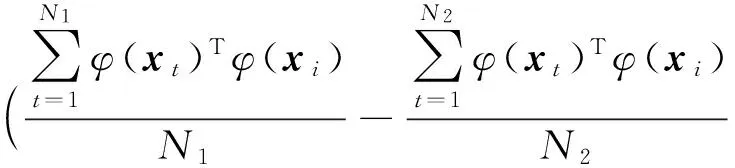
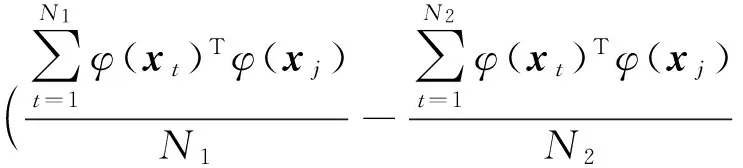
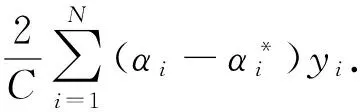
(9)
通过定义式(3),将式(9)写成对偶形式,也即得到式(2),因此,定理1成立.
证毕.
引理1[16]. 设X是d上的一个紧集,若H(xi,xj)是X×X上的连续对称函数且关于任意xi∈X的Gram矩阵半正定,则H(xi,xj)是Mercer核.
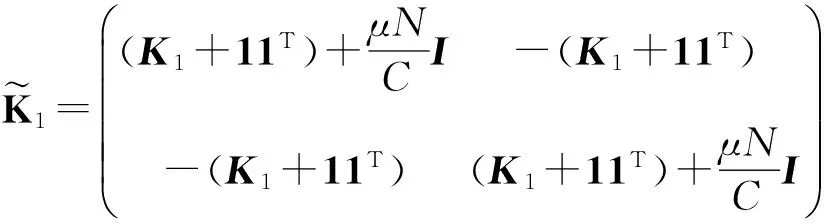
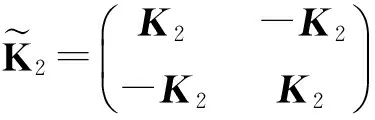
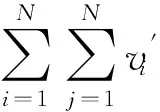
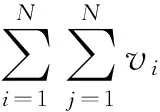
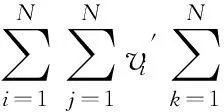
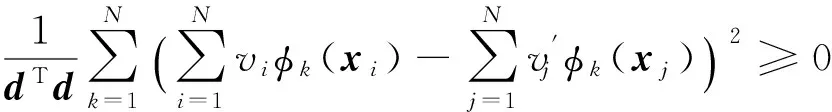
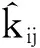
证毕.
根据定理1和定理2的推导,可得到等均值支持向量回归机算法EM-SVR,其主要步骤如下:
算法1. 等均值支持向量回归机算法EM-SVR.
输入:数据集D;
输出:拉格朗日乘子α(*).
步骤1.读入数据集D;
步骤3. 求解式(2)所示的二次规划(quadratic programming, QP)问题,解得拉格朗日乘子α(*);
步骤4. 把解得的α(*)带入式(5)和式(8),即可求出相应回归模型f(x)=wTφ(x).
1.2 时间复杂度分析
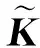
2 快速等均值核心向量回归机算法FEM-CVR
由于等均值约束条件的引入,EM-SVR可以很好地控制属性效应;核技巧的引入使之能够很好地解决非线性回归学习问题.但是在求解QP问题的过程中,其时间复杂度可达O((2N)3),因此面向大规模数据的属性效应控制,其处理效率低下.本文将其与中心约束最小包含球问题建立等价关系,提出了基于中心约束最小包含球CC-MEB理论的快速等均值核心向量回归机算法FEM-CVR.
2.1 最小包含球理论
MEB(minimumenclosingball)问题可描述为下列优化问题:
(10)
式(10)的对偶问题矩阵形式可以表示为
(11)
其中,K=(k(xi,xj))N×N=(φT(xi)φ(xj))N×N为核矩阵,φ为核空间映射函数,α=(α1,α2,…,αN)T为拉格朗日乘子,0=(0,0,…,0)T,1=(1,1,…,1)T.当核矩阵K对角线恒为常数k时,也即满足如式(12)时,
(12)
式(11)等价于式(13),
(13)
通过求解式(13),即可得到MEB的球心c和半径R,
(14)
Tsang等人[18]指出,形如式(13)并满足式(12)的QP问题等价于最小包含球问题.在此基础上,采用MEB理论的核心集方法开发了核心向量机(core vector machine, CVM)算法,研究表明,CVM算法对处理大规模数据集表现出非凡的效率.
Tsang等人[17]对核心向量机进行了扩展,提出广义核心向量机(generalized core vector machine, GCVM).对形式如式(11)的QP问题,即使所含的一次项不满足式(12),也可使用核心集技术进行快速求解,同时提出中心约束最小包含球CC-MEB来解决这一问题.
在CC-MEB中,给核空间任意样本点φ(xi)增加一维新特征δi∈,形成新特征空间的新样本点(φ(xi),δi)T,并约束MEB中增加的新特征维对应的球心定为圆点,即CC-MEB的中心是(c,0)T,这里c是原特征空间的MEB球心,然后求解新特征空间的MEB问题.CC-MEB目标问题可描述为下列优化问题:
(15)
式(15)的对偶问题矩阵形式可表示为,
(16)
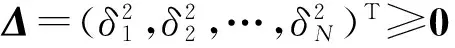
(17)
此外,任意点(φ(xi),δi)T到球心(c,0)T的距离可表示为

(18)
因为αT1=1,所以在式(16)的目标函数中增加任意一项-ηαT1,η∈,不会影响其最优解,于是,式(16)等价于式(19),
(19)
文献[17]指出,任意满足式(19)的QP问题都可认为是CC-MEB问题,可运用核心集技术进行快速求解.
2.2 FEM-CVR算法
(20)
其中,η为任意实数并保证Δ≥0.根据式(20),式(2)随即等价于式(21),
(21)
显然,式(21)满足式(19)的形式和约束条件,因此,它的QP问题可视为CC-MEB问题,也即EM-SVR可视为是CC-MEB问题,即可用核心集快速算法求解.
根据前面的推导,可得到快速等均值核心向量回归机算法FEM-CVR,其主要步骤如下:
算法2. 快速等均值核心向量回归机算法FEM-CVR.
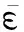
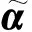
步骤1. 设t为迭代计数器,且初值为0,并初始化核心集CS0,最小包含球球心c0,半径R0;
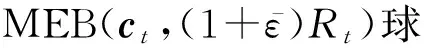
步骤3. 根据式(18)查找离球心ct最远的样本点x,并添加该点到核心集CSt+1=CSt∪{x};
步骤4. 根据式(21)求解新的CC-MEB,记为MEB(CSt+1),并且通过式(17)设定ct+1=cMEB(CSt+1),Rt+1=RMEB(CSt+1);
步骤5.t=t+1,并返回步骤2;
步骤6. 终止训练,返回所需要的输出.
在实现FEM-CVR算法时有2点需要说明:
1)步骤1的初始化问题.已有研究表明[17-19],合理选择数据点来初始化核心集可有效提高算法的性能.本文中,我们采用如下方法:首先从原始输入数据集D中任取一点x,再选一点xa,使其距离x最远;然后再找一点xb,使其距离xa最远.最终初始化核心集为CS0={xa,xb},继而球心为c0=(xa+xb)2,半径为2.
2) 步骤2和步骤3中涉及的距离计算问题.对于每次迭代,就N个训练点来说,计算式(18)要花费时间为O(|CSt|2+(N-|CSt|)|CSt|)=O(N×|CSt|),当N非常大时,计算量巨大.因此,可以使用概率加速方法[12,17],其思想在时间复杂度分析中有详细说明.
2.3 时间复杂度分析
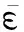
对于1.1节中提出的EM-SVR,需要求解其对偶的QP问题,所以它的运行时间不小于O((2N)2.3),甚至达到O((2N)3),而空间复杂度为O((2N)2).比较而言,FEM-CVR在训练过程中的时间及空间复杂度都具有明显的优势.
FEM-CVR算法是基于最小包含球近似算法的一个特例,因此在计算系统开销时,关于最小包含球核心集的结论同样适合FEM-CVR算法.本文根据文献[11,17,19],给出如下性质:
性质1指出了FEM-CVR算法在最坏情况下的理论迭代次数;性质2指出了FEM-CVR算法在最坏情况下的理论运行时间,它与数据集大小N呈线性关系.实际上,我们在实践中发现,在面向大规模数据属性效应控制时,算法的真实迭代次数和运行时间远低于理论最坏值,这也表明了FEM-CVR算法对大规模数据集处理的优势.
3 实验结果与分析
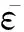
本文实验采用如下3种指标对不同算法所得回归结果进行比较.
1) 均方根误差(root mean square error,RMSE)指标[17]:
(22)其中,yi为第i个样本的真实值,N为所有样本个数.
2) 平均差(mean difference,MD) 指标[8]:
(23)
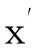
3) 曲线下面积(area under the ROC curve,AUC)指标[8]:
(24)
其中,I(·)是指标函数,当它的参数为真时,返回1,否则为0.AUC的变化范围为[0,1],当AUC=0.5时,表示随机预测或不存在属性效应.
3.1 FEM-CVR,EM-LS,SVR的比较
我们首先基于Communities and Crime[8]与Wine Quality[21]两个数据集对本文算法进行评估,它们是数据挖掘领域公认的突显属性效应的2个典型数据集.
Communities and Crime数据集包含社区及社区犯罪率的社会经济信息.本实验中,我们对数据集进行了预处理,删除了含有空值的属性,并根据二值敏感属性Race把数据集分为2组:1)表示由全体黑人形成的社区;2)表示由全体非黑人形成的社区.并对所有属性进行标准化.在最终得到的数据集中,Communities and Crime数据集总共包含1994个实例,其中黑人社区和非黑人社区分别包含970和1 024个样本,该数据集共有99个属性.对该数据集进行分析,我们发现该数据集体现了目标犯罪率Crime Rate和敏感属性Race之间的强烈依赖关系.黑人社区平均犯罪率为0.35,而非黑人社区平均犯罪率为0.13(MD=0.22,AUC=0.79).表1给出了Communities and Crime数据集的相关信息.
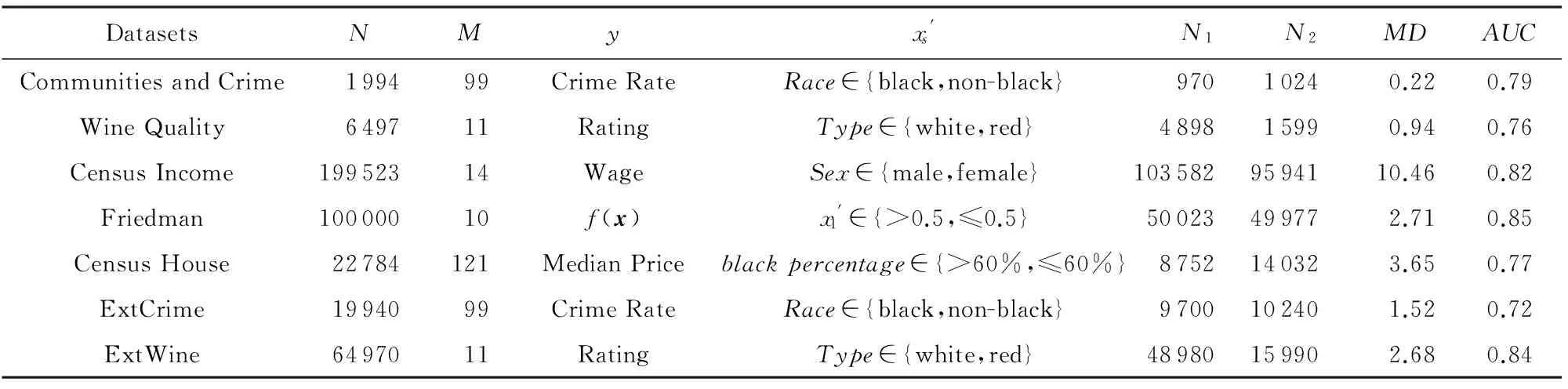
Table 1 The Main Characters of Each Dataset
Wine Quality数据集包含了对红酒和白酒评级Rating的描述.含有11个属性特征,函数输出描述了对酿酒品质的评级,取值范围为[1,10].实验中我们对数据进行归一化预处理.原始数据集中,2类酒的评级平均差较小.为了方便观察试验结果,我们随机选取了70%的白酒数据,在它们的评级上加1.修改后红酒和白酒2类数据的MD=0.94,AUC=0.76.数据集的相关信息如表1所示.
我们参考了文献[8]中的方法采用倾向评分分析(propensity score analysis, PSA)[22]对数据进行分层.基于以上2个数据集,我们分别运行EM-LS,SVR,FEM-CVR三个算法对分层后得到的每一层数据进行建模.图1和图2给出了算法的运行结果,它们均由十折交叉验证得到.仿照文献[8]中的命名方法,我们对各算法在分层数据上进行建模采用后缀“-M”进行标识.

Fig. 1 Experimental results on Communities and Crime dataset图1 Communities and Crime数据集实验结果
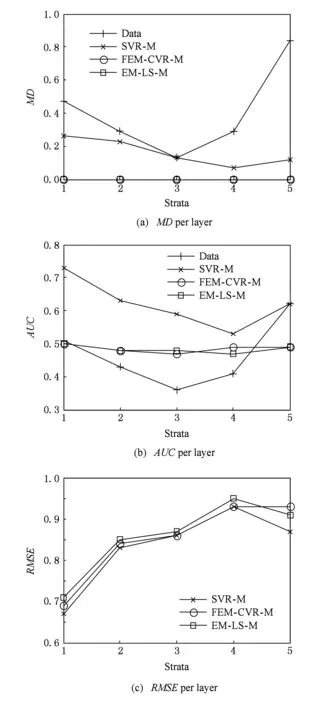
Fig. 2 Experimental results on Wine Quality dataset图2 Wine Quality数据集实验结果
图1和图2分别给出了分层后每层MD,AUC和RMSE.为了便于比较,在图1(a)(b)和图2(a)(b)中我们还给出原始输入数据集的每层MD和AUC.如图1(a)(b)和图2(a)(b)所示,每层中犯罪率对敏感属性种族的依赖和酒品等级评定对酒类型的依赖都显著降低.
从图1和图2中不难发现,本文引入等均值约束是有效的,它能够使每层的MD值几乎为0,AUC值接近0.5,也即几乎完全消除了属性效应.而SVR没有考虑属性效应,所以它的MD值略大,而AUC值也趋向于0或1,表明SVR不但不具有属性效应控制能力,甚至可能放大属性效应.此外,基于图1(c)和图2(c)来考察均方根误差,本文的FEM-CVR由于采用了非线性回归模型,其拟合效果明显优于EM-LS方法.因此,基于图1和图2我们不难发现FEM-CVR较SVR和EM-LS提供了更好的属性效应控制效果.
表2进一步比较了3种回归方法采用不同的模型得到的结果.我们分全局模型(相应的方法采用“-S”进行标识,如SVR-S,EM-LS-S,FEM-CVR-S)和分层模型(如SVR-M,EM-LS-M,FEM-CVR-M)两种情况进行对比.从表2中我们发现其结果类似图1和图2.SVR没有考虑属性效应,如2个数据集上SVR-S中AUC的值都大于原始数据集的AUC,所以增大了数据偏差,获得了较差的结果.由于等均值约束的引入,EM-LS和FEM-CVR均能较好地消除数据集的属性效应,但是EM-LS由于是线性回归模型,所以得到的回归结果不令人满意.而FEM-CVR在施加等均值约束后,仍然能够获得相对较小的均方根误差.需要说明的是:为了消除数据属性效应(数据偏差),我们施加了等均值约束条件,此条件表示2组的预测结果应该相近;因此,其必定导致误差加大.这也是SVR的均方根误差小于其他2个算法的原因,但其不具有属性效应控制能力.
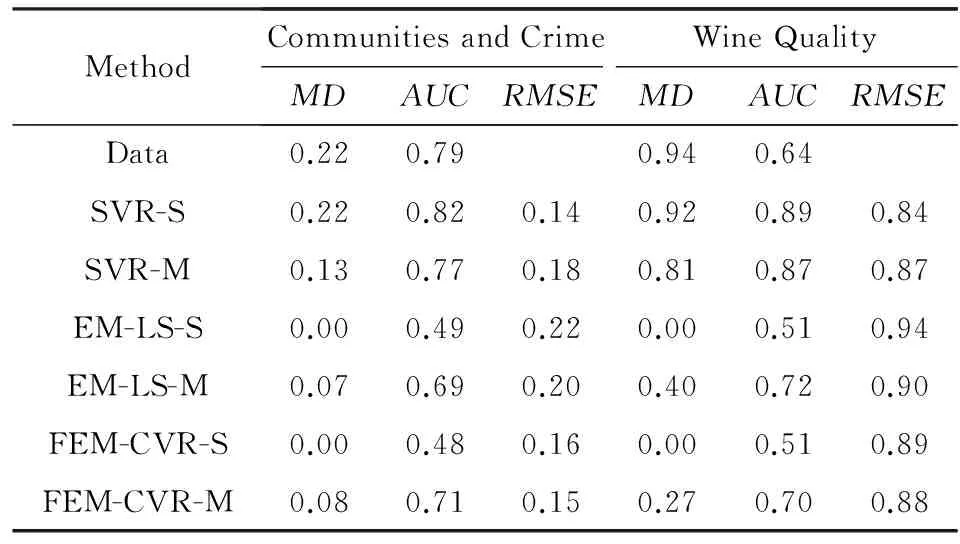
Table 2 Comparison of Experimental Results for Different
3.2 大规模数据环境实验
为了进一步验证大规模数据属性效应环境下FEM-CVR的性能,我们基于文献[10]的方法对Communities and Crime和Wine Quality数据集进行了扩充.扩充后的新数据集每个属性的随机偏移量服从正态分布N(0,1),从而构造出大规模数据集,扩充后的Communities and Crime数据集记为ExtCrime,样本数为19 940,Wine Quality数据集记为ExtWine,样本数为64 970.另外,新增加了2个UCI数据集Census Income[6-7]及Census House[23]和1个合成数据集Friedman[24].表1显示了这些数据集的主要特征.
Census Income数据集抽取于人口普查数据.该数据集被认为关于敏感属性性别Sex存在属性效应,总的说来,女性的工资远低于男性工资.Census Income数据集原本用于分类,根据个人信息(如职业、性别、学历等属性)预测个人工资是否大于5万美金.本文删除个别空值数据及属性值较少的字符属性,并且离散化所有字符属性,然后随机生成连续的目标工资.修改后的数据集,男性工资与女性工资平均差MD=10.46,曲面下面积AUC=0.82.
Census House数据集是由美国统计局提供的房屋调查数据,它基于某地区的人口结构和房屋市场预测房子的平均价.Friedman是1个合成数据集.Census House和Friedman这2个数据集偏差并不明显.为了方便观察试验结果,通过采用3.1节处理Wine Quality数据集相同的方法放大它们的属性效应,处理后的数据集主要特征如表1所示.
为了验证FEM-CVR能够有效处理针对大规模数据属性效应控制的回归问题,我们首先从Census House数据集中分别随机抽取不同容量的子集,分别运行EM-LS,SVR,FEM-CVR,并采用十折交叉验证,对比它们的CPU运行时间、支持向量个数(SV)和均方根误差.
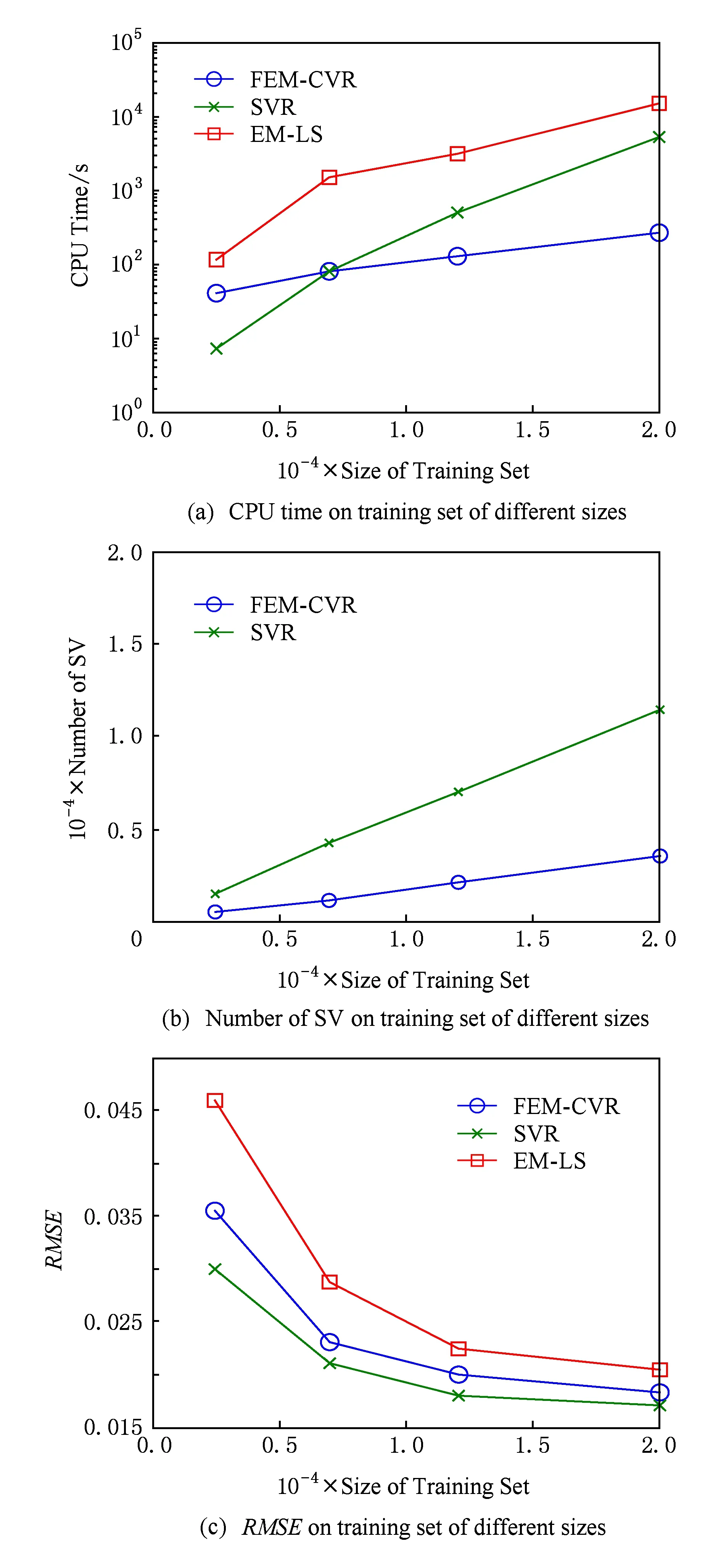
Fig. 3 Experimental results on Census House dataset图3 Census House数据集实验结果
图3(a)显示,训练样本个数较少时,FEM-CVR在求解核心集过程中需要迭代外扩(多次求解QP问题),所以其速度优势表现不明显,甚至其运行速度低于SVR;但是随着样本个数的增多,采用基于最小包含球的核心集进行优化求解的速度优势得到了充分的体现,其时间复杂度与训练样本个数基本呈线性关系,明显优于同样具有处理属性效应能力的EM-LS算法.
图3(b)显示,采用不同大小的样本容量训练时,SVR选择大约60%样本作为的支持向量;而FEM-CVR的支持向量数目远低于SVR.较少的支持向量个数有助于减少运行时间.
图3(c)显示,FEM-CVR可以取得与SVR接近的均方根误差,其值明显小于同样具有处理属性效应能力的EM-LS算法.
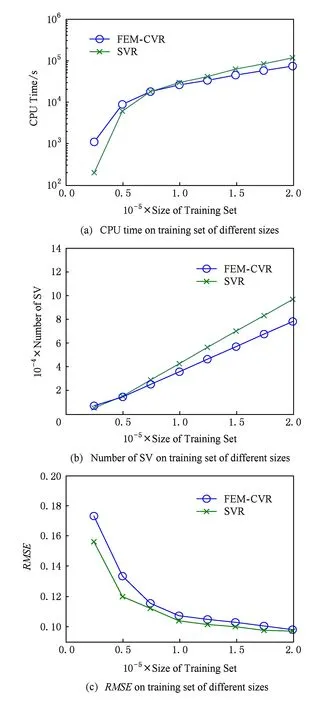
Fig. 4 Experimental results on Census Income dataset图4 Census Income数据集实验结果
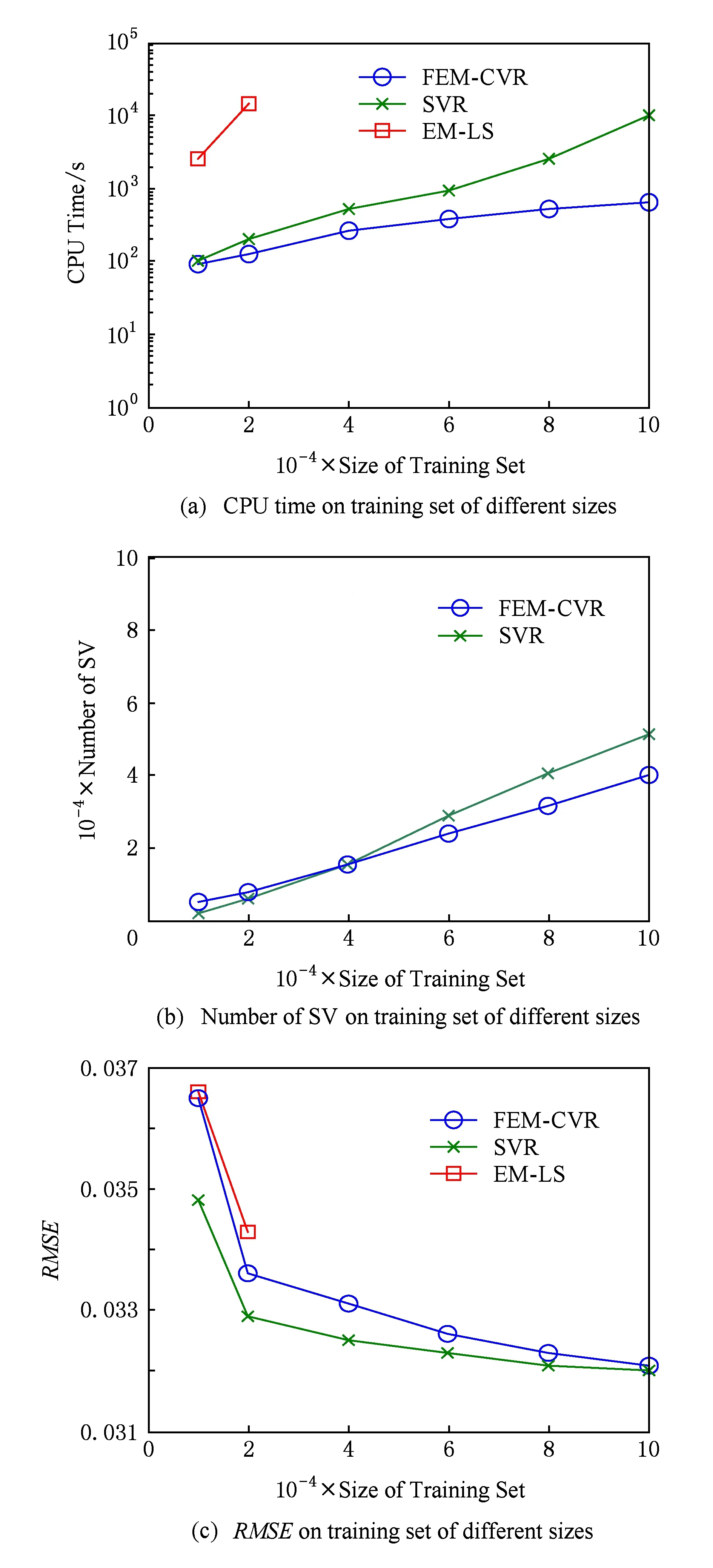
Fig. 5 Experimental results on Friedman dataset图5 Friedman数据集实验结果
采用相同的实验策略,我们在Census Income,Friedman,ExtCrime和ExtWine数据集上进行了与上文相同的实验,图4~7给出了相应的实验结果.通过观察可以发现这些结果表现出类似上文的特征.需要说明的是EM-LS算法在训练数据集大于20 000时,内存溢出,我们无法给出结果;小于20 000时,CPU运行时间也明显高于FEM-CVR,这充分说明了EM-LS算法在处理大规模数据回归问题方面的不足.另外,表3给出了分别选取Census Income和Census House数据集中10 000个样本时,FEM-CVR最大选择了不足2 000多个核心向量.核心向量的减少,致使支持向量的减少,从而加快了运行速度.
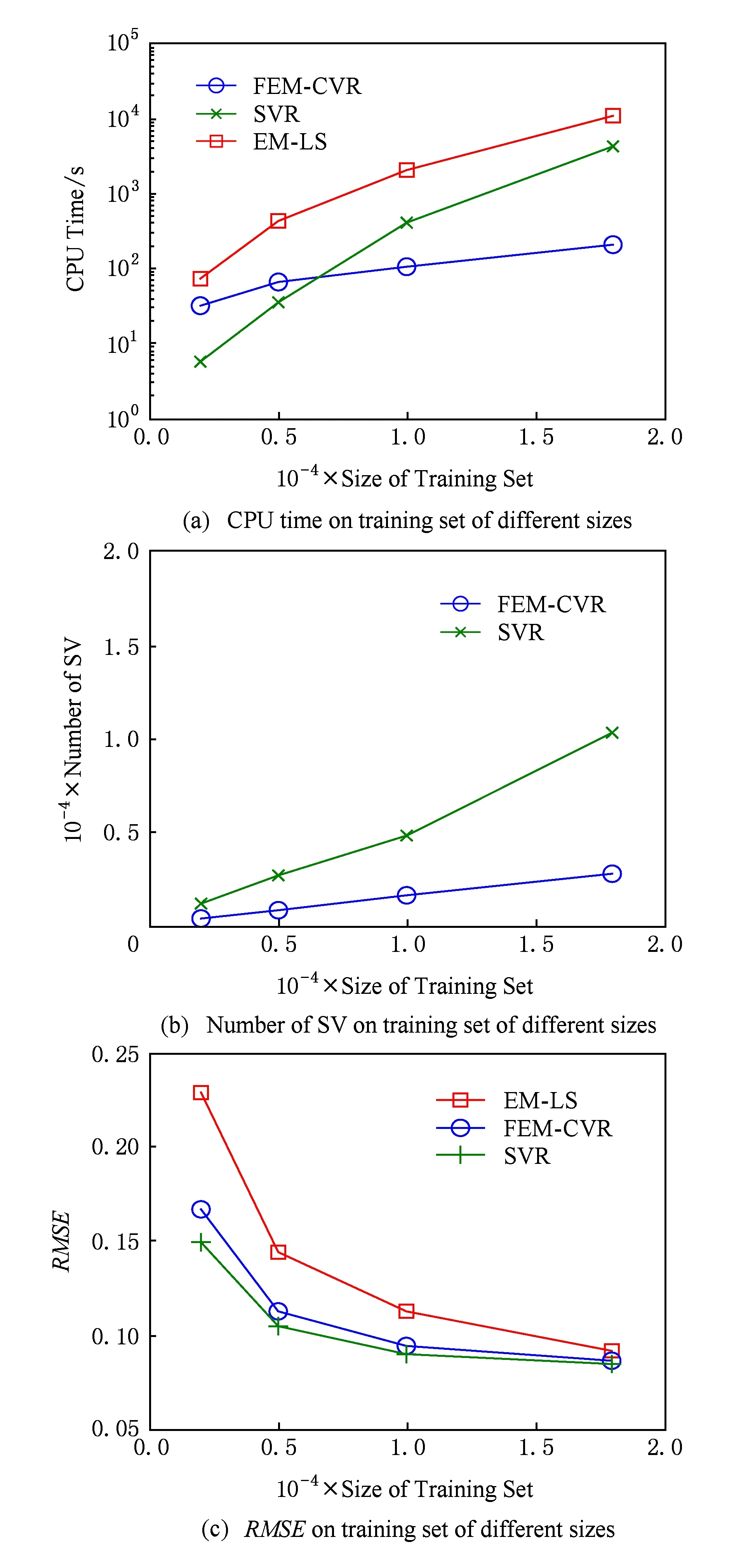
Fig. 6 Experimental results on ExtCrime dataset图6 ExtCrime数据集实验结果
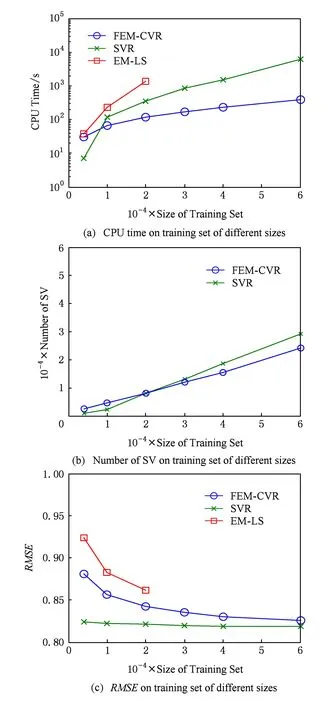
Fig. 7 Experimental results on ExtWine dataset图7 ExtWine数据集实验结果
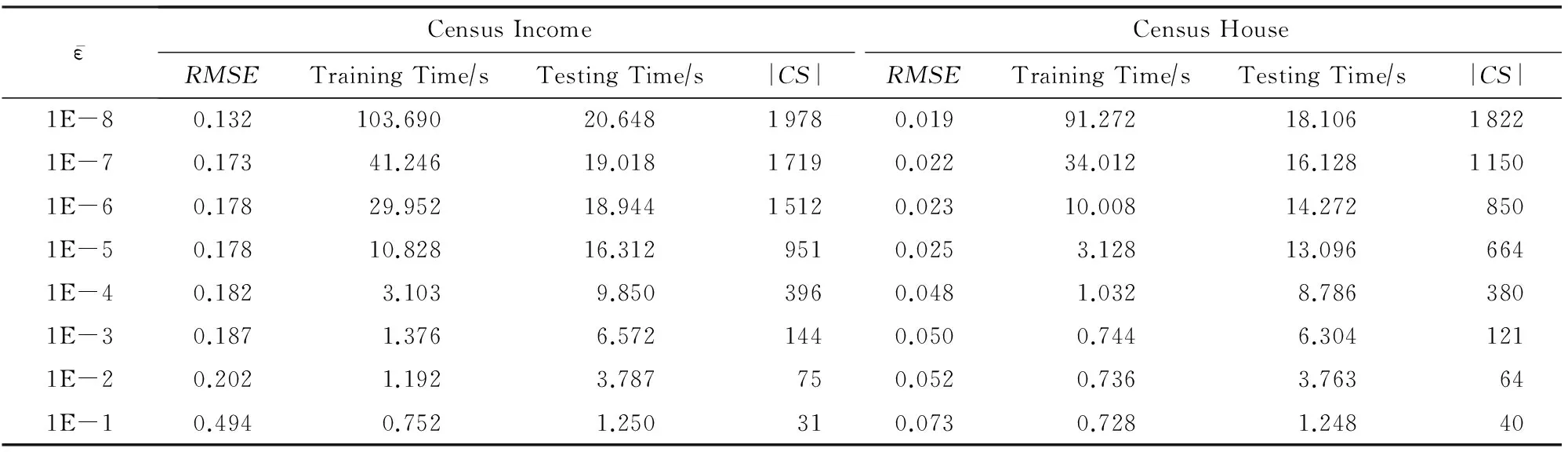
ε-CensusIncomeCensusHouseRMSETrainingTime∕sTestingTime∕s|CS|RMSETrainingTime∕sTestingTime∕s|CS|1E-80.132103.69020.64819780.01991.27218.10618221E-70.17341.24619.01817190.02234.01216.12811501E-60.17829.95218.94415120.02310.00814.2728501E-50.17810.82816.3129510.0253.12813.0966641E-40.1823.1039.8503960.0481.0328.7863801E-30.1871.3766.5721440.0500.7446.3041211E-20.2021.1923.787750.0520.7363.763641E-10.4940.7521.250310.0730.7281.24840
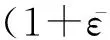
4 结 论
[1]Pedreshi D, Ruggieri S, Turini F. Discrimination-aware data mining[C]Proc of the 14th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2008: 560-568
[2]Calders T, Kamiran F, Pechenizkiy M. Building classifiers with independency constraints[C]Proc of the 9th IEEE Int Conf on Data Mining Workshops. Piscataway, NJ: IEEE, 2009: 13-18
[3]Kamiran F, Calders T. Classifying without discriminating[C]Proc of the 2nd Int Conf on Computer, Control & Communication (IC4). Piscataway, NJ: IEEE, 2009: 1-6
[4]Kamiran F, Calders T. Classification with no discrimination by preferential sampling[C]Proc of the 19th Annual Machine Learning Conf of Belgium and the Netherlands. Leuven, Belgium: DTAI, 2010: 1-6
[5]Pedreschi D, Ruggieri S, Turini F. Measuring discrimination in socially-sensitive decision records[C]Proc of the SIAM Int Conf on Data Mining. New York: ASA, 2009: 581-592
[6]Calders T, Verwer S. Three Naive Bayes approaches for discrimination-free classification[J]. Data Mining and Knowledge Discovery, 2010, 21(2): 277-292
[7]Kamishima T, Akaho S, Asoh H, et al. Fairness-aware classifier with prejudice remover regularizer[C]Proc of the Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, 2012: 35-50
[8]Calders T, Karim A, Kamiran F, et al. Controlling attribute effect in linear regression[C]Proc of the 13th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2013: 71-80
[9]Kamiran F, Calders T, Pechenizkiy M. Discrimination aware decision tree learning[C]Proc of the 10th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2010: 869-874
[10]Ying Wenhao, Xu Min, Wang Shitong. Fast adaptive clustering by synchronization on large scale datasets[J]. Journal of Computer Research and Development, 2014, 51(4): 707-720 (in Chinese)(应文豪, 许敏, 王士同. 在大规模数据集上进行快速自适应同步聚类[J]. 计算机研究与发展, 2014, 51(4): 707-720)
[11]Xu Min, Wang Shitong, Gu Xin, et al. Support vector regression for large domain adaptation[J]. Journal of Software, 2013, 24(10): 2312-2326 (in Chinese)(许敏, 王士同, 顾鑫, 等. 大样本领域自适应支撑向量回归机[J].软件学报, 2013, 24(10): 2312-2326)
[12]Wang Jun, Wang Shitong, Deng Zhaohong. Fast kernel density estimator based image thresholding algorithm for small target images[J]. Acta Automatica Sinica, 2012, 38(10): 1679-1689 (in Chinese)(王骏, 王士同, 邓赵红. 面向小目标图像的快速核密度估计图像阈值分割算法[J]. 自动化学报, 2012, 38(10): 1679-1689)
[13]Ding Lizhong, Liao Shizhong. KMA-α: A kernel approximation algorithm for support vector machines[J]. Journal of Computer Research and Development, 2012, 49(4): 746-753 (in Chinese)(丁立中, 廖士中. KMA-α:一个支持向量机核矩阵的近似计算算法[J]. 计算机研究与发展, 2012, 49(4): 746-753)
[14]Wang Zhen, Shao Yuanhai, Bai Lan, et al. Twin support vector machine for clustering[J]. IEEE Trans on Neural Networks and Learning Systems, 2015, 26(10): 2583-2588
[15]Schölkopf B, Bartlett P, Smola A, et al. Support Vector Regression with Automatic Accuracy Control[M]. Berlin: Springer, 1998: 111-116
[16]Zhang Jingxiang, Wang Shitong. Common-decision-vector based multiple source transfer learning classification and its fast learning method[J]. Acta Electronica Sinica, 2015, 43(7): 1349-1355 (in Chinese)(张景祥, 王士同. 基于共同决策方向矢量的多源迁移及其快速学习方法[J]. 电子学报, 2015, 43(7): 1349-1355)
[17]Tsang I, Kwok J, Zurada J. Generalized core vector machines[J]. IEEE Trans on Neural Networks, 2006, 17(5): 1126-1139
[18]Tsang I, Kwok J, Cheung P. Core vector machines: Fast SVM training on very large data sets[J]. Journal of Machine Learning Research, 2005, 6(1): 363-392
[19]Deng Zhaohong, Chung Fulai, Wang Shitong. FRSDE: Fast reduced set density estimator using minimal enclosing ball approximation[J]. Pattern Recognition, 2008, 41(4): 1363-1372
[20]Chang C C, Lin C J. LIBSVM: A library for support vector machines[J]. ACM Trans on Intelligent Systems and Technology, 2011, 2(3): 27
[21]Cortez P, Cerdeira A, Almeida F, et al. Modeling wine preferences by data mining from physicochemical properties[J]. Decision Support Systems, 2009, 47(4): 547-553
[22]Rosenbaum P R, Rubin D B. Reducing bias in observational studies using subclassification on the propensity score[J]. Journal of the American Statistical Association, 1984, 79(387): 516-524
[23]Musicant D R, Feinberg A. Active set support vector regression[J]. IEEE Trans on Neural Networks, 2004, 15(2): 268-275
[24]Wang Shitong, Wang Jun, Chung F L. Kernel density estimation, kernel methods, and fast learning in large data sets[J]. IEEE Trans on Cybernetics, 2014, 44(1): 1-20

Liu Jiefang, born in 1982. PhD candidate at the School of Digital Media, Jiangnan University. Member of CCF. His main research interests include pattern recognition, intelligent computation.

Wang Shitong, born in 1964. Professor, PhD supervisor at the School of Digital Media, Jiangnan University. His main research interest include artificial intellig-ence, pattern recognition and bioinformatics.

Wang Jun, born in 1978. PhD, associate professor, master supervisor at the School of Digital Media, Jiangnan University. Senior member of CCF. His main research interests include pattern recognition, data mining, and digital image processing.

Deng Zhaohong, born in 1981. PhD, professor, master supervisor at the School of Digital Media, Jiangnan University. Senior member of CCF. His main research interests include fuzzy modeling and intelligent computation.
Core Vector Regression for Attribute Effect Control on Large Scale Dataset
Liu Jiefang1,2, Wang Shitong1, Wang Jun1, and Deng Zhaohong1
1(SchoolofDigitalMedia,JiangnanUniversity,Wuxi,Jiangsu214122)2(SchoolofTransportationandInformation,HubeiCommunicationsTechnicalCollege,Wuhan430079)
regressionlearning;attributeeffectcontrol;centerconstrained-minimumenclosingball(CC-MEB);equalmeanconstraint;largescaledata
2016-07-13;
2016-12-09
国家自然科学基金项目(61300151,61572236);江苏省杰出青年基金项目(BK20140001);江苏省自然科学基金项目(BK20130155,BK20151299) This work was supported by the National Natural Science Foundation of China (61300151, 61572236), the Distinguished Youth Foundation of Jiangsu Province (BK20140001), and the Natural Science Foundation of Jiangsu Province (BK20130155, BK20151299).
TP391
