基于天文辅助的弹载双惯组空中传递对准方案

祝佳芳， 王新龙， 李群生， 王 盾

(1. 北京航空航天大学 宇航学院， 北京 100191； 2. 北京航空航天大学 仪器科学与光电工程学院， 北京 100191； 3. 天地一体化信息技术国家重点实验室， 北京 100191)

基于天文辅助的弹载双惯组空中传递对准方案

祝佳芳1， 王新龙1， 李群生2， 王 盾3

(1. 北京航空航天大学 宇航学院， 北京 100191； 2. 北京航空航天大学 仪器科学与光电工程学院， 北京 100191； 3. 天地一体化信息技术国家重点实验室， 北京 100191)

提出一种基于天文辅助的弹载双惯组空中传递对准方案。 针对弹道导弹大部分时间飞行在大气层外的特点， 引入天文导航系统对主INS进行辅助， 使得主INS能长时间保持在较高精度； 在充分考虑弹体挠曲变形的情况下， 建立了双惯组空中传递对准模型。 根据模型中各状态量的可观测程度分析结果， 得到原有传递对准模型的降阶模型。 采用“姿态+速度”匹配算法， 估算和补偿了子INS导航参数误差以及器件误差。 仿真结果表明， 提出的对准方案不仅能长时间保证主INS精度， 还可以有效改善子INS的对准精度。

天文导航; 传递对准； 双惯组； 可观测性分析

0 引 言

惯性导航系统(简称惯导)具有自主导航的特点， 在弹道导弹的导航工作中得到广泛应用[1]。 然而， 由于惯性测量精度受到器件水平的限制， 惯导的误差随时间发散。 目前， 解决这一问题的有效途径主要包括组合导航和传递对准。

传递对准一般要求两个惯导固连在导弹上但位置却不完全重合， 其中， 精度较高的惯导称为主惯导(主INS)， 通常装载在弹体上； 而精度较低的称为子惯导(子INS)， 一般装在导弹的弹头上。 传递对准通过引入高精度主INS的信息， 利用卡尔曼滤波校正和补偿子INS误差[2]。 根据弹道导弹飞行特点， 弹载双惯组传递对准主要有以下三个特点：(1)飞行时间长， 高度高， 射程远。 一般中程弹道导弹的射程在2 000～5 000 km， 需要的飞行时间长， 射击高度高。 这就要求主INS在长时间内保持一定的精度。 (2)机动受到限制。 弹道导弹通常沿着一条预定的弹道飞行， 因此导弹的机动方式受到限制[3]。 这将导致传递对准过程中一些状态量的可观测度较低。 如果将其引入滤波反馈， 不仅会使滤波收敛时间变长， 还可能导致滤波发散。 因此有必要对系统状态量的可观测度进行分析[4]。 (3)打击精度要求高。 除惯性器件本身精度外， 传递对准精度是决定导弹射击精度的一项重要因素， 而传递对准精度与对准模型有着密切的关系。 如果在建模过程中充分考虑弹体挠曲变形， 那么传递对准的精度将得到极大的提高[5]。

基于此， 提出了一种基于天文导航辅助的高精度弹载双惯组空中传递对准方案， 在保证主INS精度的前提下， 使子INS精确地对准主INS， 从而达到提高弹道导弹打击精度的目的。

1 基于天文辅助的弹载双惯组空中传递对准方案设计

基于天文辅助的弹载双惯组传递对准方案结构如图1所示。

图1 天文辅助的双惯组传递对准方案设计图

Fig.1 The scheme design of CNS-aided transfer alignment for double SIMU

该方案主要包括以下三个模块：

(1) 初始装订模块。 初始装订模块主要用于子INS的初始化。 在传递对准开始时刻， 子INS的姿态和位置采用主INS的姿态和位置直接进行“一次装订”粗对准， 因此， 子INS不需要专门的粗对准时间。

(2) 组合导航模块。 天文导航系统通过多矢量定姿方法和间接敏感地平定位方法可以提供高精度的姿态和位置信息。 将主INS和天文导航系统组合在一起， 以二者的姿态和位置信息差作为观测量， 利用滤波器估计和校正主INS的导航参数误差[5-8]， 使得主INS能长时间保持在较高精度。

(3) 传递对准模块。 以主INS输出的高精度导航信息为基准信息， 采用“姿态+速度”匹配算法， 将主、 子INS的速度和姿态误差作为观测量传送给卡尔曼滤波器， 最终修正子INS误差并对子INS器件误差进行标定。 保证在主、 子INS分离之后子INS的导航性能， 从而提高导弹命中率。

2 天文惯性组合导航模型建立

2.1 系统方程

在发射点惯性坐标系(li系)中建立主INS和天文导航的组合导航系统状态方程：

(1)

状态变量选为

(2)

F(t)为状态转移阵， 写作：

(3)

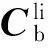
G(t)为噪声驱动阵：

(4)

系统噪声为

(5)

式中：ωgx,ωgy,ωgz为陀螺仪噪声；ωdx,ωdy,ωdz为加速度计噪声。

2.2 量测方程

(6)

姿态误差角与平台失准角并不等价， 二者之间的转换关系如下：

(7)

其中：θ和ψ代表弹道导弹实时的俯仰角和偏航角。 因此， 姿态误差量测方程可以写作：

Z1=H1X+v1

(8)

假设天文导航子系统的定位结果为rsc， 而主INS输出的定位结果是rsI。 位置误差观测量写作：

(9)

因此， 式(8)和式(9)建立起惯性/天文组合导航的量测方程：

(10)

综合状态方程(1)和量测方程(10)， 主INS与天文导航组合系统的数学模型得到建立。

3 弹载双惯组传递对准线性误差模型建立

3.1 弹体挠曲变形数学模型的建立

弹道导弹体积大， 结构细长， 应考虑挠曲变形。 挠曲变形角如图2(a)中θ所示。 而对于“姿态+速度”匹配算法， 还需要考虑安装误差角λ， 即主INS体坐标系和子INS体坐标系之间的夹角， 如图2(b)所示。

(11)

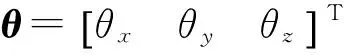
(12)

图2 主、 子INS间挠曲变形角和安装误差角

Fig.2 Flexure deformation angle and installation error angle between master INS and slave INS

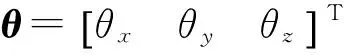
(13)

弹体的结构弹性系数βi与每个过程的相关时间τi有以下关系：

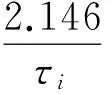
(14)

这样， 就完成了对弹体挠曲变形角的建模。

3.2 双惯组传递对准系统模型的建立

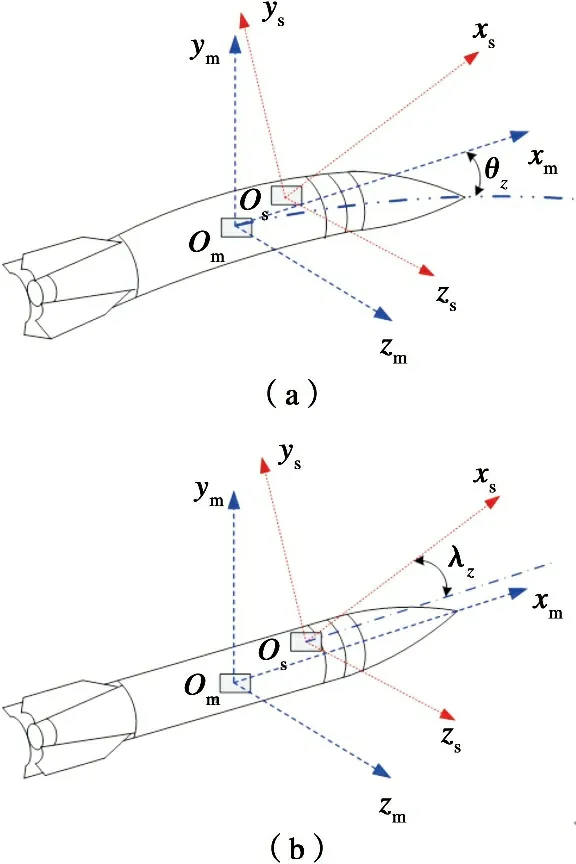
根据弹载双惯组传递对准方案， 传递对准系统方程的状态变量取为[10-11]

(15)

在发射点惯性坐标系(li系)中建立双惯组传递对准的系统状态方程为

(16)

式中：F(t)为状态转移矩阵；G(t)为噪声驱动阵；W(t)为系统噪声序列。

在“姿态+速度”匹配算法中， 系统的观测量是主、 子INS的速度误差以及姿态角误差：

(17)

观测方程可以写作：

Z(t)=H(t)X(t)+V(t)

(18)

式中：V(t)为量测噪声。

3.3 传递对准系统可观测度分析

由于惯性导航系统在传递对准过程中是一个线性时变的系统， 直接分析系统的可观测度具有很大难度。 目前， 基于奇异值分解的可观测度分析方法是最常用的方法， 该方法不仅可以分析出系统是否可观测， 还能具体分析某一个变量的可观测程度。 以弹道导弹的双惯组传递对准模型为研究对象， 利用基于奇异值分解的可观测性分析方法对系统模型中各个变量的可观测性与可观测程度进行分析[12-15]。 选取弹载双惯组传递对准开始时刻(即飞出大气层的时刻)作为可观测性分析的起始时间， 每间隔1 s观测一次， 一共观测100次， 每个状态量所对应奇异值的大小如图3所示。

图3 传递对准各状态量对应奇异值的直方图

Fig.3 Histogram of singular values for each state in transfer alignment

由图3可知， 在传递对准过程中， 可观测性矩阵的秩为21， 此时系统有21个状态或状态变量的组合是可观测的， 包括失准角φ、 速度误差δV、 安装误差角γ、 弹性变形角θ、 弹性变形角速度ωθ、 陀螺仪零位漂移KG0和加速度计一次项误差系数KA0。 其他的状态变量， 包括位置误差、 加速度计和陀螺仪的二次误差项都可认为不可观测。

3.4 双惯组传递对准降阶模型

卡尔曼滤波器虽然是处理线性系统的最优滤波器， 但滤波能力却受到系统阶数的限制。 因此， 适当减小滤波器的维数， 往往能够在不损失系统精度的情况下大大缩短收敛时间。 根据上述可观测度分析的结果， 保留位置误差， 可以将状态变量降阶为

(19)

降阶后的系统方程写作：

(20)

式中：F(t)为状态转移矩阵；G(t)为噪声驱动阵；W(t)为系统噪声序列。

(21)

系统噪声矩阵G(t)写作：

(22)

系统噪声序列为

W(t)=

(23)式中：wgx，wgy，wgz分别为陀螺仪三个方向的量测白噪声；wdx，wdy，wdz分别为加速度计三个轴向的量测白噪声；ηx，ηy，ηz为挠曲变形过程中的高斯白噪声。

系统量测模型中的速度误差匹配量写作：

(24)

式中：Vi(i=1, 2, 3)是速度观测的噪声。

假设主INS解算的姿态角为θm,γm,ψm， 而子INS计算得到的姿态角为θs,γs,ψs， 那么姿态误差匹配量可以写作：

(25)

(26)

式中：

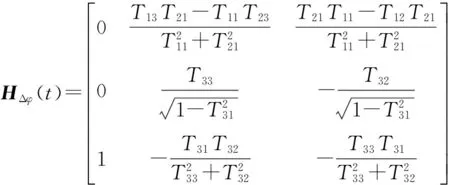
针对上述建立的“姿态+速度”误差匹配量， 可以建立传递对准系统的量测方程为

Z(t)=H(t)X(t)+V(t)

(27)

(28)

量测矩阵写作：

H(t)=

(29)

“姿态+速度”匹配的量测噪声序列为

(30)

综上所述， 式(20)和式(27)建立了双惯组传递对准的降阶模型。

4 仿真验证

4.1 仿真初始条件

(1) 导弹发射的初始位置及方位角

弹道导弹发射方位角为A=90°， 发射点地心纬度B=110°E， 发射点时角At=0°； 惯性器件采样间隔为T=0.1 s； 总仿真时间为Tall=1 000 s， 可以划分为以下几个阶段： 0～70 s是主、 子INS纯惯性导航时间， 70～880 s是双惯组传递对准时间， 880～1 000 s是子INS纯惯性导航阶段。

(2) 主、 子INS惯性器件误差参数

主INS惯性器件误差系数如表1所示。子INS惯性器件误差系数如表2所示。

表1主INS惯性器件误差系数

Table1InertiainstrumenterrorparametersofmasterINS

参数数值加速度计零位项误差KA0[5μg,5μg,5μg]T加速度计一次项误差KA1[1×10-6,1×10-6,1×10-6]T加速度计二次项误数KA2[1×10-6/g,1×10-6/g,1×10-6/g]T陀螺仪零位误差KG0[0.06(°)/h,0.06(°)/h,0.06(°)/h]T陀螺仪一次项误差系数KG1[1×10-6,1×10-6,1×10-6]T陀螺白噪声ωg[0.01(°)/h,0.01(°)/h,0.01(°)/h]T加速度计白噪声ωd[1μg,1μg,1μg]T初始失准角ϕmaster[30',50',30']T

表2子INS惯性器件误差系数

Table2InertiainstrumenterrorparametersofslaveINS

参数数值加速度计零位项误差KA0[100μg,100μg,100μg]T加速度计一次项误差KA1[1×10-5,1×10-5,1×10-5]T加速度计二次项误差KA2[1×10-5/g,1×10-5/g,1×10-5/g]T陀螺仪零位误差KG0[0.1(°)/h,0.1(°)/h,0.1(°)/h]T陀螺仪一次项误差系数KG1[1×10-8,1×10-8,1×10-8]T陀螺白噪声ωg[0.05(°)/h,0.05(°)/h,0.05(°)/h]T加速度计白噪声ωd[50μg,50μg,50μg]T初始失准角ϕmaster[10',10',60']T初始安装误差角λ[15',30',15']T马尔科夫相关时间μ[1″,3″,1″]T挠曲变形角方差σ[3',3',3']T

4.2 主INS组合导航结果

为分析天文导航和主INS的组合导航系统的性能， 验证天文导航对主INS的修正作用， 搭建了仿真平台， 针对主INS的纯惯性导航以及SINS/CNS组合导航进行100次蒙特卡罗仿真， 并分析仿真结果。 将二者的位置和姿态误差的统计结果进行对比， 如表3所示。

分析表3的数据可知， 在天文导航系统的辅助下， 主INS的定位结果相对于纯惯性定位结果， 精度大幅提高：SINS/CNS在X方向的位置误差是SINS的3.94%，Y和Z方向的定位误差仅为SINS的3%和2.65%。 三个轴向的姿态精度也得到了改善， 尤其是SINS的横滚角和航向角， 都减小到了5′以内。 可见， 天文导航系统提供的信息能有效减小主INS的导航误差， 实现高精度长时间导航。

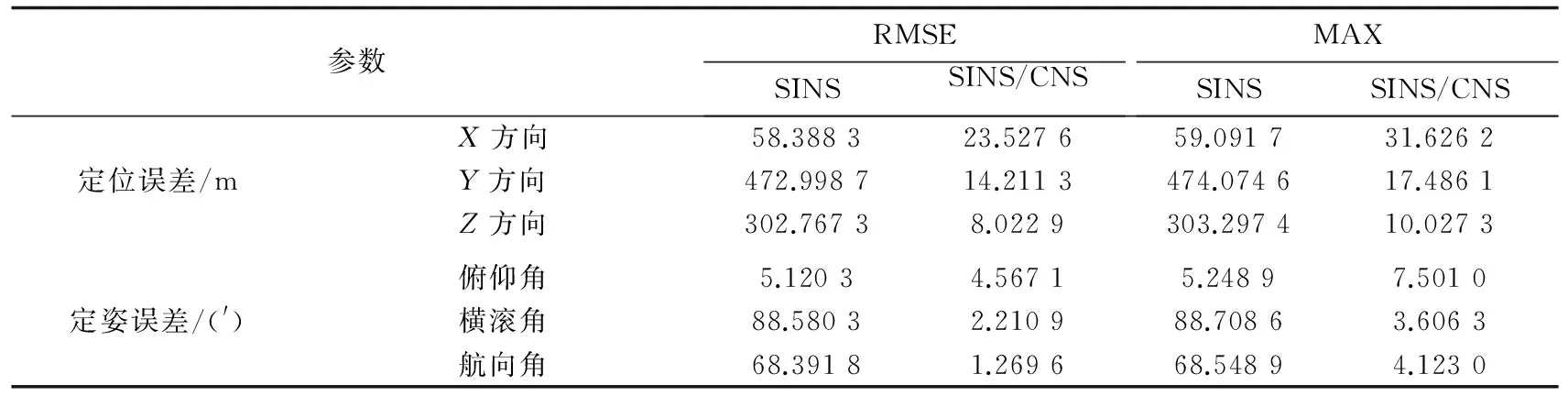
表3 SINS和SINS/CNS导航误差对比

4.3 子INS传递对准精度结果

在上述初始条件的基础上， 搭建仿真平台， 对弹载双惯组传递对准过程进行仿真试验， 结果如图4～9所示。

(1) 子INS绝对速度误差

传递对准阶段， 子INS的绝对速度误差如图4所示。 0～70 s子INS纯惯性导航阶段， 由于存在初始对准和惯性器件误差， 速度误差随时间而积累， 导航70 s时速度误差可达2 m/s， 如图4(a)所示； 在70～880 s内进行传递对准， 速度误差曲线如图4(b)所示。 仿真结果表明： 开始对准后， 在30 s内， 速度误差可以收敛到0.01 m/s以内， 速度快并且精度高。 完成传递对准后， 子INS在880～1 000 s内进行纯惯性导航， 由于对惯导器件误差等作了补偿， 速度误差的发散趋势较小， 如图4(a)所示。

(2) 位置和姿态误差

0～70 s子INS纯惯性导航阶段， 位置误差随时间而积累， 最大可达200 m， 70～880 s传递对准阶段， 如图5所示。 仿真结果表明， 开始对准后， 在30 s内， 位置误差收敛到10 m以内。 在主、 子INS分离之后， 由于对惯导器件误差等进行了补偿， 最终的位置误差不超过50 m， 可见导弹打击精度得到极大提高。

图4 子INS绝对速度误差

Fig.4 Absolute velocity error of slave INS

图6展示了全程子INS的姿态误差。 由于系统观测量包含姿态误差， 直接反映姿态的误差信息， 卡尔曼滤波利用这一信息可以很快估计出姿态的误差并进行校正。 仿真结果表明， 在20 s内， 姿态误差可以收敛到20″以内， 速度快且精度较高。

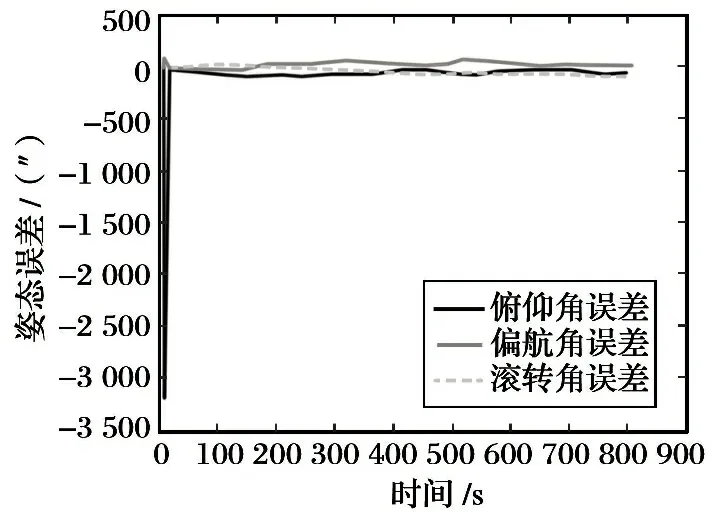
图5 子INS全程绝对位置误差

图6 子INS传递对准姿态角误差曲线

Fig.6 Attitude error curve of slave INS in transfer alignment stage

(3) 误差角估计结果

卡尔曼滤波不仅可以快速准确估计出姿态误差， 并且能够从中分离出挠曲变形角， 如图7所示。 仿真结果表明：X与Y方向的弹体弹性变形能够达到较好的跟踪效果， 且变形角跟踪稳定时基本能够保持在10″的精度范围内。 但是Z方向的效果并不理想， 这是因为弹道导弹的发射角是90°， 在Z方向上没有任何机动， 该方向可观测度较低的缘故。

从估计的误差角中减去挠曲变形角， 就可得到安装误差角， 如图8所示。 安装误差角的估计精度在5″以内。

(4) 子INS器件标定结果

传递对准对子INS陀螺仪常值漂移的标定结果如图9所示。 可以看出： 三个方向陀螺仪的估计精度都较高， 且估计速度较快， 400 s就可以收敛到理论值附近。 由于数学平台失准角的变化率直接反映了陀螺的零位漂移， 因而， 引入姿态基准的传递对准匹配方式能够增强陀螺零位漂移的可观测度， 从而加快陀螺零位漂移的标定速度和精度。

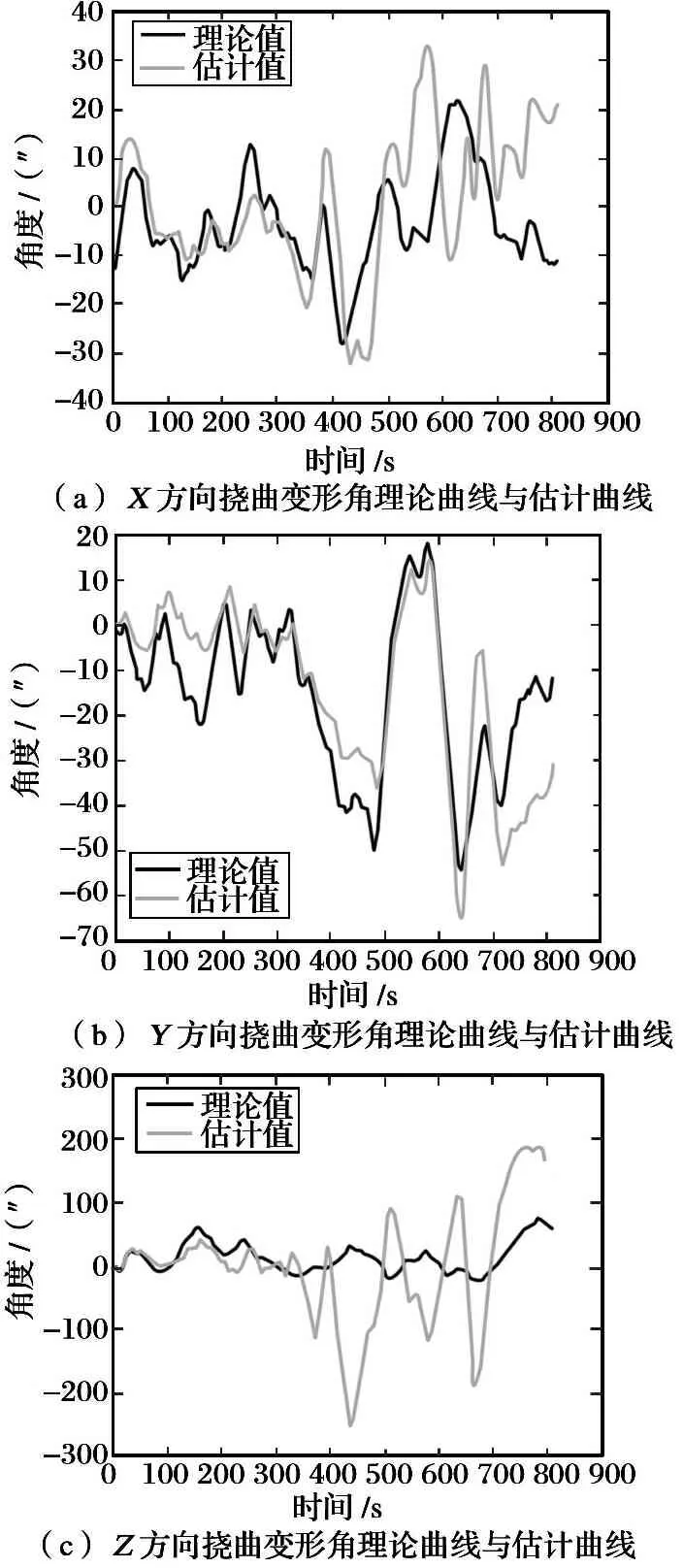
图7 挠曲变形角估计结果

图8 安装误差角估计结果

图9 子INS陀螺仪常值漂移估计曲线
Fig.9 Estimation results of gyroscope constant drifts of slave INS

加速度计零偏的估计曲线如图10所示， 在70～880 s的传递对准过程中， 三个轴向的零位偏置在100 s内快速收敛到理论值附近。 加速度计零位偏置是造成速度解算误差的一个主要因素， 所以从速度误差的量测中能够很好地分离出加速度计零位偏差。

图10 子INS加速度计零偏估计结果

Fig.10 Estimation results of accelerometer zero bias of slave INS

5 结 束 语

本文设计了一种基于天文辅助的弹载双惯组空中传递对准方案， 不仅能长时间保证主INS精度， 还可以有效改善子INS的对准精度。 为解决系统模型阶次过高， 对准精度和快速性受影响的问题， 对传统传递对准数学模型进行了可观测度分析， 得到相应的降阶模型。 仿真结果表明， 传递对准速度快且精度高， 不仅可以成功估计出挠曲变形角， 子INS的姿态基准、 位置误差和速度误差也都可以得到精确的修正， 同时对准过程也实现了对子INS惯性器件主要误差项的标定。 所设计的双惯组传递对准方案是合理且可行的。

[1] 乔道鹏. 机载导弹的传递对准研究[D]. 哈尔滨： 哈尔滨工业大学, 2008. Qiao Daopeng．Research on Transfer Alignment of the Missile Onboard the Aircraft[D]．Harbin： Harbin Institute of Technology， 2008．(in Chinese)

[2] 丁国强. 惯性导航系统传递对准技术关键问题研究[D]. 哈尔滨： 哈尔滨工程大学, 2010. Ding Guoqiang．To Research on the Transfer Alignment Problems of Inertial Navigation Systems[D]．Harbin： Harbin Engineering University， 2010．(in Chinese)

[3] 张勤拓. 机载导弹SINS动基座传递对准技术研究[D]. 哈尔滨： 哈尔滨工程大学, 2010. Zhang Qintuo． Transfer Alignment of SINS for Airborne Missiles[D]． Harbin： Harbin Engineering University， 2010．(in Chinese)

[4] 王新龙, 申亮亮, 马闪. 摇摆基座SINS快速精确传递对准方法[J]. 北京航空航天大学学报, 2009, 35(6): 728-731. Wang Xinlong， Shen Liangliang， Ma Shan． Transfer Alignment of Strapdown Inertial Navigation Systems on Rolling Bases[J]．Journal of Beijing University of Aeronautics and Astronautics， 2009， 35(6)： 728-731．(in Chinese)

[5] Yang Shujie, Yang Gongliu, Zhu Zhanlong, et al. Stellar Refraction-Based SINS/CNS Integrated Navigation System for Aerospace Vehicles[J]. Journal of Aerospace Engineering, 2016, 29(2): 04015051.

[6] Wang Xinlong, Ma Shan. A Celestial Analytic Positioning Method by Stellar Horizon Atmospheric Refraction[J]. Chinese Journal of Aeronautics, 2009, 22(3): 293-300.

[7] 王鑫, 王新龙. 弹道导弹SINS/CNS组合导航系统建模与性能仿真[J]. 航空兵器, 2015(2): 21-25. Wang Xin，Wang Xinlong．System Modeling and Perfor-mance Simulation on SINS/CNS Integrated Navigation System for Ballistic Missile[J]．Aero Weaponry， 2015(2)： 21-25．(in Chinese)

[8] 陈霞. 天文/惯性组合导航模式研究[J]. 光学与光电技术, 2003, 1(3): 21-25. Chen Xia．Investigation on Celestial/Inertial Integrated Navigation Patterns[J]．Optics & Optoelectronic Technology， 2003， 1(3)： 21-25． (in Chinese)

[9] 王新龙. 捷联式惯导系统动、 静基座初始对准[M]. 西安： 西北工业大学出版社, 2013. Wang Xinlong．Initial Alignment of Strap-Down Inertial Navigation System on Moving or Stationary Base[M]．Xi’an： Northwestern Polytechnical University Press， 2013．(in Chinese)

[10] 林敏敏, 房建成, 高国江. 一种有效的空-空导弹捷联惯导系统快速精确传递对准方法[J]. 中国惯性技术学报, 2001， 9(3): 24-28， 47. Lin Minmin，Fang Jiancheng，Gao Guojiang．An Efficient Method of Fast and Accurate Transfer Alignment of SINS Used on Air-to-Air Missiles[J]．Journal of Chinese Inertial Technology， 2001， 9(3)： 24-28， 47．(in Chinese)

[11] 郑辛, 武少伟, 吴亮华. 导弹武器惯导系统传递对准技术综述[J]. 导航定位与授时, 2016, 3(1)： 1-8. Zheng Xin，Wu Shaowei，Wu Lianghua．Overview of Transfer Alignment Technology of Missile Inertial Navigation System[J]．Navigation Positioning and Timing， 2016， 3(1)： 1-8．(in Chinese)

[12] 董海波. 基于可观测性分析的SINS传递对准优化方法研究[D]. 哈尔滨： 哈尔滨工程大学， 2015. Dong Haibo．Optimization Method Research of SINS Transfer Alignment Based on Observability Analysis[D]．Harbin：Harbin Engineering University，2015．(in Chinese)

[13] Liu Baiqi, Fang Jiancheng. A New Adaptive Feedback Kalman Filter Based on Observability Analysis for SINS/GPS[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 430-436.

[14] 戴邵武, 丛培胜, 丛源材. 基于“速度+姿态”快速传递对准的可观测性分析[J]. 海军航空工程学院学报, 2009, 24(2): 167-170. Dai Shaowu，Cong Peisheng，Cong Yuancai．Analysis of Observability for Transfer Alignment Based on “Velocity+Attitude”[J]．Journal of Naval Aeronautical and Astronautical University， 2009， 24(2)：167-170．(in Chinese)

[15] 吴海仙, 俞文伯, 房建成. SINS/CNS组合导航系统的降阶模型研究[J]. 航天控制, 2005, 23(6): 12-16. Wu Haixian，Yu Wenbo，Fang Jiancheng．Research on Reduced Dimension Model of SINS/CNS Integrated Navigation System[J]．Aerospace Control， 2005， 23(6)： 12-16．(in Chinese)

CNS-AidedTransferAlignmentSchemeforMissile-BorneDoubleSIMU

ZhuJiafang1,WangXinlong1,LiQunsheng2,WangDun3

(1.SchoolofAstronautics，BeihangUniversity,Beijing100191,China;2.SchoolofInstrumentationScienceandOpto-ElectronicsEngineering,BeihangUniversity,Beijing100191,China； 3.StateKeyLaboratoryofSpace-GroundInformationTechnology,Beijing100191,China)

A CNS-aided transfer alignment scheme for missile-borne double SIMU is proposed. For the ballistic missile flies above the atmosphere most of the time, CNS is introduced to assist master INS, so that master INS can maintain high accuracy for a long time. Taking the flexure deformation into consideration, a high precise transfer alignment mathematic model for double SIMU is established. According to the observability degree analysis results of each state in the model, a reduced-dimension model is got. Based on the proposed transfer alignment model, "attitude+velocity" matching method is employed to estimate and compensate the errors of slave INS navigation parameters and inertial equipments. Simulation results demonstrate that, the proposed transfer alignment scheme can not only guarantee the high accuracy of master INS, but also improve the alignment precision of slave INS.

celestial navigation; transfer alignment; double SIMU; observability analysis

10.19297/j.cnki.41-1228/tj.2017.04.007

2016-11-21

航空科学基金项目(20130151004； 2015ZC51038)； 天地一体化信息技术国家重点实验室开放基金项目(2015-SGIIT-KFJJ-DH-01)

祝佳芳(1990-)， 女， 四川乐山人， 硕士研究生， 研究方向为惯性导航、 组合导航。

祝佳芳， 王新龙， 李群生， 等. 基于天文辅助的弹载双惯组空中传递对准方案[ J]. 航空兵器， 2017 ( 4 ): 40-48. Zhu Jiafang, Wang Xinlong, Li Qunsheng, et al. CNS-Aided Transfer Alignment Scheme for Missile-Borne Double SIMU[ J]. Aero Weaponry, 2017( 4): 40-48. ( in Chinese)

TJ765.1; V249.32+3

： A

： 1673-5048(2017)04-0040-09