一种光纤陀螺随机振动误差高精度建模方法
2017-09-15柴嘉薪王新龙李群生
柴嘉薪, 王新龙, 王 盾, 李群生
(1. 北京航空航天大学 宇航学院, 北京 100191; 2. 天地一体化信息技术国家重点实验室, 北京 100086; 3. 北京航空航天大学 仪器科学与光电工程学院, 北京 100191)
一种光纤陀螺随机振动误差高精度建模方法
柴嘉薪1, 王新龙1, 王 盾2, 李群生3
(1. 北京航空航天大学 宇航学院, 北京 100191; 2. 天地一体化信息技术国家重点实验室, 北京 100086; 3. 北京航空航天大学 仪器科学与光电工程学院, 北京 100191)
工程应用中, 随机振动对光纤陀螺的测量精度有着重要影响。 本文通过对光纤陀螺振动数据的特性分析, 提出了一种经验模态分解法、 时间序列建模方法以及Kalman滤波算法相结合的光纤陀螺随机振动误差高精度建模方法, 实现了对光纤陀螺振动误差的高精度拟合, 该方法可应用于工程环境中对光纤陀螺随机振动误差的高精度补偿。
光纤陀螺; 随机振动; 误差; 经验模态分解; AR模型; Kalman滤波
0 引 言
光纤陀螺在实际工程应用中, 冲击、 振动引起的光纤环的应力变化、 器件尾纤振动以及结构的共振都将引起陀螺误差[1], 表现为陀螺零位发生偏移, 严重影响光纤陀螺在实际工作中的精度和稳定性。 目前, 工程中解决光纤陀螺敏感振动环境主要采用以下两种技术途径:一是在光纤陀螺的设计和生产阶段采取改善封装结构、 控制胶粘剂涂覆用量、 引入橡胶减振装置[1]等物理方法, 在一定程度上减小振动引起的误差, 提高器件固有精度, 但工艺水平提升空间有限, 效果仍无法满足精度需求较高的捷联系统; 二是在光纤陀螺精度确定的前提下, 分析振动数据特性, 并由软件实现对振动误差的准确建模、 滤波及补偿。 第二种方法因其低成本、 应用广的优势, 成为提高光纤陀螺精度的重要手段。
常用的数据分析、 建模方法包括小波分析、 神经网络建模和时间序列建模等。 基于小波分析的趋势项提取方法[2-4], 过程繁杂, 且自身存在的限制通常情况下会造成虚假的谐波, 依此进行的一系列分析也将失去原有的物理意义; 神经网络建模方法得到的近似补偿模型包含了所有的非线性影响因素, 但数据随机性较大时, 建模精度很低, 不适用于处理光纤陀螺随机振动数据; 时间序列建模方法[5-6]是利用有限样本数据拟合成具有一定精度的时间序列模型, 具有使用方便、 可操作性好的优点, 因此应用比较广泛。
针对以上问题, 本文研究了一种对高精度光纤陀螺在随机振动影响下产生的有色噪声建立误差模型进行拟合的方法, 解决了传统建模预处理方法无法直接提取光纤陀螺振动数据非随机项的问题, 提高了对光纤陀螺随机振动误差的拟合精度, 并利用某型号光纤捷联惯组(内含三只某型号高精度光纤陀螺仪)的实测数据, 验证了该建模方法的有效性。
1 FOG随机振动数据及特性分析
由光纤捷联惯组的随机振动试验采集得到的X,Y,Z向陀螺通道输出的转动角增量脉冲数, 依据已知的陀螺通道测量模型及极性规定得到相应轴向的转动角速度, 其中X轴振动试验的振动数据时序分布如图1所示。

图1X轴振动试验的振动数据
Fig.1 Vibration data ofXaxis vibration experiment
以X轴振动试验中陀螺X轴通道为例进行分析, 其输出序列y(n)振动段(1 320~1 495 s)数据的时域、 频域分布如图2所示。 其中, 横坐标t表示每秒单位时间内包含2 000组采集数据, 即t=n/2 000。

图2y(n)时域、 频域分布图
Fig.2 Distribution of time domain and frequency domain
由图2可见, 随机振动数据y(n)的振动噪声比较明显, 且频谱图上的非随机项都淹没在低频噪声的频谱之中, 并不凸显。 传统的提取非随机项方法是通过对数据y(n)时域、 频域图的观察, 直观判断明显的非随机项, 再通过经验试凑确定非随机项的拟合函数。 因此, 传统的提取非随机项方法对光纤陀螺的随机振动数据不再适用, 需要选用其他有效的数据分离方法提取非随机项, 再进行时间序列建模和数据拟合。
2 一种光纤陀螺振动误差建模方法
在振动试验中, 将随机振动看作一个随机的角速率输入, 以处理随机噪声的方式处理光纤陀螺仪的振动数据。 由于系统工作条件的变化, 往往会造成从实际系统中获得的观测序列的非平稳性[7]。 通常, 可以将试验得到的数据y(n)分解为
y(n)=u(n)+s(n)+x(n)
(1)
式中:u(n)为趋势项;s(n)为周期项, 与u(n)统称为非随机项;x(n)由随机因素引起, 一般可假设为平稳时间序列。 由此可见, 获得试验数据y(n)后需先进行非随机项提取。
针对随机振动数据, 将经验模态分解法、 时间序列建模方法以及Kalman滤波算法进行有机结合, 设计了一种光纤陀螺随机振动误差高精度建模方法, 如图3所示。

图3 光纤陀螺高精度误差建模方法设计图
Fig.3 Design of high precision error modeling method for fiber optic gyroscope
本建模方法主要分为提取非随机项、 时间序列建模以及数据拟合三个部分:
(1) 提取非随机项: 对经过预处理的振动数据进行特性分析, 针对非随机项难以直接提取的数据特性, 采用由数据驱动的、 自适应性较强的经验模态分解法提取振动数据y(n)中的非随机项u(n)+s(n), 并得到N个固有模态函数(IMF), 各IMFs分量之和即为平稳序列x(n)。
(2) 时间序列建模: 对满足平稳性和非白噪声性的各IMFs分量建立满足适应性要求的时间序列模型。

3 振动试验数据处理方法
3.1 经验模态分解法


(2)
3.2 时间序列建模方法
3.2.1 模型识别

表1ARMA(p,q)模型特点
Table1CharacteristicsofARMA(p,q)model

模型名称AR(p)MA(q)ARMA(p,q)ACF拖尾q步截尾拖尾PACFp步截尾拖尾拖尾
3.2.2 模型定阶与参数估计
模型定阶与参数估计即确定模型参数的个数及估计值。 模型识别可初步判定AR或MA模型的阶数, 为实现高精度建模, 还需结合最佳准则函数定阶法[12]以确定模型的准确阶数。 这里选用考评综合最优配置的AIC准则与BIC准则对模型阶数进行判断。
AIC准则是将模型拟合效果与模型参数数量这两个目标进行适当的综合。 BIC准则相比于AIC准则对模型参数考虑得更多。 当样本个数趋于无穷时, 由BIC准则确定的最佳模型阶数往往比AIC准则确定的低, 且更准确。
在确定了模型阶数的基础上, 进行参数的估计值计算。 常用的参数估计方法有矩估计法[13]、 最小二乘估计法和极大似然估计法等。 与最小二乘估计法和极大似然估计法相比, 矩估计法计算量相对较小, 估计精度较低。 其基本思想是ARMA模型的自相关函数(矩函数)可以表示为未知的模型参数的函数, 反过来, 模型参数原则上也可由自相关函数(矩函数)来表示。 这样, 用计算出的样本自相关函数代替理论自相关函数, 就可以得到参数的估计值。 因此, 选用矩估计法进行模型的参数估计。
3.2.3 模型适应性检验
模型的适应性检验实质上就是检验{an}序列是否为白噪声序列。 一个时间序列的适合模型应该完全或基本上解释了系统的动态性(即数据序列的相关性), 从而模型中残差序列{an}应该是白噪声序列。
残差序列{an}可由估计出来的ARMA模型计算得到:
(3)
通常采用逆推方法得到残差序列{an}:
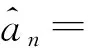
(4)
得到残差序列{an}后, 再利用自相关系数准则[12]对模型进行适应性检验。
3.3 基于AR模型的Kalman滤波拟合方法
Kalman滤波与式(3)所示的建模结果结合使用时, 需将AR模型转化为离散系统状态空间模型:
(5)

4 振动误差建模方案验证与分析
4.1 提取非随机项
以X轴振动试验采集得到的陀螺X轴通道输出序列y(n)的振动段(1 320~1 495 s)序列为例, 对上述振动误差建模方案进行正确性验证。y(n)经过经验模态分解为18个固有模态函数以及非随机项r, 部分结果如图4所示(由于篇幅所限, 这里省略了IMF9~IMF17)。

图4X轴振动试验IMF1~IMF8, IMF18和r
Fig.4 IMF1~IMF8, IMF18 androfXaxis vibration test
时间序列建模要求时间序列是满足平稳性的非白噪声序列, 因此, 需对EMD结果中各IMFs的平稳性及白噪声性进行检验。

然后, 进行白噪声性检验:利用自相关系数准则检验各IMFs的白噪声性, 结果表明各IMFs序列均非白噪声。
4.2 时间序列建模
对平稳时间序列IMF1进行模型识别、 模型定阶, 如图5~6所示。 由图5可知, ACF函数呈拖尾状, PACF函数呈截尾状, 依据表1判断AR(p)模型为IMF1的适用模型。 由图6可知, AIC和BIC准则判断出的最佳模型阶数均为7。 在此基础上, 进行模型参数估计和模型适用性检验, 以得到最佳拟合模型。 同理, 完成对各IMFs的时间序列建模, 部分结果如表2所示。
4.3 数据拟合
采用基于AR模型的Kalman滤波拟合方法实现对各IMFs序列的拟合,P的初值选为单位阵,X的初始值选为实际采集数据的前p个数据项。 完成各IMFs建模后, 将各AR(p)的拟合结果叠加, 再加上EMD提取所得的非随机项的补偿, 即对X轴振动试验中陀螺X轴通道输出序列y(n)振动段的拟合结果, 见图7。
从图7中可以看到, 基于AR模型的Kalman滤波拟合方法可以实现对随机振动环境下陀螺输出噪声的高精度拟合, 其拟合曲线相较于单独使用AR模型拟合的曲线更贴近原始序列。
总体概率分布曲线见图8。 三种概率分布曲线变化趋势基本吻合, 但峰值1 895>1 836>1 807, 基于AR模型的Kalman滤波拟合序列的分布相比于单纯AR模型拟合序列更接近原始序列, 二者的拟合误差见图9。

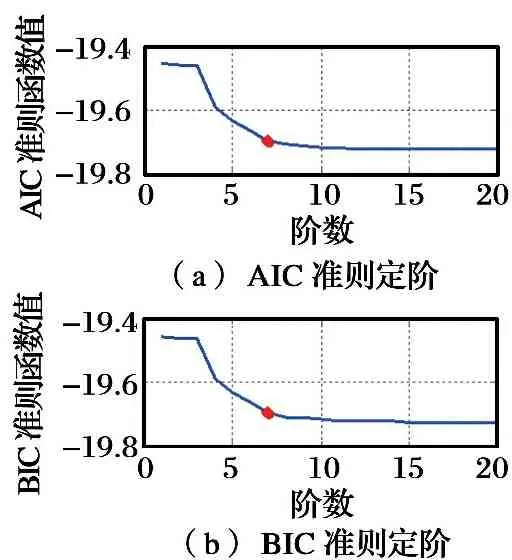
图5 IMF1模型识别

图6 IMF1模型定阶

图7 AR模型拟合和基于AR模型的Kalman滤波拟合序列结果图
Fig.7 Sequence fitting results of AR model and Kalman filter based on AR model


图8 总体概率分布曲线图
图9 AR模型拟合和基于AR模型的Kalman滤波拟合序列误差图
Fig. 9 Sequence fitting errors of AR model and Kalman filter based on AR model
Kalman滤波前后拟合误差的统计特性如表3所示。 基于AR模型的Kalman滤波拟合误差的幅值、 均值和标准差均明显小于AR模型拟合误差。
表3Kalman滤波前后拟合误差比较
Table3ComparisonoffittingerrorsbeforeandafterKalmanfiltering

Kalman滤波前Kalman滤波后误差均值/((°)/s)7.3677×10-63.9332×10-6误差标准差/((°)/s)0.00410.0018
因此, 使用本文提出的基于AR模型的Kalman滤波拟合方法对振动误差的拟合结果对陀螺输出的随机振动误差进行补偿后, 大大减小随机振动对光纤陀螺测量精度的影响。
5 结 论
针对工程应用中随机振动的影响会降低光纤陀螺测量精度的问题, 提出了一种经验模态分解法、 时间序列建模方法以及Kalman滤波算法相结合的光纤陀螺随机振动误差高精度建模方法。 通过经验模态分解法对振动数据提取非随机项, 再对平稳序列进行时间序列建模, 最后基于AR模型的Kalman滤波拟合方法实现了对光纤陀螺振动误差的高精度拟合。 解决了传统预处理方法无法直接提取光纤陀螺振动数据非随机项的问题, 减小了单纯时间序列建模方法对光纤陀螺振动误差拟合的方差与标准差, 提高了拟合精度。 此方法可用于工程中对光纤陀螺随机振动误差的高精度补偿。
[1] 吴磊, 孙枫, 程建华, 等. 光纤陀螺捷联系统振动误差补偿研究[J]. 传感器与微系统, 2009, 28(6): 43-45. Wu Lei, Sun Feng, Cheng Jianhua, et al. Research on Vibration Error Compensation of FOG SINS[J]. Transducer and Microsystem Technologies, 2009, 28(6): 43-45. (in Chinese)
[2] 王庆贺. 基于小波去噪与DRNN的光纤陀螺随机误差建模研究[J]. 航空兵器, 2015(4): 16-20. Wang Qinghe. Research of Gyro Random Error Modeling Based on the Wavelet and DRNN[J]. Aero Weaponry, 2015(4): 16-20.(in Chinese)
[3] 刘伟宁. 基于小波域扩散滤波的弱小目标检测[J]. 中国光学, 2011, 4(5): 503-508. Liu Weining. Dim Target Detection Based on Wavelet Field Diffusion Filter[J]. Chinese Optics, 2011, 4(5):503-508.(in Chinese)
[4] 刘希佳, 陈宇, 王文生, 等. 小目标识别的小波阈值去噪方法[J]. 中国光学, 2012, 5(3): 248-256. Liu Xijia, Chen Yu, Wang Wensheng, et al. De-Noising Algorithm of Wavelet Threshold for Small Target Detection[J]. Chinese Optics, 2012, 5(3): 248-256.(in Chinese)
[5] 冀振元. 时间序列分析与现代谱估计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2016. Ji Zhenyuan. Time Series Analysis and Modern Spectral Estimation[M]. Harbin: Harbin Engineering University Press, 2016.(in Chinese)
[6] 王新龙, 杜宇, 丁杨斌. 光纤陀螺随机误差模型分析[J]. 北京航空航天大学学报, 2006, 32(7): 769-772. Wang Xinlong, Du Yu, Ding Yangbin. Investigation of Random Error Model for Fiber Optic Gyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(7): 769-772.(in Chinese)
[7] 严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2012. Yan Gongmin, Li Sihai, Qin Yongyuan. Measurement and Data Analysis of Inertial Instrument[M]. Beijing: National Defence Industry Press, 2012.(in Chinese)
[8] Huang N E, Shen Z, Long S R. A New View of Nonlinear Water Waves: The Hilbert Spectrum[J]. Annual Review of Fluid Mechanics, 2003, 31(1): 417-457.
[9] 米剑, 张春熹, 李铮, 等. 偏光干涉对光纤陀螺性能的影响[J]. 光学学报, 2006, 26(8): 1140-1144. Mi Jian, Zhang Chunxi, Li Zheng, et al. Effect of Polarization Interference on Fiber Optic Gyro Performance[J]. Acta Optica Sinica, 2006, 26(8): 1140-1144.(in Chinese)
[10] 李新忠, 岱钦, 王希军, 等. 多尺度小波降噪的数字散斑相关搜索[J]. 光学精密工程, 2007, 15(1): 57-62. Li Xinzhong, Dai Qin, Wang Xijun, et al. Digital Speckle Correlation Method of Multi-Scale Wavelet Noise Reduction[J]. Optics and Precision Engineering, 2007, 15(1): 57-62.(in Chinese)
[11] 赵雪花, 安莉莉, 袁旭琦. 基于HHT和R/S分析的黄河上游年径流序列演变模式分析[J]. 水电能源科学, 2013(7): 9-12. Zhao Xuehua, An Lili, Yuan Xuqi. Analysis of Annual Runoff Series Evolution Model in the Upper Reaches of the Yellow River Based on HHT and R/S[J]. Water Resources and Power, 2013(7): 9-12.(in Chinese)
[12] 杨叔子, 吴雅, 轩建平. 时间序列分析的工程应用[M]. 武汉: 华中科技大学出版社, 2007. Yang Shuzi, Wu Ya, Xuan Jianping. Engineering Application of Time Series Analysis[M]. Wuhan:Huazhong University of Technology Press, 2007.(in Chinese)
[13] 王新龙, 陈涛, 杜宇. 基于ARMA模型的光纤陀螺漂移数据建模方法研究[J]. 弹箭与制导学报, 2006, 26(1): 5-7. Wang Xinlong, Chen Tao, Du Yu.The Drift Method of Fiber Optic Gyros Based on the ARMA Model[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(1): 5-7.(in Chinese)
AHighPrecisionModelingMethodforRandomVibrationErrorofFiberOpticGyroscope
ChaiJiaxin1,WangXinlong1,WangDun2,LiQunsheng3
(1.SchoolofAstronautics,BeihangUniversity,Beijing100191,China;2.StateKeyLaboratoryofSpace-GroundInformationTechnology,Beijing100086,China; 3.SchoolofInstrumentationScienceandOpto-ElectronicsEngineering,BeihangUniversity,Beijing100191,China)
In engineering applications, the random vibration has important influence on the measurement accuracy of fiber optic gyroscope. Based on analyzing the vibration data characteristics of fiber optic gyroscope, a high precision modeling method for random vibration error of fiber optic gyroscope is proposed, which combines empirical mode decomposition method, time series modeling method and Kalman filtering algorithm.The proposed modeling method can realize high precision fitting to vibration error of fiber optic gyroscope. This method can be applied to the high precision compensation for random vibration error of fiber optic gyroscope in engineering environment.
fiber optic gyroscope; random vibration; error; EMD; AR model; Kalman filtering
10.19297/j.cnki.41-1228/tj.2017.04.008
2016-11-25
国家自然科学基金项目(61673040); 航空科学基金项目(2015ZC51038); 天地一体化信息技术国家重点实验室开放基金项目(2015-SGIIT-KFJJ-DH-01); 2015年度北京航空航天大学教改资助项目
柴嘉薪(1993-), 女, 河北石家庄人, 硕士研究生, 研究方向是惯性导航、 组合导航。
柴嘉薪, 王新龙, 王盾, 等. 一种光纤陀螺随机振动误差高精度建模方法[ J]. 航空兵器, 2017( 4): 49-54. Chai Jiaxin, Wang Xinlong, Wang Dun, et al. A High Precision Modeling Method for Random Vibration Error of Fiber Optic Gyroscope[ J]. Aero Weaponry, 2017( 4): 49-54.( in Chinese)
TJ765; V241.5
: A
: 1673-5048(2017)04-0049-06
