星形人字齿轮传动系统振动模式的理论研究

郝立峰 王三民 王飞鸣

1.西北工业大学机电学院，西安,7100722.中国航空工业集团公司沈阳发动机设计研究所，沈阳，110015

星形人字齿轮传动系统振动模式的理论研究

郝立峰 王三民 王飞鸣

1.西北工业大学机电学院，西安,7100722.中国航空工业集团公司沈阳发动机设计研究所，沈阳，110015

采用集中质量法建立了含N个星轮的星形人字齿轮传动系统的弯-扭-轴耦合动力学模型和动力学方程。模型中将人字齿轮看作由两斜齿轮通过无质量弹簧连接而成。求解了系统的固有圆频率和固有振型，根据振动模式将星形人字齿轮传动系统的固有振动模式进行分类，并对其重根数和固有频数个数进行了理论研究。结果表明：星形人字齿轮传动系统含有4种典型振动模式，即：中心构件轴向-扭转耦合模态(重根数r=1)，星轮模态(重根数r=N-3，N>3)，中心构件平动模态(重根数r=2)，星轮与中心轮耦合模态(重根数r=2)。

星形人字齿轮;传动系统；耦合模态；星轮模态；平动模态

0 引言

星形齿轮传动在航空领域得到广泛应用[1]。星形传动系统中的噪声和振动问题一直是齿轮传动领域研究的重点。国外学者LIN等[2]分析了单节点三自由度的直齿行星齿轮系统固有特性,将其模态分成三类并进行了证明；KIRACOFE等[3]将直齿行星齿轮传动的理论分析模型扩展到了多级行星传动；PARKER[4]提出通过调整啮合相位差来抑制系统的三种振动模式；基于对直齿行星传动振动模式的分类，LIN等[5-6]对直齿行星传动系统的模态灵敏度进行了分析，得出了系统模态对于系统参数灵敏度的解析表达式，并在此基础上分析了直齿行星传动模态跃迁的相关规律，为系统参数选择提供了指导。国内学者林何等[7]对斜齿行星传动系统模态进行分类并研究了它的非线性特性；卜忠红[8]研究了人字齿行星传动系统固有特性，并对其模态进行了分类和证明；任菲等[9]研究了太阳轮浮动对行星人字齿轮传动的动态特性的影响。

本文建立了星形人字齿轮系统弯-扭-轴耦合动力学模型，将人字齿轮等效为由退刀槽相连的左右两斜齿，研究系统固有特性，将系统模态进行分类，证明了人字齿轮传动4种典型模态，前3种模态与LIN等[2]对直齿行星传动系统分类得出的3种模态类似，第4种星轮与中心轮耦合模态为人字齿特有的新型模态，此研究为单级和多级星形人字齿轮振动抑制及相位调谐机理的研究打下了理论基础。

1 动力学模型及方程的建立

人字齿星形传动减速器弯-扭-轴耦合动力学模型如图1所示,它由太阳轮s、内齿圈r及N(N为星轮个数)个星轮p组成(图1中量符号下标ξ=c,s,r)。其中，太阳轮和内齿圈分别作为输入、输出构件，星轮通过星形架与机架固连；内齿圈为组合式，采用两个旋向相反的斜齿轮拼接而成，太阳轮和各星形轮为整体式。图1中β为人字齿轮基圆螺旋角；ksp、krp分别为太阳轮星轮和星轮内齿圈单边斜齿啮合刚度。在动力学模型中，将单个人字齿轮分为左右斜齿两部分，每一部分考虑x、y、z、θz四个自由度，系统共有8N+20个自由度；各星轮沿周向均匀分布，且质量、支撑刚度等参数均相同；人字齿轮左右侧完全对称。下文中量符号的下标s、pn、c、r分别代表太阳轮、星轮、星形架、内齿圈的相关参量，下标L、R表示人字齿轮的左右侧两部分相关参量。

图1 星形人字齿轮传动动力学模型Fig.1 Dynamical model of double-helical star geartransmission

模型构件较多，采用有限元思想建立动力学模型[10]。图2表示第n个星轮与太阳轮啮合，其中第n个星轮的安装角φn=2π(n-1)/N；齿轮副的啮合线平面与中心构件y轴夹角为ψspn,且有

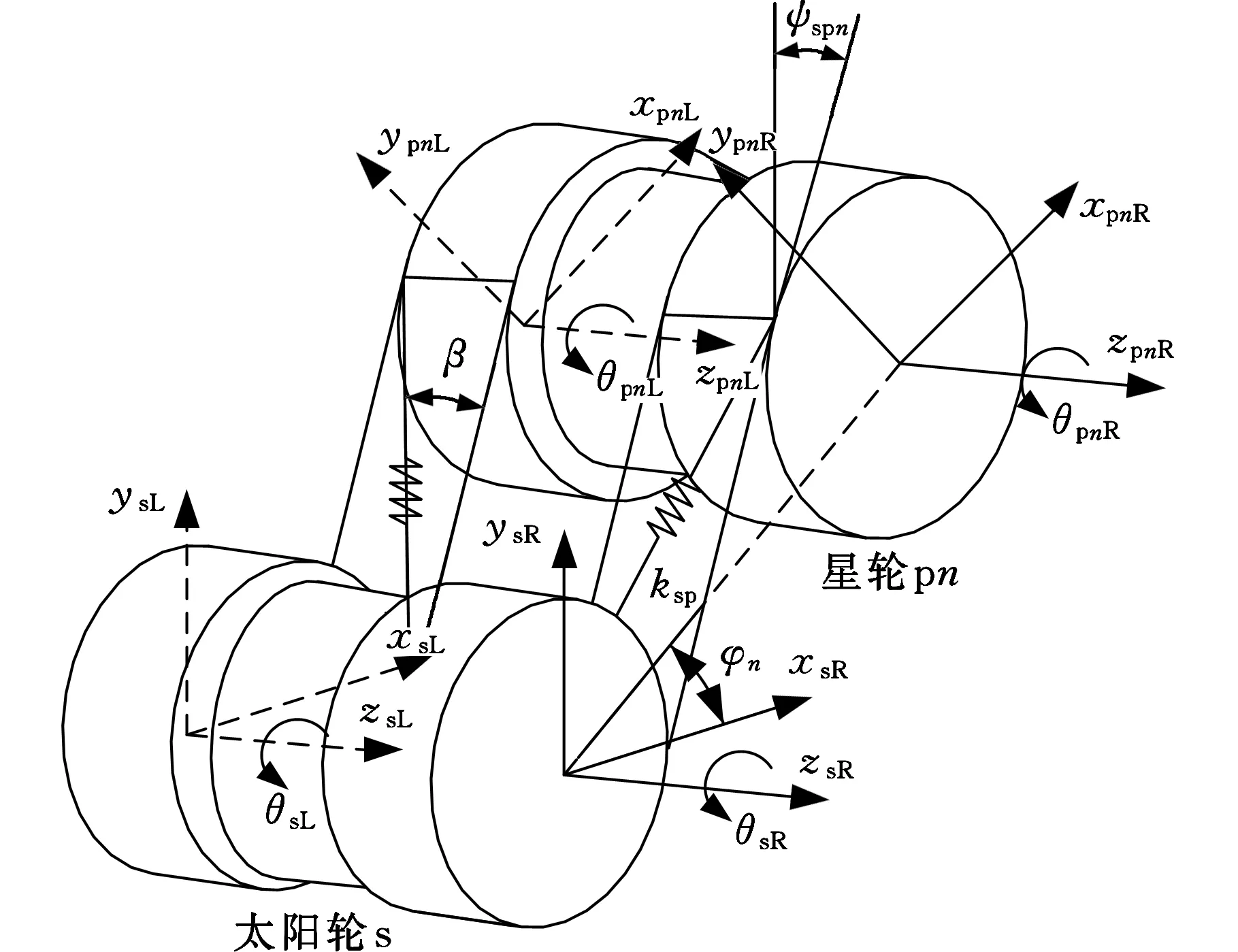
图2 太阳轮-星轮n齿轮副动力学模型Fig.2 Dynamic model of sun-starn pair

(1)

式中，α为系统人字齿轮端面压力角。

以太阳轮星轮右侧单边啮合为例，导出单边啮合动力学方程如下:

(2)

(3)

其中，ms、Js、rs，mpn、Jpn、rpn分别为太阳轮和星轮单侧质量、绕z轴转动惯量、基圆半径。pspnR(t)为人字齿右侧沿齿轮啮合线方向相对啮合位移。sα=sinα,cα=cosα,其余类推。

合并式(2)、式(3)，并整理为矩阵形式：

以太阳轮两侧斜齿之间耦合矩阵推导为例说明左右侧斜齿连接矩阵的推导过程，如图2所示，左右侧齿轮连接无阻尼运动方程如下：

(4)

(5)

其中，kssx、kssy、kssz、kssθ分别表示太阳轮退刀槽的径向、轴向、竖向和旋转刚度。合并式(4)、式(5)，并整理为矩阵形式：

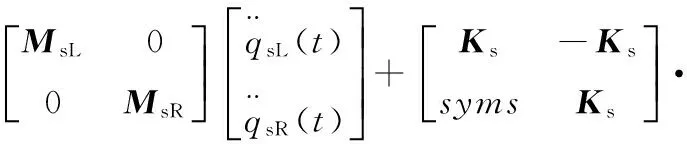
同理得星轮和内齿圈连接矩阵Kp、Kr。

如图3所示，以第n个星轮单侧与星形架耦合为例，导出单边星轮与星形架耦合方程如下：

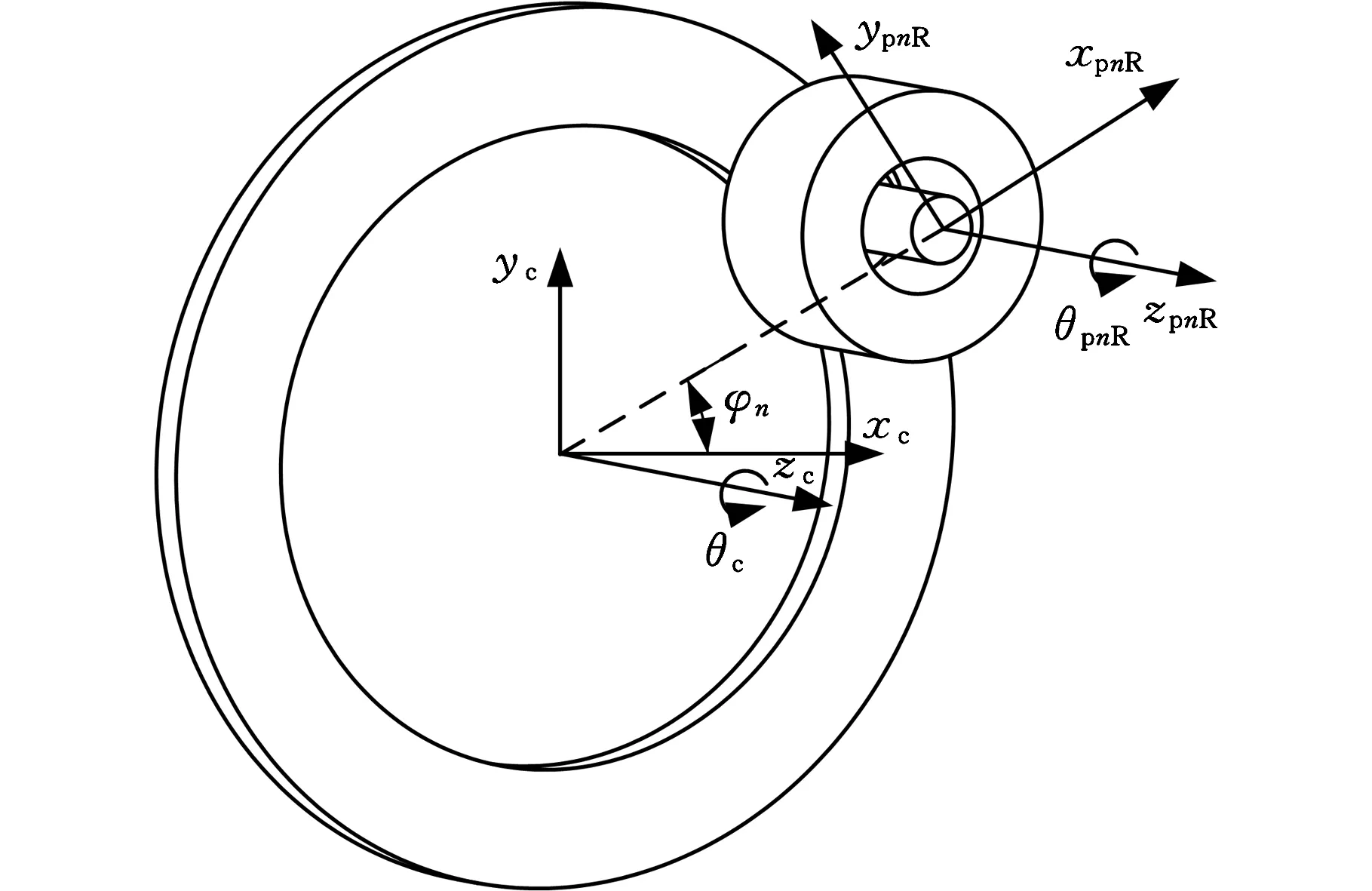
图3 星轮n-星形架耦合动力学模型Fig.3 Dynamic model of star-carriern pair

(6)

(7)

式中，kp、kpz为星轮与星形架之间的径向支撑刚度、轴向支撑刚度；rc为星轮旋转中心至星形架旋转中心距离,rc=rs+rp。

合并式(6)、式(7)，并整理为矩阵形式：

按有限元思想，系统无阻尼自由振动方程如下：

K=Kb+KL+Km

KL=

Km=

Ks=diag(kssx,kssy,kssz,kssθ)

Kp=diag(kppx,kppy,kppz,kppθ)

Kr=diag(krrx,krry,krrz,krrθ)

式中，Kb、KL、Km分别为支撑刚度矩阵、左右侧耦合矩阵、啮合副耦合矩阵；kζ、kζz、kζθ(ζ=c,s,pn,r)分别为构件径向支撑刚度、轴向支撑刚度、轴向扭转刚度,n=1，2，…，N。

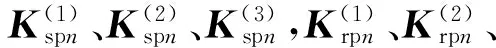
行星人字齿轮传动刚度矩阵与星形传动刚度矩阵区别仅是支撑刚度矩阵Kb中轴向扭转刚度取值不同。对于星形传动,ksθ、krθ为0，kcθ为非0；对于行星传动,ksθ、kcθ为0，krθ非0。因而下文证明对行星传动也是适用的。

2 固有特性规律

表1 传动系统刚度参数

表2 传动系统构件参数

分析固有圆频率及振型，系统模态分为四类，振型如图4所示，图中黑点和实线表示振动振型所决定的构件位置，虚线表示构件静平衡位置。

(1)中心构件轴向-扭转耦合模态18个(重根数r=1)，固有圆频率数值见表3第1栏，振型如图4a所示。振型特征为：中心构件平动振型坐标为0，仅有轴向和扭转；星轮振型相同。

(2)星轮模态8个(重根数r=N-3)，此模态只有当N>3时才会出现，固有圆频率数值大小与星轮个数无关。频率数值见表3第4栏，振型如图4b所示。其振型特征为：中心构件不动；星轮振型成比例变化。

(3)中心构件平动模态7个(重根数r=2)，频率数值见表3第2栏，振型如图4c所示。其振型特征为：中心构件轴扭振型坐标为0，仅有平动；人字齿左右两侧振型z向相反，其他相同。

表3 系统固有圆频率(rad/s)及其重根数与星轮个数关系

(a)中心构件轴向-扭转耦合模态 (b)星轮模态

(c)中心构件平动模态 (d)星轮与中心轮耦合模态图4 星形人字齿轮传动四种模态振型Fig.4 Vibration modes of the double-helical star gear transmission system

(4)星轮与中心轮耦合模态6个(重根数r=2)，频率数值见表3第3栏，振型如图4d所示。其振型特征为：中心构件除星形架不动外，其他平动；同侧星轮振型成比例变化；人字齿左右两侧振型z向相同，其他相反。

前三类模态与LIN等[2]提出的直齿行星齿轮模态相似，第四类模态是由于自由度数增多而产生的全新模态。

3 固有特性规律的证明

为了证明其振型规律，假设系统的固有圆频率为ωk，对应振型为Φk，则

Φk=(Pc，PrL，PsL，P1L，…，PrR，PsR，P1R，…)T

Pξ=(xξ，yξ，zξ，θξ)ξ=
(Pc，PrL，PsL，P1L，…，PrR，PsR，P1R，…)

分块代入整理后可得

(8)

(9)

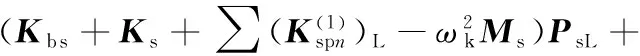
(10)

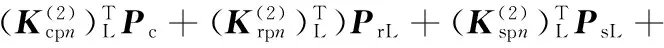
(11)

(12)

(13)

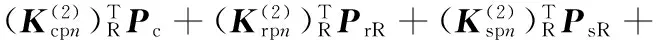
(14)

系统模态的求解问题转化为对式(8)～式(14)特征值ωk及其对应振型的求解问题。

3.1中心构件轴向-扭转耦合模态证明

中心构件轴向-扭转耦合模态的振型特征如下式所示:

(15)

中心构件只有轴扭，同侧星轮的振型相同。

将Φk代入式(8)～式(10)、式(12)、式(13)整理得

(16)

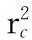
(17)

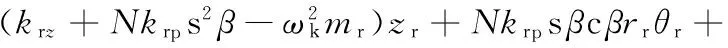
(18)

(19)

(20)

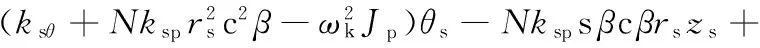
(21)

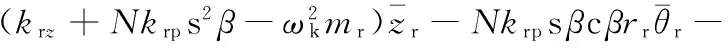
(22)

(23)

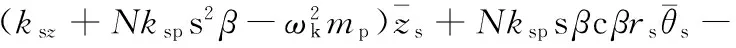
(24)

(25)

将Φi代入式(11)和式(14)得到：

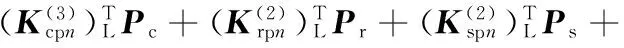
(26)

(27)

系统的固有圆频率求解转化为求解式(15)中所含18个变量的特征值ωk的问题，式(16)～式(27)共有18个方程，联立后可以计算得到18个固有圆频率和其对应振型。

3.2星轮模态证明

此振型的特征如下式所示：

(28)

中心构件不动，单侧星轮成比例运动，其中，λn为常数。

将Φi代入式(8)～式(10)、式(12)、式(13)整理得

(29)

(30)

(31)

(32)

(33)

(34)

(35)

3.3中心构件平动模态证明

3.3.1等价性结论的证明

在证明此模态之前，首先证明以下结论：式(9)～式(11)和式(12)～式(14)对应等价的前提条件是人字齿左右侧振型满足以下两个条件之一。两个条件为：①中心构件平动，左右侧振型z向相反，其他项相同；②中心构件平动，左右侧振型z向相同，其他项相反。由于篇幅限制，仅对振型满足条件①时式(11)和式(14)的等价性进行证明，其他证明过程类似。

式(11)、式(14)中的(Ⅲ)表达式如下：

sψrpncβsβxr+sψspncβsβxs+τκzp-
cψrpncβsβyr+cψspncβsβys=0

(36)

-sψrpncβsβxr+cψrpncβsβyr-τκzp-
sψspncβsβxs-cψspncβsβys=0

(37)

3.3.2中心构件平动模态证明

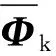
(38)

将Φk代入式(8)～式(10)得

(39)

(40)

(41)

(42)

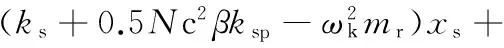
(43)

(44)

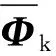
易于证明：

(45)

(46)

3.4星轮中心轮耦合模态证明

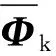
(47)

固有频率个数以及重数证明过程如下。

将Φk代入式(8)～式(10)得出：

(48)

(49)

(50)

(51)

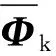
易于证明：

(52)

(53)

星轮振型成比例变化证明过程如下。为了表示方便，引入如下中间变量：

εs=ksp(-sαc2β，-cαc2β，cβsβ，c2βrp)T

εr=krp(-sαc2β，cαc2β，cβsβ，c2βrp)T

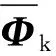
-η(ωk)P1=εs(sαxs+cαys)+εr(sαxr-cαyr)

(54)

(55)

(56)

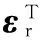
(57)

整理式(56)、式(57)得

(58)

将式(58)代入式(54)、式(55)可得

4 结论

(1)中心构件轴向-扭转模态18个(重根数r=1)。其振型特征为：中心构件平移振型坐标为0，仅有轴扭；同侧星轮振型相同。

(2)星轮模态8个(重根数r=N-3)，此模态只有当N>3时才会出现，固有圆频率数值大小和星轮个数无关。其振型特征为：中心构件不动；同侧星轮振型成比例变化。

(3)中心构件平动模态7个(重根数r=2)。其振型特征为：中心构件仅有平动；人字齿左右两侧振型坐标z相反，其他相同。

(4)星轮中心轮耦合模态6个(重根数r=2)。其振型特征为：中心构件除星形架不动外，其他均只有平动；星轮振型呈比例；人字齿左右两侧振型坐标z向相同，其他相反。

(5)星形传动的四类振型特征同样适用于同自由度数的行星人字齿轮传动系统。

[1] 黄春峰, 姚艳玲, 蒋明夫. GTF发动机技术性能和应用前景分析[J]. 航空制造技术,2012,409(13):34-38. HUANG Chunfeng, YAO Yanling, JIANG Mingfu. Analysis on Technical Performance and Application Prospect of GTF Engine [J]. Aeronautical Manufacturing Technology,2012,409(13):34-38.

[2] LIN J, PARKER R G .Analytical Characterization of the Unique Properties of Planetary Gear Free Vibration[J]. Journal of Vibration and Acoustics,1999,121(7):316-321

[3] KIRACOFE D R, PARKER R G. Structured Vibration Modes of General Compound Planetary Gear Systems[J]. Journal of Vibration & Acoustics, 2007, 129(1):511-526.

[4] PARKER R G. A Physical Explanation for the Effectiveness of Planet Phasing to Suppress Planetary Gear Vibration[J]. Journal of Sound & Vibration,2000,236(4):561-573.

[5] LIN J, PARKER R G. Sensitivity of Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters[J]. Journal of Sound & Vibration,1999,228(1):109-128.

[6] LIN J, PARKER R G. Natural Frequency Veering in Planetary Gears[J]. Mechanics of Structures & Machines,2001,29(4):411-429.

[7] 林何, 王三民, 董金城. 斜齿行星齿轮传动系统振动模式与动载特性[J]. 航空动力学报,2015,30(9):2298-2304. LIN He,WANG Sanmin,DONG Jincheng.Virbration Mode and Dynamical Characteristics of Helical Planetary Gear Train [J]. Journal of Aerospace Power,2015,30(9):2298-2304.

[8] 卜忠红.人字齿行星传动系统的动态特性研究[D].西安：西北工业大学,2011. BU Zhonghong. Research on Dynamic Characteristics of Planetary Gear Train with Herringbone Gears [D]. Xi’an：Northwestern Polytechnical University，2011.

[9] 任菲, 秦大同, 吴晓铃. 考虑制造误差的人字齿行星传动均载特性[J]. 中南大学学报(自然科学版),2016，47(2):474-481. REN Fei, QIN Datong, WU Xiaoling. Load Sharing Performances of Herringbone Planetary Gears Considering Manufacturing Errors[J]. Journal of Central South University (Science and Technology),2016,47(2):474-481.

[10] PRASHANT S. Dynamic Modeling of Double-helical Planetary Gear Sets[D]. Columbus: The Ohio State University,2012.

[11] 王琳杰, 王三民, 欧阳斌,等. 功率四分支齿轮传动弯扭耦合动力学特性研究[J]. 振动与冲击,2014,33(13):161-165. Wang Linjie, WANG Sanmin, OUYANG Bin, et al. Lateral-torsional Coupling Dynamics Characteristics of Power Split Transmission with Four Branches[J]. Journal of Vibration and Shock,2014,33(13):161-165.

(编辑王艳丽)

TheoreticalResearchofVibrationModesforDouble-helicalStarGearTransmissionSystems

HAO Lifeng WANG Sanmin WANG Feiming

1.School of Mechanical Engineering, Northwestern Polytechnical University,Xi’an,710072 2.Shenyang Engine Design and Research Institute,Aviation Industry Corporation of China, Shenyang,110015

Dynamics model and dynamics equations with coupled bent-torsional-axial of a double-helical star gear transmission system was established based on the lumped mass method. The double-helical gears were treated as two helical gears with opposite spiral angle connected by massless spring which had the bending, torsion and axial stiffnesses. The natural cyclic frequencies and vibration modes of the system were calculated. The structure of the vibration modes were well-defined, where the special structure resulted from the cyclic symmetry of the star herringbone gears. Vibration modes were classified into four categories and the multiplicities and numbers of the eigenvalue were analyzed. The results show that the double-helical star gear transmission system has four typical vibration modes: axial-rotational coupled vibration mode (multiplicityr=1), star gear mode (multiplicityr=N-3,N>3), center component translational vibration mode (multiplicityr=2), star gear and center gear coupled mode (multiplicityr=2).

double-helical star gear; transmission system; coupled vibration mode; star gear mode; translational vibration mode

2016-04-08

TH133

10.3969/j.issn.1004-132X.2017.17.014

郝立峰，男，1992年生。西北工业大学机电学院硕士研究生。主要研究方向为齿轮传动系统减振降噪。王三民，男，1960年生。西北工业大学机电学院教授、博士研究生导师。王飞鸣，男，1978年生。中国航空工业集团公司沈阳发动机设计研究所高级工程师。