非对称Y型大悬臂式混凝土结构的地震响应分析

刘 豹，袁新明，房 媛

(1.扬州大学 水利与能源动力工程学院， 江苏 扬州 225009； 2.合肥工业大学 建筑设计研究院， 安徽 合肥 230009)

非对称Y型大悬臂式混凝土结构的地震响应分析

刘 豹1，袁新明1，房 媛2

(1.扬州大学 水利与能源动力工程学院， 江苏 扬州 225009； 2.合肥工业大学 建筑设计研究院， 安徽 合肥 230009)

非对称Y型大悬臂式混凝土作为一种新兴的工程结构，在桥梁结构工程中得到广泛的应用。对地基-大悬臂混凝土结构建立了三维模型，并运用有限元的动力分析方法，对其进行了动力响应分析，得到混凝土结构悬臂端在地震波时刻的位移响应和应力响应，分析了在三种抗震烈度下，结构悬臂端的行为，为工程抗震性能评估提供了参考依据。

非对称Y型大悬臂结构；地震波；动力分析；位移；应力

非对称Y型大悬臂式混凝土作为一种新兴的工程结构，由于结构墩体占地面积较小，向上延伸后，在下部留下空间较大。在工程实际中得到广泛的应用。文献[1]得出了水平与竖向组合的地震作用下，大跨度钢管混凝土拱桥的地震响应；文献[2]探讨了以不同钢结构加层方式对悬臂梁动力特性的影响规律，对可能出现的薄弱层部位提出抗震加固方案与措施；文献[3]对T型钢筋混凝土框架结构进行地震作用分析，找出了结构的薄弱层，判断出结构抗震性能；文献[4]研究了桩-土-结构共同作用对多跨连续刚架拱桥地震作用下结构内力分布产生不利影响。本文通过建立地基-大悬臂混凝土结构三维模型，对其进行弹性时程分析，侧重于分析悬臂端在地震波时刻的位移和应力响应，研究结果为其抗震性能评估提供参考依据。

1 有限元非线性动力分析方法

本文基于ABAQUS有限元软件对非对称Y型大悬臂式混凝土结构进行分析，由文献[5]可知对大悬臂结构形成质量矩阵M、阻尼矩阵C、刚度矩阵K和外部荷载的作用P。即

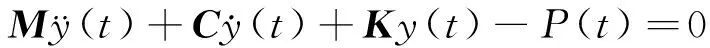
(1)

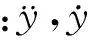
对于离散化的有限元体系，对应相应的时间，可以建立n个动力平衡方程，本文采用Newmark-β法对结构的位移、速度和加速度进行直接积分。

在t和t+Δt时刻，结构体系非线性的动力平衡方程可表示为

(2)

(3)

利用Newmark法求解得出在t+Δt时刻的位移和速度向量可表示为

(4)

(5)

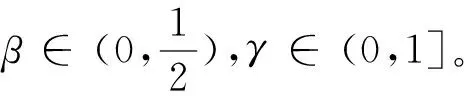
2 工程算例

2.1 大悬臂结构

某Y型大悬臂式大门，总长度为22m，长悬臂一侧高7.2m，短悬臂一侧高6.2m，宽为7.2m。基础采用C25混凝土结构，其长4.5m、高1.2m、宽6.6m，墩体和悬臂结构采用C35混凝土材料，最右侧为Q335方管空心材料，长3m，厚度2cm，外层以素混凝土饰面。地基为黏性土材料，根据G.M.萨布尼斯等结构模型实验得出的结论，地基尺寸取1～5倍的基础结构尺寸就能反应出无限地基对基础结构的影响。考虑到人工动力边界条件，故基础长取15m，宽取15m，深度取3.5m。具体结构尺寸见图1、图2、图3。

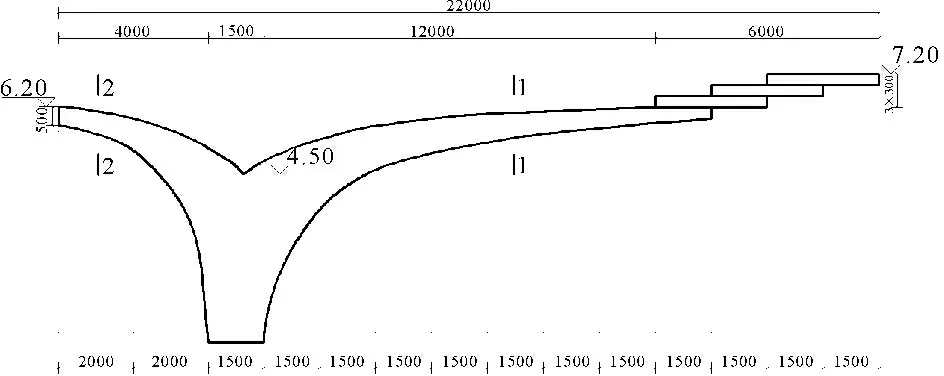
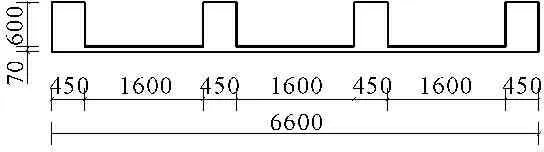
图1 立面图(单位：cm)

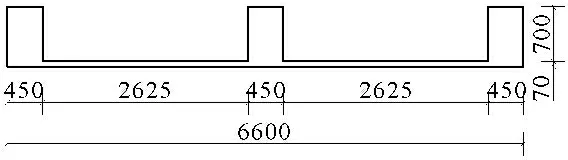
图2 1-1断面图(单位：cm)

图3 2-2断面图(单位：cm)

2.2 材料参数

本大悬臂结构的主体采用C30混凝土、C25混凝土和Q235轻钢等线弹性材料。其材料的力学参数见表1。

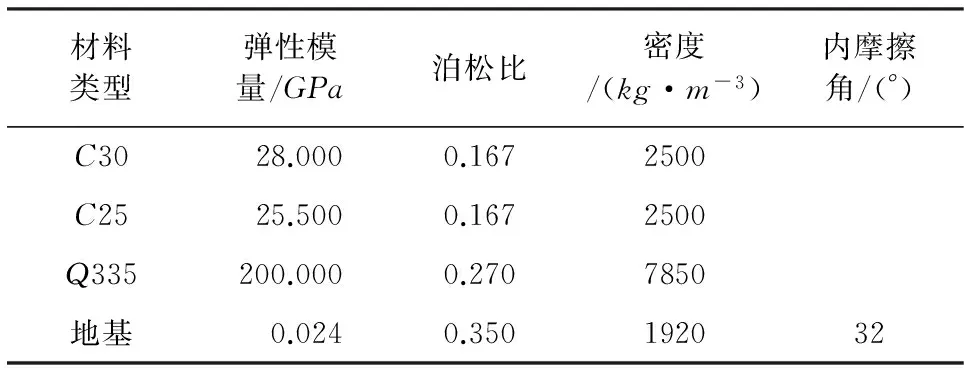
表1 材料的力学参数

2.3 地基与结构的相互作用

将边界条件施加在模型上，主体与基础设置为摩擦接触，基础与地基之间设置为表面与表面接触，地基底部设置为固定端。其中，在结构与地基接触上，在接触表面的法向上采用 “硬”接触模型，在接触表面的切向上采用罚函数摩擦公式，其基本思想是库仑摩擦理论，即：

τ临界=μP

(6)

式中：τ临界是切应力临界值；μ是地基的摩擦系数；P是接触面上的法向压力。

当切应力大于其临界值τ临界时，接触面开始产生相对位移，否则，则处于相对静止状态。

2.4 网格的划分

因为本结构的悬臂段多为不规则弧形结构，为了更快速的进行有限元分析，故本结构直接采用二次四面体C3D10单元划分网格。

本结构共划分32 770个C3D10类型单元，节点总数为57 280个。其中大悬臂主体结构共包含26 808个二次四面体，47 692个节点；基础部分共包含404个二次四面体C3D10类型单元，753个节点；地基部分共包含5 558个二次四面体C3D10类型单元，8 835个节点。模型网格划分情况如图4所示。

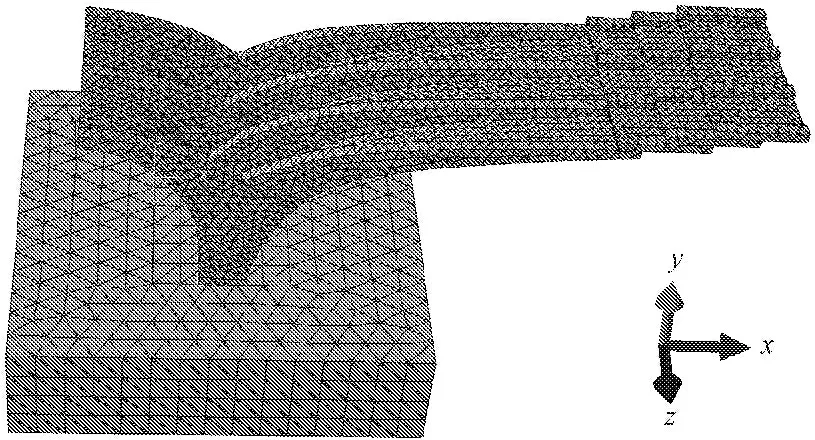
图4 非对称Y型大悬臂式网格划分

2.5 地震波的选择

地震波的选取要满足地震动的三个条件：(1) 频谱特性； (2) 有效加速度峰值； (3) 持续时间较长。

根据规范[6]可得，算例设计地震分组为第二组，场地类别为Ⅱ类，特征周期Tg=0.4 s。为了避免相似地震波对研究带来的误差，本文选取的是典型的频谱特性差别较大的强震记录，即印度Koyna地震波。选取其中包含峰值并且频谱特性较多的前10 s，记录时间为0.02 s，主频范围在2.5 Hz～3.5 Hz之间。水平方向在3.13 s时出现峰值加速度，为473.78 cm/s，竖直方向在3.8 s时出现峰值加速度，为311.56 cm/s。

3 计算结果分析

3.1 大悬臂结构模态分析

结构模态分析是进行动力学分析的基础，能反映出结构对于不同荷载动力响应的模态。在ABAQ US中定义一个线性摄动步，假设结构为自由振动，忽略外部荷载作用，选取前6阶振型进行分析，得到结构的固有频率、振型参与系数[7]和有效模态质量等，具体分析结果如表2所示。

表2 非对称Y型大悬臂式混凝土结构振型特征

注：下划线部分为选取的数值。

由表中数据得到本结构的自振频率是1.883 Hz,其中从振型参与系数的分布来看，模态3在z方向的系数为1.509，远远大于其他z方向的系数，其有效模态质量之和占总质量的89.8%，即模态3在z方向荷载上响应比较大；模态5在x方向的系数分别为-2.011，其有效模态质量之和占总质量的77.5%，即模态5在x方向荷载上响应比较大。在时程分析法采用瑞利阻尼方法计算，即：

[C]=α[M]+β[K]

(7)

(8)

(9)

式中：ωi、ωj表示第i阶、第j阶振型的圆频率；ζi、ζj表示第i阶、第j阶振型的阻尼比，一般取ζi=ζj=ζ=0.05。

由表2中数据得到对本结构影响较大的频率在7.203 Hz、12.217 Hz，分别带入公式计算出瑞利阻尼系数α=0.453,β=0.0026。

3.2 大悬臂结构地震响应分析

3.2.1 地震波归一化处理

该大悬臂结构的设防烈度为8度，本文在计算其受多遇地震作用时，分别选取7度、8度和9度的抗震设防烈度把原地震波按式(10)处理成不同震级。

(10)

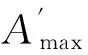
3.2.2 位移响应分析

在计算中沿结构x方向和y方向从外部文件中以RAW模式读入地震波。选取最不利情况，即叠梁最右为分析对象，其位移响应如图5、图6所示。

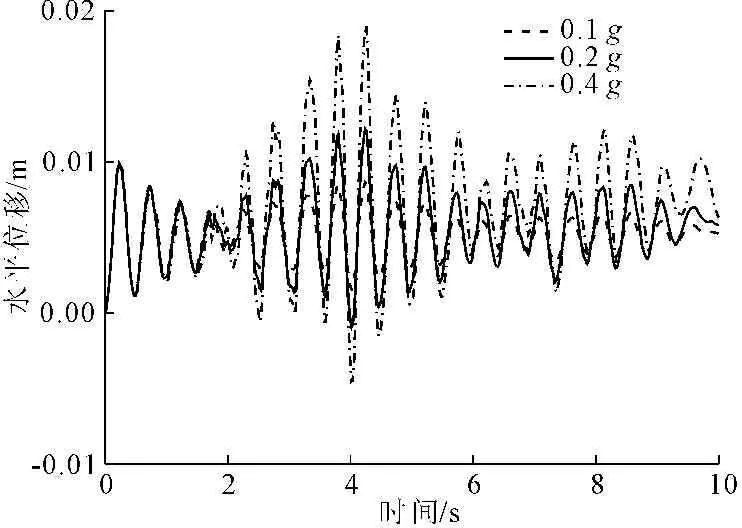
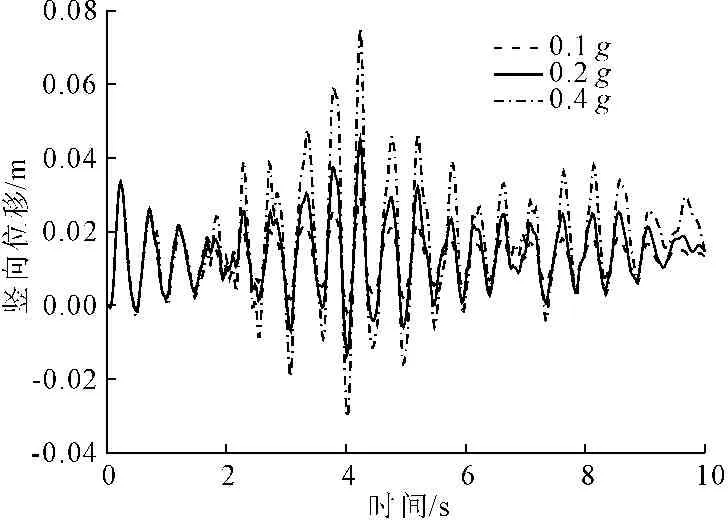
图5 水平位移响应

图6 竖直位移响应

对计算结果进行分析，得到叠梁最右端的水平位移特征值、竖直位移特征值、其残余位移以及对应的时间。具体分析结果如表3所示。

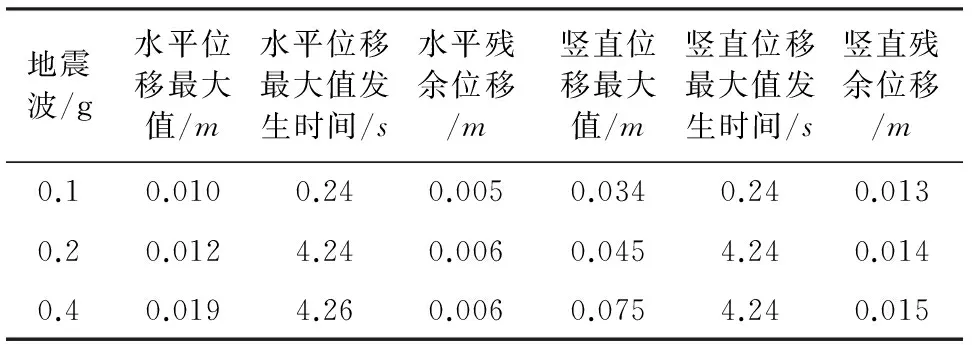
表3 位移响应极值表

由表3可知，水平方向上，叠梁右端的位移响应随地震波的增大而增大，但残余位移增加速度较为平缓；竖直方向上，叠梁右端的位移响应随地震波的增大而增大，残余位移增加速度也较为平缓；在相同的地震波下，叠梁右端的竖向位移明显大于水平位移，残余位移也响应增加。

根据规范计算，此悬臂构件的容许挠度值为2l/400=0.075 m。在0.4g时，悬臂端的综合位移为0.77 m，大于容许挠度值。

3.2.3 应力响应分析

在地震波未施加时刻，结构的最大主应力出现在悬臂结构悬臂中上部，第20 924节点；最小主应力出现在悬臂结构第334节点，故本次应力分析主要研究这两个节点的时程变化。如图7、图8所示。

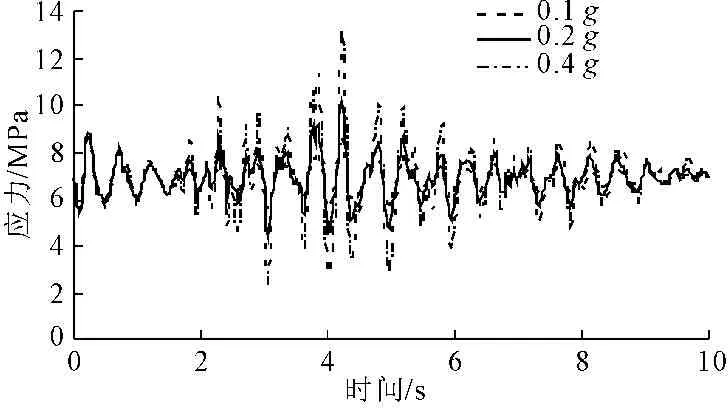
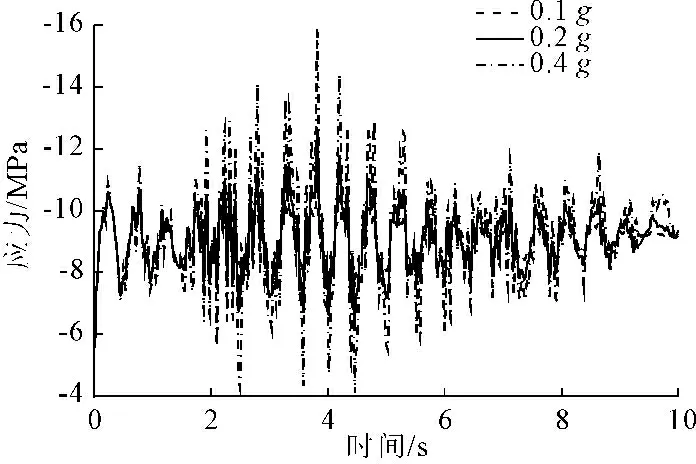
图7 最大主应力曲线

图8 最小主应力曲线

对计算结果进行分析，得到这两个节点最大主应力特征值和最小主应力特征值以及其对应的时间。具体结果如表4所示。

表4 应力响应极值

由表4可知，节点的最大主应力在0.4g地震波的3.06 s时刻有最小值，为2.16 MPa，其拉应力也超过C35混凝土的轴心抗拉强度设计值，为1.57 MPa，所以需要进行配筋。节点最小主应力在0.4g地震波的3.82 s时刻有最大值，为15.9 MPa，其压应力未超过C35混凝土的轴心抗压强度设计值，为16.7 MPa，所以结构不会产生压应力破坏。

4 结 语

本文选取悬臂叠梁最右端为位移分析对象，在0.1g和0.2g的地震波作用下，其综合位移未超过规范容许挠度的要求，即在设防烈度为7度和8度的情况下，悬臂端满足挠度的要求；而在0.4g的地震波作用下，其综合位移超过规范容许挠度的要求。即在此情况下，需要采取减轻材料自重或者增加材料刚度等工程措施，以避免构件破坏。

[1] 王沛耘.大跨度钢管混凝土拱桥自振特性及地震响应分析[D].成都:西南交通大学,2008.

[2] 戴 宁.带悬臂梁的现有建筑采用钢结构加层的抗震性能研究[D].南昌:南昌航空大学,2015.

[3] 陶正宇.T型不规则钢筋混凝土框架结构抗震性能分析[D].合肥:安徽建筑大学,2016.

[4] 李法雄,聂建国,樊健生.多跨连续钢筋混凝土刚架拱桥的抗震分析[J].工程力学，2010,27(12):179-180.

[5] 沈聚敏,高晓旺,周锡元,等.抗震工程学[M].北京:中国建筑工业出版社，2000:90-92.

[6] 中国建筑科学研究院.建筑抗震设计规范：GB 50011—2010[S].北京：中国建筑工业出版社，2010:313-314.

[7] 吴 浩.结构非线性时程分析输入地震波选择方法[D].大连:大连海事大学,2016.

Seismic Response Anaylsis of Non-symmetric Y-type Cantilever Concrete Structure

LIU Bao1, YUAN Xinming1, FANG Yuan2

(1.CollegeofHydraulicEnergyandPowerEngineering,YangzhouUniversity,Yangzhou,Jiangsu225009,China; 2.HefeiUniversityofTechnologyInstituteofArchitecturalDesign,Hefei,Anhui230009,China)

As a new engineering structure, non-symmetric Y-type concrete structure has been widely applied in bridge engineering. In this paper, the three dimensional of large cantilever concrete structure is analyzed by finite element dynamic analysis method. The displacement response and stress of the concrete cantilever are obtained, at the same time, the behavior of concrete cantilever is analyzed under three different seismic intensity.

non-symmetric Y-type concrete structure; seismic wave; dynamic analysis; displacement; stress

10.3969/j.issn.1672-1144.2017.04.035

2017-03-27

2017-04-20

刘 豹(1992—)，男，江苏徐州人，硕士研究生，研究方向为水工钢结构。E-mail:1450753978@qq.com

袁新明(1958—)，男，河南新野人，博士，教授，主要从事水工钢结构方面的研究工作。E-mail:yuanxm@163.com

TU37

A

1672—1144(2017)04—0178—04