节段模型二元端板合理尺寸估算方法
2023-01-31刘博祥姬乃川李加武
白 桦, 刘博祥, 姬乃川, 李加武
(1. 长安大学 公路学院,西安 710064; 2. 陕西省交通规划设计研究院,西安 710065)
桥梁结构一般为柔长结构,沿顺桥向尺寸较大,而其他两个方向尺度小很多。所以风对桥梁结构的作用近似满足片条理论,可通过节段模型风洞试验来研究桥梁结构的风致振动响应。节段模型风洞试验基于片条理论假定,认为来流经过模型时的流动属于二维流动。因此设置二元端板是桥梁节段模型抑制端部三维绕流效应的一个重要手段。由于桥梁节段模型要进行测振试验,二元端板尺寸过小无法有效抑制三维绕流的干扰,尺寸过大可能造成节段模型的质量超限或不好调整模型扭弯频率比。我国JTG/T 3360-01—2018《公路桥梁抗风设计规范》中建议当模型长宽比小于4时可设置端板来保证节段模型的二元流动特性,但并没有规定二元端板的具体尺寸和形状。因此有必要针对桥梁节段模型的二元端板设置方法开展研究,为节段模型二元端板的尺寸设计提供参考。
对于端部效应抑制,依然采用设置端板的办法。圆形断面和矩形断面是常见典型的断面,在工程应用中非常广,设置端板可以减轻端部效应对圆形节段模型和矩形节段模型风压系数沿展向的分布的影响,有端板时分布更为均匀[1-2]。Obasaju[3]通过试验发现采用小尺寸端板时,背风面吸力的绝对值比无端板时降低,采用大尺寸的端板时,背风面吸力的绝对值比无端板时增加;Kubo等[4]研究了端板尺寸对端部效应的影响机理,当未设置端板或者端板尺寸较小时,由于模型沿展向内侧和外侧气压的不同,导致气流沿模型展向从高压向低压流动,当设置较大尺寸端板后,能够有效的防止外侧气流和端板之间气流的相互流动,保证端板之间气流的二维特性;Morse等[5]发现端板的安装会使节段模型涡振响应更加稳定。
国内对节段模型风洞试验端部效应的研究较少。郑云飞等[6-7]研究了不同端板尺寸对宽高比为1、5和10的二维矩形断面和斜拉索断面的气动力、风压分布情况影响,结果表明:端板对端部效应可以起到有效的抑制作用,端板尺寸较小时不能保证模型二维流动特性,并且最小端板尺寸随风攻角的增大而增大;白桦等[8]选用流线形和钝体两种主梁断面进行测力与测压试验,对比模型长宽比和二元端板形式的变化对试验结果的影响,结果表明:较大的端板能更好的实现二维绕流,二元端板的宽度建议取主梁宽度的1.4倍以上;高斐[9]通过研究研究端板外形、尺寸对流线形断面和钝体断面的影响,发现对于这两种断面,端板尺寸相对主梁较小时,无法抑制端部三维绕流场的干扰,端板尺寸较大时,所测得的三风力系数趋于稳定;温青等[10-11]研究了不同长宽比、展弦比和端板尺寸的节段模型的气动特性,发现节段模型上的气动力展向分布具有显著的端部效应,增加端板有助于提高流场的二维特征;燕翔等[12]研究了不同端板条件下的圆柱涡激振动响应,发现设置端板有利于能量汲取,无端板不适用于流致振动能量利用。
尽管关于二元端板对节段模型试验结果影响已经取得了一些进展,但上述研究关于端板尺寸的设置主要依据经验,缺乏合理端板尺寸估算方法的指导。这就有可能导致端板尺寸过大造成模型超重或扭转频率不好调试,及过大端板导致刚度下降引起振动或端板尺寸过小无法抑制端部绕流干扰而引起试验误差。本文针对节段模型试验常用的矩形端板,给出一种矩形端板尺寸的取值思路,依据此方法可以估算二元端板的合理尺寸,最后结合风洞试验检验依据此方法确定端板尺寸的合理性。
1 端部效应作用机理
端板的设置对节段模型端部效应有一定地抑制作用,利用计算流体力学(computational fluid dynamics,CFD)数值模拟的方法对抑制作用机理进一步解释。为研究端板对模型周围气流流动的影响,分别建立无端板和有端板的节段模型,断面为宽高比(B/H)10的矩形三维断面,模型长宽比为2,端板尺寸为22H×12H,设置为面,端板厚度影响可忽略[13]。
1.1 计算域设置
计算域流场设置为20B×40B×4B长方体,如图1所示,模型迎风面距离流场入口10B,背风面距离流场出口30B,下游尾流区尺寸大于上游是为了保证尾流充分发展。模型两侧距离流场两侧壁面距离不小于B,以确保模型端部流动的计算结果不受风场边界的干扰,阻塞率小于5%,可以忽略边界对流场计算结果的影响。

图1 计算域设置Fig.1 Calculation domain setting
1.2 边界条件
来流入口边界设置为velocity-inlet(速度入口);尾流出口边界设置为pressure-outlet(压强出口),由于出口和大气相通,其静压值设为0,该方法相比outflow(出流)具有容易收敛的优点;与来流方向平行的四个侧面为symmetry边界,该边界法向速度为0,法向梯度为0,但切向速度不为0;计算节段模型表面及端板边界为no-slip wall(无滑移壁面边界),该边界壁面切应力和速度均为0。
1.3 计算结果
由图 2可见,节段模型无端板时尾流处负压区的大小沿展向分布不均匀,自跨中向端部逐渐减小,减小的原因是端部外的气流进入模型的尾流负压区,从而减小了端部尾流负压区尺度。端部尾流处气流没有与模型展向完全垂直,具有明显的展向速度分量;端部迎风处的气流也存在着展向分量,但其幅度要明显小于尾流处的展向分量;在节段模型上加装端板后,端部尾流处负压区尺寸明显增大,整个节段模型尾流负压区的大小沿展向分布更加均匀。这是因为,端板挡住了气流在端部外向模型尾流处的流动,端部迎风处和尾流处的气流流动方向与来流方向一致,垂直于模型展向。

图2 端板对节段模型周围流场的影响Fig.2 Effect of end plate on flow field around segmental model
提取出2个模型阻力系数的展向分布,如图 3所示,端板对模型阻力系数沿展向的分布有很大的影响。无端板时端部阻力系数随展向位置的变化发生明显变化,靠近端部时明显增大,跨中区域阻力系数沿展向呈均匀分布;有端板时,端部阻力系数沿模型展向的变化幅度明显降低,阻力系数沿整个模型展向呈均匀分布。且加端板不仅对端部区域有影响,对跨中区域的模型阻力系数也有影响,原因是在无端板时,端部绕流的实际作用区域不仅仅局限于端部,也会波及跨中,虽然端部绕流对模型跨中部分气动力系数展向分布影响较小,但并不意味着没有影响。
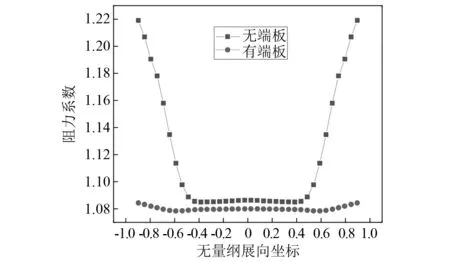
图3 有端板和无端板节段模型的展向阻力系数分布对比Fig.3 Comparison of spanwise drag coefficient distribution between segmental models with and without end plates
2 二元端板尺寸估算方法
桥梁节段模型端板形式选择对称安装的矩形端板,模型断面形心与矩形端板的形心重合,设计时需要确定端板的长宽。CFD数值模拟能较好地再现桥梁断面周围的流场绕流情况,借助CFD方法给出二元端板尺寸估算。
2.1 CFD二维计算
建立试验断面的二维CFD模型,如图 4所示。以断面形心坐标为原点(0,0),在XY平面内建立几何模型、设置边界条件、进行网格划分和求解,得到速度场,如图 5所示。
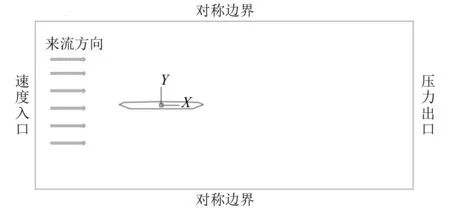
图4 模型布置和边界设置Fig.4 Model and boundary conditions

图5 速度场分布Fig.5 Velocity distribution
2.2 估算模型
流体经过模型表面时,模型周围的流速不尽相同,模型端部以外区域的空气流动速度与远处来流相一致,气流不会受到模型的干扰。
如图 6所示,可直观的观察到模型受端部效应影响的区域,而在模型中间部分不会受到端部效应的影响。为验证这一点,在三维模型中选择与来流方向平行的两个切面,切面位置如图7所示,A切面位于模型跨中,B切面位于模型端部以外。A切面不受端部效应影响,主要表现为二维绕流,不受展向流动干扰,这与二维模拟的模型表面流场基本一致,因此从简化计算及准确性角度考虑,建立估算模型时,可利用试验断面的二维CFD模型得到的速度场,其网格数量少,计算速度快,对计算机配置要求较小,是一种快速且有效的计算模型。

图6 三维流线形箱梁CFD模型计算Fig.6 CFD model calculation of 3D streamline box girder
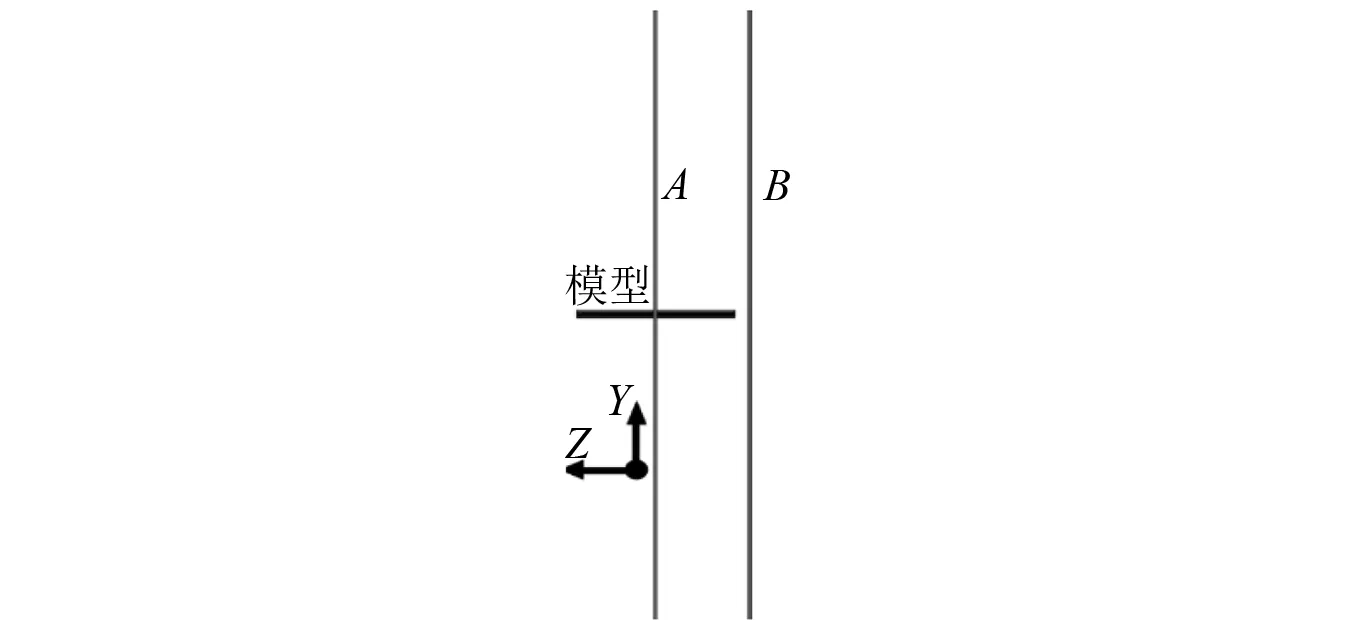
图7 三维模型切面位置示意(来流方向为X方向)Fig.7 Section position of three-dimensional model (Inlet flow direction is X direction)
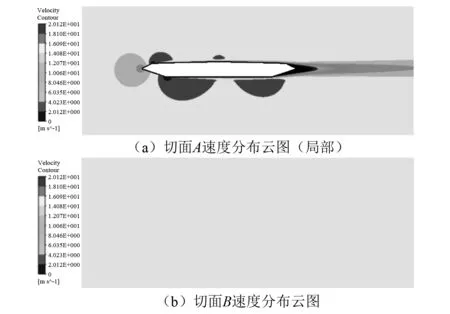
图8 A、B切面速度分布图Fig.8 Velocity distribution in section A and B
由切面A的速度分布图可知,该切面模型周围的流速不尽相同,而切面B各处风速相同。在模型断面附近,A和B切面在相同(x,y)位置处的流速不相同,由此产生的流速差导致断面沿展向不同位置存在气压差,这种气压差会导致气流沿模型展向流动,造成三维绕流干扰。在此基础上,利用端部内外流速差计算出两者的动压差,为便于参数的分析,将其无量纲化得到压力差的分布,即F(x,y),公式如式(1)所示。F(x,y)表示(x,y)位置气流沿展向流动的强度,该值越大,展向流速越大,产生的动压差越大,对二维效应的干扰就越严重。
(1)
式中:ρ为空气密度1.225 kg/m3;U(x,y)为二维CFD模型中(x,y)坐标处的流速,m/s,其中(0,0)坐标为模型的形心;U0为模型端部以外区域的流速,即模型入口处的流速。
在两点F(x1,y1)和F(x2,y2)值相等时,距离模型断面较远位置的展向空气流动对气动力的影响会较小,因此必须在F值的基础上考虑距离因素的影响,采用一个考虑距离因素的系数K来进行修正。
d(x,y)为(x,y)点与模型之间的无量纲距离,通常模型尺寸越大,受模型气动外形影响的气流区域就越大,受影响气流区域产生的压力变化就成为了展向流动产生的原因。因此无量纲距离d(x,y)中特征尺寸的定义需考虑节段模型的宽度B和高度H,如式(2)所示。
(2)
当在同一F值下,两个点位置不同时,距离模型较远的点对端部绕流的影响较小。因此定义修正系数K如下:当一点与模型形心的距离为0时,此时展向流动将直接作用在模型上,该点对应的修正系数K为1;而当一点与模型距离趋于无穷远时,展向流动不再对模型的端部绕流产生影响,该点对应的修正系数K为0。假定d(x,y)与该点对应的修正系数K(x,y)值成反比例函数关系(如图9所示),计算式如(3)所示。

图9 d与K的函数关系式Fig.9 Functional relationship between d and K
(3)
引入参数P(x,y)来反映(x,y)位置处气流产生的三维绕流对模型气动力的影响,P(x,y)为修正后的F(x,y),如式(4)所示。P(x,y)值越大,该位置气流的展向流动对端部效应的贡献就越大,即可用来评估端部效应强度。
(4)
2.3 端板合理尺寸
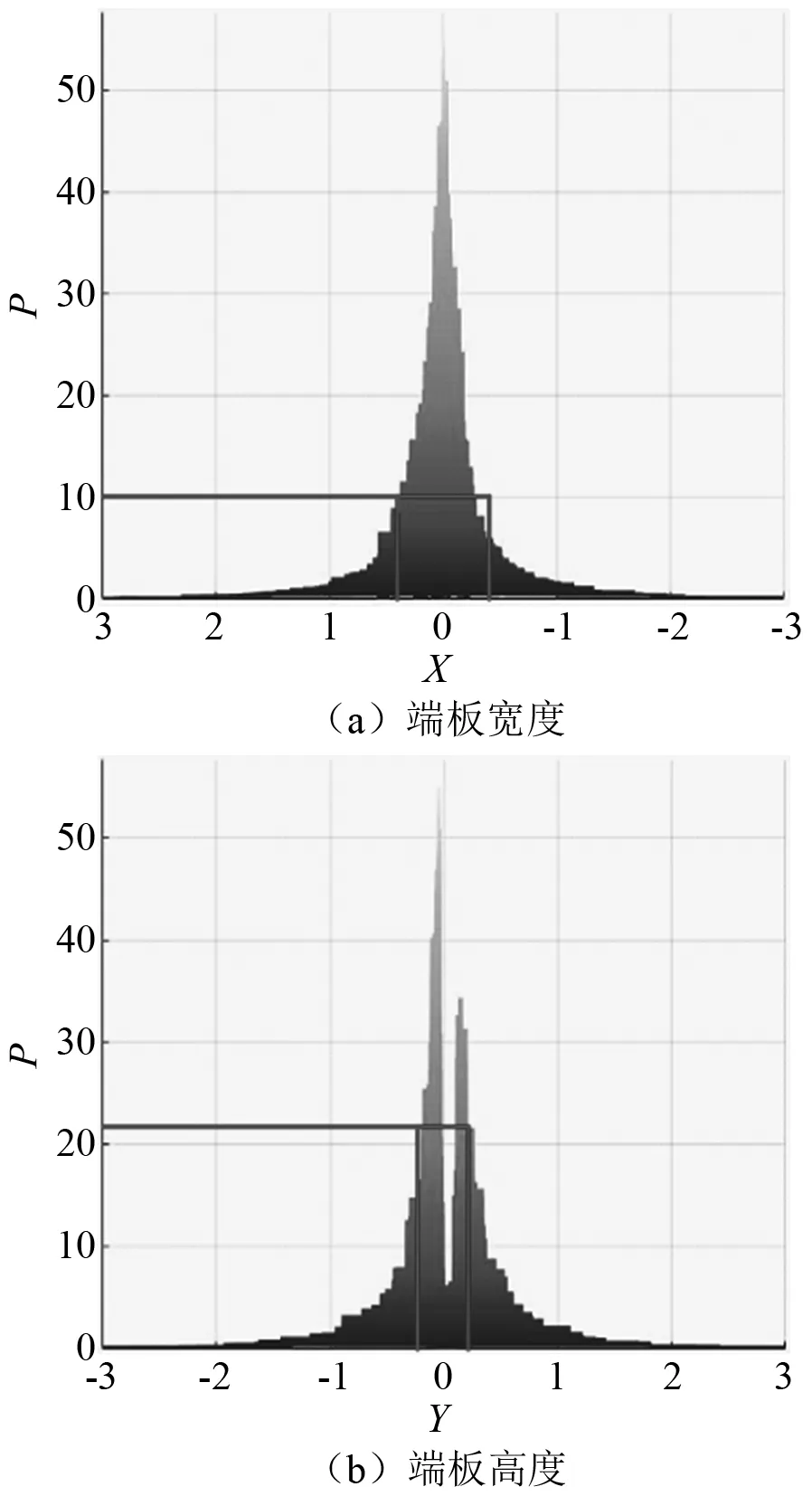
式(4)计算出的P(x,y)分布的三维曲面图如图 10所示。纵轴为P值,模型周围(即(0,0)点附近)的P值要明显大于其他区域,为了让端板充分发挥作用,就必须用端板完全阻挡其所在区域的横向流动。因此,需要在曲面图中P值较大的区域设置端板,而P值较小的区域则不设置端板,但对于P较大较小并没有做出明确界限,所以需要一个临界值P0作为判断依据。临界值P0作为展向流动对模型气动力影响的临界值,P(x,y)>P0的位置需要设置端板来阻挡展向流动,P(x,y) 图10 P(x,y)分布图Fig.10 P(x,y) distribution 给出图10曲面沿x和y方向的视角图,如图11所示。图11(a)中选择P(x,y) 图11 端板合理尺寸建议值Fig.11 Recommended value of reasonable size of end plate 节段模型试验在长安大学CA-1大气边界层风洞中进行,试验风速为15 m/s,均匀流场。模型为宽度0.32 m,高度0.032 m的流线形断面。二元端板的尺寸为:长22H,高12H,其中H为模型高0.032 m,如图12所示,该端板尺寸的选择取自郑云飞等所推荐的端板尺寸。采用3 mm厚的亚克力板制作而成,端板具有足够的刚度,不会在风荷载作用下出现振动。端板安装在法兰盘和模型之间,试验模型如图13所示。为了检验长宽比及设置端板对试验结果的影响,共进行了四种试验工况,分别为:①流线形箱梁长宽比为1,无端板;②流线形箱梁长宽比为1,有端板;③流线形箱梁长宽比为4,无端板;④流线形箱梁长宽比为4,有端板。 图12 二元端板尺寸示意(H为梁高)Fig.12 Schematic diagram of dimension of binary end plate (H is beam height) 图13 加端板和无端板的节段模型图Fig.13 Segmental model with end plates and segmental model without end plates 图14给出了四种工况节段模型测力试验结果。图中可以看出:理论上只要断面外形相同,不同工况无量纲的三分力系数应该保持一致。由于模型端部效应影响、长宽比影响[14]及模型测试设备安装误差等因素影响,不同工况的三分力系数存在一定波动,很难完全重合[15]。长宽比为4的节段模型有端板和无端板三分力系数试验结果基本相同,说明当长宽比较大,端部效应对气动力所产生的干扰占模型总气动力的比重很小,故长宽比4模型的结果可近似视为真值。长宽比越大,端板发挥的效果越小。长宽比为1的节段模型有端板和无端板三分力系数试验结果有明显差异。长宽比为1无端板三分力系数与真值有明显差异,但长宽比为1有端板的结果与真值比较接近。说明二元端板可有效改善长宽比为1的流线形节段模型端部效应。这个端板尺寸大于或等于该断面的合理端板尺寸。 图14 节段模型测力试验结果Fig.14 Force test results of segmental model 每种断面在每一个风攻角下都对应着一个合理端板尺寸,随风攻角的增大,断面所对应的合理端板尺寸也在随之增加。此处提取郑云飞等节段模型测力试验中10°风攻角的结果,得到每种断面在此风攻角的合理端板尺寸(如表1所示)。其中,P0X和P0Y值的确定采用已有的试验结果为基准,通过算例反算得出。 表1 郑云飞等试验中的矩形断面合理端板尺寸Tab.1 Reasonable end plate size of rectangular section in Zheng et al 相比于流体断面,矩形断面的通过性较差[16-18],端部效应更为明显,反算出来的合理P值运用于流体断面所得到的合理端板尺寸偏大,可有效地抑制端部效应,故可以以矩形断面反算出的合理P值可作为标准来考虑。为确定P0X和P0Y,计算了宽高比分别为1、5、10的矩形断面在+10°风攻角的速度分布,计算模型如图15所示。 图15 不同宽高比矩形断面计算模型Fig.15 Calculation model of rectangular section with different aspect ratio 通过上述方法得到不同宽高比矩形断面P(x,y)值的二维分布,将表1中试验所得的合理端板尺寸代入图16~图18中,反算出满足试验要求的最大P值,如表2所示。由此可见:对于宽高比=1的矩形断面,依据郑云飞等所给出合理端板尺寸建议值反算得到的P0X=12,P0Y=17.5。宽高比=5时,P0X=16,P0Y=15,宽高比=10时,P0X=10,P0Y=21.5。模型长宽比越大,端部受三维绕流的影响区域应越大,所需要的端板尺寸也应越大。郑云飞等研究中在宽高比=5和宽高比=10时建议的端板高度均是10H,所以导致宽高比=10时的P0Y值偏大,为21.5。由前面的推导可知:P值越大,该位置气流的展向流动对端部效应的贡献 图16 宽高比=1矩形模型端板尺寸对应P值Fig.16 P value of end plate size of rectangular model when aspect ratio is 1 图17 宽高比=5矩形模型端板尺寸对应P值Fig.17 P value of end plate size of rectangular model when aspect ratio is 5 图18 宽高比=10矩形模型端板尺寸对应P值Fig.18 P value of end plate size of rectangular model when aspect ratio is 10 表2 各矩形断面对应的P0值Tab.2 P0 value of each rectangular section 就越大。所以为了避免因仅凭经验确定端板尺寸,应该把评价指标量化。结合郑云飞等的试验反算出的P值,保证不同断面减小三维绕流效应的标准统一,建议模型宽度方向P0X=10,模型高度方向P0Y=15时,所得到的端板尺寸即可保证端部效应有效抑制。 对3.2节得到的合理P0X=10和P0Y=15,结合流线形模型的试验结果加以检验。 如图19建立3.1节+10°风攻角流线形断面的二维模型,绘制P值曲面图并给出其垂直于X轴和Y轴的视角。将P0X=10和P0Y=15代入图中,得出此状态的合理端板尺寸,如图20所示。 图19 流线形箱梁断面数值模型Fig.19 Model of streamline box girder section 由图20可得,依据上述标准得到流线形箱梁断面合理端板高度0.38 m(11.9H),合理端板宽度0.53 m(16.6H)。3.1节中节段模型风洞试验端板高度12H>合理端板高度11.9H,端板宽度22H>合理端板宽度16.6H。由3.1节的试验结果可知,试验采用的高12H、宽22H的端板基本可以抑制端部的三维绕流效应,端板宽度还稍有富裕。在条件受限的情况下,可以把端板宽度减小到17H,也可以抑制端部的三维绕流效应。本文的方法可以为确定二元端板的合理尺寸提供借鉴。 图20 流线形箱梁模型端板尺寸建议值Fig.20 Recommended value of end plate of streamlined box girder model 通过上述研究确定了合理端板尺寸的P0X和P0Y值,在以后的节段模型设计中可以采用以下流程确定试验断面端板尺寸。 ①建立试验断面的二维CFD模型,计算得到速度场。 ②根据式(4)计算得到试验断面的P(x,y)值,绘制P(x,y)沿X轴和Y轴分布图。 ③由P0X=10和P0Y=15分别得到X轴和Y轴坐标,这两个坐标值就是二元端板的合理宽度与高度。 采用以上方法只需二维试验断面的速度场数值计算即可便捷得到二元端板合理尺寸。 本文通过对端板作用机理的分析,提出一种估算节段模型二元端板合理尺寸的方法作为风洞试验时选取端板尺寸的一种方法,并给予验证,得到以下结论: (1)端部效应是由于模型端部沿展向内外侧流速不同,导致断面沿展向不同位置存在气压差,致使气流沿模型展向流动,造成三维绕流干扰。设置端板可阻止气流的展向流动,有效抑制端部效应。 (2)采用无量纲动压差乘以考虑距离因素的修正系数建立了端板尺寸估算模型,得到P0X和P0Y值,该值可用来评价断面周围任意位置展向流动对模型气动力的影响。 (3)由风洞试验和数值模拟结果得到模型宽度方向P0X=10,模型高度方向P0Y=15时,所得到的端板尺寸即可保证有效抑制端部效应。此值可作为标准来考虑以反算出二元端板的合理尺寸。 (4)估算模型中的部分假定有优化的空间,后续可将计算方法进行改进,例如提出有足够依据的修正系数模型得到更为精确的P0X和P0Y计算方法。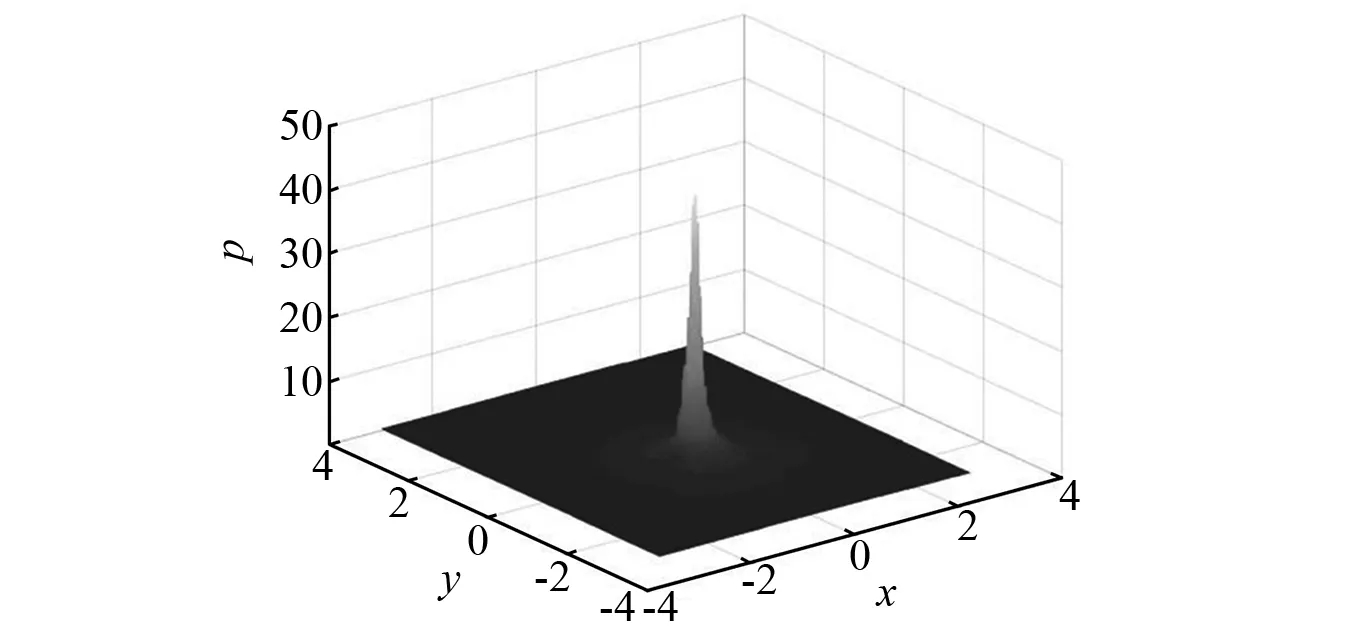
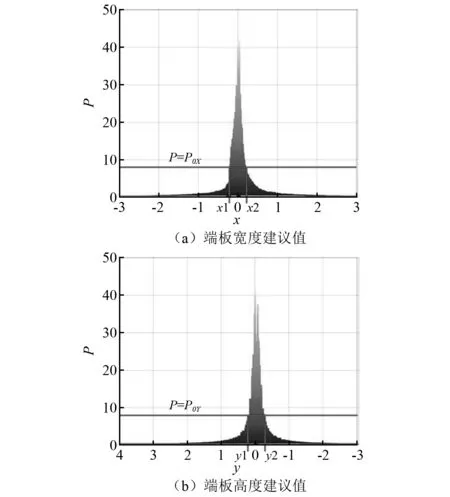
3 估算方法在风洞试验中的应用
3.1 风洞试验
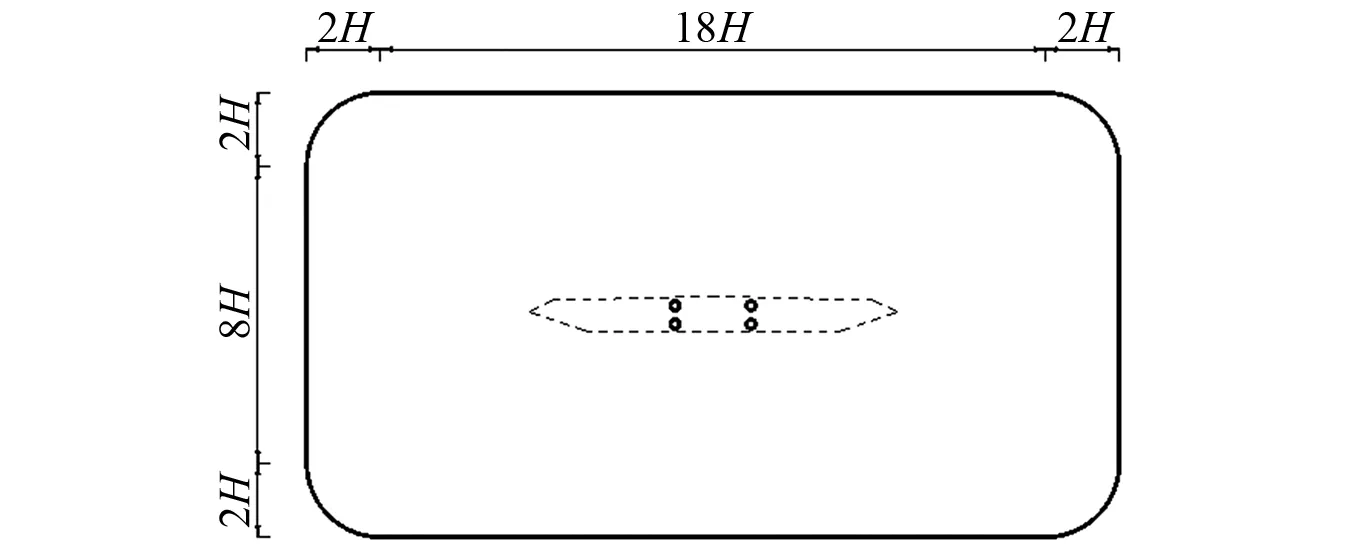


3.2 合理P值的确定
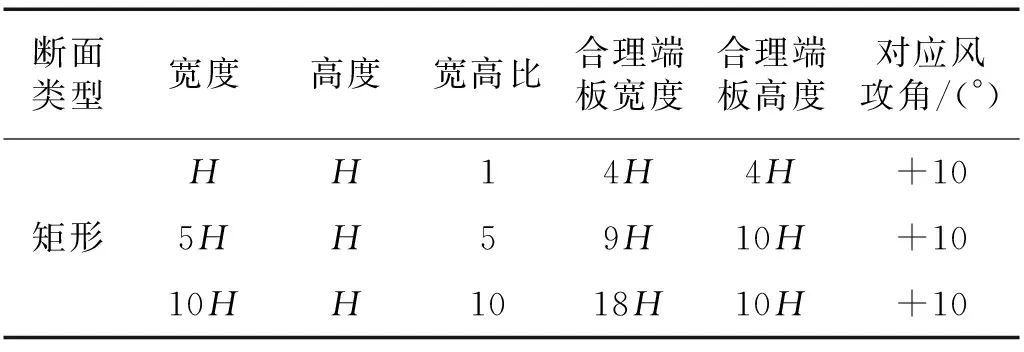




3.3 合理P值的检验


3.4 估算合理端板尺寸流程
4 结 论
