关于具有相对迷向平均Landsberg曲率的芬斯勒流形的一个刚性定理

程新跃，刘树华，殷 丽，李婷婷

(重庆理工大学 理学院， 重庆 400054)

关于具有相对迷向平均Landsberg曲率的芬斯勒流形的一个刚性定理

程新跃，刘树华，殷 丽，李婷婷

(重庆理工大学 理学院， 重庆 400054)

研究了闭的具有相对迷向Landsberg曲率(即J+c(x)FI=0)的芬斯勒流形，并证明了若c(x)在流形上恒为正或恒为负，则该流形一定是黎曼流形。

芬斯勒流形；黎曼流形；Landsberg曲率；平均Landsberg曲率

给定光滑流形M上的一个芬斯勒度量F,其基本张量g的定义为

其中

(1)

黎曼流形是特殊的芬斯勒流形。 对于芬斯勒流形(M,F),由基本张量的定义可知,若F所对应的基本张量g与y无关,则是黎曼流形。 为了区分芬斯勒度量中的黎曼度量，E.Cartan引入了Cartan张量C,

(2)

其中

(3)

Cartan张量C的平均值I称为平均Cartan张量，其定义为

(4)

其中gij=(gij)-1。

由式(2)、(3)可知：C=0等价于gij与y无关,即F为黎曼度量。进一步地,Deicke于1953年证明了如下定理：

Deicke定理[1]一个正定的芬斯勒度量是黎曼度量的充分必要条件是其(平均)Cartan张量等于零。

将平均Cartan张量I沿着测地线的变化率称为平均Landsberg曲率,记为J,其定义为

(5)

其中“|”表示在陈联络下关于F的水平协变导数。

若(M,F)满足条件J=0,则称(M,F)为弱Landsberg流形。更一般地,若存在流形M上的光滑函数c(x)使得J+c(x)FI=0成立,则称(M,F)为具有相对迷向平均Landsberg曲率的芬斯勒流形。 可以发现：许多重要的芬斯勒度量都具有相对迷向平均Landsberg曲率[2-4]。

在芬斯勒几何中,一个非常自然而重要的问题是：在怎样的几何条件下,芬斯勒流形一定是黎曼流形？

芬斯勒几何学家们就这一问题展开了大量的研究,并取得了较多成果。在负常数旗曲率的情形下,Akbar-Zadeh于1988年证明了任一闭的具有负常数旗曲率的芬斯勒流形一定是黎曼流形[5]。 在正常旗曲率的情形下,Kim和Yim于2003年证明了任一具有正常数旗曲率且S-曲率为0的可反芬斯勒流形一定是黎曼流形[6]。在非零常数旗曲率的情形下,沈忠民教授于2001年证明了任一具有非零常数旗曲率的弱Landsberg流形一定是黎曼流形[7]。在负旗曲率的情形下,沈忠民教授于2005年证明了任一闭的具有负旗曲率且具有常数S-曲率的芬斯勒流形一定是黎曼流形[8,9]。特别地,吴炳烨在2007年证明了任一闭的具有负旗曲率的弱Landsberg流形一定是黎曼流形[10]。

联系芬斯勒流形具有相对迷向平均Landsberg曲率的定义,对比文献[10]中的结论,自然地产生一个问题：在什么样的条件下,具有相对迷向平均Landsberg曲率的芬斯勒流形一定是黎曼流形？

本文针对这一问题展开了研究,并得到了如下定理：

定理1 设(M,F)是闭的具有相对迷向平均Landsberg曲率的芬斯勒流形,即J+c(x)FI=0。若其中的c(x)在流形M上恒为正或恒为负,则(M,F)一定是黎曼流形。

1 预备知识

令(M,F)是一个n维芬斯勒流形,记

是它的带孔切丛。自然丛投影π:TM0→M诱导了TM0上的向量丛π*TM(它是TM在自然的丛投影下的拉回切子丛),π*TM在一点 (x,y)∈TM0的纤维是

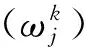
2) 与度量的几乎相容性：

(6)

这里,

(7)

对于n维芬斯勒流形(M,F),F的测地线可以由下述2阶微分方程组给出：

其中

Gi称为F的测地系数。

可以定义TM0上的光滑函数f:TM0→R关于陈联络的协变微分

(8)

其中：f|i为f的水平协变导数；f.i称为f的垂直协变导数。

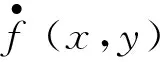
(9)

根据直接计算可知：

(10)

若流形M是闭的光滑流形,吴炳烨证明了如下的重要结论[10]：

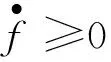
引理1将是以下证明主要定理的一个重要工具。

2 定理的证明

在证明定理1之前,首先证明如下定理：

定理2 设F是定义在闭流形M上的芬斯勒度量。 若F具有相对迷向平均Landsberg曲率(即J+c(x)FI=0),且在流形M上恒有c(x)≥0(或c(x)≤0),则(M,F)一定为下列情形之一：

1) 若c(x)=0,则(M,F)是弱Landsberg流形；

2) 若c(x)≠0,则(M,F)是黎曼流形。

2F2Ii|mymIjgij

(11)

将式(5)代入式(11)可得：

(12)

根据已知条件,有J+c(x)FI=0,即Ji+c(x)FIi=0。于是,可以将式(12)改写为：

(13)

若c(x)=0,则由J+c(x)FI=0有J=0,此时(M,F)一定是弱Landsberg流形。

若c(x)≠0,则有‖I‖=0,故I=0,根据Deicke定理可知(M,F)一定是黎曼流形。

定理2证明完毕。

接下来证明定理1。

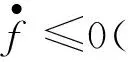
如前所述,吴炳烨证明了具有负旗曲率的闭的弱Landsberg流形一定是黎曼流形[10]。相比于这一结论,本文的定理1去掉了旗曲率的限制条件,并且将曲率条件“J=0”弱化为“J+c(x)FI=0”,却仍然得到了“(M,F)一定是黎曼流形”的同样的结果。

进一步地,结合上述吴炳烨的结论,可以得到如下推论：

推论1 设(M,F)是闭的具有相对迷向平均Landsberg曲率的芬斯勒流形,即J+c(x)FI=0， 若在流形M上恒有c(x)≥0(c(x)≤0),且F具有负旗曲率,则(M,F)一定是黎曼流形。

需要说明的是：定理1中的条件“(M,F)是闭的”芬斯勒流形不能去掉,否则定理就可能不成立.举例如下：

例1[3]令Ω是Rn中的一个有界开集,其边界∂Ω是严格凸的，则在Ω上可唯一定义一个度量F,满足

Fxk=FFyk

(14)

满足式(14)的度量称为Funk度量。 易证,F具有相对迷向平均Landsberg曲率J±(1/2)FI=0。

若∂Ω=Sn-1,容易验证Funk度量F为

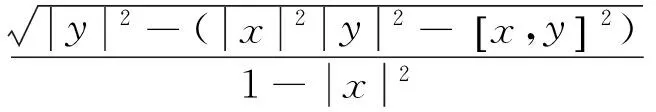
y∈TxRn

(15)

易见,由式(15)确定的Funk度量F定义在Rn中的一个有界开球Ω=Bn(1)上,且具有相对迷向的平均Landsberg曲率,其中c=±(1/2)在Ω上保持定号， 显然,此时F不是一个黎曼度量。

[1] DEICKE A.Uber die Finsler-Raume mitAi=0[J].Arch Math,1953,4:45-51.

[2] CHENG X,MO X,SHEN Z.On the flag curvature of finsler metrics of scalar curvature[J].Journal of the London Mathematical Society,2003,68(3):762-780.

[3] CHENG X,SHE N.Randers metrics with special curvature proper Zties[J].Osaka J Math,2003,40:87-101.

[4] CHENG X,SHEN Z.A class of Finsler metrics with isotropic S-curvature[J].Israel J Mathematics,2009,169(1):317-340.

[5] AKBAR-ZADEH H.Sur Les Espaces de Finsler A Courbures Sectionnelles[J].Acad Roy Belg Bull Cl Sci,1988,74(5):271-322.

[6] KIM C W,YIM J H.Finsler manifolds with positive constant flag curvature[J].Geom Dedicata,2003,98:47-56.

[7] SHEN Z.Lectures on Finsler Geometry[M].Singapore:World Sci,2001.

[8] SHEN Z.Nonpositively curved Finsler manifolds with constant S-curvature[J].Math Z,2005,249:625-639.

[9] SHEN Z.Volume comparison and its applications in Riemann-Finsler geometry[J].Advances in Mathematics,1997,128:306-328.

[10]WU B.A global rigidity theorem for weakly Landsberg manifold[J].Science in China,series A,2007,37(3):285-290.

[11]CHERN S S,SHEN Z.Riemannian-Finsler Geometry[M].Singapore:Worid Sci,2005.

(责任编辑 林 芳)

A Rigidity Theorems About Finsler Manifolds with Relatively Isotropic Mean Landsberg Curvature

CHENG Xinyue, LIU Shuhua, YIN Li, LI Tingting

(College of Science, Chongqing University of Technology, Chongqing 400054, China)

In this paper, we study the closed Finsler manifold of relatively isotropic mean Landsberg curvature withJ+c(x)FI=0. We prove that ifc(x) is always negative or positive on the manifold, then the Finsler manifold must be Riemannian manifold.

Finsler manifold; Riemannian manifold; Landsberg curvature; mean Landsberg curvature

2017-01-09 基金项目：国家自然科学基金资助项目(11371386)

程新跃(1958—)，男，重庆人，博士，教授，主要从事微分几何及其应用研究,E-mail:chengxy@cqut.edu.cn。

程新跃,刘树华,殷丽,等.关于具有相对迷向平均Landsberg曲率的芬斯勒流形的一个刚性定理[J].重庆理工大学学报(自然科学)，2017(8):170-173.

format：CHENG Xinyue, LIU Shuhua, YIN Li, et al.A Rigidity Theorems About Finsler Manifolds with Relatively Isotropic Mean Landsberg Curvature[J].Journal of Chongqing University of Technology(Natural Science)，2017(8):170-173.

10.3969/j.issn.1674-8425(z).2017.08.028

O186.13

A

1674-8425(2017)08-0170-04