目标函数带线性约束块可分的凸优化方法

曾 琴

(重庆师范大学 数学科学学院， 重庆 401331)

目标函数带线性约束块可分的凸优化方法

曾 琴

(重庆师范大学 数学科学学院， 重庆 401331)

带有线性约束条件且目标函数是块可分的凸性最小问题一直是研究的重点。该问题是经过研究目标函数由2个不是充分光滑的凸函数组成或是由3个不是充分光滑的凸函数组成，从而推广到目标函数由n个不是充分光滑的凸函数组成的情况。问题的解决是以经典的交替方向法为基础，延伸出多种方法来建立该模型。总结了几种常见方法,同时提出了新方法——基于分离法的新ADMM法，并证明该方法的可行性。

块可分；凸优化；线性约束条件；新ADMM法

本文研究的仅仅是一种带有线性约束条件且目标函数是块可分的凸性最小问题。该模型表明：在凸性假设和约束品性为线性条件的情况下，序列的每一个聚点才是它的最优解。本文主要总结常见的、较成熟的几种方法，并在此基础上提出新方法。文献[1]采用增广拉格朗日法，简称ALM，该方法具有不可分离的缺点，但其收敛速度和数值优势却提供了强有力的分离项，因此根据该优势可通过增加1个二次项，利用交替的线性技术来进行改进。另外，还可采用交替方向乘子法(ADMM)，但在该方法的迭代过程中为解决产生的子问题可能存在一些困难，故可针对此改进该方法。与交替方向乘子法(ADMM)类似的便是交替方向法(ADM)，它是由Peaceman和Mercier首次提出，由Glowinski和Marrocco进行发展。文献[2]采用线性近端的ADM法，其主要贡献在于简化子问题。目前有3种版本：第1种和第2种都是分别进行线性化二次项，增加邻近项；第3种版本是第1、2两种版本的结合，同时进行线性化二次项，增加邻近项。本文还介绍了高斯向后替换的线性ADM法。值得说明的是：尽管ADME法的数值性很好，但其收敛性还有待证明。其他方法如：ADBC法、ADM-based splitting method与ADME法类似，都要用校正步骤，而HTY法虽然无需校正步骤，但它需要一个更新的乘子λ。除了这些方法，还有加速分离的增广拉格朗日法(ADAL)、对偶法(dual methods)、对角二次逼近法(DQA)、交替步法(ASM)等。

1 预备知识

1.1 方法回顾

让Xi⊆Rni,i∈φ={1,2,…,N} 分别是ni维欧式空间中的非空闭凸子集，而θi:Rni→R,i∈φ是凸函数，是m×ni的矩阵，其中i=1,2,…,N.。本文所考虑的模型可用下式表示：

(1)

通过阅读大量的文献以及对资料的查找，对于式(1)这种带有线性约束条件、目标函数又是块可分的凸性最小问题，常见处理方法如下：解决这种模型的本质就是把带有约束条件的优化问题转换为无约束条件的优化问题，这样相当于解一个无约束条件的优化问题。解无约束条件优化问题的方法很多，如一致收缩法、对分法、黄金分割法、斐波拉切法、牛顿法等，这样问题(1)就得以解决。因此，现在问题是：怎样把带有约束条件的优化问题转换为无约束条件的优化问题？怎样解带有线性约束条件、目标函数又是块可分的凸性最小问题？

1.1.1 增广拉格朗日方法(ALM)

经典的增广拉格朗日方法(ALM)是通过引入1个拉格朗日乘子λ和1个罚参数β,将有约束条件的优化问题转换为无约束条件的优化问题，即将原问题从数学式转换为如下的代数形式：

(2)

其中：λ∈Rn是拉格朗日乘子；β>0是一个罚参数。该方法的迭代形式如下：

(3)

(4)

由于增广的拉格朗日法(ALM)破坏了xi的分离性，导致计算较复杂，但其收敛速度和数值优势却提供了强有力的分离项，因此利用该优势通过增加一个二次项，利用交替的线性技术做改进，有利于产生新思考和新方法。

1.1.2 交替方向乘子法(ADMM)

第2种是交替方向乘子法(ADMM)，具体迭代形式如下：

(5)

(7)

其中：λ∈Rn是拉格朗日乘子；β>0是罚参数。该方法必须先算出一个值，然后再算下一个值，不能并行计算(并行计算可减少计算时间，提高计算速度)。由于该方法在迭代中解决产生的子问题可能存在一些困难，可改进该方法以克服这个困难。与该方法类似的是交替方向法(ADM)。

1.1.3 交替方向法(ADM)

第3种是交替方向法(ADM)，其迭代形式如下：

(8)

(10)

从迭代式中可以看到：用交替方向法(ADM)计算模型(1)，经验上能起作用，但其收敛性在理论上目前还没有得到证明，因此可向该方向努力。那什么时候它的收敛性就能得到保证？研究表明：当所涉及的块可分的目标函数是强凸时，交替方向法(ADM)就是全局收敛的，这时其收敛性就能得到保证。

1.1.4 线性近端的ADM法

第4种是线性近端的ADM法。该方法引入了一个放缩因子，且该方法同ADM法以及近端的ADM法有相同的限制域。线性近端的ADM法是在ADMM法的基础上加以改进，思想最初源于ADMM法。迭代形式如下：

(11)

(12)

⋮

(13)

在解决其子问题时，线性近端的ADM法通常有3种处理方式，这3种处理方式的目的都是为了简化子问题，具体处理方式如下：

1) Algorithm1

第一种版本的线性近端点ADM法，具体步骤：

① 给出已知条件为：

(14)

(15)

⋮

(16)

③ 终止条件：若满足

(17)

则停止计算得到wk+1,此时wk+1就是该问题的最优解；否则k=k+1,回到第②步重新计算，直到满足终止条件为止。

2) Algorithm2

第2种版本的线性近端点ADM法，具体步骤如下：

① 给出已知条件为

(18)

(19)

⋮

(20)

③ 终止条件：若满足

(21)

则停止计算得到wk+1,此时wk+1就是该问题的最优解；否则k=k+1,回到第②步重新计算，直到满足终止条件为止。

3) Algorithm3

第3种版本的线性近端点ADM法，具体步骤如下：

① 给出已知条件为

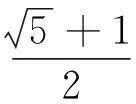
(22)

(23)

⋮

(24)

③ 终止条件：若满足

(25)

则停止计算得到wk+1,此时wk+1就是该问题的最优解；否则k=k+1,回到第②步重新计算，直到满足终止条件为止。

可以看出这3种处理方式的共同特点都是进行线性化二次项，增加邻近项。线性近端点的ADM法的收敛性和数值性都比较好，是一种较流行的方法。

1.1.5 高斯向后替换的线性ADM法

第5种方法见文献[3]，是高斯向后替换的线性ADM法。

让β>0,α∈(0,1)

(26)

(27)

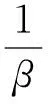
(28)

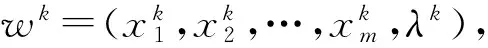
(29)

(30)

其中有：

(31)

② 高斯向后替换步(校正步骤)：

(32)

该方法的第②步至关重要，也可转换为如下形式：

(33)

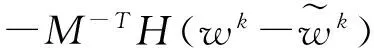
1.1.6 ADME法

第6种是ADME法。该方法是基于ADM法的思想，只是在迭代形式上有变化，其迭代形式为：

(34)

(35)

⋮

(36)

从其迭代式可以看出：虽然ADME法的数值性比较好，但其收敛性目前还没有得到证明，正因为如此，可以通过适当的校正步骤来校正ADME法的输出，从而产生新的迭代方法。在进行校正步骤时，根据其简易程度又可分为ADBC法与ADM-basedsplittingmethod法。

1.1.7ADBC法

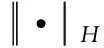
(37)

(38)

d(u,v)=M(u-v)

(39)

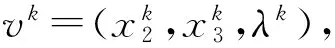
① ADM迭代步骤:

(40)

(41)

(42)

(43)

② 收缩步骤:

(44)

其中

*

(45)

(46)

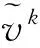
1.1.8ADM-basedsplittingmethod

第8种是ADM-basedsplittingmethod，以三维为例，具体步骤如下：

① 给出下面的已知条件为：

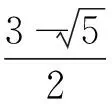
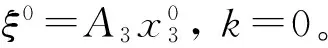
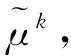
(47)

(48)

(49)

(50)

(51)

以上叙述的交替方向法(ADM)、ADM-based splitting method方法的全局收敛性能得到证明，且可以看到该方法在每次迭代时通过轻微的校正计算就能产生一个新的迭代，从而校正了交替方向法(ADM)的输出结果。由文献[5]知ADM-based splitting method也是一种很好的处理方法。

1.1.9 HTY法

第9种是HTY法，以三维为例，该方法不像第7种与第8种方法对校正步骤要求较严，即HTY法不需要校正步骤而是需要有一个更新的乘子。具体迭代步骤为：

其中η>2。

1.2 变分不等式

让W=X1×X2×…×Xm×Rl,对问题(1)而言，通常是在它的最优性条件下,将问题(1)等价转换，目的是找一个满足下列不等式的点w*,见文献[6-7]，具体的不等式为：

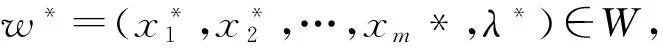
VI(W,F,θ):θ(x)-θ(x*)+(w-w*)TF(w*)≥0, ∀w∈W,

通过对以上9种方法的叙述以及对变分不等式的回顾，可知处理问题(1)还有其他的方法，这里不再一一叙述。通过对这些经典方法的回顾，本文在第2部分提出基于分离法的新ADMM法。

2 基于分离法的新ADMM法

在交替方向法(ADM)、ADBC法以及通常的ADMM法的基础上，本文描述了一种新的ADMM法。该方在文献[8]的启发下，可以看到在每次迭代中，新方法通过轻微的校正计算就能产生一个新的迭代，以三维为例。

minθ1(x1)+θ2(x2)+θ3(x3)

s.tA1x1+A2x2+A3x3=b

x1∈X1,x2∈X2,x3∈X3

具体迭代步骤如下：

① 初始点的选择：

(52)

④ 收敛准则(终止条件)：

(53)

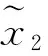
3 结束语

本文研究了一种带线性约束条件且目标函数是块可分的凸性最小问题，即形如问题(1)。该问题一般需要用变量分离的方法来解决。对于式(1)这样的问题，建议充分利用问题本身的结构，如问题(1)具有很好的分离性，然后结合研究产生新ADMM法。从本文的研究结果可以看出：基于分离法的新ADMM法的校正步骤比较简单，减少了计算量，输出结果效果较好。总的来说，新方法表明这种分离方法具有吸引性和可行性。

[1] CHATZIPANAGIOTIS N,DENTCHEVA D,ZAVLANOS M M.An augmented lagrangian method for distributed optimization[J].Mathematical Programming,2015,152(1/2):405.

[2] XU M H,WU T.A class of linearized proximal alternating direction methods[J].Optim Theory Appl,2011(151):321-337.

[3] HE BH,TAO M,YUAN X M.Alternating direction method with gaussian back substitution for separable convex programming.SIAM[J].Optim,2012(22):313-340.

[4] HE B,YUAN X.Linearized alternating direction method with gaussian back substitution for separable convex programming[J].Numerical Algebra,Control and Optimization,2013,3(2):247-260.

[5] HE B,XU M,Yuan X.Solving large-scale least squares semidefinite programming by alternating direction methods[J].SIAM Journal on Matrix Analysis and Applications,2011,32(1):136-152.

[6] TAO M,YUAN X.On theO(1/t) convergence rate of alternating direction method with logarithmic-quadratic proximal regularization[J].SIAM Journal on optimization,2012,22(4):1431-1448.

[7] HE B S,TAO M,YUAN XM.A splitting method for separable convex programming[J].IMA Journal of Numerical Analysis,2015(35):394-426.

[8] HAN D,KONG W W,ZHANG W X.A partial splitting augmented lagrangian method for low patch-rank image decomposition[J].Math Imaging Vis,2015,(51):145-160.

(责任编辑 刘 舸)

Summary of the Method of Convex Optimization Problem on the Objective Function with the Linear Constraints Block Divided

ZENG Qin

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

The convexity minimum problem with a linear constraints and a block separable objective function is always studied. As you can see from this article, the objective function which is composed of two or three insufficiently smooth convex functions is firstly studied to promote the objective function composed ofninsufficientlysmoothconvexfunctions.Thesolutiontothemodelisbasedontheclassicalternatingdirectionmethod.Therefore,itstretchesoutalotofkindsofmethodstosolvethemodel.Thearticlesummarizesthecommonmethods,andthenitputsforwardanewmethod:anewADMMmethodbasedonseparationprocess,anditsimultaneouslyindicatesthemethod’sfeasibility.

block of dividing；convex optimization； linear constraint condition;a new method of ADMM

2016-11-09 基金项目：国家自然科学基金资助项目(11501070)；重庆市自然科学基金资助项目(cstc2015jcyjA00011)

曾琴(1991—)，女，重庆人，硕士研究生，主要从事运筹学理论和算法研究，E-mail:823235519@qq.com。

曾琴.目标函数带线性约束块可分的凸优化方法[J].重庆理工大学学报(自然科学)，2017(8):182-191.

format：ZENG Qin.Summary of the Method of Convex Optimization Problem on the Objective Function with the Linear Constraints Block Divided[J].Journal of Chongqing University of Technology(Natural Science)，2017(8):182-191.

10.3969/j.issn.1674-8425(z).2017.08.030

O224

A

1674-8425(2017)08-0182-10