基于双谱的汽油机爆震特征提取与强度评价*
2017-09-12刘昌文毕凤荣毕晓博
张 剑,刘昌文,毕凤荣,毕晓博
(天津大学内燃机燃烧学国家重点实验室 天津,300072)
基于双谱的汽油机爆震特征提取与强度评价*
张 剑,刘昌文,毕凤荣,毕晓博
(天津大学内燃机燃烧学国家重点实验室 天津,300072)
将双谱分析应用于爆震振动信号分析,提出了爆震特征频率提取和强度判定的方法。首先,用功率谱密度估计的方法分析发动机3个方向的振动信号,确定爆震特征频率范围;然后,利用双谱分析不同爆震强度下的振动信号并提取双谱主对角线切片,分析不同状况下的信号频率间的相位耦合关系,确定爆震特征频率;最后,提出了爆震强度评价参数。试验结果表明,相比功率谱密度估计,双谱峰值频率更能凸显爆震特征频率,爆震强度评价参数能有效判定爆震强度。
振动信号; 爆震频率; 爆震强度; 双谱
引 言
以增压和直喷为代表的小型强化技术是提高汽油机热效率的重要技术途径[1]。研究表明,在当前技术水平下,根据不同的强化程度,小型强化技术可以带来15%~30%的油耗降低效果。但是,随着小型强化程度的提高,汽油机发生爆震的几率增加,剧烈爆震致使汽油机动力性、经济性下降,甚至损坏汽油机,但轻微爆震反而能改善汽油机的动力性和效率[2],因此及时有效地检测爆震并判定其强度具有重要的理论意义和工程实用价值。
目前,常用的爆震检测方法主要为直接检测法和间接检测法。前者主要基于燃烧压力[3]和离子电流[4]等,爆震状态识别精度高,但受传感器可靠性、发动机结构和成本限制,难以大范围推广应用[5]。检测缸体振动信号[6]属于间接方法,具有易安装、可靠性高以及成本低的优点。因此,基于振动信号的爆震检测已成为当前国内外研究的重要方向。
发动机缸体振动信号包含大量噪声,低信噪比增加了爆震检测和强度评价的难度,尤其是爆震边缘检测。国内外学者采用滤波、统计量以及时频分析等方法进行爆震特征提取和强度评价[7-10]。目前,基于傅里叶变换和数字滤波的滤波方法广泛应用于爆震检测,但在微弱爆震和信噪比较低的情况下难以识别。时频分析方法通过时频变换对比不同时频窗中的信号特征来判别爆震,易受噪声影响,同时爆震窗口的选取也会影响爆震判定结果。爆震发生时,末端混合气急剧燃烧,能量迅速释放,在燃烧室内形成高频压力振荡波,压力波不断冲击发动机缸壁,引起其被动振动并产生明显的金属敲击声。这种高频压力振荡波的传播具有方向性,以往的研究仅针对某一方向的振动信号进行分析,没有考虑其余方向的振动特性。双谱可以抑制信号中的高斯成分,又能分析信号频率成分间的相位耦合关系,广泛应用于机械故障振动诊断领域[11]。
笔者将双谱理论应用于爆震振动信号特性分析,通过一系列实际信号分析证明了方法的可行性及有效性。首先,用功率谱密度估计的方法分析发动机3个方向的振动信号,预估爆震特征频率;然后,利用双谱分析不同爆震强度下的振动信号,通过对双谱进行降维,从其主对角线切片中提取爆震特征频率;最后,根据爆震特征频率,提出了爆震强度评价参数KI的计算方法。
1 双谱分析
1.1 双谱定义
对于循环平稳过程的振动信号X(n),定义其双谱为
(1)

1.2 双谱的计算
对信号进行双谱计算时,参数化双谱估计可以在数据较短的情况下提供较高分辨率和信号的相位信息,计算量相对较小,但数据太短,不能全面反映信号特性,甚至丢失重要的特征信息。非参数化双谱估计通常用到相对较多的数据样本,可以减少估计方差、提高准确性,但计算量增大。为尽量反映出信号的重要特征,笔者采用非参数化双谱估计,其计算步骤[12]如下。
1) 将试验数据均分为K段观测数据,并对每段观测数据去除本段均值。
2) 计算各段数据的离散傅里叶变化系数
(2)
3) 根据式(2)结果计算三重相关
(3)
4) 计算平均值,得到双谱估计为
(4)

1.3 双谱切片

2 汽油机爆震试验
爆震试验在一台缸内直喷、涡轮增压四缸汽油发动机上进行。试验工况:转速为1 500~2 700 r/min,扭矩为200 Nm。试验时,在发动机四缸缸体顶部布置三向振动加速度传感器,同时布置AVL压力传感器测取四缸缸内压力信号。振动和缸压信号经LMS Scada声振测试系统以51.2 kHz的采样频率采集存储。在信号采集过程中,通过调整点火提前角来控制爆震的发生。图1(a)为转速1 500 r/min,在点火提前角为16.59°时测定的某一循环的缸压信号,通过缸压信号上的锯齿波可以判断出该循环产生了明显爆震。图1(b)为点火提前角为10.26°(正常燃烧状况)时测定的缸压信号。

图1 爆震发生与正常燃烧时的缸压信号Fig.1 Cylinder pressure signals under different knock conditions
图2为点火提前角为16.59°时对应的机体振动信号。发动机振动方向的定义如下:相对于发动机曲轴轴线,x向为曲轴轴向,y向为垂直曲轴水平横向,z向为垂直向。图3为点火提前角为10.26°时对应的机体振动信号。图2和图3 中每一个信号样本均包括4 096个采样点。

图2 爆震发生时的振动信号Fig.2 The vibration signals of knock on different direction
从图2可以看出,发生爆震时3个方向的振动加速度信号均有明显的冲击成分,且该成分和缸压信号出现锯齿波的时刻一致,但冲击成分的峰值各有不同,其中y向振动信号的峰值明显大于其余方向的振动信号,x向的峰值最小。这是因为y向处在缸内压力振荡和活塞敲击共同作用下,冲击能量很大;z向则受缸内压力振荡和气门落座冲击等因素影响,冲击能量较大;x向仅受缸内压力作用,所受冲击能量较小,幅值峰值最小。

图3 正常燃烧时的振动信号Fig.3 The vibration signals of non-knock in different direction
从图3可以看出,正常燃烧时3个方向的振动加速度信号均无明显的冲击成分,y,z向的幅值峰值比较接近,y向稍大,但两者均大于x向的幅值峰值,这和爆震发生时的规律一致,但相对于爆震时3个方向振动信号峰值的相对值远远减小。
3 爆震特征提取及强度评价
3.1 爆震特征频率范围的确立
爆震特征频率是爆震激励的机体振动响应的主要频率带。对机体振动信号进行功率谱密度估计并对比分析,如图4所示。可以看出,无论爆震与否,在5 kHz以下3个方向的功率谱基本重合,说明爆震频率在5 kHz以上,这和以往研究学者提出的爆震通常出现的5 kHz~25 kHz频带内[3,14]一致。有爆震发生时,x向的振动信号在5 950,7 150,9 633,12 940,16 650,18 580及21 780 Hz 7个特征频率上相比无爆震时存在明显峰值。y向的振动信号在7 500,12 850,17 400及21 500 Hz 4个特征频率上相比无爆震时存在明显峰值。z向的振动信号在7 050,12 900,17 650及21 350 Hz 4个特征频率上相比无爆震时存在明显峰值。x向特征频率较多是由于受活塞拍击和气门落座冲击影响较弱,而受缸内压力振荡影响较大,更能体现缸内压力变换情况。y向受活塞拍击和缸内压力振荡的双重作用。z向受气门落座冲击和缸内压力振荡影响,相比无爆震出现明显峰值的特征频率较少。进一步分析发现,y,z向的4个特征频率比较接近,x向也有4个特征频率与y,z接近,说明这4个特征频率为爆震特有频率。
3.2 爆震特征提取
由功率谱密度估计确定爆震特征频率的方法易受噪声影响,在信噪比较低和轻微爆震情况下很难区分。图5为无爆震和点火提前角为11.75°(微弱爆震)时,y向振动信号的功率谱密度估计谱图。可以看出,两者相比没有明显峰值,爆震频率难于提取。
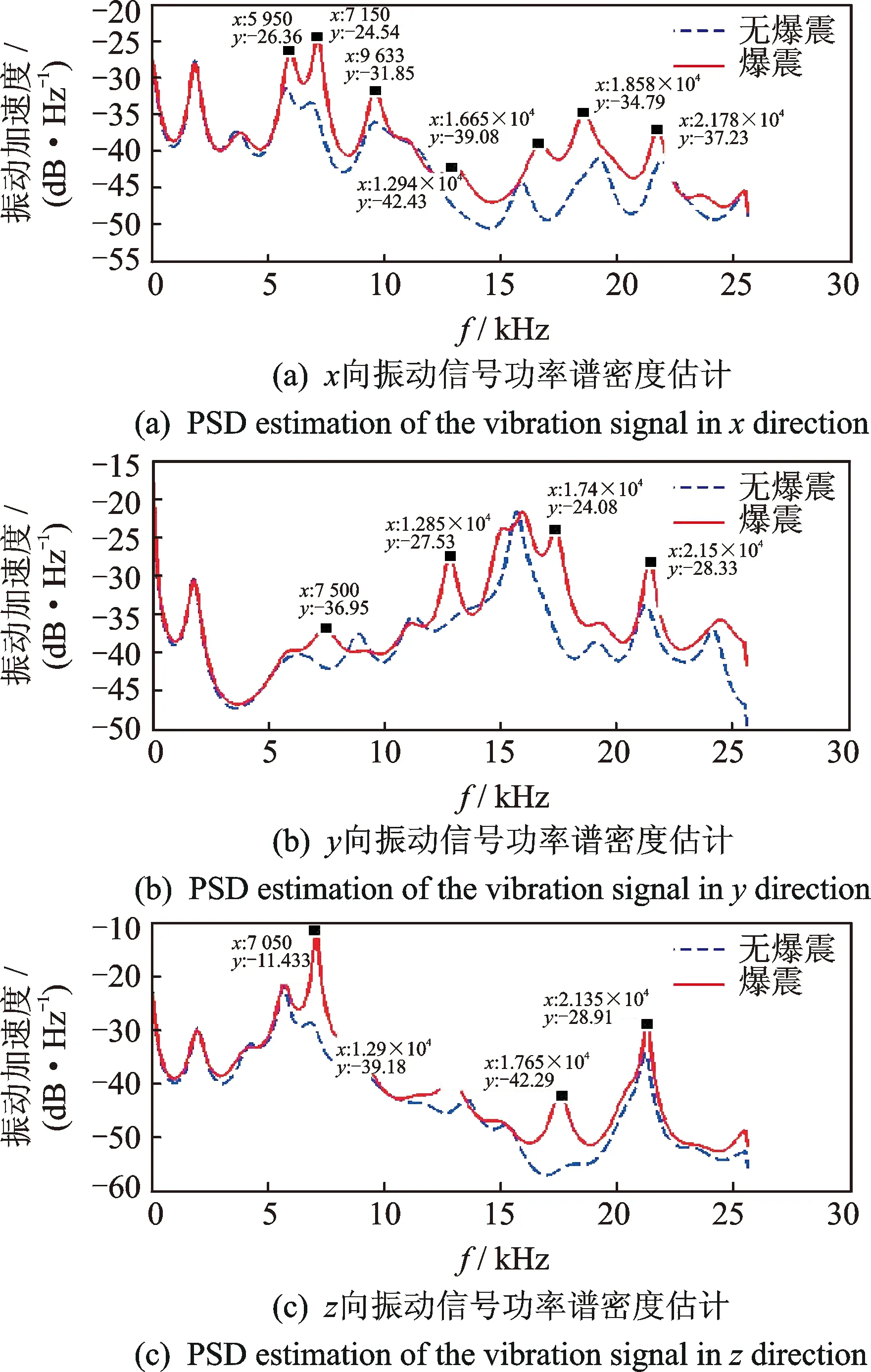
图4 无爆震与剧烈爆震下机体振动信号的功率谱密度估计Fig.4 The PSD estimation of vibration signals on different direction

图5 无爆震与轻微爆震下y向振动信号的功率谱密度估计Fig.5 The PSD estimation of vibration signals on y direction for non-knock and light-konck
信号分析时,相比相关函数和功率谱等二阶统计量,高阶累积量包含了更为丰富的信息,可以描述信号非线性、非高斯性特征,能够刻画频率间的二次相位耦合特征。爆震信号为非平稳信号,但在发动机完成一个工作循环内的爆震信号,其高阶统计特性是有规律可循的。双谱是高阶统计量理论中阶数最低、应用最广的高阶谱,具有高阶累积量的所有特点。利用非参数双谱估计爆震振动信号,数据分段长度为256,每段数据之间的重叠度为50%,共分为15段。图6为无爆震、轻微爆震和剧烈爆震下x向振动信号的双谱图。其中,f1,f2以双频的最大频率值为基准进行归一化处理,频率f1,f2(0~0.5 Hz)实际对应0~25.6 kHz,文中提到的频率均为归一化后的值。

图6 无爆震、轻微爆震和剧烈爆震下x向振动信号双谱图Fig.6 Bispectrum of vibration signal on x direction in different intensity knock conditions
从图6可以看出,随着爆震强度的增加,双谱幅度峰值逐渐突出,其相对应的频率也逐渐增大,幅度整体图形呈现由中心向周围扩散的趋势。无爆震时双谱峰值出现在(0.039 1,0.039 1)频率(实际为2 kHz)附近;微弱爆震时双谱峰值出现在(0.136 7,0.078 1)和(0.078 1,0.136 7)频率(实际为7 kHz)附近;剧烈爆震时双谱峰值出现在(0.136 7,0.078 1)和(0.078 1,0.136 7)频率(实际为7 kHz)附近。微弱爆震和剧烈爆震时的双谱峰值频率一致,说明该频率为爆震特征频率。同理,分析y,z向振动信号也得到相似的结果。
双谱是一个二维量,对其直接进行分析处理比较复杂,可以采用一维切片进行数据降维和爆震特征选择。通过大量试验分析后,选取双谱主对角切片作为特征进行分析。图7为无爆震、轻微爆震和剧烈爆震下振动信号的双谱切片。

图7 无爆震、轻微爆震和剧烈爆震下振动信号双谱切片Fig.7 Bispectrum slice of vibration signal in different intensity knock conditions
从图7(a)可以看出,在0.125~0.168 Hz(实际为6 400~8 600 Hz),0.414 1~0.445 3 Hz(实际为21 200~22 800 Hz)频率范围内,轻微爆震和剧烈爆震相比无爆震均出现明显峰值,故这两个频带范围为该振动方向的爆震特征频率。幅值峰值在0.136 7 Hz频率处(实际为7 kHz),由双谱的对称性可知,该峰值频率和双谱图中的爆震频率(0.136 7,0.078 1)和(0.078 1,0.136 7))相一致。从图7(b)可以看出,爆震特征频率集中在0.234 4~0.265 6 Hz(实际为12 kHz~13.6 kHz),0.277 3~0.296 9 Hz(实际为14.2 kHz~15 kHz),0.316 4~0.359 4 Hz(实际为16.2 kHz~18.4 kHz)频率范围内,峰值在0.339 8 Hz频率处(实际为17.4 kHz)。从图7(c)可以看出,爆震特征频率集中在0.062 5~0.078 1 Hz(实际为3.2 kHz~4 kHz),0.117 2~0.156 3 Hz(实际为6 kHz~8 kHz)以及0.406 3~0.437 5 Hz(实际为20.8 kHz ~22.4 kHz)3个频带范围内,峰值频率分别为0.070 3 Hz(实际为3.6 kHz),0.140 6 Hz(实际为7.2 kHz),0.418 Hz(实际为21.4 kHz)。和功率谱密度估计相比,双谱主对角切片更能凸显爆震特征频率。通过对处在爆震特征频率范围内的信号深入分析可对爆震强度进行评价。
3.3 爆震强度评价
由图7可以看出,处在爆震特征频率范围内的不同强度爆震的振动信号双谱切片的幅值有明显区分。据此,笔者提出单一振动方向的爆震强度评价指标k为

(5)
其中:N为爆震频率范围内的数据点数;x(i)为第i个数据点幅值;M为非爆震区域内的数据点数;y(j)为第j个数据点幅值。
经式(5)得到3个振动方向的爆震强度指标kx,ky,kz后,由式(6)得到总的爆震强度指标KI为

(6)
利用笔者提出的方法对无爆震、轻微爆震和剧烈爆震的振动信号进行爆震强度评价参数计算,结果如表1所示。为更加准确评价爆震强度,分析了发动机在不同转速下的振动信号,结果如图8所示。

表1 不同爆震强度工作循环的爆震评价参数Tab.1 Knock intensity evaluation parameters in different work cycles
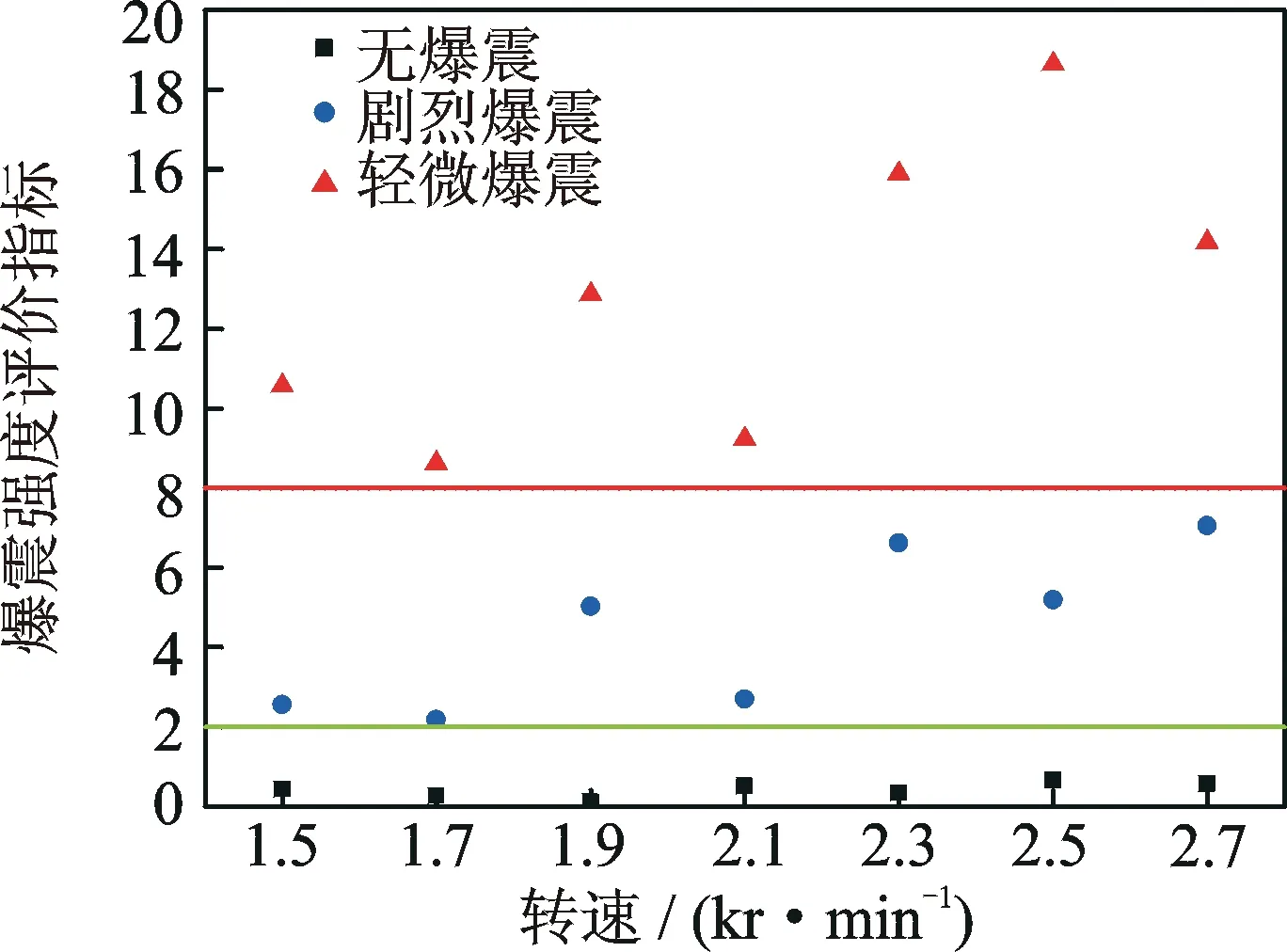
图8 不同转速爆震强度的评价参数计算结果Fig.8 Results of the knock intensity evaluation parameter calculation under different speed
可以看出,在3种爆震强度下,爆震强度评价参数KI有明显的差异且分布在不同的区域内。据此,界定无爆震KI的值在2以下;超过2时可以判断为轻微爆震的发生;当KI值超过8时,表明爆震强度较强,发生剧烈爆震。
4 结束语
双谱反映了爆震频率间的相位耦合特征,相比功率谱密度估计,双谱峰值频率更能凸显爆震的特征频率。基于双谱对角切片提出的爆震强度评价方法能够有效地区分不同强度的爆震。
[1] Lumsden G,OudeNijeweme D,Fraser N,et al.Development of a turbocharged direct injection downsizing demonstrator engine[J].SAE International Journal of Engines,2009,2(1):1420-1432.
[2] 韩璞,毕凤荣,张剑.基于振动的汽油机爆震始点识别与强度评价研究[J].内燃机工程,2016,37(5):134-139.
Han Pu,Bi Fengrong,Zhang Jian.Research on gasoline knock onset identification and knock intensity evaluation using vibration signal[J].Chinese Internal Combustion Engine Engineering,2016,37(5):134-139.(in Chinese)
[3] Hudson C,Gao X,Stone R.Knock measurement for fuel evaluation in spark ignition engines[J].Fuel Journal,2001,80:395-407.
[4] Wang Ying,Zhou Longbau.Investigation of the detection of knock and misfire of a spark ignition engine with the ionic current method[J].Journal of Automobile Engineering,2003,217(7):617-621.
[5] Boubai O.Knock detection in automobile engines[J].IEEE Transactions on Instrumentation and Measurement,2000,3(3):24-28.
[6] Ettefagh M M,Sadeghi M H,Rezaee M.Application of a new parametric model-based filter to knock intensity measurement[J].Measurement,2010,43(3):353-362.
[7] Lee J H,Hwang S H,Lim J S,et al.A new knock-detection method using cylinder pressure,block vibration and sound pressure signals from a SI engine[C]∥International Spring Fuels and Lubricants Meeting and Exposition.Michigan:[s.n.],1998.
[8] Wu Gang.A real time statistical method for engine knock detection[C]∥ SAE Technical Paper Series.Detroit:[s.n.],2007.
[9] Vulli S,Dunne J F,Potenza R,et al.Time-frequency analysis of single-point engine-block vibration measurement for multiple excitation-event identifica-tion[J].Journal of Sound and Vibration,2009,321:1129-1143.
[10]Li Ning,Yang Jianguo,Zhou Rui,et al.Knock detection in spark ignition engines using a nonlinear wavelet transform of the engine cylinder head vibration signal[J].Measurement Science and Technology,2014,25(11):115002.
[11]Shen Guoji,McLaughlin S,Xu Yongcheng,et al.Theoretical and experimental analysis of bispectrum of vibration signals for fault diagnosis of gears [J].Mechanical Systems and Signal Processing,2014,43:76-89.
[12]赵慧敏,夏超英,肖云魁,等.柴油发动机曲轴轴承振动信号的双谱分析[J].振动、测试与诊断,2009,29(1):14-18.
Zhao Huimin,Xia Chaoying,Xiao Yunkui,et al.Bispectrum analysis for vibration data of crankshaft bearing in diesel engine[J].Journal of Vibration,Measurement &Diagnosis,2009,29 (1):14-18.(in Chinese)
[13]Liang B,Iwnicki S D,Zhao Y.Application of power spectrum,cepstrum,higher order spectrum and neural network analyses for induction motor fault diagnosis [J].Mechanical Systems and Signal Processing,2013,39:342-360.
[14]段向阳,王永生,苏永生.切片双谱分析在离心泵故障诊断中的应用[J].振动、测试与诊断,2010,30(5):581-584.
Duan Xiangyang,Wang Yongsheng,Su Yongsheng.Application of slice bispectrum analysis to fault diagnosis of centrifugal pump[J].Journal of Vibration,Measurement &Diagnosis,2010,30(5):581-584.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.04.013
* 国家科技支撑计划资助项目(2015BAF07B04)
2015-09-22;
2015-12-28
TK417+.1
张剑,男,1983年11月生,博士生。主要研究方向为内燃机振动控制及状态检测。曾发表《柴油机气门故障信号的双谱图形分形维数分析》(《内燃机学报》2016 年第3期)等论文。 E-mail:neil1101@tju.edu.cn
