复杂系统相关失效分析研究综述

李志强，徐廷学，顾钧元，刘玉东

(1.海军航空工程学院 兵器科学与技术系，山东 烟台 264001；2.解放军95080部队，广东 汕头 515000)

复杂系统相关失效分析研究综述

李志强1，徐廷学1，顾钧元1，刘玉东2

(1.海军航空工程学院 兵器科学与技术系，山东 烟台 264001；2.解放军95080部队，广东 汕头 515000)

随着系统朝着复杂化、结构化、层次化方向发展，传统的可靠性评估与分析方法相互独立假设和二元状态假设的不足与缺陷逐渐显现出来。在设有冗余组件的复杂系统可靠性评估与分析中，相关失效分析的地位与作用越来越凸显。在引入相关失效定义与分类的基础上，对共因失效事件进行定义，并对传统故障树进行扩展。纵观相关失效的发展历程，归纳相关失效分析中5种常用方法的优缺点，包括β因子模型、基本参数模型、多希腊字母模型、α因子模型、二项失效率模型，预测今后复杂系统相关失效分析的研究方向，即不确定条件下的相关失效分析和多状态条件下的相关失效分析。

可靠性评估；相关失效；共因失效；不确定条件

0 引言

传统的可靠性评估与分析基于如下两个假设：

1)独立性假设，即假设复杂系统中各个元件之间的失效事件相互独立。

随着装备朝着复杂化、精密化、集成化等方向发展，为了保证大型装设备的有效工作时间，减少不必要的停机时间，一般采用冗余设计以获得更高的可靠度，即只有当系统中所有元件或者一定数量的元件发生失效时，系统发生失效。在实际工作中不难发现，冗余系统的失效概率普遍高于相互独立假设条件下的评估值，甚至在个别情况下，冗余系统的失效概率相比于传统方法评估值大几乎2个或者更多个数量级[1-2]。这正好说明了传统的系统可靠性分析方法已经无法全面地反映一个或多个起支配作用的系统故障原因。

2)二态性假设，即假设复杂系统中各个元件只有正常运行和故障停工两种状态。

传统的可靠性研究主要集中于只考虑元件或者系统正常运行与故障停工两种状态[3]，即系统从正常运行到故障停工采取“突变”模式。这种模式对于部分电子元器件或者精密仪器适用，但现实世界中的很多系统都是由具有不同性能参数和多种故障模式的元件组成。根据不同的判定准则，二元可靠性模型将这些元件的技术状态划为正常或者故障，造成了大量的信息遗失，进而影响了可靠性分析的正确性。近年来，随着基于Markov模型、贝叶斯理论模型的复杂系统多状态理论的发展，“渐变”理论的引入充分表征了处于正常运行与故障失效之间的若干中间状态，为复杂系统的可靠性评估与分析提供了新思路和新方法。

工程实践中，复杂系统的失效率普遍高于基于相互独立假设条件下的评估值，甚至相差甚远。造成这一差异的根源在于复杂系统子系统之间或元件之间因为位置空间、环境条件、结构设计以及人的因素等使得复杂系统的失效事件不再是独立事件，而可能因为某种情况造成多个元件同时或者接近同时发生故障或失效，以致于复杂系统发生故障或失效，即相关失效(Dependent Failure)。

“相关”作为复杂系统的普遍特征，因此，在复杂系统中，每个元件在一定程度上是相关的。如果忽略了复杂系统中各个元件失效事件之间的相关性，仅仅把各个元件的失效事件当作相互独立的事件，在进行可靠性评估与分析时，往往会造成较大的误差，从而增加了装备维修保障的费用，以及由于故障停机带来的损失。这正好解释了为什么相关失效使得复杂系统可靠性降低以及传统独立性假设为什么在复杂系统中不再适用。

1 相关失效定义

1.1 相关失效的定义与分类

以二元件系统为例，设表示元件处于失效状态，则2个元件均失效的概率为

(1)

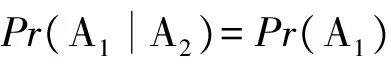
(2)

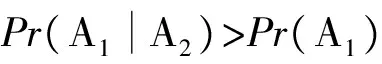
(3)

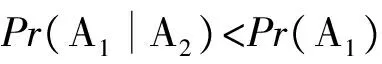
(4)

当前，对于相关失效还没有一个统一的定义，但大致可以这样描述：出于位置空间、环境条件、结构设计以及人因失效等原因，复杂系统中原有各个元件的失效事件不再是独立失效事件，而存在着相互作用、相互依存的关系。在工程实践中，相关失效主要分为如下3种形式：

1)级联失效。在级联失效系统中，某个元件的失效引起整个系统的操作条件、使用环境或负荷分配等要素发生改变，从而引起其它元件相继发生失效，也称为传播失效或者因果失效。如在由2个相同元件组成的并联系统中，某一元件的失效，增加了另一元件的负载，恶化了工作环境，从而缩短了这一元件的剩余工作寿命。

2)负相关失效。负相关失效[4]，即复杂系统中某个元件的失效降低了其他元件失效的概率，典型的负相关失效事件为互斥事件失效。

3)共因失效。在某一种共同原因的作用下，复杂系统中2个或2个以上的元件在同一时间或相隔很短的时间段内发生失效或故障[5-7]。在复杂系统共因失效分析中，系统与各个元件的失效不再是独立失效事件，各个元件之间的相关性使得复杂系统中2个或2个以上元件同时或者几乎同时发生失效。

通常情况下，共因失效由5种原因造成：1)设计上的缺陷，包括系统内在设计上的缺陷和系统之间设计上的缺陷；2)生产制造和加工工艺等方面的缺陷，如材料不纯、工艺不精、制造设备不完善等；3)包装、存储、运输、安装等方面的缺陷；4)操作人员的错误，如不当的操作、数据读取与记录错误、个人不良习惯下的校对、检查等；5)共同环境因素的影响，包括正常环境和异常环境(如地震、火灾、洪水等自然灾害)。正常环境条件下发生的失效事件属于随机事件，而在异常环境条件下所有元件都将发生失效。共因失效广泛存在于各种复杂系统中，尤其是核工业系统、大型电力系统、机械系统、计算机网络系统，由于其对冗余系统可靠性评价的影响，成为了众多领域技术人员的研究重点，这也是本文分析的重点。

1.2 共因基本事件的定义

共因基本事件[5,8]，即一个共因元件组中可以代表几个特定元件失效的基本事件。在一个由3个相同元件A、B、C构成的2/3表决系统中，在条件独立的情况下，系统的最小割集为：{A，B}、{A，C}、{B，C}，系统失效的布尔运算表达式为

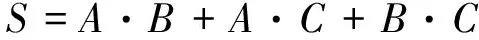
(5)

如果考虑共因失效事件，则元件A的失效事件可以表示为

(6)

式中：AT为元件A完全失效；AI为元件A独立失效；CAB为元件A和B同时失效而C不失效；CABC为元件A和C同时失效而B不失效；为元件A、B、C同时失效。

应用此方法将元件B和C失效事件进行展开，可以建立如图1所示的扩展故障树。

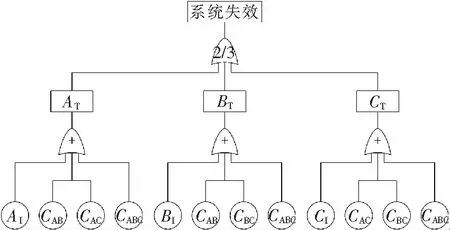
图1 相关失效条件下的扩展故障树Fig.1 Extended fault tree considering dependent failures

系统的最小割集为

系统失效的布尔运算表达式为

S=A1·B1+A1·C1+B1·C1+

(7)

在已知各个基本事件故障率的情况下，系统的失效率为

(8)

假设3个元件具有相同的故障率，即

则，式(8)可以简化为

(9)

系统的失效率可以通过Q1、Q2和Q3的值确定。对于由m个元件组成的共因元件组，基本事件的发生概率可以作出如下定义：

Qk=包括k个特定元件的基本事件的故障率，1≤k≤m。

可见，系统失效率QS是Qk的函数，只要知道Qk就可以确定系统的失效率，因此，共因失效定量分析的落脚点即确定Qk。

元件的失效概率式(6)可以写成：

(10)

式中，Qt表示元件的总失效概率。

对于含有m个元件的共因元件组，元件的失效率可以表示为

(11)

2 相关失效研究的发展

在20世纪50、60年代，在核工业反应堆设计与运行阶段的可靠性分析中，出现了相关失效分析的雏形，当时称之为“系统失效(Systematic Failure)”、“交叉耦合故障(Cross-linked Faults)”。1968年美国原子能委员会将之命为“共模失效(Common Mode Failure, CMF)”，此后，Epler发表了关于相关失效的文章，引起了核工业界众多研究人员的重视，并于70年代中期出现了共因失效的重要概念。在往后的将近40年时间里，相关失效分析得到了快速发展，其发展历程如图2所示。相关失效分析伴随着β因子模型、基本参数模型、多希腊字母模型、α因子模型、二项失效率模型等基本模型的提出与改进而迅速发展，并广泛应用于核工业、航天航空、大型机械部门的概率风险分析中。应力-载荷模型的提出将应用领域拓展到了机械强度分析中。原因分析与防御矩阵的建立为预防与降低相关失效根本原因、耦合因子失效率提供了方法与途径，确保大型复杂系统处于安全稳定的运行环境之中。

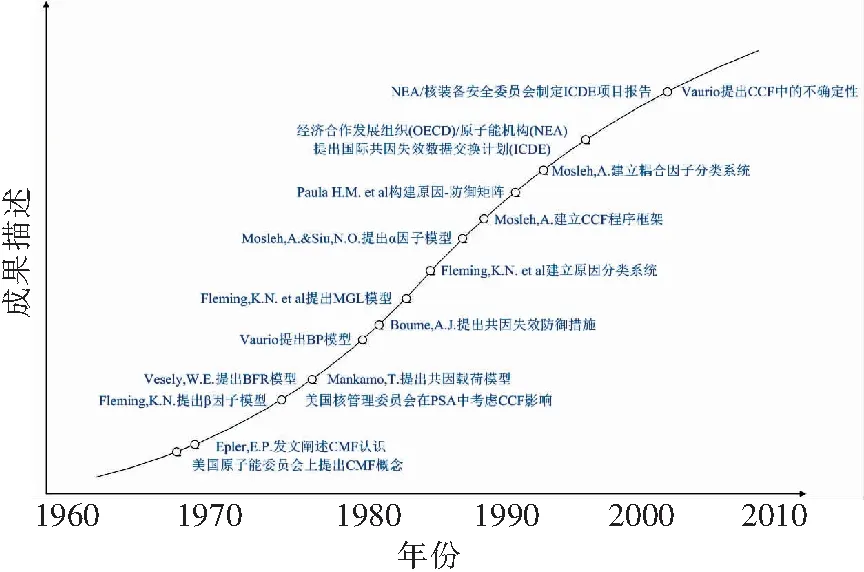
图2 相关失效发展历程Fig.2 Development history of dependent failure research

3 相关失效分析的常用方法

在缺乏相关数据信息的情况下，为提高复杂系统的可靠度，在进行相关失效分析时，详细、全面的定性分析能够有效地减少相关失效事件的发生概率。在复杂系统中，相关失效定性分析包括相关失效机理分析和相应的防御措施。相关失效机理分析包括[9]：1)确定元件失效的根本原因，涉及装备制造、旋工、安装、调试等多个环节；2)确定对同一失效事件具有敏感性的一组元件的耦合因子，如同样的结构设计、制造工艺、功能设定、安装位置、环境条件、维护规程、操作方法等。防御措施包括根本原因的防御和耦合因子的防御：1)可以减小系统中单一元件的失效概率以降低多重失效事件的故障率，从而防止元件相关失效事件的发生，如在设计、制造、安装等环节加强质量管控、设置屏障防止外部事件引起设备失效等；2)由于防御根本原因无法从根本上防止相关失效事件的发生，从防御的角度来看，更多的是防御耦合因子，包括功能、设备和人员的多样化、设置空间隔离、物理防护等屏障、进行阶段性测试与维护。随着测试技术、监测手段、无伤检测等技术的发展与广泛应用，在复杂系统相关失效分析中可以获取越来越多的数据信息，实现以定量计算为主、定性分析为辅的转变。

由于共因失效在相关失效中约占80%的比重，因此，主要针对共因失效的建模方法进行分析。共因失效定量计算的模型与方法一般基于Poisson模型。以由个元件组成的共因元件组为例，一般作出如下假设：

1)系统元件在无共因事件发生时，寿命独立同分布，服从指数分布；

2)系统受到共因失效冲击造成k个元件失效的事件记为Ek，Ek发生的时间间隔独立同分布，服从指数分布(1≤k≤m)；

3)导致事件E1，E2，…，Em发生的共因失效冲击之间彼此独立，与各基本事件的失效相独立；

4)k个元件同时失效的失效率λk与失效元件个数有关，与具体元件无关；

5)对于系统中的各种失效事件能被发现，并立即采取维修手段且维修时间不计。

因此，模型中的可靠性参数可以表示为

(12)

当λk≪0时，Qk≈λkt。

3.1β因子模型

Fleming在1975年提出β因子模型，并将β定义为元件共因失效率与总体失效率的比值[10-11]，表示为

(13)

式中：λc为共因失效率；λt为元件总失效率；λI为独立失效率。

β因子模型作出了一个重要假设：当有共因事件发生时，系统中的全部元件失效，则m阶系统基本事件的故障发生率为：

(14)

从式(14)中可知，当系统的元件数量大于2时，中间数量的元件失效率将为0，即Q2=Q3=…=Qm-1=0。而在工程实践中，当共因失效发生时，系统中任意数量的元件同时失效，而不一定只有2个。因此，该模型适用于二阶冗余系统而不适用于多阶冗余系统。β因子模型简单，曾经被广泛应用于概率风险分析和可靠性分析中。

3.2 基本参数模型

基本参数模型(Basic Parameter Model, BPM)[12-13]是Fleming等在式(11)的基础上提出的参数模型，即直接从系统元件的失效数据中确定基本事件失效率Qk，其估计值为

(15)

式中：nk为m阶系统中任意k个元件失效次数；ND为系统需求次数，若为时间型失效，则由系统运行时间T代替ND。

从式(15)可知，当nk=0时，Qk=0，表示当观察失效次数为0时，所得到的事件失效率为0，即基本参数模型存在无法确定未观察到的失效阶数的失效率。然而，相关失效事件是小概率事件，尤其是对于高冗余复杂系统，高阶失效数据更加难以观察和获取，这就限制了BPM的推广应用。

3.3 多希腊字母模型

针对β因子模型存在的问题，Fleming等在β因子模型的基础上于1986年提出了多希腊字母模型(Multiple Greek Letter, MGL)[14]。为了表达在高阶冗余系统中共因失效事件引起不同数量元件的失效，引入了β、γ、δ等多个参数。对于由m个元件组成的共因元件组需要(m-1)个不同参数，模型参数的一般表达式为

(16)

(17)

(18)

(19)

式中：β为当某一指定元件失效时，系统中2个或2个以上元件失效的概率；γ为当某一指定元件失效时，在2个或2个以上元件失效的条件下，系统中,3个或3个以上元件失效的概率；δ为当某一指定元件失效时，在3个或3个以上元件失效的条件下，系统中4个或4个以上元件失效的概率。

方便起见，MGL中的参数用ρi表示，则有ρ1=α，ρ2=β，ρ3=γ，ρ4=δ，…，ρm+1=0。在MGL模型中的基本事件概率可以表示为

(20)

参数的最大似然估计为

(21)

式中：nk为系统中k个元件同时失效的次数；knk为系统中k个元件同时失效的总元件数。

显然，MGL模型是β因子模型的扩展与推广，由于考虑了多重失效等因素，性能远远优于β因子模型。模型参数的数量与共因元件组元件数量的多少m相关，m越多参数越多，并且不同数量的共因元件组的参数不相同，无法统一使用，因此，MGL模型增加了多元件系统进行参数估计的复杂性。相比于BP模型，MGL模型参数也是以失效元件数量进行定义，但是由于引入了间接参数ρi，在缺乏多重失效数据的情况下，可以依靠专家经验和各元件的相关性对参数ρi进行直接赋值，从而避免了无多重失效数据时模型不可应用的问题。但是，专家经验的引入带来了一个新的问题，即认知不确定性，这也限制了MGL模型在高阶冗余系统中的应用。

3.4 α因子模型

A.Moslen和N.O.Siu在1987年提出α因子模型，把模型参数定义为[15-16]：ak表示由于共因失效造成k个元件同时失效的概率与系统总失效率的比值。以一个由m个元件组成的共因元件组为例，有

(22)

QS表示系统的总失效率，即

(23)

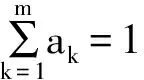
虽然系统的总失效率QS难以确定，但是可以确定元件的总失效率Qt，有

(24)

Qk由ak和Qt表示为

(25)

ak的极大似然估计为

(26)

从式(25)可知，相比于MGL模型，α因子模型也考虑了多重失效的特点，参数的数量随着系统元件的增加而增加。从式(26)可知，α因子模型也存在零失效数据导致零失效率的问题，虽然可以采用专家意见进行解决，但同样带来了认知不确定性问题。

3.5 二项失效率模型

二项失效率模型(Binomial Failure Rate, BFR)[17-18]由Vesely在1977年提出，当时考虑了正常环境载荷下元件独立失效和由冲击引起的失效两种类型的失效。Atwood于1983年将冲击失效分为致命冲击和非致命冲击两种类型。相比于前4种模型，BFR属于冲击模型，用失效率描述基本事件的发生概率。

在BFR模型中作出如下假设：当致命冲击发生时，所有元件以1的概率失效；当非致命概率发生时，共因元件组的各个元件以概率p独立失效，失效的元件数量服从二项分布B(m,p)。由m个相同元件组成的共因元件组中各基本事件的发生率表示为

(27)

式中：λI为单个元件独立失效概率；v为非致命冲击发生概率；p为非致命冲击条件下元件的条件失效率；w为致命冲击发生率。

BFR模型具有4个参数，且不会受到系统元件数量多少的影响，根据失效数据估计出的参数值就可以预测任意重事件的失效率，从而避免了类似于MGL模型和α因子模型中出现的零失效数据问题。然而，BFR模型作出的非致命条件下的元件失效独立性假设忽略了不同的根本原因将导致不同的共因失效的这一问题。在工程实践中，环境改变、错误维修、错误使用等造成的冲击具有随机性，而在非致命条件下，元件的失效率具有随机性，元件之间又具有相关性。BFR模型的假设导致了其应用结果存在较大的偏差，因此限制了其在概率风险评估中的应用。

4 相关失效分析未来的研究方向

4.1 不确定条件下的相关失效分析

复杂系统相关失效分析的定量计算基于对已经发生的相关失效事件的描述，而在对相关失效事件进行描述时引入了诸多不确定性因素，包括数据不确定性、模型不确定性、统计不确定性。通过模型改进与细致分析可以减小或消除模型不确定性，而统计不确定性源于数据不确定性，即对相关失效事件描述不够全面和特定相关失效事件数据缺乏。针对数据缺乏的情况，必须借助已经发生相关失效事件的其它复杂系统的统计数据，并将这些已知相关失效事件转换到待分析的复杂系统中。Jussi K. Vaurio[16]提出了基于相关映射的影响向量法，将不同数量相似元件的相关失效数据转换到待研究的复杂系统中解决数据缺乏问题，包括向上映射和向下映射。但是，由于不同的复杂系统在运行条件、环境、特性等方面存在着差别，因此需要对影响向量法进行修正以将这种差别缩小到最小。

4.2 多状态条件下的相关失效分析

关于复杂系统失效与退化的共因失效分析研究大都基于二元状态假设，即从故障树分析、事件树分析的角度出发的正常与故障分析，忽略了元件与系统介于正常与故障之间的中间状态。随着退化理论、多状态理论等研究的深入，需要在分析CCF发生机理的基础上，对二元状态CCF分析向多状态分析拓展。李春洋等[19]针对传统二元状态与相对独立假设存在过于简单化，不能反映系统的真实情况的问题，研究了共因失效分析条件下多状态复杂系统的冗余组件优化配置问题。但是，由于研究偏向于可靠度与费用约束条件下的配置优化，所建立的模型相对简单。相对于竞争失效分析，相关失效分析具有一定的复杂性，并且实验数据获取方面存在一定难度，因此，当前的理论研究还不够深入，主要局限于二元状态系统与简单的多状态系统。借助贝叶斯网络、D-S证据理论等理论在因果推理、数据融合方面的优势，借鉴类似复杂系统的实验数据可以建立相应的多状态相关失效情况下的分析模型，并可以实现不确定性条件下的正向与反向推理。

5 结束语

建立在相对独立的二元状态基础上的可靠性模型偏于保守，往往获得较为乐观的评估结果，出于系统结构、环境因素、人为因素等原因，越来越复杂的大型系统元件之间、子系统之间的相互关系使得失效事件之间不再是相对独立的，而是相关的。借助现有的相关失效分析模型及其改进模型、概率理论、Monte Carlo仿真、神经网络等方法可以对相关失效事件进行可靠性分析。随着多状态系统的发展完善，在传统二元状态的基础上逐渐建立多状态的相关失效分析模型，以解决“正常”到“故障”之间的“渐变”问题。在进行多状态相关失效分析的同时，可以进行剩余寿命预测、故障预测等相关分析，为维修保障决策的制定提供理论与技术支持。将认知不确定性引入复杂系统的相关失效分析中，可以有效解决多希腊字母模型、α因子模型等模型中专家信息引入带来的不确定问题，进而提高评估结果的精确性与可信度。

[1] 张振友,郭强,黄立坡,等. 基于马尔可夫过程的武器系统相关失效分析[J]. 火力与指挥控制,2012,37(7):117-119.

[2] 王学敏,谢里阳,周金宇. 考虑共因失效的系统可靠性模型[J]. 机械工程学报,2005,41(1):24-28.

[3] Ram M, Singh S B. Analysis of a complex system with common cause failure and two types of repair facilities with different distributions in failure[J]. International Journal of Reliability and Safety,2010,4(4):381-392.

[4] 闫明,张义民,李鹤,等. 机械零件相关失效可靠度计算的二重积分模型[J]. 东北大学学报:自然科学版,2011,32(10):1460-1463.

[5] 李翠玲. 系统相关失效概率模型及其不确定性分析[D].沈阳:东北大学,2005:21-38.

[6] Ramirez-Marqueza J E, Coit D W. Optimization of system reliability in the presence of common cause failures[J]. Reliability Engineering and System Safety,2007,92(10):1421-1434.

[7] Vaurio J K. Extensions of the uncertainty quantification of common cause ailure rates[J]. Reliability Engineering and System Safety,2002,78(1):63-69.

[8] Muhammad H, Hidekazu Y, Takeshi M, et al. Common cause failure analysis of PWR containment spray system by GO-FLOW methodology[J]. Nuclear Engineering and Design,2013,262:350-357.

[9] 方云根,曾小清,王刚. 轨道交通列控系统共因失效分析[J]. 上海交通大学学报,2015,49(7):1052-1057.

[10] Jin H, Rausand M. Reliability of safety-instrumented systems subject to partial testing and common-cause failures[J]. Reliability Engineering and System Safety,2014,121(1):146-151.

[12] Pan Z J, Nonaka Y. Importance analysis for the systems with common cause failures[J]. Reliability Engineering and System Safety,1995,50(3):297-300.

[13] Kang D I, Hwang M J , Han S H, et al. Approximate formulas for treating asymmetrical common cause failure events[J]. Nuclear Engineering and Design, 2009,239(2):346-352.

[15] Zheng X Y, Yamaguchi A, Takata T. α-Decomposition for estimating parameters in common cause failure modeling based on causal inference[J]. Reliability Engineering and System Safety,2013,116(1):20-27.

[16] Vaurio J K. Consistent mapping of common cause failure rates and alpha factors[J]. Reliability Engineering and System Safety,2007,92(5):628-645.

[17] Atwood C L, Kelly D L. The binomial failure rate common-cause model with WinBUGS[J]. Reliability Engineering and System Safety,2009,94(5):990-999.

[18] 谢里阳,李翠玲,李剑锋. 冗余系统共因失效概率预测模型[J]. 东北大学学报:自然科学版,2006,27(2):213-216.

[19] 李春洋,陈循,易晓山. 考虑共因失效的多态系统可靠性优化[J]. 中国机械工程,2010,21(2):155-159.

Review on Research on Dependent Failure Analysis of Complex Systems

LI Zhi-qiang1，XU Ting-xue1，GU Jun-yuan1，LIU Yu-dong2

(1.DepartmentofOrdnanceScienceandTechnology,NavalAeronautical&AstronauticalUniversity,ShandongYantai264001,China;2.Unit95080ofPLA,GuangdongShantou515000,China)

With systems developing towards complication, structuration and hierarchicalization, the deficiencies of traditional reliability assessment and analysis on the basis of independence and binary states become serious gradually. The status and impact of dependent failure analysis become more significant in reliability assessment and analysis of complex systems with redundant components. On the basis of introducing dependent failure, common cause failure is defined and applied to expand traditional fault tree. Throughout the development of dependent failure analysis, the advantages and disadvantages of five common methods concerned are summarized, including beta factor model, basic parameter model, multiple Greek letter, alpha factor model and binomial failure rate model. And the research directions of dependent failure analysis of complex systems in the future are predicted, i.e., dependent failure analysis under uncertain conditions and dependent failure analysis for multi-states systems.

reliability assessment; dependent failure; common-cause failure; uncertain condition

2017年1月20日

2017年3月15日

李志强(1988年-)，男，博士研究生，主要从事复杂系统可靠性建模与分析等方面的研究。

TB114.3

A

10.3969/j.issn.1673-6214.2017.02.012

1673-6214(2017)02-0130-07