基于Manhattan距离的汽车总装车间带时间窗多AGV小车调度优化
2017-09-11常建娥莫易敏李佛胜
常建娥 王 璐 莫易敏 张 峰 李佛胜
(武汉理工大学机电工程学院1) 武汉 430070) (上汽通用五菱汽车股份有限公司2) 柳州 545000)
基于Manhattan距离的汽车总装车间带时间窗多AGV小车调度优化
常建娥1)王 璐1)莫易敏1)张 峰1)李佛胜2)
(武汉理工大学机电工程学院1)武汉 430070) (上汽通用五菱汽车股份有限公司2)柳州 545000)
为解决汽车总装车间物料配送AGV的调度问题,针对汽车流水线的布局特征,以AGV小车利用效率最高、数量配置最少为目标建立数学模型,提出了一种改进的两阶段启发式算法.通过基于Manhattan距离、时间聚集度的启发式分类算法将物料配送点进行聚类;按照聚类的结果,以及物料配送点的优先级,得到优化后AGV的行驶路径.最后通过某汽车企业总装车间多AGV调度优化的实例,与原先的调度方案进行结果对比,验证了该方法的有效性和可行性.
汽车总装车间流水线布局;Manhattan距离;时空聚集度;AGV调度优化
0 引 言
多车型混流生产模式下,零部件种类、数量增多,给总装物流带来一系列的挑战,例如,线旁物料存储面积不够,物料配送频次增多,物料配送不及时导致的停线次数增多等.面对这些挑战,各主机厂纷纷采取自动导航小车(automated guided vehicle,AGV)拉动单台份物料的SPS(set parts supply)配送模式,来满足混流生产物流需求.
在SPS物料配送模式中,最重要的是确定AGV的行驶路线,即AGV的路径规划问题,其本质上是VRP(vehicle routing problem)问题.国内外对AGV的调度研究主要集中在AGV的路径规划、AGV的数量配置以及AGV的任务分配三个方面.同时也分为单AGV和多AGV系统的调度问题.Wassan[1]提出一种基于变邻域搜索方法来求解MT-VRPB;Abel等[2]针对多目标的VRPB问题提出了一种基于相似性选择的进化算法;于滨等[3]提出一个两阶段的启发式算法研究带时间窗的多中心车辆路径优化问题(MDVRPTW);黄一钧等[4]借助排队论模型,以最小总成本为目标建立了AGV小车数量配置计算模型;刘健等[5]基于Plant Simulation建立了某电表自动化检测线中的AGVS模型,通过分析其仿真运行状况确定系统所需AGV的最佳数量;朱琳等[6]提出一种改进的遗传算法对配料区AGV小车进行了任务分配的优化并通过仿真的手段对配料区的物料储存布局进行了优化改进;边培莹等[7]以提高生产效率为目标,提出了一种基于粒子群算法的AGV动态调度策略,均衡多个AGV的任务量,并使得AGV数量总体最优;Qi等[9]综合考虑空间距离和时间要求,对需求点进行划分,提出了一种基于时空距离的聚类思想,用于多任务的调度.
以上研究多集中在单AGV的路径优化、多AGV运输总距离最小以及物料配送系统中AGV数量配置最少的规划问题.而汽车总装车间布局模式以及精益生产要求物料及时配送,对AGV路径规划问题提出新的挑战.本文对SPS物料配送系统中的多AGV多个任务请求的调度优化进行研究,针对汽车总装流水线布局特征,采用基于Manhattan距离、时间聚集度的两阶段启发式算法,得到多个AGV任务分配的优化结果和单个AGV的优化路径.
1 汽车总装生产特征分析
在汽车总装车间,根据装配顺序与工艺,分为内饰、底盘与终线三部分,而这些工段通常是平行布置的.为了提高装配效率,一般对大件总成物料采取模块化供货,即在内饰、底盘、终线工段旁建立平行于工段的车门、仪表盘、发动机分装线,以及座椅、轮胎的输送链运送物料到线旁.因此形成了间隔式Bay Layout布局[10].
此外,随着汽车制造技术的发展,总装车间生产节拍普遍达到了40JPH(job per hour),有些甚至达到了60JPH,即在1 min之内装配完一辆车.在混流生产模式下,装配流水线上每个工位每种车型所需物料也都不一样,要满足高节拍生产装配,需要保障物料配送的及时性,即AGV的配送有时间窗要求.
为了满足多品种、中小批量、高节拍的混流生产模式的物料供应,大部分主机厂都采用SPS物料拉动模式.其运作模式大致如下:在配载区将单台份物料装载到SPS料车上,由AGV将其配送到指定上线点;随即AGV行驶至SPS空料车下线点,回收SPS空料车送到配载区;AGV回到充电点进行周期性充电,接着开始下一周期的配送任务.即AGV需要在指定的时间点到达指定的途经点,形成一个回路.
综上所述,汽车总装车间多AGV的任务调度问题是一个基于汽车总装车间Bay Layout布局的带时间窗的路径规划问题VRPTW(vehicle routing problem with time window),其最终目标是提高送料AGV的利用率,减少AGV的配置数量,从而降低物流设备的投入成本、降低物流费用.
2 基于Manhattan距离与时空距离的路径规划问题
2.1 汽车总装车间AGV途经点Manhattan空间距离
汽车总装车间工段之间大多是间隔式布局.而在Bay Layout布局下,AGV途经点之间的距离是不能用两点之间的直线段即常用的欧式距离来计算的.图1为汽车总装车间两个工段布局的简化图,由于AGV的磁带轨道是平行于工段进行铺设的,且不能直接越过工段,因此只能按照上述箭头所指的“正交路线”运动.鉴于汽车总装车间流水线Bay Layout布局对AGV运动路径的限制,本文基于Manhattan距离,计算并修正AGV途经点之间的距离,得到最接近现实的途经点距离.

注:A,B,C,D,E为装配工位;M,N为内饰一、内饰二工段的定点位置坐标.图1 汽车总装车间工位Manhattan距离示意图
在计算工位之间距离时,可以分为流水线两工段之间工位(inter-bay)与流水线工段内工位(intra-bay),计算公式为
A.B距离=Manhattan距离=
(1)
(2)
应用修正后的Manhattan距离可以较为精确的计算AGV途经点之间的距离,从而能得到更合理的途经点聚类结果.
2.2 汽车总装车间AGV途经点时间距离
汽车总装车间高节拍下的装配生产需要稳定、准时的物料配送做保障,配送AGV要在途经点所限定的时间窗内到达.因此,在对AGV进行任务分配时,不仅要考虑途经点间的空间距离,还要考虑其时间窗的关系.如果两个途经点的空间距离很近,但时间窗上相隔较久,则AGV在到达下一个制定位置之后还需要等待一段时间才能够进行作业,会产生浪费;反之亦然.用时间距离DijT来度量两个途经点被相继被同一辆AGV服务的便利程度,时间距离越小,则两个途经点越容易被同一辆AGV服务;时间距离越大,则两个途经点就越不容易被同一辆AGV服务.
假设一辆AGV依次经过点i和点j,其时间窗分别是Ti=[a,b]和Tj=[c,d],设a≤c,从点i到点j需要花费的时间为tij,假设在每个途经点不作停留.
1) 若tij>d-a,即AGV从点i到达点j所需要的时间大于途经点之间的最长时间间隔,AGV无法在同一任务中同时经过点i和点j,因此,将途经点i和j的时间距离设为无穷大.
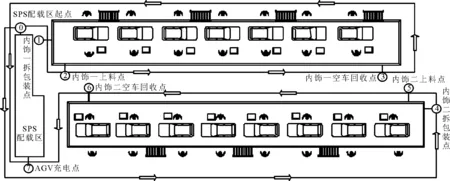
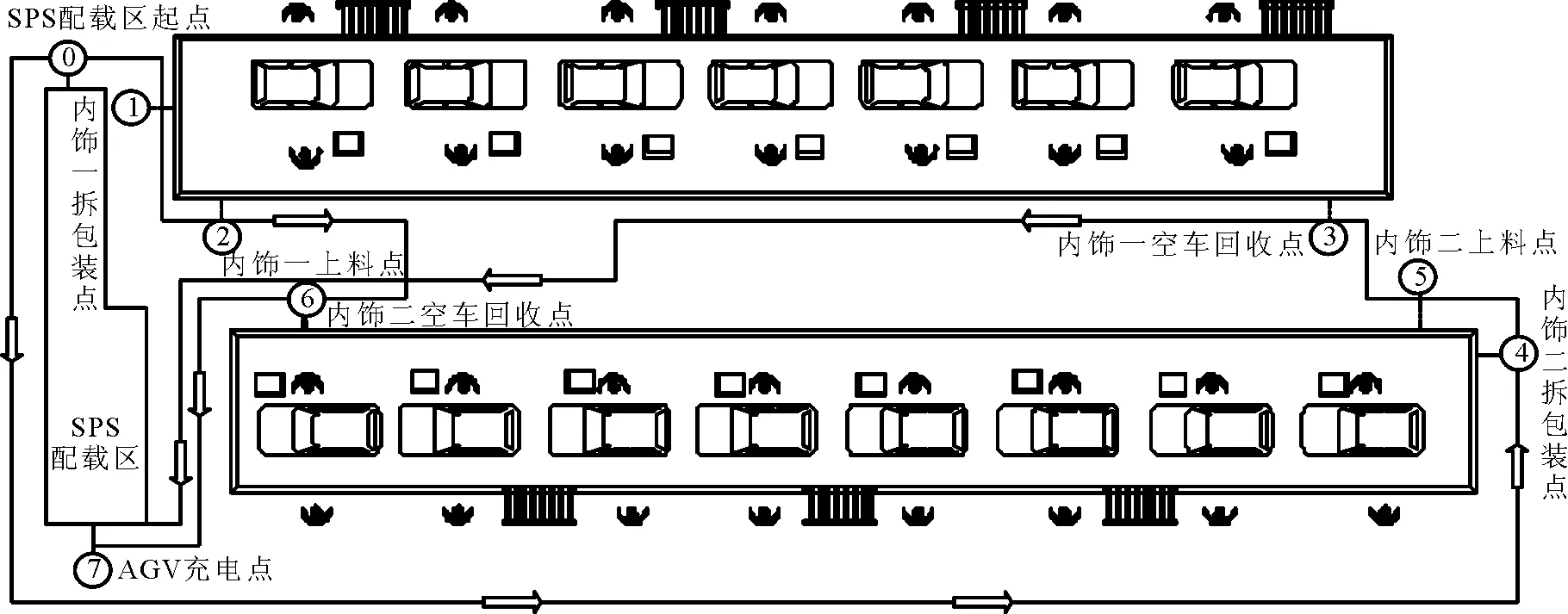
2) 若c-b 3) 若tij 综上所述,时间距离的计算公式为 (3) 2.3 汽车总装车间AGV途经点时空距离归一化 汽车总装车间送料AGV的任务是在规定的时间内将规定的物料零部件配送到指定工位,既有空间距离上的要求,又有时间限制.一般的聚类方法都只以空间距离为分类依据,鲜少同时考虑到空间距离与时间窗要求. 文献[9]借用时间地理学中的时空路径概念来表达车辆的路径,其中二维坐标平面表示空间位置,垂直坐标表示时间窗.根据这一原理,汽车总装车间VRPTW问题的解也可以表示为AGV的时空路径.图2为汽车总装车间AGV时空路径示意图. 图2 汽车总装AGV车间时空路径示意图 由图2可知,AGV小车从O点出发,必须在时间窗要求内依次达到各个途经点配送物料、回收空车、进行周期性充电等,且AGV的运动路径受限于总装车间工段及分装线的布局,只能按照图中的“正交”路径行驶. Ds′ij=DTij×v (4) (5) 3.1 汽车总装车间AGV调度优化模型 如果对AGV任务分配得不合理,就会导致有些AGV的配送任务过多、配送路径过长,使得有些区域的物料配送不及时,很容易影响生产节拍甚至造成停线.为了保障混流生产,需要合理正确地将任务分配给多个AGV,并规划出其行驶路径,使得AGV的利用率最高. 汽车总装车间多AGV的任务调度优化问题存在以下假设和约束: 1) 汽车总装车间各工段各工位布局及AGV可行走的路径通道已经确定,即途经点的空间坐标、时间窗要求以及任务优先级已知. 2) 每辆AGV初始位置在集配区的充电桩处,当AGV完成上料工位物料配送以及空车回收任务之后回到初始位置进行充电. 3) 任何任务都可以分配给其中一辆AGV,且每辆AGV都相同. 4) AGV能够满足SPS料车上线任务和SPS空车下线任务的载重. 5) 每个指定的途经点都要被经过,且每个途经点只能由一辆AGV经过一次. 6) 满足每个途经点的时间窗要求,否则不可行. 在汽车总装车间内有一个SPS集配区,多辆配料AGV可供调度.整个汽车总装车间有多个途经点,可分为SPS料车上线点、SPS空车下线点、配载区AGV装载点以及配载区AGV充电点四类,不妨设途经点的编号为i∈{1,2,…,M},其中每个途经点表示为Ci(xi,yi,ti),xi为途经点的横坐标;yi为途经点的纵坐标;ti=[tis,tie]为途经点的时间窗要求;AGV的编号为k∈{1,2,…,N};每辆AGV可经过多个途径点,AGV的途经点编号为s∈{1,2,…,P},设SPS物料集配区编号为0.在上述假设和约束的前提下,使得汽车总装车间AGV利用率最高,AGV总数最小,每辆AGV分配到的任务的时空距离最小,建立数学模型为 (6) mink (7) λik0=0,∀i,k (8) λik1≥λik2≥…≥λikp,∀i,k (9) (10) 式(6)为每辆AGV所分配到的途经点的时空距离之和最小;式(7)为AGV数量最少;式(8)为每个途经点只由一辆AGV经过;式(9)为每辆AGV的初始位置在SPS物料配载区;式(10)为每个途经点从每辆AGV的第一个途经点开始依次排列,保证每辆AGV的多个途经点是连续排列的. 3.2 基于K-means算法的汽车总装车间AGV调度模型求解 聚类是根据途经点两两之间的时空距离来对其进行分组,使得组内途经点之间的时空距离较小,而组间较大.划分聚类问题是NP-完全问题.而对于汽车总装车间装配流水线来说,上料工位个数有限,而K-means算法在小范围空间聚类被证明是稳健的,因此采用K-means算法基于时空距离对AGV途经点进行聚类. 传统的K-means算法的基本思想是:随机或人为给定初始聚类中心点,按照最邻近原则,将剩下的点根据距离被分配到距其最近的中心点.然后在不断迭代的过程中,中心点不断改变,以便聚类的族群更密集地分布.文中采用修正后的Manhattan距离结合时空距离,设计了基于时空距离的K-means聚类的解决方法.具体计算过程为: 步骤1 确定聚类的数目 根据实际生产经验,k(即AGV的配置数量)一般不会设置很大,可以通过枚举,令k从2到一个固定值如10,在每个k值上重复运行数次K-means,并计算当前k的平均轮廓系数,最后选取轮廓系数最大的值对应的k作为最终的集群数目. 步骤2 随机选取k个初始中心点,依据Manhattan时空距离计算公式,计算其余点和初始中心点的空间距离和时间窗距离,选取ω1=0.5,ω2=0.5,将时空距离进行归一化处理,按照最邻近原则,划分到相应的类别. 步骤3 在初始分类的结果上按平均值的方法重新计算聚类中心点,再重复步骤2,进行迭代. 步骤4 直到最后每个类组内时空距离之和最小,算法收敛,聚类数目最小且不再变动,则结束. 4.1 汽车总装车间平面布局及相关数据 以某汽车企业总装车间内饰工段为例,利用基于时空距离的K-means聚类算法对其总装车间内饰工段的送料AGV任务分配和排序进行优化.该汽车总装车间采用SPS物料拉动模式,设有一个SPS物料配载区,放置内饰一和内饰二工段的SPS物料.当装配流水线上缺少物料时,AGV拉着满载的SPS料车从配载区出发,将SPS料车送至相应工段的上料点,然后空车下线点回收SPS空车,回到配载区卸下空车并进行周期性充电.每个工段有一个上线点,一个下线点,一个拆包装点,图3为汽车总装车间内饰工段现行AGV行驶路径示意图. 图3 汽车总装车间内饰工段现行AGV路径示意图 由图3可知,一组AGV负责内饰一工段,其行驶路径如红线所示;另外一组AGV负责内饰二工段,其行驶路径如绿线所示.两组AGV均随行于SPS料车,在SPS料车上线之后到下线之前AGV均处于空载等待状态,导致AGV单次运行周期过长,需要配置较多的AGV来满足物料的实时配送.内饰工段途经点的坐标以及时间窗要求见表1. 4.2 优化结果及分析 为最大限度提高AGV的利用率,减少AGV的数量配置.下面依照上述基于Manhattan距离的时空聚类方法对AGV的任务分配进行优化. 对两两途经点之间的Manhattan空间距离以及时间窗距离进行计算,并最终进行归一化处理得到时空距离,并依据时空距离对其进行聚类,聚类结果为 表1 各途经点的空间坐标及时间窗要求 AGV1:0-1-2-6-7 AGV2:0-4-5-3-7 内饰一 AGV由SPS配载区起点出发,经过内饰一物料拆包装点,到达内饰一SPS料车上线点,后穿过内饰一和内饰二过道,到达内饰二SPS料车下线点,拉回内饰二空料车回到SPS配载区充点电进行周期性充电. 内饰二 AGV由SPS配载区起点出发,穿过内饰一和内饰二过道到达内饰二物料拆卸点,然后达到内饰二SPS料车上线点,再穿过过道去内饰一SPS料车下线点拉回内饰一空料车回到SPS配载区充电点进行周期性充电. 优化后的两组AGV的行驶路径示意图见图4. 图4 优化后内饰工段AGV行驶路径示意图 由图4可知,配料AGV的任务分配不再只是按照工段,二是依据时空距离就近进行分配.很明显,配送内饰一SPS料车以及回收内饰二SPS料车的一组AGV的单次配送时间缩短,由原来的1 252 s缩短到610 s;配送内饰二SPS料车以及回收内饰一SPS料车的一组AGV单次配送时间也有小幅降低,由原来的2 008 s缩短到1 736 s. 按照60JPH,一辆AGV单次周期配送三辆SPS料车进行计算,任务分配优化后,汽车总装车间内饰工段配料AGV的数量缩减为 内饰一工段:(1252-610)/(3×60)=3.57≈3 内饰二工段:(2008-1736)/(3×60)=1.51≈1 即通过基于Manhattan距离结合时间窗距离的时空聚类方法来分配AGV的任务点,能够在一定程度上减少AGV的空载等待以及AGV的空载行驶距离,提高AGV的利用率,从而缩短AGV的单次配送周期,最终减少AGV的配置数量,降低物流配送成本. 针对多途径点带时间窗的多AGV任务分配问题,根据汽车总装车间的Bay Layout布局,对途经点之间的Manhattan距离进行了修正,提出了改进的基于时空距离的K-means算法,将优化方法运用到某汽车企业总装车间内饰工段配料AGV的调度上,改进后的方案使得AGV的单次配送周期缩短、AGV的利用率提高、总的AGV配置数量减少,证明了该优化方法的有效性.本文对实际的多AGV任务分配问题进行了一定程度的简化,忽略了物料的装卸时间和可能出现的AGV碰撞问题.在今后进一步的研究中,可以考虑存在碰撞情况下AGV路径的规划问题. [1]WASSAN N. The multiple trip vehicle routing problem with backhauls: formulation and a two-level variable neighbourhood search[J]. Computers and Operations Research, 2016(1):55-58. [2]ABEL G N, JOHN A, MIGUEL A,et al. An evolutionary approach for multi-objective vehicle routing problems with backhauls [J].Computers & Industrial Engineering,2015,81:90-108. [3]于滨,靳鹏欢,杨忠振.两阶段启发式算法求解带时间窗的多中心车辆路径问题[J].系统工程理论与实践,2012,32(8):1793-1800. [4]黄一钧.车身车间AGV物料搬运系统小车数量配置规划[J].工业工程与管理,2016(4):156-162. [5]刘健,黄奇峰,王忠东,等.基于Plant Simulation 的AGV输送系统仿真分析及其应用[J].现代制造工程,2013(11):13-19. [6]朱琳,范秀敏,何其昌.柔性生产系统配料区多自动导航小车调度优化[J].计算机集成制造系统,2012(6):1168-1175. [7]边培莹,李德信,包宝军,等.粒子群算法在生产物流调度中的应用研究[J].计算机工程与应用,2010,46(17):220-223. [8]戚铭尧,张金金,任丽.基于时空聚类的带时间窗车辆路径规划算法[J].计算机科学,2014,41(3):218-222. [9]QI M Y, LIN W H, LI N,et al. A spatiotemporal partitioning approach for large-scale vehicle routing problem with time windows[J].Transportation Research Part E, 2012,48:248-257. [10]WANG H F, CHANG C M. Facility layout for an automated guided vehicle system[J]. Procedia Computer Science, 2015,55:52-61. Multiple AGVs Scheduling with Time Windows in the Automotive General Assembly Shop Based on the Manhattan Distance CHANG Jian’e1)WANG Lu1)MO Yimin1)ZHANG Feng1)LI Fosheng2) (SchoolofMechanicalandElectronicEngineering,WuhanUniversityofTechnology,Wuhan430070,China)1)(SAIC-GM-WULINGAutomobileCo.Ltd.,Liuzhou54500,China)2) To solve the scheduling problem of material distribution AGVs in the General Assembly shop, the paper proposes an improved two-phase heuristic algorithm based on the layout of the automotive assembly line and develops a mathematical model which aims at the highest utilization and the minimum quantity of the AGVs. Firstly, the material demanding stations with the heuristic sorting algorithm are clustered based on both the Manhattan distance and the time requirements. Besides, according to the results of clustering and the priority of material demanding stations, the optimal paths of AGVs are scheduled. At last, through AGVs scheduling examples in the automotive GA shop, the feasibility and the validity of this method are verified based on the comparison with its former AGVs scheduling scheme. the layout of the automotive assembly line in the GA shop; the Manhattan distance; concentration of time and space; AGV scheduling optimization 2017-05-26 TP391 10.3963/j.issn.2095-3844.2017.04.011 常建娥(1962—):女,硕士,教授,主要研究领域为机械设计与理论、物流工程

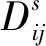
3 模型的建立与求解
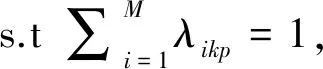
4 案例分析

5 结 束 语
