基于遗传算法的油田群水域航路规划模型研究*

马全党 彭宇飞 何 颖 江福才

(武汉理工大学航运学院1) 武汉 430063) (内河航运技术湖北省重点实验室2) 武汉 430063) (深圳招商蛇口国际邮轮母港有限公司3) 深圳 518000)

基于遗传算法的油田群水域航路规划模型研究*

马全党1,2)彭宇飞1,2)何 颖3)江福才1,2)

(武汉理工大学航运学院1)武汉 430063) (内河航运技术湖北省重点实验室2)武汉 430063) (深圳招商蛇口国际邮轮母港有限公司3)深圳 518000)

为了保障油田群水域船舶通航安全，选择油田群水域船舶航路规划模型作为研究对象，立足于将现有最优化理论有效的应用于油田群水域航路规划问题中，旨在对油田群水域内的通航船舶做系统的航路规划.提出了多目标航路规划模型，并利用遗传算法求解最优路径，为油田群水域的航路规划、安全监管等方面提供理论支撑和技术支持.

油田群水域；遗传算法；转向角；适应度函数；航路规划

0 引 言

海底油气资源蕴藏较丰富的水域群聚性的分布着钻井平台，平台本身的碍航性和服务船舶的频繁活动使得油田群水域的通航环境日益复杂[1].因此，海上钻井平台以及平台服务船舶与过往油田群水域的其他船舶之间的碰撞风险大大增加，该水域的通航安全和防污形势日趋成为当今航海界备受关注的焦点问题.在充分考虑油田群水域复杂通航环境基础上，合理的规划约束过往船舶通航路径即做好航路规划，能减少船舶的碰撞几率，改善和优化该水域的通航环境[2].

郭禹[3]在对典型水域船舶追越问题的探究中提出了能见度不良情况下最小安全追越距离的概念，尤其对分道通航中的追越问题做了详细和深入的研究.提出了标准分隔宽度可以作为计算船舶通航分道尺度的理论依据的说法.刘敬贤等[4]基于渤海湾水域多种通航环境因子量化解析结果，提出了渤海水域的船舶定线制最优比选方案.刘莹[5]提出了一种基于改进蚁群算法的航路规划方法，改进了人工绘制航线费时费力、不准确，以及应用范围狭窄的缺陷.沈崇松[6]在充分考虑渤海海域油田平台碍航性和油田服务船舶操纵性能的基础上对平台安全区范围进行定量研究，为过往船舶和油田服务船舶在油田群水域的避让行动提供了必要的理论支撑.

油田群水域航路规划属于多目标非线性寻优范畴，实现过程较为繁琐和复杂，其核心问题是统筹处理多个优化目标[7-8].航路规划既要考虑通航安全性，又要兼顾经济性，力求航程较短，同时还要考虑船舶操纵性能、操船者的主观意识，以及通航环境因素.遗传算法具有的内在隐蔽性和全局等寻优能力使得其仍是当前处理多目标最优化问题时最佳的工具和方法[9].

1 多目标航路规划目标函数设计

1.1 航路安全

航路安全是指规划的航路能最大限度地保障船舶通航安全，避免与海洋平台发生碰撞等事故，航路安全是航路规划问题中最重要、也是最基本的期望指标之一.本文利用规划航路与海洋平台的距离d作为安全性能的评估依据，这种方法较为简单且易于实现.本文对海洋平台划定了安全领域，所以认为安全领域外的水域均为可航水域，为了保证可航水域无差别性，拟利用航路是否穿越海洋平台安全领域为判断标准.

航路安全性度量标准是海洋平台与航路点距离越大越好，目标函数是求解最小化问题，即

(1)

(2)

式中：dj为海洋平台与航路点之间的距离；Rs为海洋平台与航路点之间的安全距离；ro为惩罚函数，要取得合适，惩罚值过大或过小都可能使收敛得到不合理的解.

1.2 转向角

考虑到船舶操纵性较为特殊，尤其是大型船舶，通常操纵性较差，主要体现在航行过程不能进行大幅度转向操作，所以希望船舶在航行过程中的航路没有大幅度转向，从而保证船舶通航的安全性和稳定性.本文借用航海习惯中船舶转向角越小，船舶越稳越安全的方法，将一次性转向角度限定为不超过30°，且角度越小，航路越优.

根据本文设定，规划航路中存在n个结点时，包含了n-1个航路段，每个航路段间存在着折点，即存在n-2个折点，每个折点即为一个夹角，两个相邻航路的夹角A利用余弦公式求得，见图1.

图1 航路夹角示意图

当角度A越大时，得到的cosA值越小，反之值越大，在航路优化中，考虑到船舶操纵性能有限，船舶转向角不能过大，即期望cosA值越小越好，同时，由于船舶转向角度最好小于30°，设定A≥150°.余弦公式为

(3)

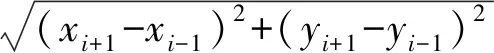
转向角的度量采用夹角余弦来度量，A角度越大，cosA值越小，与最小化求解相匹配的，但是考虑到当A>90°后，cosA为负值，所以本文采用倒数形式设定公式为

(4)

式中：A≥150°

1.3 操船者的主观意识

操船者对于船舶的航线设计一般基于航海习惯，然而计算机自动规划的航路可能不是最符合航海习惯的航路，为了在航路规划中体现航海习惯这一特点，本文将操船者的主观意识作为一个目标指标加入进来.为方便起见，将操船者的主观意识转换为航路引导点来解决这一问题，即在通航环境中设计航路引导点G，G是以(Xg，Yg)为圆心，rG为半径的一个作用圆区域，设定船舶规划的航路必须经过该区域，将航路规划走向引向航海习惯性选择的海域.

设在航路规划中设定航路引导点G，引导点个数有K个，G1，G2，…，GK(K>0)，任一引导点位置Gt=(xt,yt)，半径设定为rG，见图2.

图2 引导点作业区域示意图

设定，任一引导点Gt到航路段pi～pi+1的距离为dti，dt为任一引导点Gt到航路的最短距离.当航路经过该区域时，即视为该航路引导点产生作用，引导点中心到与航路最短距离dt小于引导半径rG，引导作用产生.为了保证作用圆区域内的引导作用一致，此目标的判定也利用圆与线段交点的有无来做标准.

航路引导点与航路距离的计算是与最小化求解相匹配的，鉴于航路只要经过引导点，引导作用就有效这一设定，为了避免引导点认为航路越接近引导点中心的航路越优这一现象.设定当航路与引导点的距离dt≤rG，dt统一取值ro，(ro为罚函数)即设定存在引导点与航路点最短距离小于引导圆半径，航路引导就发挥作用，公式为

(5)

(6)

1.4 航路总航程

航路总航程目标指标是船舶航路规划目标中最基础的问题，对于多目标航路规划问题来说，在其他几个目标指标均满足的情况下，规划的航路航程越短越好.

根据本文设定，航路航程是由各个航段航程累加值，各个航段航程计算公式为

di=d(pi,pi+1)=

(7)

航路总航程的计算也是与最小化求解相匹配的，即求解l的最小值，设定公式为

(8)

2 基于遗传算法的多目标航路规划

2.1 多目标航路规划模型设计

判断矩阵中每一列元素都近似的反映了权值的分配情况，因此采用算术平均法来估计权重值[10]，得

(9)

综合考虑了航路安全性、转向角、操船者的主观意愿和航路长度四项目标，构建了上述目标函数，对目标函数进行量纲一的量化，规范化处理，得

(10)

这些因素的融合构成了新的适应度函数公式为

(11)

(12)

2.2 遗传算法过程

遗传算法需要利用编码设计将表现型转化为基因型，在初始种群产生后，按照达尔文理论适者生存、优胜劣汰的自然进化原理进行进化，通过随机选择算子、交叉算子和变异算子等遗传操作，并对于每一代产生的个体，包括子个体和父个体都要进行适应度的评估，并在其中选择出适应度高的个体，淘汰适应度低的个体，使个体的适应度越来越好，直到抵达最优解[11].

遗传算法的基本步骤如下.

步骤1 编码，参数赋值.

步骤2 产生初始种群p(t).

步骤3 借助适应度函数评估每个体的适应度值.

步骤4 选择算子操作.

p′(t)=Selection[p(t)]

步骤5 重组算子操作.

p″(t)=Rproduction[p′(t)]

步骤6 变异算子操作.

p‴(t)=Mutation[p″(t)]

步骤7 评价群体适应度值.

步骤8 判断是否满足终止进化代数，如满足则输出结果，反之返回步骤4.

3 算法验证

以某油田群水域作为研究背景，该油田群水域以三座中心海洋平台为基础，其余海洋平台发散分布在中心海洋平台周围，大部分海洋平台有海底管线连接，将油气汇集到中心海洋平台后再输送至总部，部分海洋平台由运输船取油运输.图3为具有一般海上石油平台分布特征的典型水域，本文利用此水域对航路规划模型进行验证，该水域海图比例为166∶1，海图信息主要包括港口位置坐标以及海洋平台位置坐标.设定船舶来自天津港方向向港口栈桥码头行驶，即设定起点位置为S1，目地位置为S2，并在通航环境中海洋平台数量较少的水域划定引导点G1.

图3 船舶通航环境处理结果示意图

船舶适应度函数为

(13)

式中：w1=0.34；w2=0.19；w3=0.4；w4=0.07.

图4为目标值变化.由图4可知，目标函数值在0～320迭代次数间呈递减态势，目标函数值锐减，函数值在迭代320次后呈现稳定趋势，整体迭代过程中，函数值下降了8 000，种群收敛效果良好，种群进化时间为10.49 s.

图4 目标值变化

根据遗传算法搜索的航路，来自天津方向的船舶航路规划结果见图5.

图5 船舶航路规划结果

船舶多目标航路规划模型规划的航路总里程为31.6 n mile.航路中存在五个转角，其中最大转角为29.48°，满足大型船舶操纵性能的要求；距离最近的海洋平台为N14，最近距离为2.5 n mile，满足通航安全中与海洋平台最小距离的要求；规划航路与引导圆G1相切而过，引导圆起到了引导作用将规划航路引向海洋平台稀少的海域，规划航路满足多目标航路规划要求.

图6为来自天津方向的BFAL7油船的部分观测航迹图，根据与多目标航路规划模型规划结果(见图5)对比可以看出，多目标航路规划模型规划的航路与实际航线较为契合.因此本文多目标航路规划模型具有科学合理性和工作实用性.

图6 BFAL7油船航迹

4 结 束 语

综合考虑船舶通航安全的多个目标要素，借助遗传算法原理构建多目标函数航路规划模型，并进行模型求解和实例验证，进一步验证了所建模型和计算方法的科学性和可靠性.

本文的研究工作丰富了当前解决油田群水域航路规划问题的理论基础，对保障人民生命财产安全、降低海上油气污染风险、维护航运和石油企业的利益，以及促进油田群腹地经济发展具有十分重要的现实意义.

[1]李豫,钟小侠,曾树兵.浅海边际油田可移动式采油平台综述[C].海洋工程学术会议，厦门:中国造船工程学会近海工程学术委员会,2009.

[2]汤先拓,冯小松,赵望锋.动态规划算法在最优航路规划中的应用[J].广州航海高等专科学校学报,2009,17(2):19-25.

[3]郭禹.航海学[M].大连：大连海事大学出版社,2005.

[4]刘敬贤,韩晓宝,高维杰.渤海海峡海域船舶定线制完善的研究[J].航海技术,2008(5):2-7.

[5]刘莹.改进的动态规划算法在最优航线选择中的应用[J].邵阳学院学报(自然科学版),2007,4(1):14-16.

[6]沈崇松.渤海海域油田平台安全作业区范围研究[J].天津航海,2010(3):28-29.

[7]马全党.典型水域船舶航路动态规划模型及其应用研究[D].武汉:武汉理工大学,2012.

[8]唐坤.车辆路径问题中的遗传算法设计[J].东华大学学报,2002,28(1):66-70.

[9]潘劲松,李腊元.基于GA的动态时延受限多播路由算法[J].武汉理工大学学报(交通科学与工程版),2004,28(1):74-76.

[10]FONSECA C M, FLEMING P J. Genetic algorithms for multi-objective optimization: formulation, discussion and generalization[C]. Proceedings of the 5thInternational Conference on Genetic Algorithms, San Mateo California，1993.

[11]COELLO C A C C, PULIDO G T. A micro-genetic algorithm for multi-objective optimization[C]. First International Conference on Evolutionary Multi-Criterion Optimization，2001(1):126-140.

Shipping Route Planning Model of Oilfield Waters Based on Genetic Algorithm

MA Quandang1,2)PENG Yufei1,2)HE Ying3)JIANG Fucai1,2)

(SchoolofNavigation,WuhanUniversityoftechnology,Wuhan430063,China)1)(HubeiKeyLaboratoryofInlandShippingTechnology,Wuhan430063,China)2)(ShenzhenChinamerchantsShekouinternationalcruisehomeportCo.Ltd.,Shenzhen518000,China)3)

To ensure the navigational safety of oilfield waters, the route planning model in oilfield waters is studied. Applying the optimization theory, the route of ship navigating in oilfield waters is designed systematically. Using genetic algorithm to solve the optimal path, multi-objective route planning model is proposed in this study, which can provide the theoretical foundation and technical support for route planning and safety supervision in oilfield waters.

oilfield waters; genetic algorithm; angle of turn; fitness function; shipping route planning

2017-06-02

*国家级大学生创新创业训练计划项目资助(20161049712002)

U491

10.3963/j.issn.2095-3844.2017.04.021

马全党(1983—)：男，硕士，实验师，主要研究领域为水上交通安全与环境保障