回溯法在物流车动态导航中的应用

王防修,王晓娜,祁华清,赵杰梅

(1.武汉轻工大学 数学与计算机学院,湖北 武汉 430023;2.武汉轻工大学 经济与管理学院,湖北 武汉 430023)

回溯法在物流车动态导航中的应用

王防修1,王晓娜1,祁华清2,赵杰梅1

(1.武汉轻工大学 数学与计算机学院,湖北 武汉 430023;2.武汉轻工大学 经济与管理学院,湖北 武汉 430023)

研究物流车的动态导航问题。由于物流车在配送过程中经常会遇到堵车情况，如果物流车仍按照原最优路径进行配送，则会降低物流车的配送效率。传统的TSP算法只能为物流车规划一个静态最优路径，一旦物流车遇到堵车就无法调整，这样的导航不能提高物流车的配送效率。为了避免上述缺陷，提出了一种用回溯法实现物流车配送的动态优化算法。首先，利用回溯法实现物流车配送的静态优化，将该路径作为物流车的初始路径。如果物流车行驶路径的前方出现堵车，则用回溯法对物流车未配送的客户重新规划一条新的最短路径，通过避开堵车路段来提高物流车的配送效率。如果某个路段的堵车解除而该路段两端的客户还未被配送，则用回溯法对未配送的客户重新规划最短路径来提高配送效率。实验结果表明，利用本文算法进行物流车配送的动态优化算法，能够有效提高物流车的配送效率。

回溯法；动态导航；最优路径；物流车配送；配送效率

1 引言

伴随市场经济的高速发展，物流配送业发展迅猛。合理选择配送路径，对配送效率提高、服务质量提升、配送成本降低及经济效益增加都有重要影响。配送路径的优化问题是影响物流车合理配送过程中的一个重要环节，它可以使物流配送以最低的成本、最快的响应速度、最短的运输时间，把货物运至客户手中，而后两个指标与第一个指标之间存在着一定的制约关系，无法达到总体最优，因此，这实际是一个多目标的优化问题。

进行物流配送时，物流车装载需要配送的货物从仓库出发，按事先规划好的最优配送路径为每个客户进行配送，最后返回仓库。因此，在配送之前，需要根据客户的配送地址计算出一条最优配送路径。然而，这种路径优化算法并没有考虑物流车在实际配送过程中有可能遇到诸如堵车或临时管制等异常情况。如果此时仍然按照事先规划好的路线进行配送，显然会降低配送效率。总之，现有物流配送的路径优化算法[1-11]都是静态的，不具有根据实际情况进行动态调整的功能。

因此，需要设计一个动态优化算法：一旦物流车在配送过程中出现还未经过的某路段发生堵车事件时，可以重新对物流车的配送路径进行规划，以便物流车在剩余的路径上仍是最优的。本文针对此问题进行研究并设计了一个基于回溯法的物流车动态导航算法。先利用静态回溯算法对物流车出发前进行一次静态优化，一旦物流车在配送过程中出现堵车或堵车解除，则用动态回溯算法对物流车剩余路径进行优化，使得物流车的配送效率在当前时刻总是最优的。

2 动态优化物流配送的数学模型

物流配送是一个TSP问题，给定n个站点(1个仓库和n-1个客户)间的权重ω(i,j),i,j∈{1,2,…,n}。如果ω(i,j)≠0，则物流车可以从站点i直接到达站点j；否则，物流车从站点i无法直接到达站点j，需要中转其它站点才能到达。寻找一种遍历所有站点且对每个站点仅访问一次的路径，如果总路径的权重之和最小，则称该路径为最优路径。

2.1 物流配送的静态优化模型

设G=(V,E)是赋权图，V={1,2,…,n}为站点集，E为站点间的边集，站点间的权重ω(i,j)≥0,i,j∈V，设路径Xi=sxi2…xin，其中s∈V表示物流车的始发站点(仓库)，xij∈V-{s}，j=2,…,n。且∀k≠j，有xik≠xij。则物流配送问题的数学模型表示如下：

(1)

(2)

2.2 物流配送的动态优化模型

假设物流车出发前规划好的最优路径为Xi=sxi2…xin，而在物流车行进的过程中，最优路径的某一路段xijxij+1出现堵车，则此时就需要对规划好的剩余路径进行重新优化，以便使接下来路径仍是最优的。设物流车目前正行进在xikxik+1上，则物流配送重新优化的数学模型如下：

(3)

(4)

(5)

其中X′表示剩余顶点的全排列。

3 基于回溯法的动态TSP优化算法原理

在为客户进行配送时，为了使物流车的运输成本最小，导航系统必须为物流车选择一条从仓库出发，经过要配送的每个客户一遍，最后回到仓库的路线，使物流车的总的运输成本最小。如果物流车在配送的路径上没有堵车发生，则这是一个静态的TSP优化问题。然而，在经济高速发展而交通运输压力日益加重的今天，堵车是经常发生的事情。因此，虽然物流车在出发前已经接收到导航系统的路径安排，但一旦物流车行进的路线上出现堵车事件，则要求导航系统为物流车由于避开堵车路段而需要为未配送完的客户重新选择一条最优路径。因此，要使导航系统能为物流车提供遍历客户的最短路径，则导航系统必须满足：1)物流车在出发前，导航系统根据物流车的仓库位置和配送的各客户位置以及客户间路线权重，为物流车选择一条初始的TSP优化路径；2)如果在物流车事先规划的某个路线上出现堵车，则导航系统需要对物流车未遍历的客户重新规划路径；3)如果某个路段的堵车解除，则导航系统对物流车的剩余路径需要重新优化。总之，导航系统保证物流车在当前时刻的配送路径总是最优的。

设现有1个仓库和n-1个客户，则可以对这n个位置编号为1,2,…,n。如果d(i,j)=w(i,j),∀i,j∈{1,2,…,n}，则如果d(i,j)≠0，则表示位置i和位置j之间能够相互直达。在物流车配送过程中，需要为其动态选择一个路径best_xi，i=1,2,…,n，使得物流车在当前时刻的行驶路径总是最优的。因此，令xi=i,i=1,2,…,n表示当前路径，cur_c表示回溯法的当前累加值，best_c表示当前最优值。

3.1TSP的静态回溯优化算法

在物流车出发前，需要为其规划一个最优路径。如果s是仓库所在地，则需要找到一个从s出发再回到s的最短路径。

为了使用回溯法求最优路径，首先使x1=s和xs=1，表示物流车从仓库出发。因此，需要依次搜索x2,x3,…,xn，使得(1)最小。如果x1x2…xi-1已经选定，则xixi+2…xn的选择过程如下：

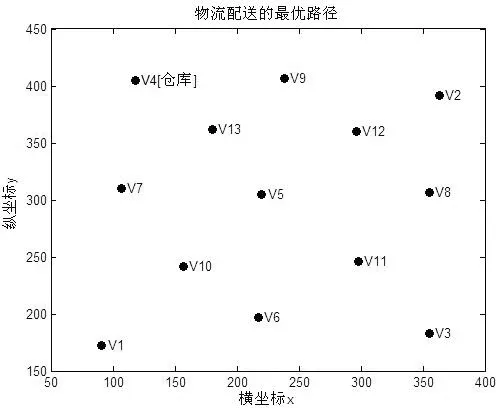
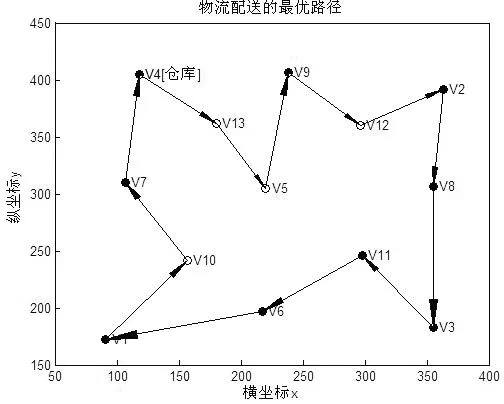
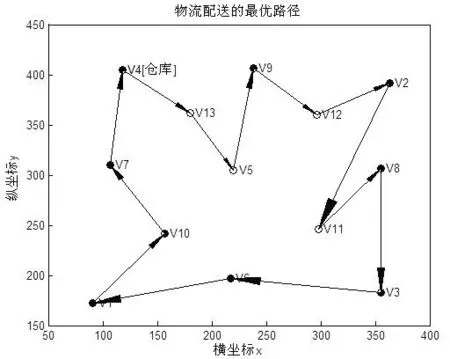
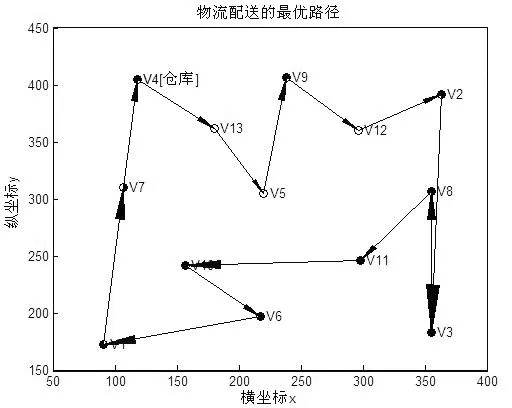
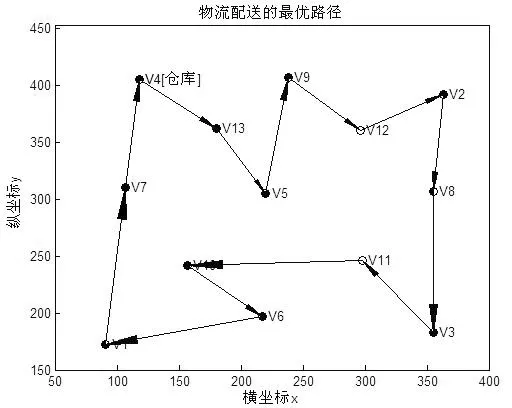
步骤1:如果i=n，d(xn-1,xn)≠0，d(xn,x1)≠0，cur_c+d(xn-1,xn)+d(xn,x1)

best_xj=xj,j=1,2,…,n。

(6)

best_c=cur_c+d(xn-1,xn)+d(xn,x1)

(7)

步骤2:如果i≠n，则从选择依次选择xj,j=i,i+1,…,n的过程如下：

(1)如果d(xi-1,xi)≠0和cur_c+d(xi-1,xj)

(2)如果j

由于x1作为仓库已经确定，故该算法是依次确定x2,x3,…,xn。

3.2 堵车时的TSP动态回溯优化算法

设当前物流车的最优路径为x1x2…xnx1，而物流车正在行驶的路段为xi-1xi，此时路段xjxj+1出现了堵车。如果路段xjxj+1出现在路径xi…xnx1中，则需要对物流车还没有配送的客户重新优化一个路径xi+1…xnx1，使得堵车前物流车已经通过的路径x1…xi和xi+1…xnx1构成堵车后的最优路径。因此，优化过程如下：

步骤1:由于路段xjxj+1堵车，为方便优化，故使

d(xj-1,xj)=d(xj,xj-1)=0

(8)

步骤2:由于物流车正在行驶的路段为xi-1xi，故需要从xi+1开始优化，以便得到一个新的xi+1…xnx1。故优化过程为：

(1)准备工作。best_c=cur_c=0，而best_xi=xi,i=1,2,…,n。

(2)从xi+1开始优化最优路径，其优化过程如算法3.1中的步骤2。

步骤3:从步骤2中可以得到新的xi+1…xnx1和best_c。由于x1…xi跟优化前一样，故

(9)

3.3 堵车解除时的TSP动态回溯优化算法

如果xi-1xi是物流车正在行驶的路段，而物流车未通过的堵车路段xjxj+1已经恢复通车。在优化之前，必须恢复堵车前路段信息，即

d(xj-1,xj)=d(xj,xj-1)=w(xj,xj+1)

(10)

至于接下来的优化过程，与算法3.2的步骤2和步骤3完全一样。

对物流车配送过程导航如下：

步骤1:物流车出发前，用算法3.1物流车规划一个最短路径。

步骤2:如果物流车配送过程中出现前方堵车，则用算法3.2对未遍历的客户点规划一个最短路径。

步骤3:如果物流车配送过程中出现两个未遍历的客户间的路段堵车解除，则用算法3.3为未遍历的客户规划一个最短路径。

步骤4:重复步骤2和步骤3，直到物流车返回仓库为止。

4 算法仿真及分析

算例 客户数据：(1)用户在软件界面上随机标注仓库与客户的地址(不少于10个客户)；(2)客户的地址表示采用Window设备坐标系。客户地址间的距离采用设备坐标像素间距模拟。动态导航要求：(1)模拟车辆从仓库出发，沿着规划的配送路线行进，最后返回仓库；(2)在配送过程中模拟前方行进路线堵车事件，软件能够绕开堵车路段动态规划配送路线。

使用VC6.0作为仿真工具，在CPU为3.2GHz和内存为1.86GB的个人台式电脑上完成仿真[12]。

在软件界面上随机选择仓库和客户的位置如图1所示。其中V4是仓库所在地，其他12个顶点是客户所在地。

图1 仓库与客户位置

图1所示顶点V1～V13的坐标依次为：(91,172)(363,392)(355,183)(118,405)(220,305)(217,197)(107,310)(355,307)(238,407) (157,242)(298,246)(296,360)(180,362)。

如果物流车在行驶的过程中未出现堵车事件，则导航系统为其规划的最优路径如图2。

图2 没有堵车的最优路径

图2中物流车的行驶路径为：V4-V13-V5-V9-V12-V2-V8-V3-V11-V6-V1-V10-V7-V4。此时最短路径的最优值为1191.27。

当物流车行驶在V5-V9路段时，路段V3-V11发生了堵车，则导航系统为物流车重新优化的路径如图3所示。

图3 路段V3-V11堵车的最优路径

图3中物流车的行驶路径为：V4-V13-V5-V9-V12-V2-V11-V8-V3-V6-V1-V10-V7-V4。此时最短路径的最优值为1308.27811。

当物流车行驶在V9-V12路段时，路段V1-V10发生了堵车，则导航系统为物流车重新优化的路径如图4所示。

图4 路段V1-V10堵车的最优路径

图4中物流车的行驶路径为：V4-V13-V5-V9-V12-V2-V3-V8-V11-V10-V6-V1-V7-V4。此时最短路径的最优值为1393.276585。

当物流车行驶在V12-V2路段时，路段V3-V11的堵车解除，而路段V1-V10的堵车保持，则导航系统为物流车重新优化的路径如图5所示。

图5 路段V3-V11堵车解除的最优路径

图5中物流车的行驶路径为：V4-V13-V5-V9-V12-V2-V8-V3-V11-V10-V6-V1-V7-V4。此时最短路径的最优值为1270.97146。

从上述导航系统对物流车的动态导航可以发现，导航系统总是使物流车在当前时刻的行驶路径是最优的。只要在物流车将要通过而未通过的路段上发生堵车，则导航系统就会为物流车余下的路线重新规划一个最短路径。同样，当某个堵车路段的堵车解除而该路段两端的客户都未遍历，则航系统也会为物流车余下的路线重新规划一个最短路径。

从导航系统为物流车进行导航的算法可知，导航系统先要为物流车进行一次静态回溯优化，而是否需要动态回溯优化取决于物流车在行驶过程中是否发生堵车事件。只有当物流车在规划的路线前方出现堵车时，导航系统才需要为物流车余下的路线进行重新规划。因此，物流车在最好的情况下，也需要进行一次静态回溯优化。静态回溯在最坏情况下可能需要更新当前最优解O((n-1)!)，每次更新最优解需O(n)，从而整个算法的时间复杂度为O(n!)。

一旦发生堵车情况，则导航系统所花费的时间就一定大于O(n!)。算法仿真发现，当n>14时，静态导航就无法满足导航的适时性要求。总之，基于回溯法的导航系统只适于n⦤14的情形。算法的优点是能够计算出物流车的最优路径而不是近似最优路径，缺点是不适合客户点较多的情形。

5 结论

针对目前的TSP算法无法解决物流车出现堵车时的最短路径问题，本文用回溯法实现了物流车的动态优化问题。该算法的优点是能够得到物流车动态导航的精确解，缺点是无法满足客户较多时的适时性要求。因此，用智能算法实现物流车的动态导航是笔者下一步研究的重点。

[1] 王胜训,李艳颖.一种求解TSP的自适应蚁群优化算法[J].西安工程大学学报,2013, 27(6):840-844.

[2] 谢曼.一种混合粒子群优化算法在TSP中的应用 [J].太原理工大学学报,2013,44(4):506-509.

[3] 贾瑞玉,李亚龙,管玉勇.求解旅行商问题的混合量子蚁群算法[J].计算机工程与应用,2013,49(22):36-39.

[4] 赵俊生.求解TSP问题的新型量子一蚁群算法[J].自动化与仪器仪表,2013,14(4):194-195.

[5] 王胜,谭家政.求解TSP问题的改进蚁群算法[J].武汉理工大学学报,2013,35(3):340-344.

[6] 李鼎,孟杰.求解TSP的改进模拟退火算法研究[J].科学技术与工程,2013,13(25):7552-7556.

[7] 柳寅,马良.模糊人工蜂群算法的旅行商问题求解[J].计算机应用研究,2013,30(9):2694-2696.

[8] 徐京雷,赵洪超,刘希玉.旅行商问题的闭环DNA算法[J].计算机工程与科学, 2014,36(1):111-114.

[9] 郭小燕,王联国,代永强.基于分段混合蛙跳算法的旅行商问题求解[J].计算机工程, 2014,40(1):191-198.

[10] 于莹莹,陈燕,李桃迎.改进的蚁群遗传算法求解旅行商问题[J].计算机仿真,2013,30(11):317-320.

[11] 尤梦丽,雷秀娟. 改进的细菌觅食算法求解TSP问题[J].广西大学学报,2013,38(6):1436-1443.

[12] 王防修,刘春红.基于哈夫曼编码的选择算法.武汉轻工大学学报,2016,35(2):79-82。

Application of backtracking in logistics vehicle dynamic navigation

WANGFang-xiu1,WANGXiao-na1,QIHua-qing2,ZHAOJie-mei1

(1.School of Mathematics and Computer Science Wuhan Polytechnic University, Wuhan 430023, China; 2.School of Economics and Management,Wuhan Polytechnic University,Wuhan 430023,China)

In this paper,dynamic navigation problem of a Logistics vehicle is researched. Because a logistics vehicle often encounters a traffic jam situation in the distribution process，so if the car still distributes in accordance with the original optimal path, it will reduce the distribution efficiency of the logistics vehicle. Traditional TSP algorithm can only supply a static optimal route for a logistics vehicle.Once the logistics vehicle is jammed in traffic,the route can’t be adjusted so that the navigation can’t improve the distribution efficiency of the logistics vehicle. To avoid this shortcoming, this paper presents a backtracking to achieve dynamic optimization distribution algorithm for the logistics vehicle. First, it uses the backtracking to achieve static optimization distribution route for the logistics vehicle and this path is regarded as the initial path of the logistics vehicle. If there is a traffic jam in the path in front of the logistics vehicle, it uses the backtracking to re-plan a new shortest path to improve the distribution efficiency for the logistics vehicle. If a section of the road is jammed and the both ends customers of the line has not been visited, it uses the backtracking to re-plan shortest path for the unvisited customers to improve the delivery efficiency. Experimental results show that the proposed algorithm can effectively improve the distribution efficiency for the logistics vehicle.

backtracking; dynamic navigation; optimal path；logistics vehicle distribution；distribution efficiency

2017-02-13.

王防修(1973-),男,副教授,E-mail:wfx323@126.com.

粮食公益性行业科研专项(201513004-3);湖北省自然科学基金项目(2016CFB273);校立大学生科研项目(xsky2016036).

2095-7386(2017)02-0073-05

10.3969/j.issn.2095-7386.2017.02.014

TP391

A