滚动轴承双谱特征提取及变工况故障诊断

张锐戈,李 劲

(1. 三明学院 机电工程学院 福建 三明 365004； 2. 装备智能福建省高校重点实验室 福建 三明 365004； 3. 湖南科技大学 信息与电气工程学院 湖南 湘潭 411201)

滚动轴承双谱特征提取及变工况故障诊断

张锐戈1，2,李 劲3

(1. 三明学院 机电工程学院 福建 三明 365004； 2. 装备智能福建省高校重点实验室 福建 三明 365004； 3. 湖南科技大学 信息与电气工程学院 湖南 湘潭 411201)

研究工况变化情形下的信号特征提取技术和轴承状态判别方法，以满足旋转装备变工况运行环境故障诊断需要。首先分析滚动轴承振动加速度信号双谱特征，发现其在不同故障类型时差异性显著，在故障相同但工况不同时又较为相似，适合提取工况鲁棒特征参数。利用双谱对称特性降低数据维数，将其划分成八个子区域后去除冗余数据，获得数据量仅为原始双谱四分之一的优选双谱。再将优选双谱做奇异值分解，依奇异值累积贡献率选择相应的左奇异向量，计算元素模值后构造特征向量。最后用连续型隐马尔可夫模型辨识故障，在轻度、中度和重度故障程度下，使用任意一种工况的数据训练诊断模型，都能有效判别四种工况的轴承状态，实现了变载荷、变转速环境的滚动轴承智能故障诊断。

故障诊断;变工况;双谱;奇异值分解;隐马尔可夫模型

1 引言

滚动轴承是旋转机械的重要部件，其状态监测和故障诊断在预防设备意外停机及降低维护成本等方面具有重要意义[1]。工程实践中，旋转机械运行工况常常发生变化，如数控机床为抑制颤振使用变转速工作模式[2]，风电设备转速及载荷随风向和风速变化[3]等。变工况情形下，滚动轴承振动特性比恒定工况时复杂，轴承状态与信号特征间的对应关系也发生变化[4]，常用的恒定工况诊断方法难以满足变工况故障诊断需要。

轴承智能故障诊断是一基于特征参量的模式识别过程。变工况故障诊断，需从工况扰动的振动信号中提取工况鲁棒特征参数，再用合适的模式识别方法辨识轴承状态。旋转机械变工况运行，主要涉及变转速、变载荷、转速和载荷同时变化三种情形，分别采用不同分析手段或特征提取策略处理信号。

变转速情形下，需消除转速变化对特征参数影响，有阶次跟踪、阶次循环平稳和阶次时频分析等方法：

(1) 阶次跟踪通过信号重采样技术，将时间域的非平稳信号转变为角度域的平稳信号，进而恢复变转速信号和转速之间的对应关系。西安交通大学Yi Wang等人先用低通滤波分离出振动信号中的转速成分，再用脊线检测技术从包络信号的短时谱中提取瞬时转速信息[5]；北京交通大学程卫东等人，研究了变转速信号等角度重采后的包络变形情况，提出修正角度变换值消除包络变形的方法[6]。

(2) 阶次循环平稳将阶次跟踪和时域平均技术相结合：能消除转速波动对振动信号影响，还通过时域平均抑制噪声和非同步周期成分[7]。印度工学院的C. Mishra等人先将振动信号进行短期角度同步平均，再结合小波去噪和包络阶次跟踪提取故障特征信息[8]。

(3) 阶次时频分析在时频域使用阶次跟踪技术，能提取非平稳信号中的瞬态时频信息。北京交通大学王天杨博士使用包络信号时频谱提取等效转频趋势线[9]；湖南大学徐亚军等人先用线性调频小波获得转速特征频率[10]，再对信号包络重采样获得角度域平稳信号；西安交通大学Ming Zhao等人将经验模态分解和包络阶次分析相结合，实现了复杂工况下的滚动轴承多损伤检测[11]。

此外，也有学者开展无需预滤波和信号重采样的变转速振动信号处理研究。加拿大渥太华大学的Juanjuan Shi等人提出一种加窗分形维数变换和广义解调的方法，克服了阶次方法的重采样误差、转频和瞬时频率耦合等问题[12]；国防科技大学范彬博士先用相空间法构建跟踪矩阵，再用平滑正交分解方法分离轴承损伤和工况变化形成的演化趋势[13]。

变载荷故障诊断通常选择载荷变化不敏感的特征值，再用合适的预处理方法提取载荷鲁棒特征参数。西安电子科技大学张锐戈博士，发现振动信号短时过零率对载荷变化不敏感，结合小波降噪实现了载荷鲁棒的滚动轴承早期故障诊断[14]；周勇等人将小波包节点能量作为特征参数，经独立特征选择后用相关向量机实现变载荷故障诊断[15]。

转速、载荷同时变化情形，需综合考虑二者变化对特征参数的扰动。华北电力大学王珊等人先用阶比重采样技术，将时间域非平稳信号转变为角度域平稳信号，再用经验模态分解方法抽取本征模态函数重构信号，实现了风电轴承转速、载荷变化情形下的早期故障诊断。华东交通大学宋京伟等人用小波包分解从振动信号时频域提取特征参量，结合连续型隐马尔可夫模型实现变载荷及未知转速下的故障诊断[17]。

电机是旋转机械的重要动力来源，滚动轴承又为电机关键零部件，工作状态会影响设备整体性能。针对电机载荷变化、转速波动运行环境，基于双谱分析提出滚动轴承变工况智能故障诊断新方法。与常用的阶次方法相比，新方法能在转速、载荷同时发生变化情形下实现变工况故障诊断，且无需进行数据重采样和转速信息提取，克服了角度域重采样误差和信号成分抽取方法的瞬时频率干扰等问题。

利用双谱分析适合处理非平稳、 非高斯随机系列，能抑制高斯噪声、分析周期重复和调制特性信号优势[18]提取信号特征。根据滚动轴承振动信号双谱在故障类型不同时差异性显著，在轴承状态相同、但工况不同时又具有一定相似性的特点，从双谱中提取工况鲁棒的特征参数。

基于双谱对称特性降低数据维数。双谱幅值分布满足y=x和y=-x对称，过中心原点将双谱划分成八个子区域后，使用两个子区域数据就能表征双谱信息。将选择的子区域进行旋转及数据合并，得到数据量仅为原始双谱四分之一的优选双谱，且降维过程运算量小于主成分分析[19]和灰度共生矩阵[20]等方法。

使用奇异值分解提取特征参数。将优选双谱做奇异值分解，依奇异值累积贡献率选择奇异向量，计算元素模值后获得故障诊断特征向量。与双谱各种切片谱[21-23]、双谱倒谱[24]、双谱能量等参数相比，奇异值分解提取特征参数具有性能稳健和抑制干扰等优点。最后用连续型隐马尔可夫模型辨识故障，凭借非平稳、高冗余及重复性低时间序列建模优势，利用观察符号可见和状态隐藏特点，从工况扰动的特征参量中判别轴承状态。

2 滚动轴承振动信号双谱

基于滚动轴承振动信号模型，推导双谱理论表征，分析轴承状态、载荷和转速等要素如何影响振动信号及其双谱。

2.1 滚动轴承振动信号模型

依据滚动轴承振动模型，当滚动体周期性通过故障部位时，可抽象成一周期性脉冲作用于轴承系统，产生的振动加速度信号可以表征为[26]：

(1)

式(1)中，T0和τi分别为冲击激励周期及其扰动，s(t)为周期性激励产生的衰减振荡，Ai为幅度调制成分，n(t)为加性噪声。s(t)和Ai分别表示为：

(2)

(3)

式(2)中fn和β分别为轴承系统的固有频率和衰减系数。式(3)中AM和AT取值由径向固有载荷和变化载荷决定，fr为转频。

若轴承状态相同、但运行工况发生变化，载荷和转速对振动信号产生下述影响：

(1) 随着轴向载荷增加，系统共振频率fn会逐渐变大，但上升幅度会逐渐减小[27]。

(2) 转速除了影响衰减振荡成分s(t)的激励周期T0，对应的转频fr还调制幅度分量Ai。

因此，滚动轴承振动信号的幅度特性受转速调制，衰减振荡成分则受载荷和转速双重因素影响。

2.2 振动信号双谱表征

将信号x(t)作零均值预处理，其三阶累积量可以表示为：

(4)

将式(1)代入式(4)，有：

(5)

计算(5)式数学期望：

C3(τ1,τ2)=

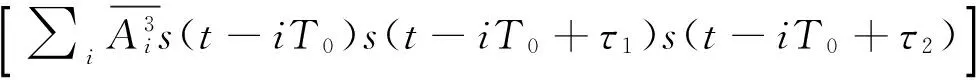
(6)

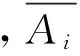
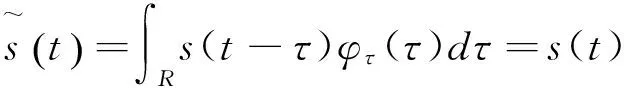
(7)

双谱定义为三阶累积量的二维傅立叶变换：

τ2)e-j2πf1τ1e-j2πf2τ2dτ1dτ2dt.

(8)

将式(6)代入式(8)，求得振动信号x(t)的双谱：

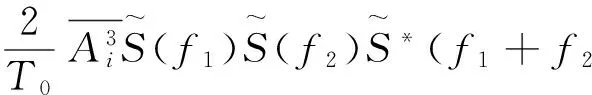
(9)

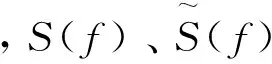
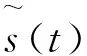
为验证上述理论推导，使用凯斯西储大学轴承研究中心数据，计算了不同故障类型、不同工况相同故障类型的振动信号双谱。其中0.355 6mm故障点直径的滚动体、内圈和外圈故障双谱如图1所示。0.533 4mm直径外圈故障，四种不同工况下的振动信号双谱如图2所示。

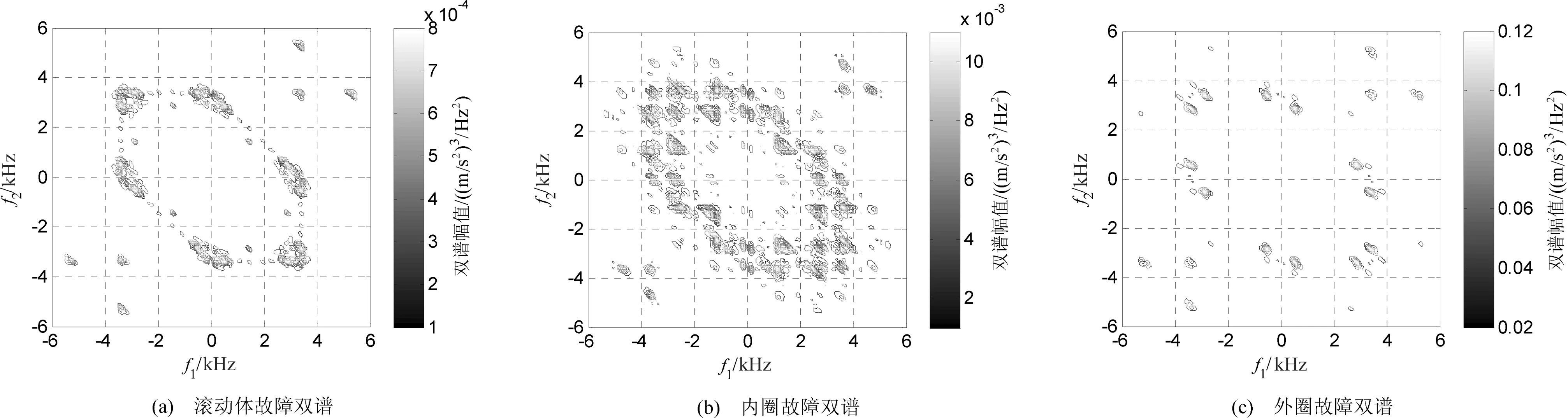
图1 不同故障状态双谱

图2 不同工况外圈故障双谱

图1和图2结果表明，不同故障状态双谱分布特性和幅值大小皆不相同，而不同工况、同种故障类型双谱的幅值大小和分布特性较为相似。亦即不同轴承状态双谱差异性显著，不同工况、相同故障状态双谱相似性显著，验证了前述理论推导结论。

3 双谱特征参数提取

3.1 基于对称特性降低双谱维数

振动信号x(t)为实序列，其傅立叶变换满足共轭对称性S(f)=S*(-f)，式(9)具有下述特征：

B(f1,f2)=B(f2,f1)=B*(-f1,-f2)=

B*(-f2,-f1).

(10)

因而双谱分布满足下述对称特性：

(11)

过双谱中心原点，依直线x=0、y=0、y=x、和y=-x，将双谱划分为如图3所示的8个子区域。

图3 双谱分布特性

式(11)和图3表明双谱幅度分布具有较大信息冗余，利用对称特性降低数据维数，步骤如下：

(3) 将区域(III)数据以原点为轴心，向右旋转90度后到达区域(I)位置，使降维后的数据具有正方性质。数据旋转通过下式完成：

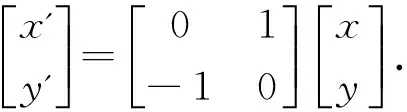
(12)

式(12)中x和y为区域(III)数据的原始坐标位置，x'和y'为旋转后的坐标位置。

图4 优选双谱

3.2 基于奇异值分解提取特征参数

将优选双谱Φ作奇异值分解：

Φ=UΣVT=

(13)

式(13)中，矩阵U和V的列分别称为左、右奇异向量，σi(i=1,…,M)为与Ui、Vi相对应的奇异值。奇异值大小能表征奇异向量重要程度，其分布特性如图5所示：

图5 奇异值分布特性

图5表明优选双谱奇异值快速减小，因而只要选择K个大奇异值对应的奇异向量，就能保留优选双谱的大部分信息并有效降低数据维数。K个奇异向量具有的信息量用奇异值累积贡献率表征[29]：

(14)

基于奇异值分解提取特征参数过程如下：

(1) 根据奇异值累积贡献率ξ，计算所需的奇异向量数目K；

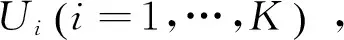
(3) 计算矩阵ψ各元素ψij的模值，作为特征参数构造M×K维特征向量O：

(15)

依上述过程得到的观察向量O，历经双谱优选和奇异值分解，继承大部分双谱信息前提下大幅度降低数据维数，实现振动信号双谱特征提取。

4 基于隐马尔可夫模型智能故障诊断

4.1 连续型隐马尔可夫模型概述[30]

将特征向量O的组成元素Oi,j作为观察符号，依聚类原理分成N类，每一个类别属于隐马尔可夫模型的一个状态，得到模型状态集S：

S={S1,S2,…,SN}.

(16)

用状态初始概率分布矩阵描述模型初始状态：

π=[π1,π2,…,πN].

(17)

元素πi表示状态的初始分布概率：

(18)

式中q0表示模型初始时刻的状态。

时间序列建模过程中，模型状态随观察向量的变化而改变，变化过程用状态转移概率矩阵描述：

(19)

aij表示模型从状态i转移到状态j的概率：

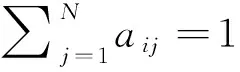
(20)

隐马尔可夫模型的转移概率aij无法直接观察，但能用观察符号概率间接表征，通过高斯混合获得：

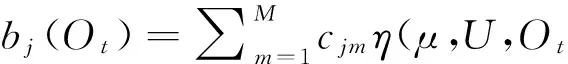
(21)

式中bj(Ot)表示t时刻观察符号Ot属于状态j的概率。η为一高斯概率密度函数，参数μ和U为混合均值矩阵和协方差矩阵，M是混合数目；cjm为混合权系数，N个状态的权系数构成混合权矩阵C。

连续型隐马尔可夫模型表示为：

λ=(A,π,C,μ,U).

(22)

实际使用时，基于可见的观察向量，使用最大期望算法确定模型参数值。

4.2 故障诊断过程描述

变工况智能故障诊断为一基于特征参数的模式识别过程，由模型训练和故障辨识两个环节构成。主要步骤如下：

(1) 提取信号特征。模型训练和故障辨识两个环节，皆需估计振动信号双谱和优选双谱，并依奇异值分解获得特征向量。

(2) 训练模型集。在模型训练阶段，先将隐马尔可夫模型参数在取值范围内随机赋值。再依当前特征向量用Baum-Welch算法[30]更新模型参数，获得当前轴承状态隐马尔可夫模型的初始分布概率、状态转移概率、混合权系数、均值矩阵和协方差矩阵。每一种工况，都计算正常状态、滚动体故障、内圈和外圈故障的隐马尔可夫模型，将其标识为λ1、λ2、λ3、λ4，形成诊断模型集。

(3) 轴承状态判别。故障辨识阶段，将任意工况、未知轴承状态获取的特征向量输入模型集，并计算不同轴承状态模型下的似然概率P(O|λi)，取值最大的模型状态被判别为待诊断的轴承状态。

为保证故障诊断有效性，模型训练和故障辨识两个环节数据没有重叠。具体流程如图6所示。

图6 基于隐马尔可夫模型的变工况智能故障诊断

5 实验研究

5.1 数据描述

研究对象为安装于电机驱动端的6205-2RS轴承，通过调节测功机扭矩和电机转速模拟运行工况，详情如表1所示。

表1 工况参数

工况载荷/kW转速/(r/min)工况101797工况20.7351772工况31.4711750工况42.2061730

用电火花加工点蚀故障模拟不同的故障类型。每一类故障，都加工深度为0.279 4mm，直径分别为0.177 8mm，0.355 6mm和0.533 4mm的故障点，来表征不同的故障程度。数据由凯斯西储大学轴承研究中心采集，加速度传感器用磁力吸座安装于轴承座正上方，信号采样频率为12kHz。每一类故障程度，皆有4种工况、4种轴承状态振动加速度信号用于变工况故障诊断研究。

5.2 参数设置

(1) 双谱计算。用直接法估计，序列长度取1 024数据点，数据片段取256点、75%重复度，频域用宽度为5的Rao-Gabr窗平滑。

(2) 奇异向量数目选择。奇异值累积贡献率ξ在0.177 8mm故障时设为50%，0.355 6mm故障时为80%，0.533 4故障时为85%，对应的奇异向量个数分别取4，16和12。

(3) 模型训练。隐马尔可夫模型的状态和混合个数设为2，参数估计的收敛门限值及最大迭代次数分别设为0.001和50。

5.3 实验结果

实验依故障程度不同分3组进行。每组实验中，先训练不同工况的隐马尔可夫模型集，再用其辨识任意工况轴承状态。模型训练和故障辨识使用不同数据以保证诊断有效性，每种状态用1 000组数据验证诊断效果，正确识别的数据组数与输入数据组数间的比值称为辨识精度。三种故障程度诊断结果见表2、表3和表4，表中最左列表示待辨识数据，后面4列表示不同工况诊断模型的辨识结果，详情如表2—表4所示。

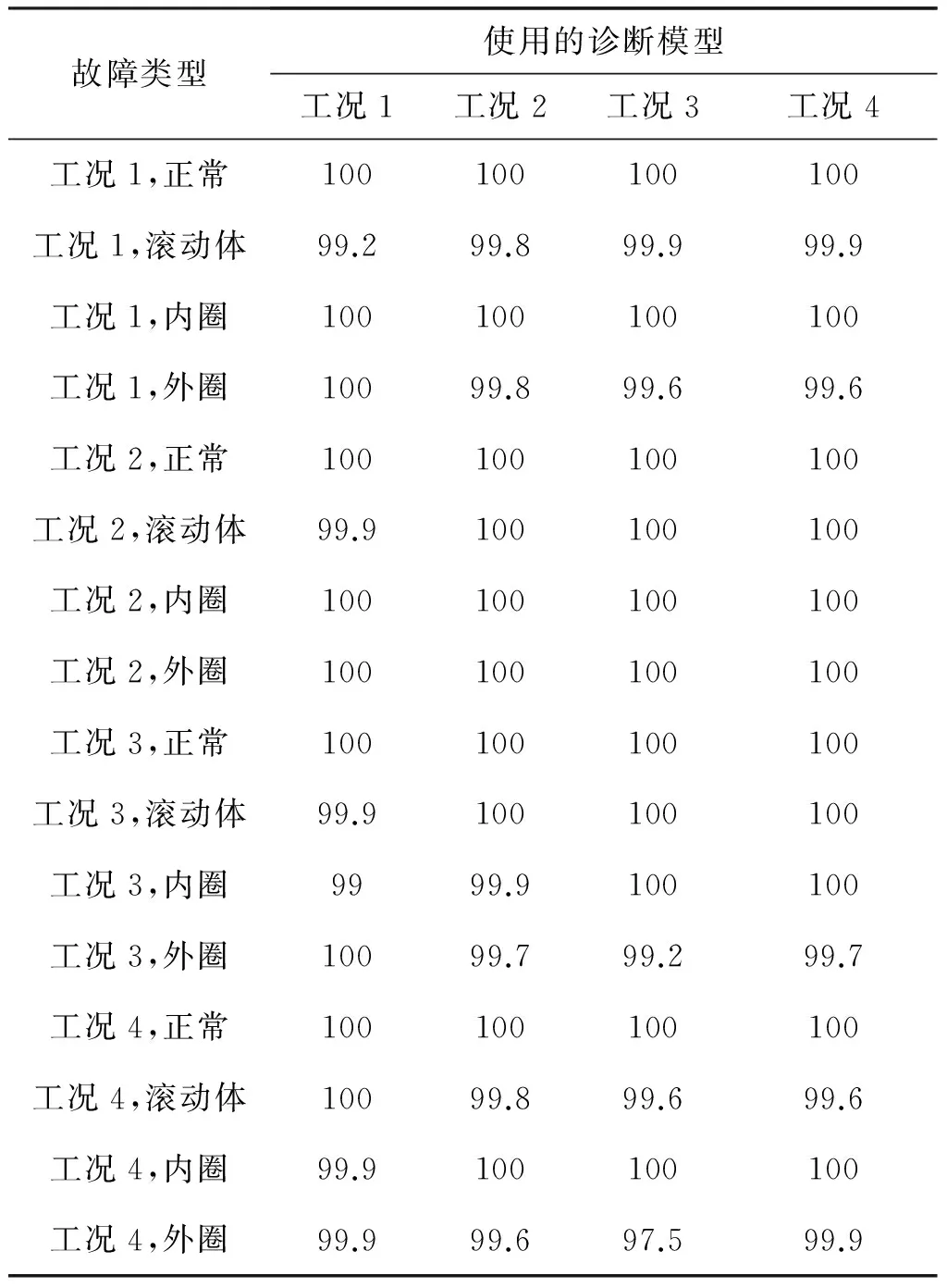
表2 0.177 8 mm故障程度辨识精度 /%

表3 0.355 6mm故障程度辨识精度 /%

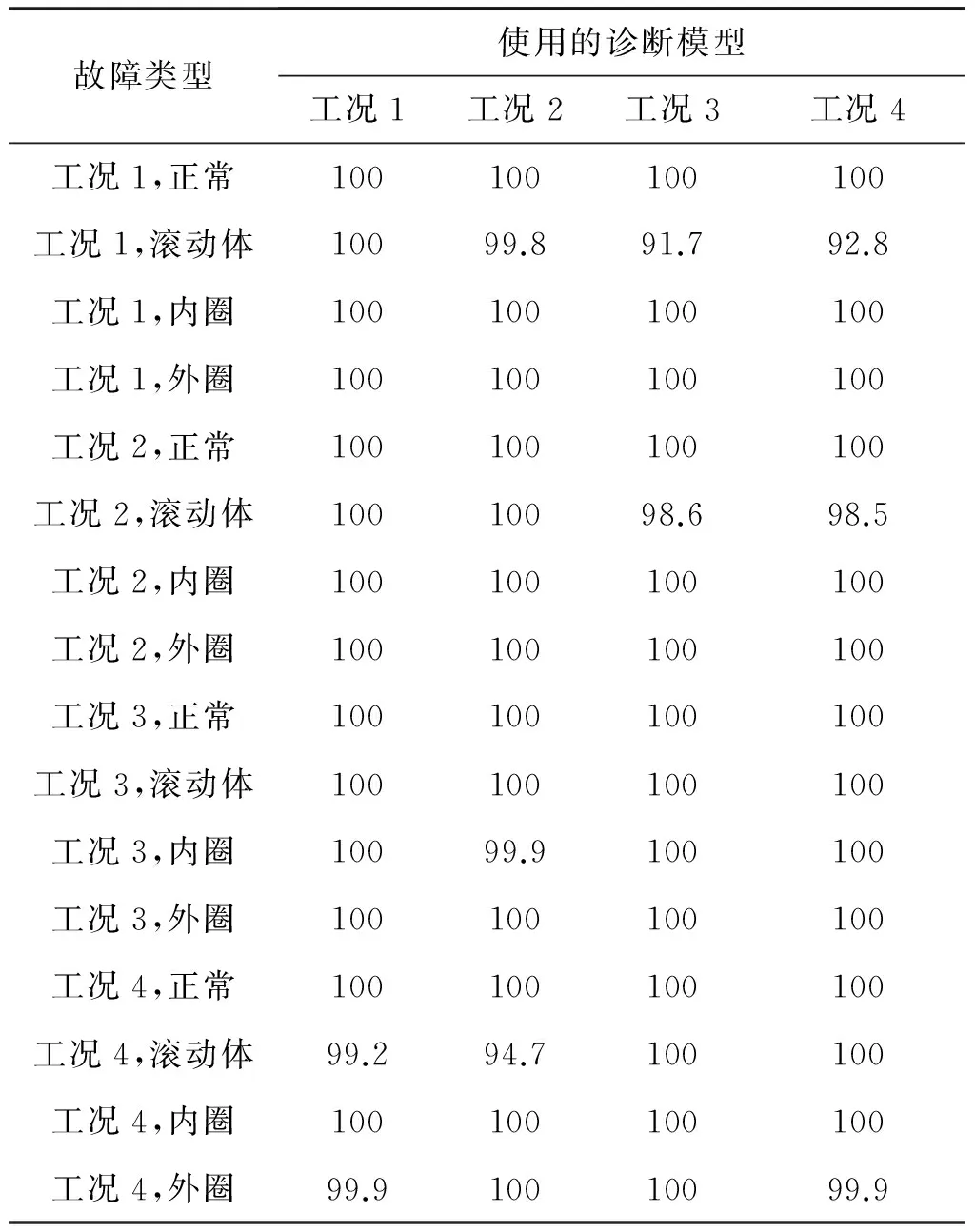
表4 0.533 4mm故障程度辨识精度 /%

5.4 实验分析

实验结果表明，在三种不同的故障程度下，使用任意一种工况数据训练诊断模型，都能正确辨识四种工况的轴承状态。即诊断方法克服了转速和载荷变化对特征参量的扰动，是一种适应工况变化的鲁棒诊断方法。与当前常用的阶次方法相比，文中方法无需数据重采样，也不要提取设备转速信息，是一种稳健、高效的智能故障诊断方法。

表2、表3和表4的诊断结果有下述特点：

(1) 不同故障程度的辨识精度存在差异。如表2中辨识精度皆大于99%，而表3和表4的辨识精度在某些轴承状态下稍低一些。其原因是不同故障程度时产生的周期性激励不一致，而某些情形的激励使双谱产生较大扰动影响模型辨识精度。

(2) 训练数据与辨识数据间的工况差异程度影响辨识精度。如表3中工况1模型对工况4的内圈故障诊断，表3中工况4模型对工况1和工况2的滚动体故障诊断，以及表4中工况4模型对工况1的滚动体故障诊断，辨识精度要比工况接近时低一些。其原因是双谱特征受工况差异程度影响，工况接近时双谱较为相似，反之则差异较大。图7(a)和图7(b)为表3中工况1和工况2的优选双谱，其幅度和分布特性比较接近。图7(c)为表3中工况4优选双谱，其幅度和分布特性与前两种工况差别较大。双谱差异导致特征参数扰动，干扰隐马尔可夫模型似然概率估值并影响轴承状态辨识。

图7 三种工况内圈故障优选双谱，0.355 6 mm故障点直径

5.5 诊断方法可适性验证

本节对另一型号、不同使用环境滚动轴承开展变工况故障诊断，以验证诊断方法的普适性。轴承型号为6203-2RS，安装于电机风扇端，用电火花加工点蚀故障模拟不同故障类型，用不同直径故障点模拟不同故障程度。安装时将外圈故障点置于6点钟位置，电机的转速和载荷数据与表1相同，故障点直径与4.1节的6205-2RS轴承相同。数据由凯斯西储大学轴承研究中心提供，0.177 8mm和0.355 6mm故障点直径时包含四种运行工况数据，0.533 4mm故障点直径时包含工况2、工况3和工况4的数据。

三种故障程度的奇异向量数目分别为12、24和12，双谱估计、隐马尔可夫模型训练参数与4.2节一致，辨识精度用1 000组数据计算。6203-2RS轴承的辨识精度表明诊断方法具有较好的适用性，详见表5、表6和表7。

表5 6203-2RS轴承0.177 8mm故障程度辨识精度/%

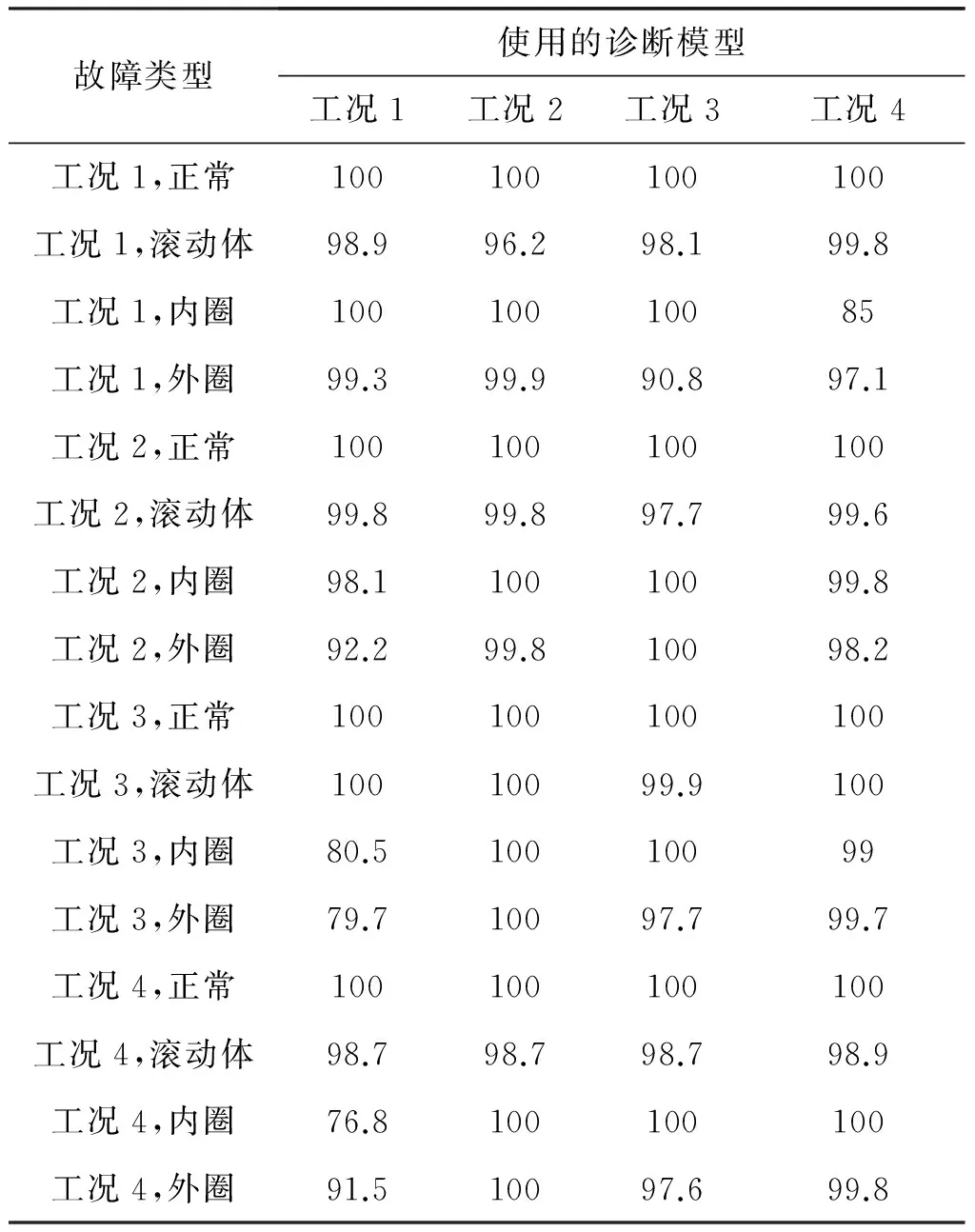
故障类型使用的诊断模型工况1工况2工况3工况4工况1,正常100100100100工况1,滚动体98.996.298.199.8工况1,内圈10010010085工况1,外圈99.399.990.897.1工况2,正常100100100100工况2,滚动体99.899.897.799.6工况2,内圈98.110010099.8工况2,外圈92.299.810098.2工况3,正常100100100100工况3,滚动体10010099.9100工况3,内圈80.510010099工况3,外圈79.710097.799.7工况4,正常100100100100工况4,滚动体98.798.798.798.9工况4,内圈76.8100100100工况4,外圈91.510097.699.8

表6 6203-2RS轴承0.355 6mm故障程度辨识精度/%

故障类型使用的诊断模型工况1工况2工况3工况4工况1,正常100100100100工况1,滚动体96.684.392.698.8工况1,内圈100100100100工况1,外圈10010098.2100工况2,正常100100100100工况2,滚动体96.883.49899.9工况2,内圈100100100100工况2,外圈100100100100工况3,正常100100100100工况3,滚动体75.578.3100100工况3,内圈100100100100工况3,外圈100100100100工况4,正常100100100100工况4,滚动体8375.6100100工况4,内圈98.9100100100工况4,外圈100100100100

表7 6203-2RS轴承0.533 4mm故障程度辨识精度/%

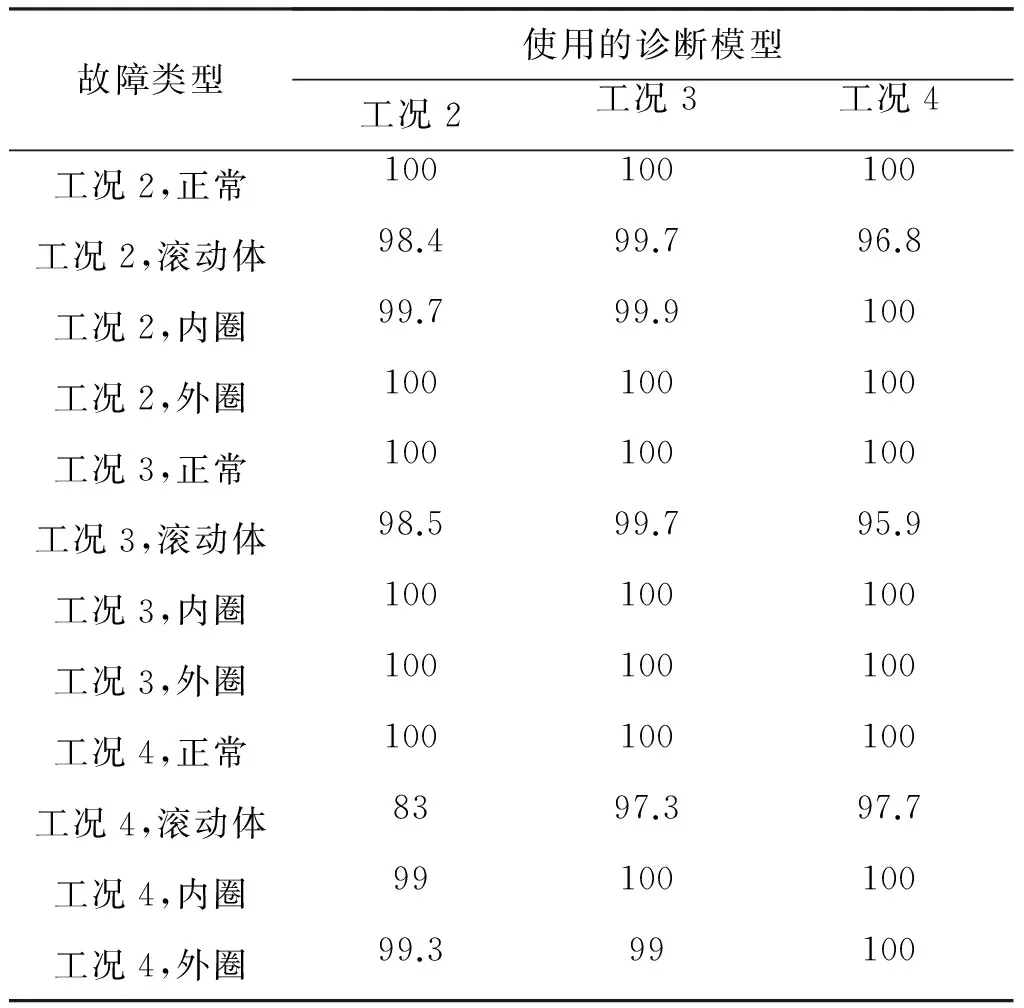
故障类型使用的诊断模型工况2工况3工况4工况2,正常100100100工况2,滚动体98.499.796.8工况2,内圈99.799.9100工况2,外圈100100100工况3,正常100100100工况3,滚动体98.599.795.9工况3,内圈100100100工况3,外圈100100100工况4,正常100100100工况4,滚动体8397.397.7工况4,内圈99100100工况4,外圈99.399100

6 结论

(1) 双谱能有效表征变工况情形的滚动轴承状态，故障类型不同时具有显著差异性，故障相同但工况不同时又具有较高相似性；滚动轴承振动信号双谱具有较大信息冗余，基于对称特性剔除冗余数据能大幅度降低数据维数。

(2) 奇异值分解是一种有效的特征提取方法，经奇异值累积贡献率选择奇异向量，能获得可靠的特征信息并降低数据维数。

(3) 隐马尔可夫模型是一种稳健的时间序列建模工具，能适应轴承运行工况变化引起的观察向量扰动，并依据可见的特征参数辨识隐藏的故障状态；使用期望最大算法计算隐马尔可夫模型参数，训练过程存在收敛于局部最优值情形，最优的隐马尔可夫模型初始参数选择还有待于进一步研究。

[1]El-ThaljiI,JantunenE.Asummaryoffaultmodellingandpredictivehealthmonitoringofrollingelementbearings[J].MechanicalSystemsandSignalProcessing, 2015, 60-61: 252-272.

[2] 李勤良，汪博，赵斌，等. 考虑非线性迟滞力的机床颤振系统稳定性研究[J]. 机械工程学报, 2013(11): 43-49.

[3]VillaLF,ReonesA,PeránJR,etal.Angularresamplingforvibrationanalysisinwindturbinesundernon-linearspeedfluctuation[J].MechanicalSystemsandSignalProcessing, 2011, 25(6): 2157-2168.

[4] 林京，赵明. 变转速下机械设备动态信号分析方法的回顾与展望[J]. 中国科学:技术科学, 2015(7): 669-686.

[5]WangY,XuG,ZhangQ,etal.Rotatingspeedisolationanditsapplicationtorollingelementbearingfaultdiagnosisunderlargespeedvariationconditions[J].JournalofSoundandVibration, 2015, 348: 381-396.

[6] 程卫东，王天杨，WangJin-jiang，等. 包络变形对阶比分析结果的影响及消除方法[J]. 振动工程学报, 2015(3): 470-477.

[7]WangT,LiangM,LiJ,etal.Bearingfaultdiagnosisunderunknownvariablespeedviagearnoisecancellationandrotationalordersidebandidentification[J].MechanicalSystemsandSignalProcessing, 2015, 62-63: 30-53.

[8]MishraC,SamantarayAK,ChakrabortyG.Rollingelementbearingdefectdiagnosisundervariablespeedoperationthroughanglesynchronousaveragingofwaveletde-noisedestimate[J].MechanicalSystemsandSignalProcessing, 2016, 72-73: 206-222.

[9] 王天杨，李建勇，程卫东. 基于低次故障特征阶比系数的变转速滚动轴承等效转频估计算法[J]. 机械工程学报, 2015(3): 121-128.

[10] 徐亚军，于德介，孙云嵩，等. 滚动轴承故障诊断的阶比多尺度形态学解调方法[J]. 振动工程学报, 2013(2): 252-259.

[11]MingZ,JingL,XiaoqiangX.Multi-FaultDetectionofRollingElementBearingsunderHarshWorkingConditionUsingIMF-BasedAdaptiveEnvelopeOrderAnalysis[J].Sensors, 2014, 14(11): 20320-20346.

[12]ShiJ,LiangM,GuanY.Bearingfaultdiagnosisundervariablerotationalspeedviathejointapplicationofwindowedfractaldimensiontransformandgeneralizeddemodulation:Amethodfreefromprefilteringandresampling[J].MechanicalSystemsandSignalProcessing, 2016, 68-69: 15-33.

[13] 范彬，胡雷，胡茑庆. 变工况下旋转机械故障跟踪的相空间曲变方法[J]. 物理学报, 2013(16): 63-70.

[14]WanX,WangD,TsePW,etal.Acriticalstudyofdifferentdimensionalityreductionmethodsforgearcrackdegradationassessmentunderdifferentoperatingconditions[J].Measurement, 2016, 78: 138-150.

[15] 周勇，何创新. 基于独立特征选择与相关向量机的变载荷轴承故障诊断[J]. 振动与冲击,2012(3): 157-161.

[16] 王珊，苏璐玮，顾煜炯，等. 变工况特性下的风电轴承早期故障诊断方法[J]. 电力科学与工程,2014(03): 39-44.

[17] 宋京伟，梅秀庄，郭云. 变转速变载荷下滚动轴承故障的小波-HMM诊断[J]. 轴承，2005(12): 28-32.

[18]DongG,ChenJ,ZhaoF.Afrequency-shiftedbispectrumforrollingelementbearingdiagnosis[J].JournalofSoundandVibration. 2015, 339: 396-418.

[19] 张锐戈，谭永红. 双谱主成分分析的滚动轴承智能故障诊断[J]. 振动工程学报，2014(05): 763-769.

[20] 林勇，胡夏夏，朱根兴，等. 基于振动谱图像识别的智能故障诊断[J]. 振动、测试与诊断，2010, 30(2): 175-180.

[21]ZhouY,ChenJ,DongGM,etal.Applicationofthehorizontalsliceofcyclicbispectruminrollingelementbearingsdiagnosis[J].MechanicalSystemsandSignalProcessing. 2012, 26(0): 229-243.

[22] 张琳，黄敏. 基于EMD与切片双谱的轴承故障诊断方法[J]. 北京航空航天大学学报，2010(3): 287-290.

[23] 周宇，陈进，董广明，等. 基于循环双谱的滚动轴承故障诊断[J]. 振动与冲击. 2012, 31(09): 78-81.

[24] 李辉，郑海起，唐力伟. 基于倒双谱分析的轴承故障诊断研究[J]. 振动、测试与诊断，2010, 30(4): 353-356.

[25] 黄晋英，潘宏侠，毕世华，等. 基于高阶累量谱的轴承故障诊断[J]. 火炮发射与控制学报，2007(2): 56-59.

[26] Cong F, Chen J, Dong G, et al. Vibration model of rolling element bearings in a rotor-bearing system for fault diagnosis[J]. Journal of Sound and Vibration. 2013, 332(8): 2081-2097.

[27] 赵联春，马家驹，马纯青. 载荷对球轴承振动特性的影响[J]. 轴承，2003(05): 38-41.

[28] Yang D M, Stronach A F, Macconnell P, et al. Third-order spectral techniques for the diagnosis of motor bearing condition using artificial neural netwroks[J]. Mechanical Systems and Signal Processing. 2002, 16(2-3): 391-411.

[29] He Q, Yan R, Kong F, et al. Machine condition monitoring using principal component representations[J]. Mechanical Systems and Signal Processing. 2009, 23(2): 446-466.

[30] Rabiner L R. A tutorial on hidden Markov models and selected applications in speech recognition[J]. Readings in speech recognition. 1990, 53(3): 267-296.

Fault diagnosis of variety operation conditions for rolling element bearings based on bispectrum feature extraction

ZHANGRui-ge1,2,LIJing3

(1. College of Mechanical and Electronic Engineering, Sanming University, Sanming 365004,China; 2. Key Laboratory of Intelligent Equipment of Fujian Province Universities, Sanming 365004,China; 3. School of Information and Electrical Engineering, Hunan University of Science and Technology, Xiangtan 411201,China)

This paper presents a novel method for the feature extraction and bearing status identification under the varying loads and rotation speed, which can be applied in the fault diagnosis of the rotating equipment of variety operation conditions. Firstly, we explored the bispectrum of the vibration acceleration signals, and found the bispectrum distribution was of significant differences under different bearing status, but very similar to the same fault type under different operation conditions. Thus, it is appropriate to extract the robust features from the bispectrum for the fault diagnosis of variety operation conditions. Then, the bispectrum was divided into eight sub-zones according to the symmetric characteristics. After the redundant data were removed, the retained data were called the preferred bispectrum, which only had a quarter data of the original bispectrum. The feature extraction applied the singular value decomposition, the number of the singular vectors was also determined by the accumulated contribution rate by the singular value, and the modulus of the selected singular vectors was as the features. Finally, we conducted a number of experiments under four operation conditions of three fault severities to validate the efficiency of the proposed method. The results show that the proposed method effectively identify various fault types and is robust to the varying operating conditions.

fault diagnosis;variety operation conditions;bispectrum;singular value decomposition;Hidden Markov model

2017-05-02.

张锐戈(1977-)，男，博士，副教授，E-mail:ruig_zhang@126.com.

国家自然科学基金资助项目(61474042)；福建省科技厅重点项目(2013N0032).

2095-7386(2017)02-0057-10

10.3969/j.issn.2095-7386.2017.02.012

TN 911.6;TP 206.3

A