钢弹簧浮置板阻尼比试验研究

宋姣姣，高志升，练松良

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.安境迩（上海）科技有限公司，上海 200030）

钢弹簧浮置板阻尼比试验研究

宋姣姣1，高志升2，练松良1

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.安境迩（上海）科技有限公司，上海 200030）

阻尼比是评价结构减振效果的重要指标，也是轨道结构动力仿真的关键参数。为了对普通钢弹簧浮置板的阻尼比进行测试分析，对比了落轴和循环加载两种阻尼比测试结果，并探究了不同固有频率计算方法和循环加载次数对系统整体阻尼比的影响。测试结果表明，落轴试验中使用功率谱法或公式法进行结构固有频率计算对最终阻尼比结果影响不大；疲劳试验中经过235万次加载后，钢弹簧浮置板的阻尼比下降15.48%；采用落轴或循环加载测试的各次阻尼比试验结果一致性较好。

轨道交通；钢弹簧浮置板；对数衰减法；滞回曲线

浮置板轨道结构是解决轨道交通振动和噪声问题的最有效方法，浮置板的阻尼比是影响钢弹簧浮置板系统减振降噪效果的重要因素。阻尼比是阻尼系数与临界阻尼的比值[1]，是结构动力学中表征结构阻尼大小的指标，通常采用落轴或者力锤等冲击产生的自由振动试验来测定阻尼比大小[2-4]，循环加载(疲劳试验)应用较少。本文采用落轴和循环加载两种试验方法计算钢弹簧浮置板的阻尼比，并对测试结果进行了对比分析。在落轴试验中，探究了功率谱法、公式法两种固有频率计算方法对图形滤波和最终阻尼比的影响；在疲劳试验中，使用结构实时动刚度计算系统固有频率，并分析了加载次数对钢弹簧浮置板整体阻尼比的影响。

1 测试原理

通过荷载作用下振动质量的位移计算阻尼比的理论方法，主要有对数衰减率法[5]，共振放大法[6]和半功率点法[7]。本文采用落轴和循环加载两种方法测算阻尼比，其对应的计算原理分别为对数衰减法和滞回曲线法[1,8-9]。

1.1 对数衰减率法[1]

对数衰减法计算阻尼比的基本思想是阻尼比控制自由振动衰减的速度，根据这一原理，定义相隔n周的峰值比的自然对数值为对数衰减率λ：

图1显示了某次落轴试验测得的浮置板自由振动波形。用对数衰减法进行阻尼比计算时，不同的n取值会对计算结果造成一定的影响[10]。经验表明，当取合适的n值使得对应位置处的波峰幅值Xi+n小于Xi的50%[1]时，可以保证计算结果的准确性。本次试验中，当周期间隔为3时，浮置板自由振动衰减波形均可满足X4小于X1的一半，因此，本文计算对数衰减率时n取值为3。

根据有阻尼自由振动解式推导出来的对数衰减率与阻尼比的关系，可得结构阻尼比ξ的计算公式（2）[1]：

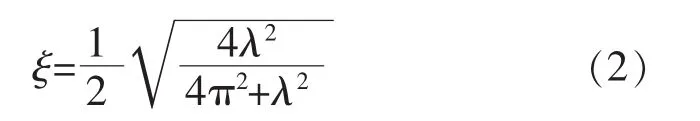
1.2 滞回曲线法[1]

描述力与位移之间关系的曲线称为滞回曲线，每个封闭的滞回环代表一次完整的加载振动周期。基于能量等效的原则，易知一个振动循环内实际阻尼做的功等于实测荷载做的功，即图2（a）阻尼力滞回环的面积与图2（b）荷载滞回环的面积相等。

图1 相邻振动峰值的定义Fig.1 Definition of adjacent vibration amplitude peak

图2 滞回曲线Fig.2 Hysteresis curve

因此有：

2 试验测试

代入c=2mξωn，变换形式可求得阻尼比计算公式（4），式中ωn为系统固有频率。

2.1 试验材料及设备

测试对象为普通预制单块钢弹簧隔振器浮置板，板长3.6 m，板下均布6个隔振器，单个隔振器的名义静刚度为6.60 kN/mm。试验所用的主要仪器和测试设备见表1。其中，疲劳试验机的加载频率为每分钟200次。

2.2 测试方案

轨道结构架设完毕后，先进行落轴试验，现场测试如图3所示。在图3（a）板中布置W1和W2两个位移传感器，采集浮置板垂向位移数据，落轴冲击作用面为左图中虚线所示板中位置，试验开始后进行高度为10 mm和20 mm的落轴试验各5次；随后进行循环加载试验，在右图中加载点安装测力传感器，位移测点W1～W6布置在中对应位置，测试开始后，采集加载0万次和235万次时各测点的垂向位移和作用力15 min。

表1 主要试验仪器和设备Tab.1 Main test instruments and equipment

图3 阻尼比试验测点布置图Fig.3 Points arrangement in damping ratio tests

3 数据分析

3.1 落轴试验数据分析

由于试验装置的各种模态振动，还有环境振动，所以在结构第一振动基频信号上还有较多的其他频率的信号参杂其中，导致位移信号幅值失真，因此需要对测得的位移信号进行滤波，以排除其他信号的干扰。本文试验时，假定整个浮置板系统是单自由度系统，故可利用结构的固有频率设置滤波范围，为此需要先确定结构的固有频率。

本文分别采用功率谱法和公式法两种方法计算结构固有频率：

1）公式法：板的振动固有频率计算公式如式（5）：

式中：f为固有频率，Hz；k为系统垂向刚度，N/m；m为系统质量，kg。

测得该钢弹簧浮置板系统的整体静刚度为39.96 kN/mm，板的总质量约为8 800 kg，则可得该钢弹簧浮置板系统的固有频率为10.72 Hz。

2）功率谱法：认为本次测试中5 Hz以下的信号来源于试验装置及场地周边环境的振动干扰，数据标定后，先对自由振动波形进行5 Hz高通滤波，滤去该部分低频干扰信号，然后对滤波后的信号进行功率谱分析[11]（图4），得到该钢弹簧浮置板在落轴时的自由振动频率为12.7 Hz。

以固有频率上下各10%为界进行带通滤波，得到滤波后的位移信号波形，如图5所示。发现自由振动初期采用12.7 Hz滤波的振幅略大于10.72 Hz，随着振动的衰减，两种滤波波形基本重合。

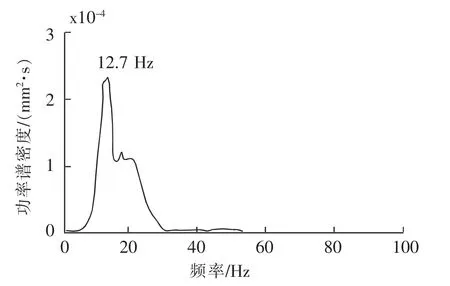
图4 垂向位移功率谱密度Fig.4 Power spectral density of vertical displacement

图5 滤波前后垂向位移波形图Fig.5 Vertical displacement wave before and after filtering

3.2 循环加载试验数据分析

在疲劳试验中，对原始数据进行标定，可得到如图6所示的系统荷载和浮置板垂向位移值，使用MATLAB程序将荷载和位移曲线截取成n个完整的一一对应的波动周期，记为Ni（i=1，2，3，···，n）。根据第一节中所述原理，以位移为横坐标，荷载为纵坐标，可得到n个滞回曲线，每个滞回曲线的面积代表该周期内阻尼力做功所消耗的能量。

图6 时间-荷载、时间-垂向位移曲线Fig.6 Time-load and time-vertical displacement wave

图7 实测荷载滞回曲线Fig.7 Measured load hysteresis curve

以测点4处的22个荷载-位移滞回曲线为例，对比分析加载0万次和235万次时荷载回曲线的变化。从图7中可以看出，经过235万次加载后，钢弹簧浮置板的滞回曲线变得更加狭长，系统荷载仍为40～180 kN，但系统垂向位移最大值明显增大，浮置板垂向位移区间长度明显增加，这一现象尚需进一步的研究。

运用公式（4）进行疲劳荷载阻尼比计算，首先需要计算系统的固有频率。钢弹簧浮置板的总体质量为7 900 kg，加载0万次时，系统垂向动刚度为36.19 kN/mm，加载235万次后，系统垂向动刚度下降至26.35 kN/mm。根据公式（5）计算可得钢弹簧浮置板加载0万次时的固有频率为10.77 Hz，加载235万次后的固有频率为9.19 Hz。

4 试验结果及分析

4.1 落轴试验阻尼比

使用两种固有频率滤波后的波形进行阻尼比计算，得到不同落轴高度下单块钢弹簧浮置板的整体阻尼比，计算结果见表2。

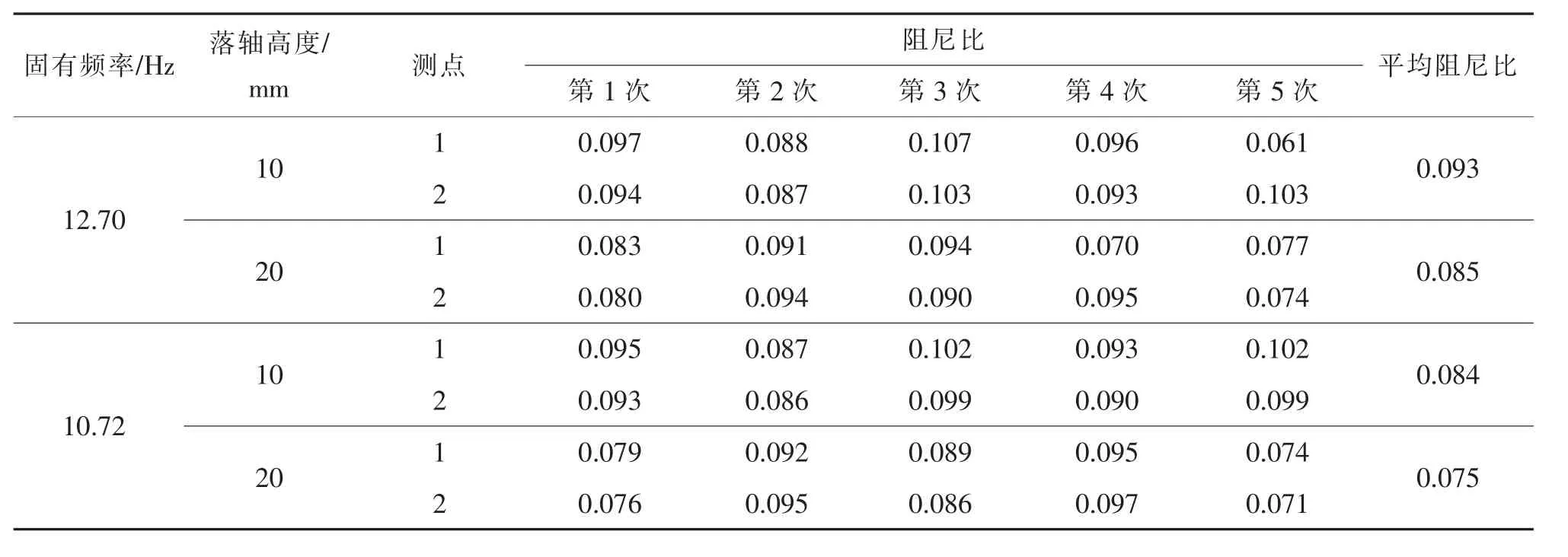
表2 钢弹簧浮置板整体阻尼比（落轴）Tab.2 Integral damping ratio of steel spring floating slab(wheel-set dropping test)

落轴测试结果显示，采用测试信号的功率谱计算所得12.7 Hz作为结构固有频率计算所得的钢弹簧浮置板阻尼比在10 mm和20 mm的落轴高度下分别为0.093和0.085；使用公式法计算所得的10.72 Hz作为结构固有频率计算所得的系统阻尼比在10 mm和20 mm的落轴高度下分别为0.084和0.075。两种落轴高度时使用功率谱法计算的阻尼比结果与公式法相比分别偏大0.008和0.01，对应误差分别为10.71%和13.33%，总体来说，在对数衰减法中，使用功率谱法或者公式法计算结构固有频率，对钢弹簧浮置板的阻尼比测试结果影响不大。

4.2 循环加载试验阻尼比

根据第一节中所述的滞回曲线法，分别使用加载0万次和235万次时对应的固有频率计算该状态下的钢弹簧浮置板整体阻尼比，得到各测点的阻尼比及其均值如表3所示。

表3 钢弹簧浮置板整体阻尼比（疲劳）Tab.3 Integral damping ratio of steel spring floating slab(circle loading test)

以6个测点的阻尼比平均值作为钢弹簧浮置板的整体阻尼比，对疲劳试验前后的系统阻尼比进行对比分析。可以发现，加载235万次后，钢弹簧浮置板的整体阻尼比下降了0.013，降幅为15.48%。

4.3 不同测试方法对比分析

对比分析图8中采用落轴与循环加载两种不同试验方法的测试结果，发现采用不同试验方法测得的单块浮置板阻尼比结果相近：疲劳试验加载0万次的阻尼比与各次落轴试验测试结果的分别相差-9.68%，-1.18%，0%，12%；加载235万次后与各次落轴试验测试结果的分别相差-23.66%，-19.72%，15.48%，5.33%。在两种不同固有频率的落轴试验中，疲劳试验阻尼比的测试结果与结构固有频率取10.72 Hz时的落轴试验结果更相近，说明与使用功率谱法相比，采用公式法计算固有频率能使对数衰减法的阻尼比测试结果与滞回曲线法一致性更好。

图8 不同试验方法阻尼比测试结果Fig.8 Damping ratios obtained by various test methods

5 结论

1）落轴试验中，本文分析了不同固有频率计算方法对阻尼比测试结果的影响。结果表明，使用功率谱法或者公式法进行固有频率计算，对最终阻尼比的测试结果影响不大，两种落轴高度时使用功率谱法计算的阻尼比结果与公式法相比分别偏大0.008和0.01，分别相差10.71%和13.33%

2）循环加载试验中，经过235万次加载后，滞回曲线变得更加狭长，浮置板垂向位移明显增加，但系统荷载无明显变化。阻尼比在经过235万次疲劳荷载后下降了0.013，降幅为15.48%。

3）本试验测试和计算结果表明，采用落轴或循环加载试验对单块钢弹簧浮置板阻尼比的测试结果没有明显影响，两种试验方法各次阻尼比误差均在25%以内，且与使用功率谱法相比，采用公式法计算固有频率能使落轴试验的阻尼比测试结果与疲劳试验一致性更好。

参考文献：

[1]刘晶波.结构动力学[M].北京：机械工业出版社，2007：46-65.

[2]刘卫星，王午生.铁路碎石道床动刚度与阻尼的试验研究[J].铁道学报，2002（6）：99-104.

[3]薛弼一，王谛，肖新标，等.辐板屏蔽式阻尼车轮振动声辐射特性试验研究[J].机械工程学报，2013（10）：1-7.

[4]YASHIHIKO SATO.轨道弹簧常数和衰减系数的测定[C]//铁道部重大基础性研究项目“轨道结构刚度合理值及其合理匹配的研究”资料集，北京：铁道科学研究院，1999：156-162.

[5]柳志远，刘鹏郎，易理，等.橡胶式扭振减振器固有频率与阻尼比的测试方法比较[J].北京农业工程大学学报，1995（4）：13-17.

[6]贺亮，周永清，朱思洪.基于激振法的空气弹簧垂向刚度和阻尼特性研究[J].振动与冲击，2008（7）：167-170+195.

[7]陈奎孚，焦群英.半功率点法估计阻尼比的误差分析[J].机械强度，2002（4）：510-514.

[8]罗飞，何依婷，赵淑萍，等.分级加载下冻土阻尼比的试验研究[J].岩土力学，2015（11）：3143-3149.

[9]金建敏，谭平，周福霖，等.天然橡胶支座(LNR)的等效阻尼比试验研究[J].西安建筑科技大学学报：自然科学版，2009（5）：663-667.

[10]王金，李玉路，邵文杰，等.基于自由振动的钢弹簧浮置板阻尼比测试分析[J].华东交通大学学报，2015（5）：1-5.

[11]李蓓蓓.振动分析的有效工具——功率谱密度[J].包装工程，2004（3）：46-47+50.

Test and Research of Damping Ratio for Steel Spring Floating Slab

Song Jiaojiao1，Gao Zhisheng2，Lian Songliang1
（1.Key Laboratory of Road and Traffic Engineering of the Ministry of Education，Tongji University，Shanghai 201804，China；2.AnJing Er(Shanghai)Technology Co.，LTD.，Shanghai 200030，China）

Damping ratio is an essential index in structure vibration evaluation as well as one of the key parameters in dynamic simulation.In order to test damping ratio in a typical steel spring floating slab，this paper compared damping ratio results calculated by two kinds of different tests，the wheel-set dropping test and the circle loading test.Effects of various inherent frequency calculating methods and different circle loading times on the whole damping ratio were also analyzed.The results showed that in wheel-set dropping test damping ratios are basically the same when involving various inherent frequencies calculated via either power spectral density or formula;in circle loading test damping ratio declines by 15.48%after 2 million and 350 thousand times of loading.It finds out that the wheel-set dropping test and circle loading test share a good agreement in damping ratio results.

urban rail transit；steel spring floating slab；logarithmic decay method；hysteresis curve

U213

A

（责任编辑 王建华）

1005-0523（2017）04-0044-06

2016－09－16

宋姣姣（1993—），女，硕士研究生，研究方向为轨道结构动力分析。

练松良（1956—），男，教授，博士生导师，主要研究方向为轨道结构振动。