基于有限断裂力学的FRP-混凝土界面粘结强度研究

童谷生，赖泽坤

（华东交通大学土木建筑学院，江西 南昌 330013）

基于有限断裂力学的FRP-混凝土界面粘结强度研究

童谷生，赖泽坤

（华东交通大学土木建筑学院，江西 南昌 330013）

为了提供一种精准、高效预测外贴式纤维增强聚合物材料（FRP）粘贴于混凝表面强度的数学模型，本文设计了8个单剪试件，利用精密玻璃珠控制胶层厚度，同时采用真空辅助成型技术（VARI）制作FRP板条并外贴于混凝土试块表面。研究混凝土强度和胶层厚度2种变量参数对FRP-混凝土粘结界面强度的影响，依据试验结果分析了界面破坏能和峰值剪切应力与胶层厚度及混凝土强度之间的联系。采用有限断裂力学获取界面裂纹扩展失稳时的脱粘荷载,将理论值与试验结果对比表明FFM模型有良好的精度。

有限断裂力学；FRP-混凝土；粘结强度；胶层厚度；单剪实验；理论解

近年来，得益于FRP复合材料轻质高强耐腐蚀等特点，其在混凝土结构加固技术中的应用越来越广泛。经FRP加固后的混凝土构件在外荷载作用下发生破坏时，一般情况下远达不到FRP的极限强度，破坏形式通常为FRP从混凝土块表面剥离，因此提升FRP的加固效率仍是FRP加固混凝土技术中一个亟待解决的问题。FRP加固混凝土技术的原理是利用建筑结构胶将FRP材料与混凝土结构粘结成一个整体，使两者共同受力，所以各部分材料的改变都可能对界面的粘结强度带来影响。单剪试验已成为测定FRP与混凝土粘结强度的标准试验［1－4］，学术界已提出大量基本单剪试验的粘结强度计算模型公式［5－12］，公式大部分是经验式和半经验试，而且未考虑粘结剂对界面的影响。内聚裂纹模式（CCM）［13－14］用于预测FRP－混凝土界面粘结强度的可靠性一直为学术界广泛认可，虽CCM模型的精确性高，但求解过程复杂，需要对界面的脱粘过程分阶段［15－16］考虑。 Cometti［17］通过设定同样的界面参数获得了 FFM（有限断裂力学）模型下的 FRP-混凝土界面的理论解，与CCM模型的理论曲线预测值非常接近。本文基于FFM推导了关于FRP与混凝土界面脱粘荷载解的二元方程组，设计了8组单剪实验分别考虑混凝土强度、胶层厚度对粘结强度的影响，实验结果很好地证明了FFM模型精准性。

1 单剪实验

目前国内外对FRP-混凝土界面中胶层作用仍未形成统一的观点，在受剪试验中，胶层的抗拉强度远远高于混凝土的抗拉强度，所以部分研究者认为胶层对粘结界面的影响很小。但是也有研究人员发现胶层对界面的影响很大，如Julio等［18］研究了胶层厚度和混凝土强度对FRP-混凝土结构粘结性能的影响，结果表明，当混凝土强度较低时，胶层厚度对界面粘结性能没有显著的影响，但是当混凝土强度超过一定程度时，胶层厚度对界面粘结性能的提升作用增大，而且较厚的胶层并不能持续増加加固构件的极限承载力值；Hadigheh等［19］通过分析大量前人的实验数据，并配合修正后的单剪实验研究了FRP-混凝土界面中胶层厚度的作用，提出“最佳胶层厚度”的概念，实验中这一值为4.77 mm，此外3种胶层厚度2.06，3.32，6.54 mm的试件测得的滑移值分别为0.4，0.43，0.84 mm，表明越厚的胶层有较好的延展性，但是当胶层厚度增加到一定程度时，胶层流动性产生的风险将导致应力集中，极限荷载开始呈下降趋势，所以只有胶层控制在合适的厚度范围内界面强度才能持续增长。

故本文以混凝土强度和胶层厚度为研究对象，采用受力明确而且操作简单可靠的单剪实验，设计如图1中的试件来测定FRP-混凝土界面的粘结强度。FRP用环氧树脂胶粘贴于经糙化处理的混凝土表面，采用一套自行设计的单剪试验装置对FRP板材一端进行拉拔，直到FRP从混凝上完全剥离即测得界面的极限荷载值。

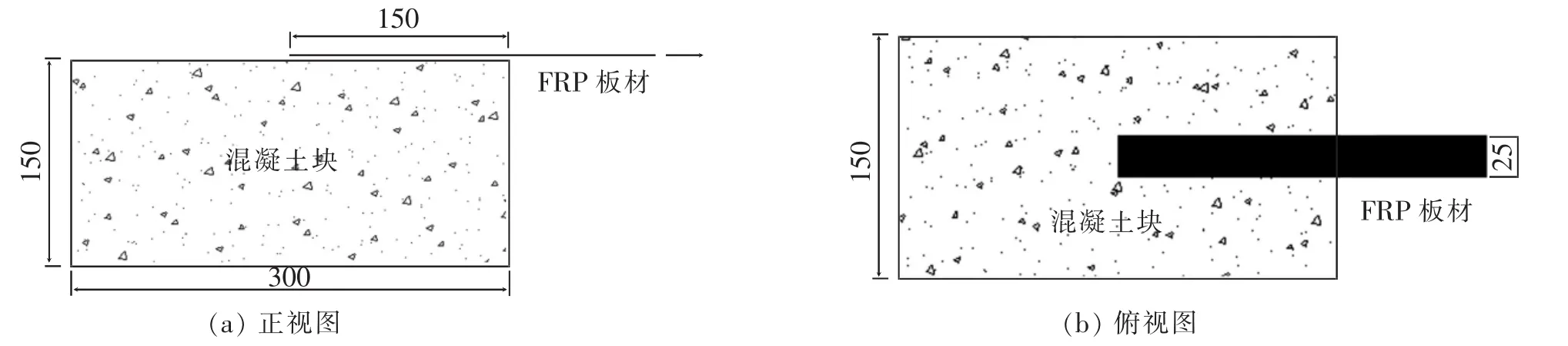
图1 单剪实验试块Fig.1 Single shear test block

实验浇筑了C25和C45强度等级的混凝土试块，放入养护室内养护28天达到标准强度；粘结剂选购了天津市卡本复合材料有公司生产的CBSR-A/B改性环氧树脂胶；为得到外观和性能都符合实验要求的CFRP板条，本文突破性地使用了真空辅助树脂灌注成型（VARI）工艺，如图2，并在制作过程中不断改良工艺，成型后板条力学性能符合规范要求。

实验的参数设置和材料力学性能检测结果如表1和表2。

为获得CFRP板条加载端的粘结滑移曲线，沿板条中心线位置每隔2.5 mm布置一个应变片，再通过对应变差分、累加得到局部粘结应力和相对滑移值，断裂能的大小则为粘结-滑移曲线与坐标轴包含的面积。

图2VARI工艺Fig.2 VARI process

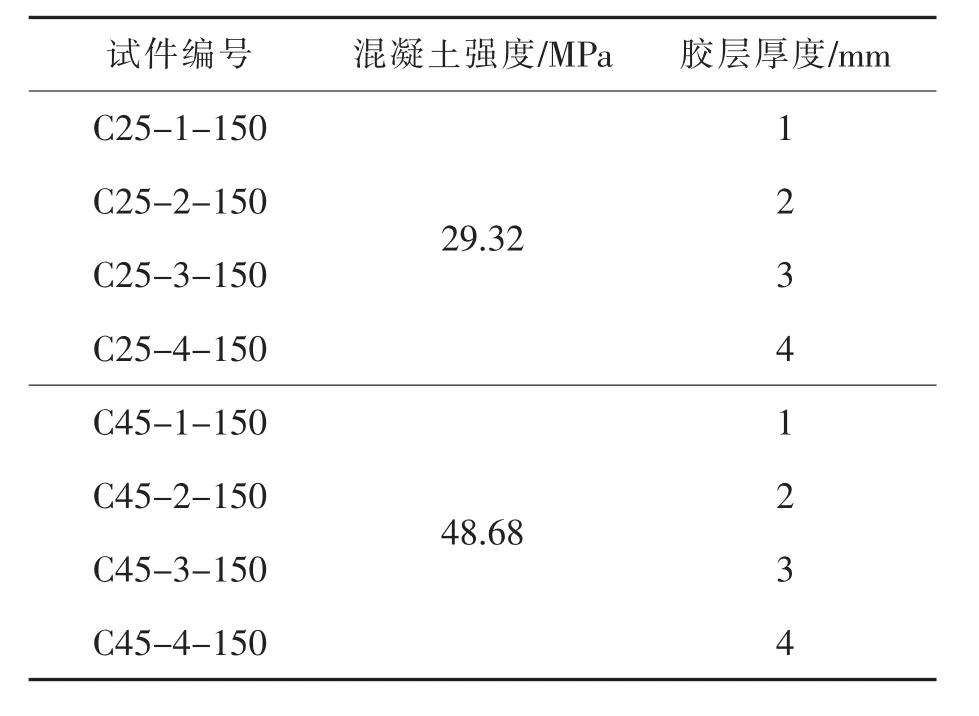
表1 实验参数设计Tab.1 Design of experimental parameters

表2 材料力学性能Tab.2 Mechanical properties of materials

本文为控制胶层厚度尝试了多种实验方法，如在胶层周围布一圈等厚度的铁丝、嵌入金属片等，对比效果后确定采用铺设精密玻璃珠的方法，4种尺寸的玻璃珠对比图如图3，具体的操作流程为：①先在混凝土试块表面经打磨过的部位涂上薄薄的一层胶；②若胶层厚度为1 mm，则取直径1 mm的玻璃珠均匀铺在胶层靠近中部的位置，根据玻璃珠的大小适当选择其数量，宜控制在5～8个；③ 玻璃珠放置到位后用更多的粘接剂把玻璃珠完全覆盖，最后贴上CFRP板并充分压实，刮出板条四周被挤出的多余粘接剂。以下列出了8个试件的极限荷载值、断裂能及峰值剪应力，见表3。

图3 精密玻璃珠对比图Fig.3 Comparison of precision glass beads

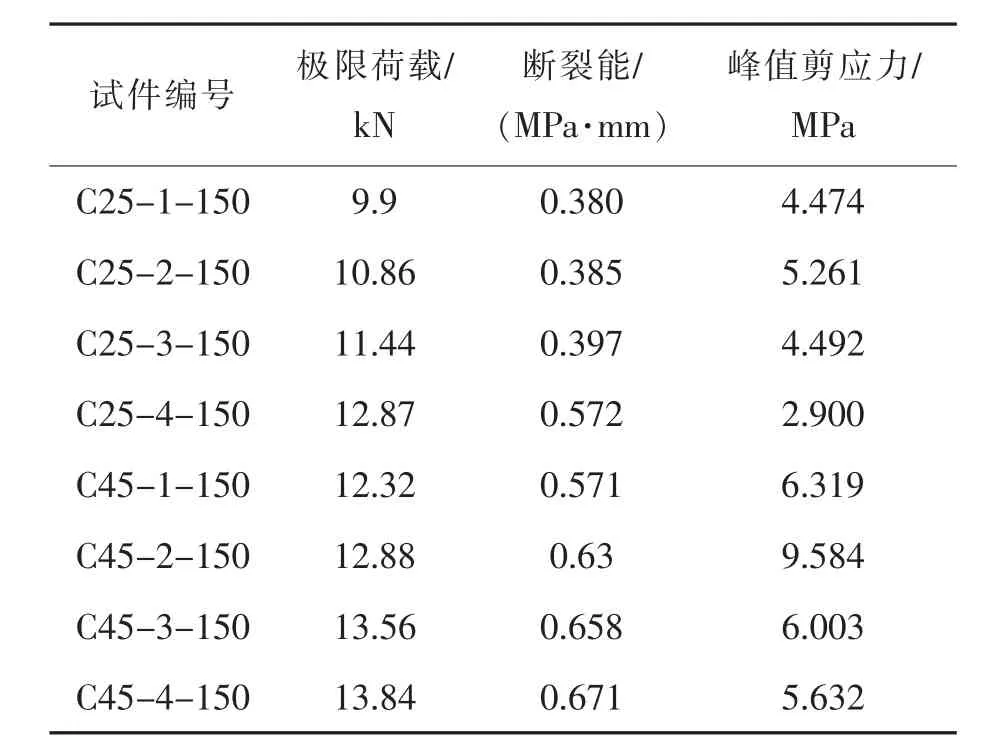
表3 实验结果和粘结-滑移参数Tab.3 Experimental results and calculated values of bond slip parameters

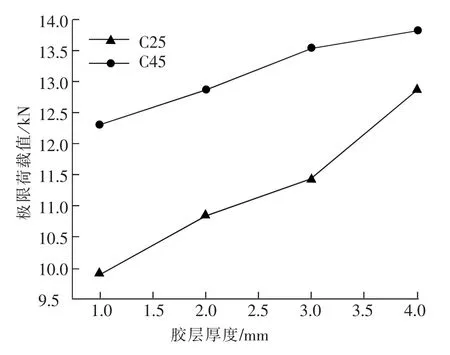
图4 实验极限荷载值Fig.4 Experimental limit load value

由图4可知，FRP-混凝土的界面断裂能和粘结强度随混凝土强度的提高有所增加，但增加的幅度都比较缓慢；随胶层的厚度增加，峰值剪应力呈减小的趋势，但界面断裂仍增大，这是因为越厚的胶层延展性越好，从而使相对滑移值持续增大。

2 FFM模型及其推导

Leguillon[20]研究了断裂力学中脆性材料裂纹传播的能量准则和脆性破坏的应力准则后，认为能量准则和应力准则是裂纹萌生或者扩展的必要条件。在分析脆性或准脆性材料断裂失效时，通常使用两个准则，第一为应力准则，即假定一点处的最大（主）应力达到材料的拉伸强度时材料失效；第二准则为能量准则，即假定裂纹驱动力等于裂纹扩展阻力（产生单位面积裂纹面所需要的能量）时，材料失效。同时，得到裂纹起始扩展是不连续和无限小的，并且这裂纹萌生或者扩展过程中一个突然增加的有限长度，这一长度称为“特征长度”，知道材料的韧性和强度，在能量和应力两个准则同时满足时便可以计算出这一特征长度，这一特征长度依赖于结构而非材料参数。

Cornetti[21]最近又将有限断裂力学方法和弹性界面模型结合，提出了在结构加固与组合结构中需要确定在载荷作用下界面脱粘（分层）失效的分析方法。利用有限裂纹扩展的耦合准则分析了压剪模型，得到了失效载荷的解析解，限于篇幅本文只给出该解析解推导的部分过程。

1）由于FRP-混凝土界面（粘接剂层和混凝土表面的受力层）刚度和厚度趋于零，因此界面可视为低厚度软性的弹性界面，可用弱界面[21]来构建模型。该模型假设FRP与混凝土是由一系列连续且与界面呈法向和正切分布的弹簧连接而成，在实际受力中界面对FRP板和混凝土块的剪切力使得两者有一定的抗剪粘结强度，所以界面能够承受住20～30 kN的拉拔荷载主要是依靠剪力作用，即模型中只考虑正切分布的弹簧作用。随着荷载增大导致初始裂纹萌生和扩展，界面开始出现分层直至CFRP板完全从混凝土块剥离，此过程中Ⅱ型剪切裂纹始终占作用。

2）根据本节开头描述的Ⅱ型裂纹发展需要同时满足应力和断裂能两个条件，即要满足以下两个不等式[22]

式中：σy，ζ（a′）分别为应力、应变能函数；a，Δa，σp，ζΠc，Δ 分别代表初始裂纹长度、裂纹扩展步长、峰值应力、临界应变能释放率（断裂韧性）、裂纹扩展有限长度。在正几何试件接近破坏的阶段，应变能释放率ζΠc单调增长、σy单调下降，若以上两式同时成立则可计算得到极限破坏荷载值。弱界面下的应变能释放率[23]

将应力和断裂能两个公式变形得到：

3）对拉剪试验中构件的尺寸参数分析，表明关于极限荷载的解必须引入无量纲参数μ和ρ：

ρ 定义为 FRP 的机械性能参数；Er，tr，hr，Eb，tb，hb分别为FRP宽度、厚度、杨氏模量和混凝土块的宽度、厚度、杨氏模量。同时引入双线性粘结滑移曲线，如图5所示。Sp，Sf分别代表达到峰值应力τp时对应的界面滑移值、界面脱粘时的滑移值，μ的值也可以用μ=Sf/Sp表示，其物理意义是规定界面的脆、塑性指数。当μ=1时，界面表现为线性理想脆性；当μ→∞时，界面表现为线性理想塑性。

为方便计算引入无量纲参数lch，定义为搭接的特征长度，其物理意义为材料裂纹萌生或者扩展过程中一个突然增加的有限长度：

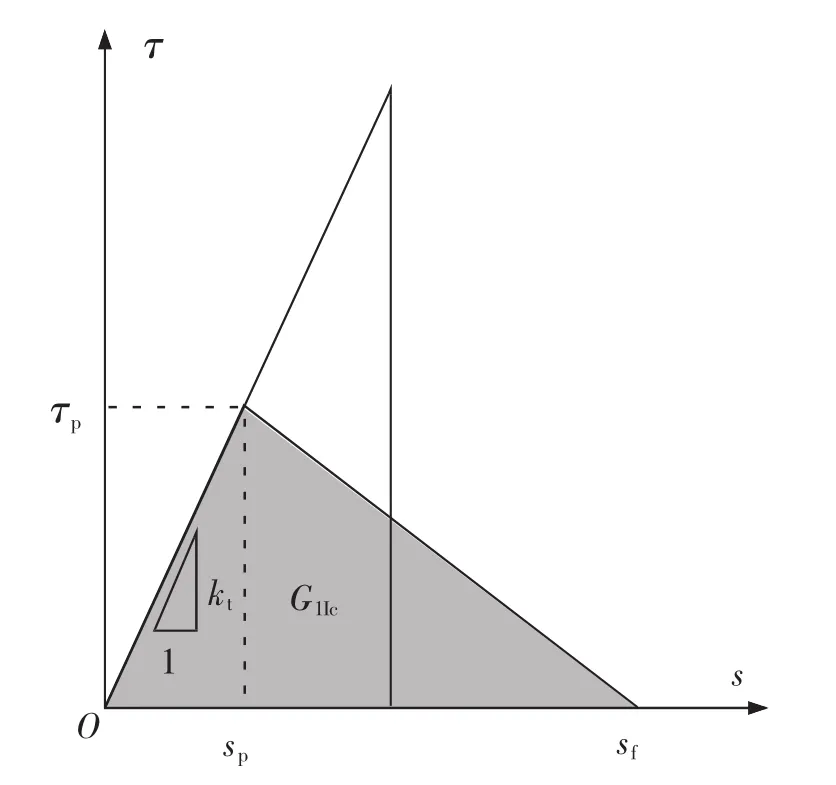
图5 双线性粘结滑移曲线Fig.5 Bilinear bond slip curve

4）利用界面的平衡方程和本构方程并结合边界条件求得剪应力的最终解

由剪应力解的公式可知，界面中应力分布不均匀，加载端为应力的集中部位，剪应力的最大值为

假设界面kt无限大，lch趋于零时，得到强界面[21]的极限荷载值：

将（3）式变形得

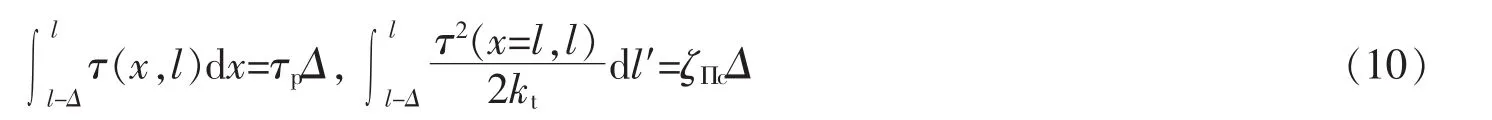
将（6）（7）式代入（10）式，求积分得到

其中未知数有极限荷载值Fc和最终裂纹长度Δ。对式（11）变形得到

其中 δ=Δ/lch，求得 δ，Fc可从式(11)中任意一个式子计算出，δ的求解范围为（0，λ）。 对式（11）中第一个式子变形并除以Fc∞得

由式（13）可知，因Fc∞在同一材料参数下值不变，所以极限荷载Fc和裂纹长度Δ的值取决于λ和μ。λ是关于构件几何形状和界面的弹性无量纲参数，表达式为λ＝l/lch。而μ值的获得可以通过实验数据来绘制粘接滑移曲线，得到固定材料参数下的粘结滑移经验模型。有效粘结长度[21]的计算公式如下：

3 FFM模型分析

3.1 界面粘结强度求解

根据上一节对有限断裂力学模型关于极限荷载值解析解的推导，可以将模型求解中间参数和荷载值的步骤简单概括为

1）把已知量混凝土试块、CFRP板材、胶层的尺寸和性能参数及断裂能、峰值剪应力等代入机械参数和胶层剪切模量公式；

2）上一步骤的结果继续代入脆塑性指数μ、特征长度lch和λ公式，求出各个试件的具体值；

3）将μ和λ代入方程（12），利用MATLAB编程求解得到δ，同时将lch回代δ得到Δ值，最后极限荷载值Fc可从方程组（11）任意一个式子中求解得到。代入第一节单剪实验材料和粘结-滑移参数后，得到的结果如表4所示，对胶层的泊松比v取0.3[24]。

对表4的计算结果分析后可知，随胶层厚度的增加，胶层的剪切刚度kt越低，界面柔性越好，但同时参数μ的值也不断减小，意味着界面的塑性指数在降低，说明胶层厚度的增加容易提高界面发生脆性破坏的风险。

比较表4的论理值与实验值，可以发现用有限断裂力学模型预测的强度值与实测值基本吻合，而且大部分试件的理论值高于实验值，体现了理论值更趋于安全。经计算实验与模型理论值平均百分比误差在5%以内，远高于其他同类模型的精度。

3.2 影响因数作用分析

如上节所述，运用FFM模型求解单剪实验的极限荷载值需将界面断裂能Gf和峰值剪应力τp作为已知量，上述试验研究的结果表明混凝土强度、胶层厚度等因素对FRP-混凝土界面Gf、τp有着显著影响。参考Ueda等[1]的理论模型，他们在考虑了混凝土、胶层、CFRP板材3种材料对极限荷载的影响后提出的断裂能计算公式如下：

由于本文采用了VARI工艺制作CFRP板材，界面内部的作用机理有别于一般的CFRP板材加固系统，因此有必要对其公式进行修正建立符合本文实验结果的界面破坏能与加固材料属性的本构关系。图6～8分别为胶层厚度和混凝土强度与Gf和τp的相关性拟合曲线，其中胶层厚度以参数Gf/τp来反映。

表4 FFM计算结果Tab.4 Calculation results of FFM

Ga/ha与 Gf的拟合关系式为 Gf=0.491（Ga/ha）-0.181。

图6～8明显可看出，胶层厚度的增加和混凝强度的提高而增大，而峰值剪应力随胶层厚度增加呈减小趋势，混凝土强度的提高使峰值剪应上升。拟合得到Gf和τp与Ga/ha、fc之间的非线性关系式如下：

利用拟合的断裂能公式得到FRP-混凝土界面破坏的能量释放率，与Ueda[25]模型的计算值相对比如图 9～10。

图7 Ga/ha与 τp关系Fig.7 Relationship between Ga/haand τp

图6 fc与Gf关系Fig.6 Relationship between fcand Gf

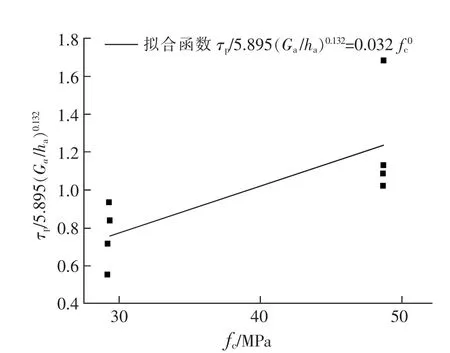
图8 Gf与τp关系Fig.8 Relationship between Gfand τp

由图9～图10可以发现，Ueda模型Gf的预测值比实验值大1倍以上，而拟合后得到Gf的曲线与实验值曲线基本重合，说明Gf和τp与Ga/ha，fc的拟合公式适用于本文进行的FRP-混凝土界面强度分析。

图9 C25试块断裂能对比Fig.9 C25 test block fracture energy contrast

图10 C45试块断裂能对比Fig.10 C45 test block fracture energy contrast

4 结论

将有限断裂力学引入FRP-混凝土界面粘结强度的预测，假定材料的强度和断裂韧性为已知量，经推导得到模型的解析解。实验研究了不同混凝土强度和FRP-混凝土界面粘结剂厚度对粘结强度的影响，分析了界面力学性能发生改变的实质原因，并且将实验结果与模型理论计算值对比，得到结论如下：

1）界面断裂能Gf决定了界面的粘结强度，混凝土强度的提高和粘结剂厚度的增加使Gf有所增大，从而极限荷载值也随之增长。

2）更厚的粘结剂使界面的局部剪应力有所减小，但是FRP与混凝土块的相对位移在持续增大，保证了Gf不减反增。

3）FFM模型计算结果与实验值较吻合，证明FFM可以对界面的粘结强度作出精准预测，此外中间参数μ的值随粘接剂厚度的增加而逐渐减小意味着界面在朝脆性发展，表明一味增加胶层厚度不能使界面性能持续提高。

[1]LJSTEN T B.Defining anchor lengths of steel and CFRP plates bonded to concrete[J].International Journal of Adhesion and Adhesives，1997，17（4）：319-327.

[2]YAO J，TENG J G，CHEN J F.Experimental study on FRP-to-concrete bonded joints[J].Composites Part B：Engineering，2005，36（2）：99-113.

[3]YAO J.Debonding failures in RC beams and slabs strengthened with FRP plates[D].Hong Kong：The Hong Kong Polytechnic University，2005.

[4]任慧韬.纤维增强复合材料加固混凝土结构基本力学性能和长期受力性能研究[D].大连：大连理工大学，2003.

[5]HIROYUKI Y，WU Z.Analysis of debonding fracture properties of CFS strengthened member subject to tension[C]//Proc 3rd International Symposium on Non-Metallic（FRP） Reinforcement for Concrete Structures，1997（1）：284-294.

[6]TANAKA T.Shear resisting mechanism of reinforced concrete beams with CFS as shear reinforcement[M].Hokkaido University，1996.

[7]BROSENS K，VAN GEMERT D.Anchoring stresses between concrete and carbon fiber reinforced laminates[C]//Proc.3rd International Symposium on Non-Metallic(FRP)Reinforcement for Concrete Structures，1997（1）：271-278.

[8]KHALIFA A，GOLD W J，NANNI A，et al.Contribution of externally bonded FRP to shear capacity of RC flexural members[J].Journal of Composites for Construction，ASCE，1998，2（4）：195-203.

[9]CHEN J F，TENG J G.Anchorage strength models for FRP and steel plates bonded to concrete[J].Journal of Structural Engineering，2001，127（7）：784-791.

[10]UEDA T，DAI J G，SATO Y.A nonlinear bond stress-slip relationship for FRP sheet-concrete interface[C]//Proc of International Symposium on Latest Achievement of Technology and Research on Retrofitting Concrete Structures，2003：113.

[11]LU X Z，TENG J G，YE L P，et al.Bond-slip models for FRP sheets/plates bonded to concrete[J].Engineering Structures，2005，27（6）：920-937.

[12]童谷生，郑东润.FRP-混凝土界面粘结强度多变量非线性回归模型[J].科学技术与工程，2016，16（11）：222-227.

[13]CARPINTERI A.Post-peak and post-bifurcation analysis of cohesive crack propagation[J].Engineering Fracture Mechanics，1989，32（2）：265-278.

[14]CARPINTERI A.Cusp catastrophe interpretation of fracture instability[J].Journal of the Mechanics and Physics of Solids，1989，37（5）：567-582.

[15]YUAN H，TENG J G，SERACION R，et al.Full-range behavior of FRP-to-concrete bonded joints[J].Engineering Structures，2004，26（5）：553-565.

[16]COTTONE A，GIAMBANCO G.Minimum bond length and size effects in FRP-substrate bonded joints[J].Engineering Fracture Mechanics，2009，76（13）：1957-1976.

[17]CORNETTI P，MANTI V，CARPINTERI A.Finite fracture mechanics at elastic interfaces[J].International Journal of Solids and Structures，2012，49（7）：1022-1032.

[18]LOPEZ-GONZULEZ J C，FERNANDEZ-GOMEZ J，GONZALEZ-VALLE E.Effect of adhesive thickness and concrete strength on FRP-concrete bonds[J].Journal of Composites for Construction，2012，16（6）：705-711.

[19]HADIGHEH S A，GRAVINA R J，SETUNGE S.Identification of the interfacial fracture mechanism in the FRP laminated substrates using a modified single lap shear test set-up[J].Engineering Fracture Mechanics，2015，134：317-329.

[20]LEGUILLON D.Strength or toughness a criterion for crack onset at a notch[J].European Journal of Mechanics-A/Solids，2002，21（1）：61-72.

[21]CORNETTI P，MANTI V，CARPINTERI A.Finite fracture mechanics at elastic interfaces[J].International Journal of Solids and Structures，2012，49（7）：1022-1032.

[22]CORNETTI P，PUGNO N，CARPINTERI A，et al.Finite fracture mechanics:a coupled stress and energy failure criterion[J].Engineering Fracture Mechanics，2006，73（14）：2021-2033.

[23]LENEI S.Analysis of a crack at a weak interface[J].International Journal of Fracture，2001，108（3）：275-290.

[24]CHEN J F，TENG J G.Anchorage strength models for FRP and steel plates bonded to concrete[J].Journal of Structural Engineering，2001，127（7）：784-791.

[25]UEDA T，DAI J G，SATO Y.A nonlinear bond stress-slip relationship for FRP sheet-concrete interface[C]//Proc of International Symposium on Latest Achievement of Technology and Research on Retrofitting Concrete Structures，2003：113.

Bond Strength Analysis of FRP-concrete Interface Based on Finite Fracture Mechanics

Tong Gusheng，Lai Zekun
（School of Civil Engineering and Architecture，East China Jiaotong University，Nanchang 330013，China）

To explore a precise and efficient mathematical model for predicting the bond strength of externally bonded fiber reinforced polymer（FRP） material to concrete，8 single shear specimens of concrete to FRP were designed in this study by use of precision glass beads to control the adhesive thickness,while adopting vacuum assistant resin infusion process（VARI） to fabricate FRP slab affixed to the concrete surface.Two kinds of impact variable parameters on the interfacial strength of FRP-concrete bond were considered and one was concrete strength and the other was adhesive thickness.According to the experimental results，this paper analyzed the relationship between fracture energy and peak shear stress and the concrete strength and thickness of adhesive layer.The finite fracture mechanics was applied to obtain the debonding load when the interface crack was unstable.The comparison between the theoretical and experimental results showed that the FFM model has good accuracy.

finite fracture mechanics；FRP-concrete；bond strength；adhesive thickness；shear test；theoretical solution

TU375

A

（责任编辑 刘棉玲）

1005-0523（2017）04-0013-09

2017－01－20

国家自然科学基金项目（11242006，11462005）

童谷生（1962—），男，教授，博士，研究方向为结构强度与加固设计理论。