混沌理论和机器学习算法的运动员成绩预测模型

王光明

摘 要： 为了改善运动员成绩的预测效果，更好地为体育训练提供支持，提出基于混沌理论和机器学习算法的运动员成绩预测模型。对运动员成绩数据进行分析，并通过混沌理论找到运动员成绩的变化特点，通过神经网络对混沌理论处理后的运动员成绩训练样本进行建模，并采用粒子群算法在线估计神经网络初始连接权值，最后采用具体运动员成绩数据对模型的可靠性进行分析。分析结果表明，该模型能够从运动员成绩数据中找到其将来变化态势，提高了运动员成绩的预测精度，预测结果具有一定的应用价值。

关键词： 运动员成绩； 混沌理论； 变化态势； 预测模型

中图分类号： TN911.1?34 文献标识码： A 文章编号： 1004?373X（2017）17?0120?04

Athletes′ performance prediction model based on chaos theory

and machine learning algorithm

WANG Guangming

（College of Physical Education， Jiujiang University， Jiujiang 332005， China）

Abstract： In order to improve the performance prediction effect of athletes and provide better support for sports training， an athletes′ performance prediction model based on chaos theory and machine learning algorithm is proposed. The performance data of athletes is analyzed， and its change characteristic is found out with chaos theory. The athletes′ performance training sample processed with chaos theory was modeled with neural network. The particle swarm algorithm is used to estimate the initial connection weights of neural network. The specific performance data of athletes is adopted to analyze the reliability of the model. The analysis results show that the model can find out the future change trend of the athletes′ performance data， improve the performance prediction accuracy of athletes， and its prediction result has a certain application value.

Keywords： athletes′ performance； chaos theory； change trend； prediction model

0 引 言

隨着经济的发展，人们的身体素质不断增强，运动员的竞技技术是衡量一个国家体育事业发展水平的一个重要标准，因此，运动员的竞技水平一直以来受到了各国的高度重视[1]。运动员成绩可以有效地描述运动员的竞技水平，而运动员成绩的预测有助于教练、运动员以及体育管理部门了解运动员成绩的动态变化特点。根据具体运动员自身特点制定科学、合理的训练计划，可以进一步提高运动员的竞技水平，同时保证运动员取得更优的成绩[2?3]。

针对运动员成绩预测问题，学者们对其变化规律进行分析，建立了许多运动员成绩的预测模型[4]。运动员成绩预测模型的研究可以划分为两个阶段：线性建模阶段和非线性建模阶段[5]。线性建模阶段引入多元线性回归方法、灰色系统、因子分析法等对运动员成绩进行建模，这些方法假设运动员成绩是一种线性变化趋势，成绩变化波动很小，这对一些类型的运动员来说，可以描述其变化趋势[6]，然而大多数运动员由于心理、年龄、训练方法、训练设备等综合的作用，其不单具有线性变化趋势，有时会出现比较强烈的非线性变化趋势，因此线性建模方法就不能有效描述运动员成绩的变化特点，导致预测结果与实际值之间的误差很大，预测结果极不可靠，实际应用价值大大下降[7]。为了解决线性建模方法的局限性，随着非线性理论的发展，有学者提出线性建模方法，如：支持向量机、神经网络等[8?10]，它们可以从线性角度对运动员成绩变化特点进行刻画，相对于支持向量机，神经网络的学习速度明显加快，通用性更强，因此成为当前运动员成绩建模的主要工具[11]。BP神经网络是一种典型的三层神经网络，通过三层结构网络可以对运动员数据之间的内在联系进行描述，获得精度较高的运动员成绩预测结果[12]。BP神经网络的连接权值初始化问题一直困扰着BP神经网络的应用范围，当前主要采用经验法确定BP神经网络连接权值的初始值，值一旦确定不合理，BP神经网络的学习性能就会急剧下降，从而对运动员的预测结果产生负面影响，导致预测精度变低[13]。

为了改善运动员成绩预测的效果，提出基于混沌理论和机器学习算法的运动员成绩预测模型。首先对运动员成绩数据进行分析，并通过混沌理论找到其变化特点，然后通过神经网络对混沌理论处理后的运动员成绩训练样本进行建模，并采用粒子群优化算法[14]在线估计神经网络连接权值。实验结果表明，该模型能够从运动员成绩数据中找到其将来变化态势，提高了运动员成绩的预测精度。endprint

1 相关理论

1.1 运动员成绩的混沌分析以及处理

1.1.1 混沌理论

运动员成绩与运动员的体质、教练训练水平、训练技术、训练设备、政府政策以及国家的经济水平均有着一定的关系，使得运动员成绩变化复杂，而一定时间段内运动员成绩与当前以及其他数据点存在一定的联系，因此可以通过引入混沌理论对运动员成绩的数据点变化关系进行挖掘，找到其中隐藏的变化特点。设一段时间内收集到的一个运动员成绩为其中表示采集的数据点数，通过混沌理论可以对数据进行处理，得到如下数据变化形式：

（1）

式中：和表示该运动员数据之间的延迟时间和嵌入维数，其中嵌入维数用于描述多个数据点当前数据之间存在的联系。

采用C?C算法和CAO算法分别确定运动员成绩的和值，用于描述运动员成绩数据隐藏的变化特点。

1.1.2 C?C算法的工作步骤

（1） 设一个运动员成绩两个数据的样本点为：，通过式（2）计算两个数据点之间的距离：

（2）

（2） 引入一临界半径在该临界范围内，用关联积分描述所有数据点对数所占的比例，具体为：

（3）

式中：表示数据的规模；表示Heaviside函数，计算公式为：

（4）

（3） 通过上述方式，一个运动员的成绩被划分为个子序列，并可以得到：

（5）

设最大子序列和最小子序列之间的差计算公式为：

（6）

设运动员成绩的为那么可以得到：

（7）

当达到最小值时，那么就可以将该时刻的值作为最合理的运动员成绩值。

1.1.3 Cao算法的工作步骤

（1） 对于一个运动员数据序列，第个重构的向量为，最近向量为，那么可以得到：

（8）

（2） 当式（9）取得最小值或者变化十分缓慢时，此时的作为最合理的运动员成绩值：

（9）

1.2 机器学习算法

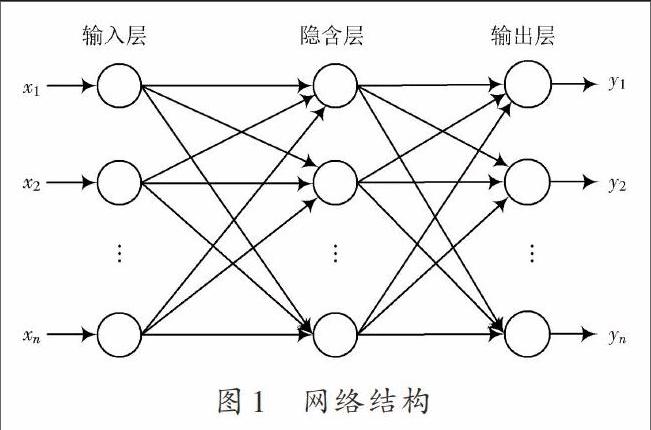
BP神经网络是一种经典的机器学习算法，学习过程首先进行信号正向传播阶段，即信号从输入层传向隐含层，隐含层传向输出层，并估计输出层的误差，如果误差不能满足期望误差要求，那么误差信号从输出层反馈传向隐含层，再从隐含层反馈传向输入层，即进入误差反向传播阶段，不断重复信号正向传播阶段和误差反向传播阶段，直到误差满足预先设定的要求为止，其结构见图1。

设表示输入；表示隐含层的输出；表示输出层的输出；为期望输出；表示输入层与隐含层的连接权值；表示隐含层与输出层的连接权值，那么对于第个节点，其输出值的计算公式为：

（10）

式中：表示输出层的神经元节点数。

隐含层的第个节点输出的计算公式为：

（11）

式中：表示隐含层的神经元节点数。

期望值和输出值间的误差为：

（12）

预测误差从输出层反馈到隐含层，那么有：

（13）

预测误差从隐含层反馈向输入层，那么有：

（14）

对连接权值和不断更新，直到误差满足实际应用要求，即有：

（15）

式中為学习速度。

在运动员成绩建模过程中，BP神经网络初始连接权值的确定十分重要，而经验法确定其值具有一定的盲目性，为此，采用粒子群优化算法确定最合理的连接权值。

2 混沌理论和机器学习算法的运动员成绩预测

模型

（1） 对一名具体运动员在一段时间的成绩进行收集，并去除一些无效或者错误的数据点。

（2） 采用C?C和Cao算法确定该运动员的最佳值和值，根据和的值对运动员成绩数据进行处理。

（3） 根据运动员成绩数据确定神经网络的结构，并设置神经网络的初始权值。

（4） 采用粒子群优化算法优化神经网络的初始权值，并且通过下式更新粒子的位置：

（16）

（17）

式中：为速度因子；和表示当前和下一时刻的粒子速度；和表示当前和下一时刻的粒子位置；表示惯性权重；为随机数函数。

（5） 通过粒子群优化算法得到神经网络最优的初始权值后，建立运动员成绩的预测模型。

（6） 采用另一个运动员的成绩对建立的运动员成绩预测模型性能进行分析，如果预测结果可靠，那么表示该模型可用，否则，对运动员成绩的预测模型进行重新构建，直到达到预期效果为止。

混沌理论和机器学习算法的运动员成绩预测模型的工作流程见图2。

3 运动员成绩预测的实证分析

3.1 运动员历史成绩

为了分析混沌理论和机器学习算法的运动员成绩预测结果，采用一个铅球运动员的成绩进行仿真实验，其数据如图3所示。

3.2 运动员成绩的混沌分析

根据C?C和Cao算法对图3中的运动员成绩进行处理，找到其最优的和值，结果如图4所示。对图4进行分析，可以发现达到最小值时，当时，值的变化很缓慢。根据对运动员成绩进行处理，得到神经网络的学习样本。

3.3 运动员成绩预测效果分析

运动员成绩的预测结果如图5所示。运动员成绩预测误差小，可以描述运动员成绩的变化特点，提高了运动员成绩的预测精度。

4 结 论

运动员成绩是评价运动员竞技状态的一项关键指标，运动员成绩不仅与运动员自身素质相关，同时与训练手段、方法以及外界因素相关，导致运动员成绩变化十分复杂，成绩的波动范围有时比较大。为了准确描述运动员成绩的变化特点，提出混沌理论和机器学习算法的运动员成绩预测模型。首先对一个运动员一段时间内的成绩进行收集，设不同时间的运动员成绩间存在内在联系，通过混沌理论对运动员一段时间的成绩进行分析，找到运动员成绩的变化趋势，然后采用机器学习算法中预测性能优异的BP神经网络对运动员成绩变化特点进行逼近，构建运动员成绩的预测模型，同时采用粒子群优化算法解决神经网络的连接权值和阈值确定的难题，使神经网络的学习和泛化能力更优，最后通过运动员成绩的具体预测实验结果验证了该模型的有效性，预测结果可靠，该模型可以应用于实际的运动员训练计划中。endprint

在运动员成绩实际建模与预测过程中，影响因素是多方面的，本文只考虑外界因素的综合作用，从整体上对运动员的成绩变化特点进行反映。为了更好地描述运动员成绩变化态势，需要引入更多的因素对运动员成绩变化特点进行描述，并提供更多的信息，这是将来进行研究的方向。

参考文献

[1] 赵波.十项全能世界顶尖男子运动员成绩分析及预测研究[J].体育文化导刊，2013，3（3）：76?79.

[2] 许晶.我国顶尖男子十项全能运动员竞技特征及实力分析[J].广州体育学院学报，2008，12（3）：36?64.

[3] 周伟.对中外优秀女子三级跳远运动员三跳技术的灰色关联分析[J].吉林体育学院学报，2004，20（3）：64?65.

[4] 赵丙军.运用多元回归方法建立我国男子跳远项目训练模型的研究[J].西安体育学院学报，2011，18（1）：81?82.

[5] 魏春玲.我国十项全能运动成绩的因子分析及灰色系统回归预测研究[J].体育科学，2004，24（11）：51?53.

[6] 刘昊.非线性筛选因子和加权的体育成绩建模与预测[J].计算机应用与软件，2014，31（11）：105?108.

[7] 龙斌.基于支持向量机的刘翔110 m栏成绩预测[J].天津体育学院学报，2009，24（4）：330?333.

[8] 王宗平，孙光.应用BP神经网络算法对运动成绩预测的实证研究[J].南京体育学院学报，2006，20（4）：109?111.

[9] 孙群，刘国璧，程伟，等.基于模糊神经网络的刘翔110 m栏成绩预测[J].重庆科技学院学报（自然科学版），2011，10（2）：104?107.

[10] 庄冲，王宗平.灰色系统模型与BP神经网络模型在体育成绩预测方面的比较研究[J].南京体育学院学报，2006，20（6）：134?135.

[11] 李征宇，闫生.神经网络模型在运动成绩预测中的应用[J].哈尔滨体育学院学报，2009，27（2）：110?113.

[12] 齐晓慧，李杰，韩帅涛.基于BP神经网络的自适应自抗扰控制及仿真[J].控制与决策，2013，34（6）：776?782.

[13] 席剑辉，韩敏.主成分分析与神经网络的结合在多变量序列预测中的应用[J].控制理论与应用，2007，24（5）：719?724.

[14] 彭令，牛瑞卿，赵艳南，等.基于核主成分分析和粒子群优化支持向量机的滑坡位移预测[J].武汉大学学报（信息科学版），2013，38（2）：148?152.endprint