基于机器学习的大学体育成绩预测与分析

王晶

摘 要： 为了科学评价大学生身体素质，提出基于机器学习算法的体育成绩预测模型。对当前大学生体育成绩预测的研究现状进行分析，指出导致当前模型预测精度低的原因，采用机器学习算法——支持向量机建立大学生体育成绩预测模型，并采用粒子群算法选择模型参数，最后将该模型应用于某大学的体育成绩建模和预测中。应用实例结果表明，机器学习算法可以克服传统模型的不足，使得大学体育成绩预测效果得到改善，预测结果可以指导大学体育学科的改革。

关键词： 体育训练； 机器学习算法； 预测模型； 粒子群算法

中图分类号： TN911.1?34； TP391 文献标识码： A 文章编号： 1004?373X（2017）17?0116?04

Machine learning based prediction and analysis of college sports performance

WANG Jing

（Sias International University， Zhengzhou University， Xinzheng 451150， China）

Abstract： In order to evaluate the physical quality of college students scientifically， a sports performance prediction model based on machine learning algorithm is put forward. The research status of the current college students sports performance prediction is analyzed to point out the reason causing the low prediction accuracy of current model. The machine learning algorithm （support vector machine） is used to establish the sports performance prediction model of college students. The particle swarm optimization algorithm is adopted to choose the parameters of the model. The model is applied to the physical performance modeling and prediction of a certain college. The application results show that the machine learning algorithm can eliminate the shortcomings of the traditional model， improve the prediction effect of the college sports performance， and its prediction results can guide the reformation of the college physical education.

Keywords： physical training； machine learning algorithm； prediction model； particle swarm optimization algorithm

0 引 言

隨着人们生活水平的不断提高，大学生物质生活更加丰富，他们缺少锻炼，部分大学生身体素质有不同程度的下降[1?2]。大学生体育课是提高大学生身体素质的一个重要途径，而大学生体育成绩预测可以帮助大学体育管理部门合理开设相关的课程，制定最科学的训练机制，因此如何建立精度高的体育成绩预测模型引起了广大高校的高度重视[3]。

最原始的大学体育成绩预测方法主要是通过体育老师实现，它们采用统计学方法对大学生体育成绩进行计算和估计，但是由于大学生体育成绩受多方面因素的影响，体育老师不可能全面考虑到，即使全面考虑到了各种因素，计算过程也相当复杂，体育成绩预测效率低，无法满足现代大学生体育训练的要求[3?4]。随着信息技术、自动化技术以及人工智能理论研究的不断深入，许多高校体育老师和体育方面的研究专家提出了大量的大学体育成绩自动预测模型[5]。大学体育成绩预测实质是一种回归问题，因此当前模型可以划分为两种：线性回归模型和非线性回归模型[6]。应用最广泛的线性模型为多元线性回归模型，根据大学生体育历史成绩对模型的相关参数进行估计，建立大学生体育预测模型，然后对某个大学生的体育成绩进行预测，当影响因素比较少时，预测精度高[7]。大学体育成绩建模是一个十分复杂的过程，影响因素有大学生自身因素，还包括外界因素，因此大学体育成绩没有什么变化规律可循，随机性大，而线性模型不能描述大学体育成绩的随机性[8]。非线性模型采用随机性理论对大学生体育成绩进行建模，建立的模型预测精度更高，当前主要为机器学习算法中的神经网络[9?10]。神经网络是基于经验风险最大化原则的机器学习算法，非线性拟合能力相当强，可以无限拟合大学生体育成绩的变化特点，取得了不错的应用效果。但其基于经验风险最大化原则，因此需要大量的大学体育成绩样本才能获得理想的大学生体育预测结果，而一个学生的体育成绩历史样本相当少，难以满足该条件[11?12]。

支持向量机是一种新型的机器学习算法，采用结构风险最小化原则，没有神经网络的大样本要求，在小样本条件下仍然可以获得良好的拟合能力[13]。为了提高大学生体育成绩的预测效果，提出基于支持向量机的大学体育成绩预测模型，并采用粒子群算法选择模型参数，最后将该模型应用于某大学的体育成绩建模和预测中，结果表明，支持向量机解决了其他传统模型的不足，改善了大学体育成绩的预测效果。endprint

1 机器学习算法的大学体育成绩预测模型

1.1 机器学习算法?支持向量机

相对于神经网络以及其他传统机器学习算法，支持向量机的限制条件更少，且不存在“过拟合”缺陷，十分适合于小样本、非线性大学生体育成绩的建模与预测[11]。

设大学生体育成绩样本集为支持向量机的回归方式具体为：

（1）

式中和均为支持向量机的参数。

要建立大学生体育成绩预测模型，必须找到最合理的和的值，为此，根据结构风险最小化原则，将其转化成如下形式：

（2）

式中：为回归误差；为误差的惩罚参数。

为了简化求解过程，降低建模的计算复杂度，引入松弛因子和得到二次规划形式为：

（3）

采用拉格朗日乘子和进一步对式（3）进行变换，得到：

（4）

式中表示核函数。

支持向量机的回归函数可以描述为：

（5）

选择RBF函数作为核函数，其定义为：

（6）

式中表示RBF的参数。

1.2 粒子群算法

粒子群算法的当前最优解为pbest，当前群体的最优解为gbest，构建描述粒子个体优劣程度的适应度函数为：

（7）

和为粒子第次迭代的速度和位置，它们的更新方式为：

（8）

（9）

式中：为学习因子；Rand（）为随机数；为惯性权重。

为了解决支持向量机参数的确定问题，采用粒子群优化算法对支持向量机的训练过程进行在线优化，确定最优参数和根据最优参数和提高大学生体育成绩的预测精度。

1.3 机器学习算法的大学体育成绩预测模型

（1） 对于某一个体育项目的历史数据进行收集，并进行如下处理：

（10）

式中和表示大学生体育成绩的最小和最大值。

（2） 根据经验确定支持向量机的参数和范围。

（3） 初始化粒子群，每一个粒子的位置向量包括一组参数和。

（4） 根据每一组参数和对大学生体育成绩训练样本采用支持向量机进行学习，并计算每一个粒子的适应度函数值。

（5） 根据适应度函数值对全部粒子进行排序，并对当前最优解pbest和当前群体最优解gbest进行替换操作。

（6） 更新粒子群的速度和位置。

（7） 粒子群算法的迭代次数增加。

（8） 如果迭代次数超过预先设定的最大值，那么就终止算法执行，否则返回步骤（4）继续执行优化操作。

（9） 根据群体最优解gbest得到支持向量机的最优参数和值。

（10） 根据和对大学生体育成绩重新训练，建立基于支持向量机的大学生体育成绩预测模型。

（11） 采用大學生体育成绩测试样本对大学生体育成绩预测模型的性能进行测试和分析。

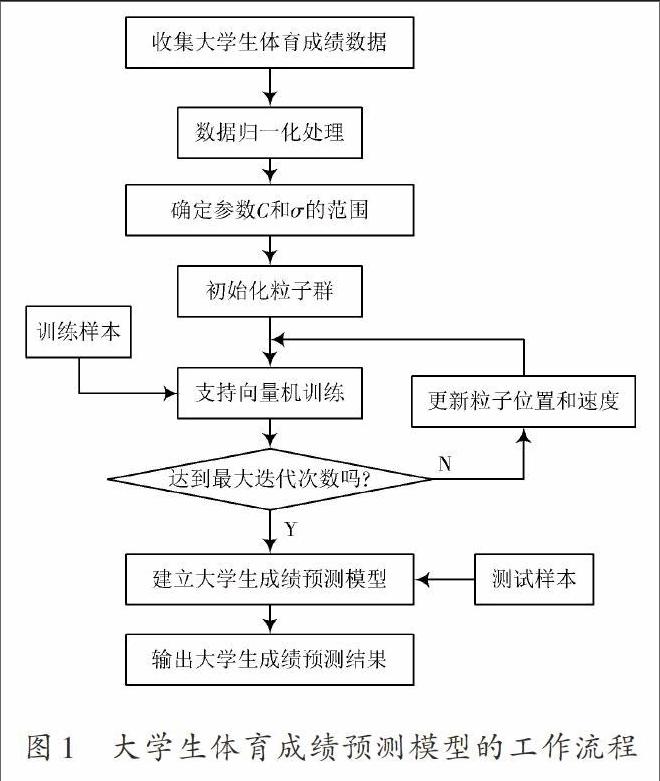
综上可知，基于机器学习算法的大学生体育成绩预测模型工作流程如图1所示。

2 大学生体育成绩预测模型的应用实例

2.1 大学生体育成绩数据

为了全面分析基于机器学习算法的大学生体育成绩预测模型的有效性和优越性，选择郑州大学的大学生体育成绩作为实验对象，首先选择100 m跑的成绩进行测试，共500个成绩如图2所示，其中300个100 m用于建立大学生体育成绩预测模型，其他用于检测模型的泛化性能。

2.2 模型的有效性测试

200个100 m跑的成绩组成的测试样本预测结果如图3所示，对图3的预测结果进行详细分析可以发现，基于机器学习算法的大学生体育成绩预测模型可以描述500个100 m跑的成绩变化趋势，获得了理想的100 m跑的成绩预测结果，实验结果验证了该模型的有效性。

2.3 模型的优越性测试

为了测试机器学习算法的大学生体育成绩预测模型的优越性，选择文献[3]的线性回归模型、文献[8]的神经网络进行对比实验，统计它们的男生100 m跑成绩的预测精度，精度如表1所示，对表1的结果进行对比和分析，可以得到如下结论：

（1） 在全部大学生体育成绩的预测模型中，线性回归模型的预测精度最低，这是因为线性回归模型只能对男生100 m跑成绩的部分变化特点进行描述，无法描述全面的变化特点，大学生体育成绩预测效果差。

（2） 相对于线性回归模型，神经网络的大学生成绩预测精度得到了一定的提高，这是因为神经网络是一种机器学习算法，可以对男生100 m跑成绩的线性和非线性变化特点进行拟合，取得更优的预测效果，但由于要求样本数量多，导致部分点的预测偏差大，预测误差随之增大，模型的大学生成绩预测效果整体欠佳。

（3） 相对于线性回归模型以及神经网络，支持向量机的大学生体育成绩预测精度最高，这是因为支持向量机要求的训练样本少，克服了线性回归模型的缺陷，解决了神经网络的局限性，提高了男生100 m跑成绩预测的精度，具有十分明显的优越性。

2.4 通用性分析

为了测试机器学习算法的大学生体育成绩预测模型的通用性，采用郑州大学的男生三级跳远、男生3 000 m跑、男生引体向上、女生1 000 m跑、女生立定跳远成绩作为研究对象，统计它们的预测精度，结果如表2所示。从表2的预测精度可以发现，全部大学生体育成绩的预测精度均超过90%，远远大于实际应用范围的85%，这表明该模型的通用性强，可以应用于实际的大学体育成绩预测中。

3 结 语

体育训练是提高大学生身体素质的一个重要因素，而体育成绩预测可以帮助大学制定有效的体育训练方案。为了提高大学生体育成绩的预测效果，解决当前大学生体育成绩预测模型的缺陷，构建了基于机器学习算法的大学体育成绩预测模型，采用机器学习算法中性能最优的支持向量机对大学生体育成绩数据进行建模和拟合，具体应用实例结果表明，该模型的通用性能强，可以应用于各种大学生体育成绩预测，而且预测结果可靠，可以为大学体育训练提供有价值的信息。

参考文献

[1] 许晶.我国顶尖男子十项全能运动员竞技特征及实力分析[J].广州体育学院学报，2008，28（5）：61?64.

[2] 赵波.十项全能世界顶尖男子运动员成绩分析及预测研究[J].体育文化导刊，2013（3）：76?79.

[3] 赵丙军.运用多元回归方法建立我国男子跳远项目训练模型的研究[J].西安体育学院学报，2001，18（1）：81?82.

[4] 周伟.对中外优秀女子三级跳远运动员三跳技术的灰色关联分析[J].吉林体育学院学报，2004，20（3）：64?65.

[5] 邓美兰.奥运会男子十项全能前三名成绩的灰色预测模型的研究[J].数学的实践与认识，2009（18）：44?49.

[6] 魏春玲.我国十项全能运动成绩的因子分析及灰色系统回归预测研究[J].体育科学，2004，24（11）：66?69.

[7] 孙群，刘国璧，程伟，等.基于模糊神经网络的刘翔110 m栏成绩预测[J].重庆科技学院学报（自然科学版），2011，10（2）：104?107.

[8] 王宗平，孙光.应用BP神经网络算法对运动成绩预测的实证研究[J].南京体育学院学报，2006，20（4）：109?111.

[9] 李征宇，闫生.神经网络模型在运动成绩预测中的应用[J].哈尔滨体育学院学报，2009，27（2）：110?113.

[10] 戴敏.基于数据挖掘的运动员体能测试数据分析[J].计算机工程与应用，2003（9）：38?40.

[11] 刘昊.非线性筛选因子和加权的体育成绩建模与预测[J].计算机应用与软件，2014，31（11）：105?108.

[12] 夏轩，许伟明.改进的粒子群算法对RBF神经网络的优化[J].计算机工程与应用，2012，48（5）：37?40.

[13] 龙斌.基于支持向量机的刘翔110 m栏成绩预测[J].天津体育学院学报，2009，24（4）：330?333.endprint