互相关分析中有偏估计与无偏估计的比较
2017-09-08舒张平徐科军
舒张平, 徐科军
(合肥工业大学 电气与自动化工程学院, 安徽 合肥 230009)
互相关分析中有偏估计与无偏估计的比较
舒张平, 徐科军
(合肥工业大学 电气与自动化工程学院, 安徽 合肥 230009)
本文通过理论分析和Matlab仿真得出。周期信号需采用有偏估计,且要求延迟时间小于信号周期;非周期信号中,对于局部峰值点和周期变化较小的一类准周期信号,有偏估计要求延迟时间小于信号近似周期,无偏估计对延迟时间的大小没有要求,但抗干扰能力较差。对于冲击信号,有偏估计和无偏估计均能满足要求,且对延迟时间的大小没有限制。
互相关;延迟时间;有偏估计;无偏估计
0 引言
互相关分析可以计算两信号之间的延迟时间T[1-3]。 但是,在实际应用中,我们发现互相关分析的两种估计方式具有不同的特点,导致其在延迟时间T的计算上具有不同的适用范围。而这些知识在一般教材上并没有介绍,教材中仅仅介绍了互相关分析的原理,对两种估计方式的特点以及如何根据信号特征来选择互相关分析的估计方式没有阐述。
为此,本文针对互相关分析的两种估计方式在实际应用中的关键问题进行研究,并给出解决方案。
1 有偏估计和无偏估计的特点
互相关分析的估计方式有两种:有偏估计和无偏估计。
设进行互相关分析的两信号序列分别为xa(n)和xb(n),则其有偏估计和无偏估计的计算公式分别为式(1)和式(2)。
m=-(N-1),-(N-2),…,0,…,N-2,N-1
(1)
m=-(N-1),-(N-2),…,0,…,N-2,N-1
(2)
式(1)和式(2)表明,随着|m|的增加,互相关分析中的相乘相加的数据量逐渐减少。但是,在有偏估计中,分母N保持不变;而在无偏估计中,分母N-|m|也在同步的减小。因此,互相关分析的有偏估计和无偏估计存在明显的差异,即互相关分析的有偏估计中,随着|m|的增加,理论上互相关分析结果的幅值会衰减,且|m|越大,衰减越大。而互相关分析的无偏估计中,并不会对互相关分析结果的幅值进行衰减。互相关分析的有偏估计和无偏估计的这一特点,使得其应用在延迟时间T的计算中具有不同的适用范围。
2 有偏估计和无偏估计的适用范围
2.1 周期信号
当进行互相关分析的信号为周期信号时,互相关分析的有偏估计中,随着|m|的增加,理论上互相关分析结果的幅值会衰减,且|m|越大,衰减越大。此外,周期信号的互相关分析结果,理论上为同周期的周期信号。因此,周期信号的互相关分析采用有偏估计的结果中,存在多个相距Tm(Tm为信号周期)的局部峰值点,且局部峰值点的幅值逐渐衰减。这样,第一个局部峰值点即为互相关分析结果的峰值点(由于延迟时间T为正数,因此,本文只考虑互相关分析结果的正半轴部分)。因此,想要通过找到互相关分析结果的峰值点所对应的时间,来计算两个周期信号之间的延迟时间T,就必须保证T小于Tm,以保证T所对应的局部峰值点为第一个局部峰值点,即互相关分析结果的峰值点;而互相关分析的无偏估计理论上并不会使互相关分析结果的幅值产生衰减。因此,周期信号的互相关分析结果仍为同周期的周期信号,其各局部峰值点的幅值相等,没有单个的峰值点,从而无法通过找互相关分析结果峰值点的方法来计算延迟时间T。例如,采用标准的正弦波周期信号,利用Matlab软件,对比分析采用有偏估计和无偏估计的互相关分析结果如图1所示。其中,信号周期Tm等于0.1 s,延迟时间T等于0.016667 s,其小于信号周期Tm。
图1(a)表明对周期信号进行有偏估计的互相关分析结果中,各相邻局部峰值点间相距为Tm,且第一个局部峰值点即为互相关分析结果的峰值点。因此,只有当T 图1(b)表明对周期信号进行无偏估计的互相关分析结果中,各局部峰值点的幅值相等。因此,无法通过找互相关分析结果峰值点的方法来计算延迟时间T。 图1 有偏和无偏估计用于周期信号 2.2 非周期信号 1)准周期信号 实际应用中传感器输出信号大多为局部峰值点和周期变化较小的一类准周期信号,如图2(a)所示。这一类准周期信号与周期信号非常相似,只是局部峰值点和周期存在较小的变化。因此,与采用有偏估计计算周期信号的互相关的结果一样,采用有偏估计计算这一类准周期信号的互相关的结果中,存在多个局部峰值点,且理论上会使局部峰值点的幅值产生衰减,|m|越大,衰减越大。因此,为了能够通过找互相关分析结果峰值点的方法来计算延迟时间T,需保证延迟时间T小于信号的近似周期Tm,以保证第一个局部峰值点所对应的时间即为延迟时间T。 对于互相关分析的无偏估计,由于这一类准周期信号的周期不完全相等,各局部峰值点也不完全相同。因此,与周期信号不同,其互相关分析结果中各局部峰值点的幅值不完全相等。因此,无论延迟时间T是否小于信号的近似周期Tm,只要当|m|的取值所对应的时间等于延迟时间T时,互相关分析结果的幅值最大。从而可以通过找互相关分析结果峰值点的方法来计算延迟时间T。但是,该方法要求两信号是完全相似的,即两信号间除了存在一定的相位差外,只有幅值上的比例衰减。这是因为无偏估计不对互相关分析结果的幅值进行衰减,导致互相关分析结果中虽然峰值点所对应的时间为延迟时间T,但各局部峰值点的幅值基本相同。当由于干扰的存在,导致其中一路信号受到干扰时,就有可能造成互相关分析结果中某个局部峰值点的幅值变大,超过延迟时间T所对应的峰值点的幅值。此时,通过找互相关分析结果峰值点的方法来计算延迟时间T,就会造成较大的计算误差。例如,采用两组完全相似的涡街流量信号,如图2(a)所示,互相关分析采用无偏估计的结果如图2(b)所示。其中,T的理论值为0.2 s。然后,对其中一路信号的一部分数据做指数型衰减,来模拟受到干扰的情况,如图2(c)所示,此时采用无偏估计的互相关分析结果如图2(d)所示。 图2(a)和(b)表明,对于局部峰值点和周期变化较小的一类准周期信号,当两信号完全相似时,采用无偏估计的互相关分析结果中,各局部峰值点的幅值基本相同,但峰值点所对应的时间为延迟时间T,从而可以通过找互相关分析结果峰值点的方法来计算T,且对T与Tm的大小关系没有要求。 图2(c)和(d)表明,当进行互相关分析的某一路信号受到很小干扰,导致两信号间的相似性被破坏时,就有可能造成某个局部峰值点的幅值变大,被误认为是峰值点。而实际应用中,很难保证两传感器的输出信号完全相似。因此,该方法的抗干扰能力较差。 图2 无偏估计用于准周期信号 2)冲击信号 当进行互相关分析的信号为冲击信号时,由于冲击信号在大部分时间内幅值为零(或白噪声),其有用信号仅占其中小部分时间。从而只有当|m|的 取值所对应的时间等于两信号间的延迟时间T时,非零点的相乘相加量最多,互相关分析结果取最大值。因此,无论互相关分析采用有偏估计还是无偏估计,均可以通过找互相关分析结果峰值点的方法来计算延迟时间T,且对延迟时间T的大小没有要求。利用Matlab软件仿真,采用互相关分析的有偏估计和无偏估计来计算两冲击信号间的延迟时间T,结果如图3所示。其中,采样频率Fs等于3 KHz,两冲击信号间延迟1000点,即理论延迟时间为0.33333 s。 图3(a)和(b)的对比分析表明,当进行互相关分析的两信号为冲击信号时,虽然采用有偏估计和无偏估计的互相关分析结果中,峰值点的幅值大小不等,但是,峰值点所对应的时间均为延迟时间T。因此,对于冲击信号,互相关分析采用有偏估计和无偏估计均能通过找互相关分析结果峰值点的方法来计算延迟时间T,且对延迟时间T的大小没有要求。 图3 有偏和无偏估计用于冲击信号 通过以上对互相关分析的有偏估计和无偏估计所进行的研究,可以得出以下结论: (1)对于周期信号间延迟时间T的计算,互相关分析需采用有偏估计,且要求两信号间的延迟时间T小于信号周期Tm; (2)非周期信号中,对于局部峰值点和周期变化较小的一类准周期信号间延迟时间T的计算,互相关分析采用有偏估计要求两信号间的延迟时间T小于信号的近似周期Tm,此时其抗干扰能力较好。互相关分析采用无偏估计对延迟时间T与信号近似周期Tm的大小关系没有要求,但抗干扰能力较差;对于冲击信号间延迟时间T的计算,互相关分析采用有偏估计和无偏估计均可以通过找互相关分析结果峰值点的方法来计算延迟时间T,且对延迟时间T的大小没有要求。 (舒张平等文) (3)在实际应用中,当传感器输出信号为周期信号或局部峰值点和周期变化较小的一类准周期信号时,可以通过合理设计两传感器间的距离,保证进行互相关分析的两信号间的延迟时间T小于信号周期Tm。然后,互相关分析采用有偏估计,并通过找互相关分析结果峰值点的方法来计算延迟时间T;当传感器输出信号为冲击信号或类似冲击信号的非周期信号时,互相关分析采用有偏估计和无偏估计均能满足要求。 [1] 徐科军.信号处理技术[M].武汉:武汉理工大学出版社,2001 [2] 徐科军 主编.信号分析与处理[M].北京:清华大学出版社,2006 [3] 张玉超,徐科军,叶旭.互相关运算中的两个关键问题研究[J],电气电子教学学报,2011,33(1):27-34 The Comparison of Biased Estimate and Unbiased Estimate on Cross-Correlation Analysis SHU Zhang-ping, XU Ke-jun (HefeiUniversityofTechnology,Hefei230009,China) This paper studies by theoretical analysis and Matlab simulation. Periodic signals requires use of biased estimate, and the delay time is less than the signal period; In non-periodic signal, for the quasi-periodic signal of local peak point and the cycle change small, biased estimate requires the delay time is less than the approximate signal cycle, and unbiased estimated does not requires the length of the delay time ,but its anti-interference ability is poor. For the impact signal, biased estimate and unbiased estimate can meet the requirements, and there is no limit on the length of the delay time. cross-correlation; delay time; biased estimate; unbiased estimation 2016-07-11; 2019-09- 02 安徽省教学名师奖(2013jxms009),安徽省精品资源共享课“传感器与检测技术”(2014gxk003) 舒张平(1991-),男,硕士研究生,研究方向为检测技术与自动化装置,E-mail:hfutdsp@mail.hfut.edu.cn 徐科军(1956-),男,博士,教授,主要从事传感器、自动化仪表和数字信号处理的教学和科研工作,E-mail:dsplab@ hfut.edu.cn G420 A 1008-0686(2017)03-0032-04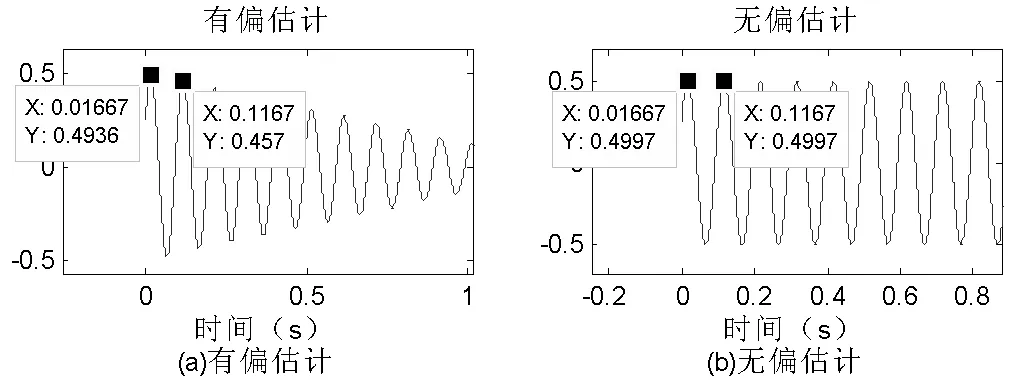



3 结语
