电路分析及其思维推演的特征

余琼蓉

(湖北大学 计算机与信息工程学院, 湖北 武汉 430062)

电路分析及其思维推演的特征

余琼蓉

(湖北大学 计算机与信息工程学院, 湖北 武汉 430062)

本文以单个二极管电路进行频谱变换分析为例，指出了电路分析的目的、方法和详细步骤，给出其思维推演过程。电路分析过程中思维的推演是在物理领域、数学领域和工程领域等多种思维领域中频繁切换且各领域中的思维又高度融合，形成了一种综合思维过程，掌握综合思维方法可以使复杂的电路分析变得简单有序，从而使电子线路课程中教与学的难度大幅度降低。

电路分析;等效电路;思维推演

0 引言

电气类工科中用到的思维方式方法按思维对象所在的知识领域可以分为三大类，分别是数学思维、物理思维和工程思维。数学思维是描述量、形状之间的客观规律，物理思维是遵循事物发展客观规律的思维方法，而付之于实际应用的“做”的思维方式统称为工程思维。

通常情况下，学生的工程思维能力相对于数学思维能力和物理思维能力要弱得多，当学习的知识中要求工程思能力较强又与数理思维高度融合时，由于“短板效应”就会让“教”和“学”的难度大大增加。

“高频电子线路”课程中非线性电路的分析是课程的主要难点。本文以单个二极管电路频谱分析来说明电路分析中思维方式的融合及其思维推演特征。

1 二极管平衡电路频谱分析

电子技术中的电路分析是电路设计、电路调试过程中的一个重要步骤，正确而又熟练地掌握电子线路的分析方法，合理地使用各种思维技术，是提高我们电子技术水平的一个有效途径。

问题：电路原理圆如图1(a)所示，是一个最简单的二极管电路。给出信号源是u1(t)=U1mejω1t,u2(t)=U2mejω2t,U2m≫U1m，求网孔电流id的频谱[1]。

此题分析有很多种方法，不同的方法等效电路的形式是不同的。这里采用开关函数分析法，开关函数分析法是非线性电路的一种常见的分析方法。其等效电路图示于图1(b)。

(a)电路原理图 (b)等效电路图1 单个二级管电路

1.1 画等效电路

画等效电路的过程如图2所示，一共分为四步：建模、变换、构造和论证，下面分步说明。

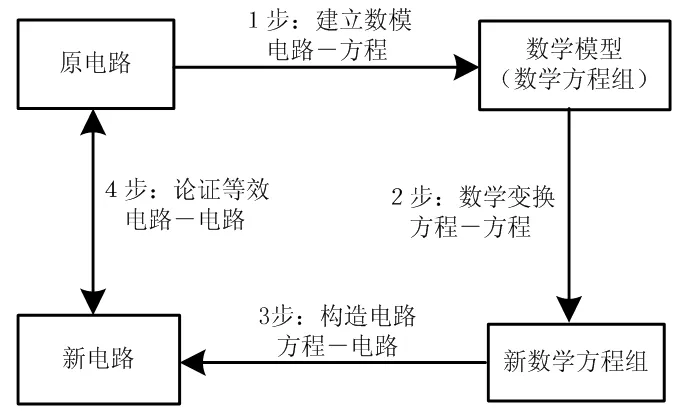
图2 等效电路画法

1)为电路建立数学模型

首先对图1(a)的原理电路建立数学模型得下式

(1)

2)数学变换

数学变换的目的是将数学模型简单化。数学变换表面上看是纯数学思维，实际上它仍是一种综合思维，融合了工程思维、数学思维和物理思维。

数学变换的步骤如下：

(1)确定变换表达式——式(1)中的id表达式是指数函数形式，是一个超越函数。数学变换过程就是式(1)电流方程的简化过程。

(2)确定变换方式——数学变换的方式有两种，一种等同变换，只变形式不改变函数值；另一种是近似变换，形式与量同时变换，等同变换是纯数学思维，近似变换是在工程思维和物理思维引导下的数学思维。近似变化是在工程允许的误差范围之内，误差的大小不是唯一的，根据实际应用的场合不同，允许的误差也会不同，变换出来的方程形式也会不同。

(3)确定变换域——式(1)中二极管约束方程曲线是图3所示的二极管伏安特性曲线即图上粗的黑色曲线，图3中区间[UdL, UdH]是其定义域，同时是式(1)电压方程的值域，式(1)电流方程的值域是[0,idmax]，这一区间函数是非线性的。

图3 二极管伏安特性曲线

(4)构造变换函数——构造一个新的函数，让新函数在式(1)电流方程定义域区间段内拟合原函数曲线使得函数形式变得简单，要求误差尽量变小且不允许使元件的功能发生质的变化，否则这种构造就是不成功的。这里，构造出一个新函数式，在图3中就是细实折线，误差是粗实线和细实线之间的距离(数学思维)。在工程上，这两个函数都能对信号的频谱进行变换，不会影响二极管元件在电路中的功能的实现，所以是可行的(这里是工程思维)。将构造出的折线段写成数学表达式的方式如下式。

(2)

(5)论证构造函数——构造函数论证是指在物理学范围内，论证对新旧两个函数所表示的物理实在(电子元件)在电路中的功能的效果是否相同(物理思维)。

根据二极管的单向导电性，当加在二极管两端的电压足够大时，二极管加正向电压导通，导通时电压与电流关系表现为一个纯电阻；反向电压时截止电路断开，功能上表现为一个断开的开关。新函数式(2)的id表达式所反映的正是电阻和受控开关(控制者是ud)的串联连接电路。它和二极管实体在实际应用时效果相同的，所以可以将式(2)看成是式(1)的数学变换表达式，到此完成了数学变换这一步。

综合起来，数学变换不是单纯的数学思维，而是数学思维、物理思维与工程思维的融合，并且经常性地在三个思维领域内来回切换，从而使电路分析变得复杂起来。

3)画等效电路

等效电路是与原电路具有相同功能的电路。

首先按电路连接基本原则构成电路如图1(a)所示，其次按式(2)可以构造成如图1(b)所示的其等效电路。这一步的思维最特殊也最具创新性，它体现出典型的工程思维的特征，并具有明显的创新性思维；

式(2)中受控开关的约束方程设为函数K(ω2t)，称为单向开关函数，则

(3)

式(2)可以写成为式(4)：

(4)

至此完成了本文的核心，即：由图1(a)电路画出等效电路图1(b)。

1.2 对等效电路建模与求解

由图1(b)电路构造数学模型就很简单，我们直接就可写出式(5)来，电流的频谱只需对式(5)进行傅立叶变换即可得到[2]。

id=gdK(ω2t)[u1mejω1t+u2mejω2t]

(5)

2 电路分析中的思维推演特征

2.1 表达式在数学、物理、工程三个领域中量的关系

在数学思维、物理思维和工程思维这三个领域中，式(2)的取值范围和这三个领域的关系如图4所示。

图4 式(2)取值范围关系图

在进行数学变换时，思维重点一定要从始到终都站在工程范畴内考虑问题，数学思维只是提供量的关系，物理思维提供实际元件及特性，以数学形式来表示，工程思维才是我们的目的，也是我们思考虑问题的出发点，它包含有数学、物理和实际工程应用三大特点[3]。

2.2 数学表达式在三个领域中的含义

数学表达式在教学，物理和工程三个领域中所表示的意义示之于表1。在表1中纵向比较，每一个表达式及与之对应的电子元件和电路有着密不可分的联系，以物理元件为对象，方程是元件伏安特性(电气特性)的数学表征，电路是元件的实际应用；横向比较，两组物理的电子元件，各自有不同的数学模型；不同的电路形式，却可以有着相同的功能。三者之间，物理元件是承接数学模型与电子电路(实际应用)的桥梁，它们的关系不再是完全包含关系，而转化为一种与物理元件相交的交集。

2.3 思维推演特征

综上所述，可以归纳出电路分析过程中的有如下思维推演特征：

(1)数字思维、物理思维、工程思维三种思维并存。

(2)三种思维高度融合均衡分布形成综合思维。

(3)知识点简单，分析电路思维过程复杂。

3 结语

本文以单个二极管电路为例，详细地分析了电路分析过程中所用到的思维技术、思维方法和所涉及的思维领域[3]。

(余琼蓉文)

表1 数学方程、约束方程和等效电路在三个领域之间的含义

数学领域表达式id=Iseudq/kTid=gdK(ω2t)ud函数特性指数函数分段线性函数定义域ud[⁃∞，+∞][⁃∞，+∞]值域id[0，+∞][⁃∞，+∞]物理领域物理实在一个二极管(参数)，一个信号源(激励信号)，一个响应信号电阻(参数)、开关(参数)、一个信号源、一个信号元件特性PN结，半导体电阻损耗能量，开关控制电流通断参数饱和电流、反向截止电压、最大管耗，门槛电压电阻，额定功率，额定电流取值范围ud视元件型号而定视元件型号而定id视元件型号而定视元件型号而定工程领域电路结构功能产生新频谱产生新频谱取值范围ud和id视元件型号和实际的信号源而定视元件型号和实际的信号源而定

这三种电路分析的思维具有三种思维频繁切换、高度融合和均衡分布的特性；在知识深度一定的条件下，思维能力应该同时满足数学思维、物理思维和工程思维的相应能力，且这三种思维能力处于均衡的分布状态。思维能力分布越不均均衡，学习理解难度就越大，当同时从三个领域来思考问题时，复杂的难度大的电路分析即可转化成三种逻辑简单、知识浅显的问题。

[1] 张肃文.高频电子线路 [M], 北京：高等教育出版社 2002第3版

[2] 曾兴雯主编. 高频电子线路 [M]，北京：高等教育出版社 2004年1月第一版

[3] 袁绪兴 思维技术 [M]，西安：西安交通大学出版社 2011年6月第一版

Circuit Analysis and Its Characteristics in Deduction of Thinking

YU Qiong-rong

(SchoolofComputerScienceandInformationEngineeringofHubeiUniversity,Wuhan430062,Chian)

This article introduces a single diode circuits spectrum transform analysis, and points out the purpose of the analysis, methods and steps in detail, and gives its deductive process of thinking in detail. Deduction of thinking in a variety of thinking in the field of frequent transformation and highly fused to form comprehensive thinking. Mastering the comprehensive thinking method can make the complex circuit analysis into simple knowledge points one by one, So the difficulty of the electronic circuit course teaching and learning are greatly reduced.

circuit analysis; equivalent circuit; deduction of thinking

2014-07-02;

2017-03- 29

余琼蓉(1965-)，女，硕士，副教授，主要从事电子信息专业基础和专业课的教学以及控制工程的科研开发， E-amil：tk_yqr@126.com

TN702

A

1008-0686(2017)03-0029-04