级联长周期光纤光栅的模式耦合与干涉机理*

陈海云， 陈 成

(1.浙江师范大学 信息光学研究所，浙江 金华，321004;2.浙江省光信息检测与显示技术研究重点实验室，浙江 金华，321004;3.浙江师范大学 数理与信息工程学院，浙江 金华，321004)

级联长周期光纤光栅的模式耦合与干涉机理*

陈海云1,2， 陈 成3

(1.浙江师范大学 信息光学研究所，浙江 金华，321004;2.浙江省光信息检测与显示技术研究重点实验室，浙江 金华，321004;3.浙江师范大学 数理与信息工程学院，浙江 金华，321004)

针对级联长周期光纤光栅(CLPFG)的光传输特性存在模式耦合和模式干涉2种不同角度的解释，基于耦合模理论和传输矩阵法，系统研究了CLPFG中的模式耦合与干涉机制，厘清参与马赫-泽德干涉的纤芯模成分，得到模式干涉的相干表达式，从而将模式耦合和干涉机制从理论本质上统一起来；同时深入分析了光栅长度L对干涉条纹结构特性的影响.结果表明：L=LO(最佳长度)时，中心波长处条纹对比度达到最大值；LLO时，中心波长处的对比度下降，但在中心波长两侧的2个对称波长处可达到最大的条纹对比度.该研究结果可为基于CLPFG的通信和传感器件应用提供理论指导.

光纤光学；级联长周期光纤光栅；马赫-泽德干涉；传输矩阵

0 引 言

长周期光纤光栅(LPFG)能够将纤芯模式耦合到同向传输的包层模，从而在透射谱中留下分立的多个损耗峰，具有良好的带阻光谱特性，同时，包层模式易受环境影响而导致损耗峰的移动，因此，LPFG已被广泛应用于光纤通信和传感领域中[1-2].级联长周期光纤光栅(CLPFG)由2个相同结构的LPFG间隔一定长度的光纤构成，形成马赫-泽德干涉(MZI)结构[3]，CLPFG具有更精细的条纹谱线，在通信领域可用于波分复用系统中的多通道隔离滤波[3].而用于传感时除了LPFG本身对被测参量的响应外，充当干涉臂的间隔光纤段能引入附加相位差，因此，具有比单个LPFG更高的灵敏度，已成为应用广泛的高灵敏度光纤传感器件[4-5].此外，CLPFG中干涉条纹的频率与间隔光纤长度近似成正比，可用以组成频分复用的多参量传感器[6]，已被用于折射率、湿度、pH值等多参量光化学传感系统[7].

在CLPFG的传感应用中，条纹谱的特性对传感器的响应特性起着决定性作用，条纹的频率、相位和对比度等直接影响输出条纹信号的分析和解调，尤其是在基于频分复用的多参量传感系统中，传感单元CLPFG中模式的耦合和干涉情况与输出复合条纹信号傅里叶频谱有直接关系[6-7]，通过合理调整CLPFG的结构参数可使频域滤波和相位解调更合理有效.因此，通过分析CLPFG的模式耦合,深入考察模式干涉机制和干涉条纹特性对CLPFG传感器结构的分析和设计无疑具有十分重要的意义.

本文基于耦合模理论，利用传输矩阵法分析光经过CLPFG结构时的模式耦合特性，并与马赫-泽德干涉条纹表达式比较，通过理论分析和数值计算,系统阐释模式干涉机制与光栅模式耦合之间的本质联系，并进而阐明通过改变CLPFG结构参数来调谐条纹特性的方法.研究结果有望为CLPFG传感器的设计和实现提供理论基础和技术指导.

1 理论分析

图1 CLPFG结构示意图

CLPFG结构如图1所示，2个相同结构(周期Λ,长度L，纤芯折射率平均调制量σ)的LPFG在同一光纤中形成级联结构，两光栅之间的间隔光纤长度为S.

1.1 模式干涉

如图1所示，纤芯中传输的纤芯基模经过LPFG1时，部分被耦合到包层中形成包层模，并沿光纤包层传播，当经过LPFG2时,包层模式的部分能量被重新耦合回纤芯中而再次成为纤芯模.由于包层模与纤芯模的有效折射率不同，由包层模被LPFG2重新耦合回纤芯而形成的纤芯模与由纤芯传输而来经LPFG2后的剩余纤芯模之间存在相位差，两者在纤芯中相遇而发生模式干涉，在输出谱中形成周期性的干涉条纹.这种干涉机制属于马赫-泽德干涉，间隔光纤的纤芯和包层分别充当干涉仪的两臂.

光纤光栅MZI的干涉可以表示为[8]

(1)

式(1)中:Ico和Icl分别表示纤芯模与包层模的光强;φ为纤芯模与包层模之间的相位差.为方便后续对条纹干涉信号的傅里叶分析，干涉条纹可以表示成更一般的形式[9]，即

(2)

与式(1)相比可得

(3)

图2 CLPFG的典型干涉条纹及a(λ)和b(λ)曲线

在LPFG构成的光纤光栅MZI中，经过光栅耦合的纤芯模和包层模光强是波长的函数，因此，CLPFG的干涉条纹除相位差引起的周期性调制之外，条纹的幅度亦随波长而变化，即存在一个包络.CLPFG的典型干涉条纹如图2所示.图2中，虚线为CLPFG中单个LPFG的透射谱.由图2可见，单个LPFG的透过率曲线对整个条纹图谱起到了包络的作用.图2同时给出了相应的a(λ)和b(λ)曲线，在中心波长λ0=1 550 nm处有：Ico=Icl，a(λ)=b(λ)，因而,中心波长处的条纹对比度达到最大值.

1.2 模式耦合

光经CLPFG的透射谱具有干涉条纹特征，是模式干涉的直接体现，同时，光经过光纤光栅的传播，实质是模式耦合与传输.根据耦合模理论，光经过1个均匀LPFG的传输可以用矩阵表示为[10]

(4)

(5)

式(5)中,ncoeff和ncl,meff分别为纤芯模和包层模的有效折射率，可由相应模式的特征方程求解得到[11].光经过间隔光纤的传输同样可以用矩阵来表示[10]，即

(6)

式(6)中，Δneff=ncoeff-ncl,meff.光经过整个CLPFG后的纤芯模和包层模振幅可由如下矩阵运算得到[10]：

(7)

则最后透过率为

(8)

图2所示的干涉条纹即为由式(8)计算得到的CLPFG透射率.计算中采用的光纤结构参数为：纤芯折射率n1=1.468 1,包层折射率n2=1.462 8,环境折射率n3=1；光栅参数为：Λ=378 μm,L=5.6 mm,σ=4×10-4；间隔光纤长度S=30 mm.

2 分析讨论

下文由传输矩阵出发，分析参与干涉的2个模式光强度及相位差，考察2个模式光强度之比对干涉条纹的影响，并进而系统探讨光栅结构参数与条纹特性之间的关系.为分析方便，将式(4)和式(6)分别简化表示为

(9)

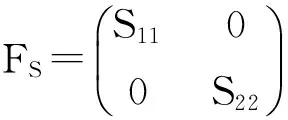
(10)

则光经过LPFG1后,

(11)

纤芯模和包层模的光强分别为Ico1=|Aco1|2和Icl1=|Acl1|2.光经过间隔光纤传输后,

(12)

由式(6)可知，在无损耗传输前提下，纤芯模和包层模经过间隔光纤的传输只改变相位，光强度Ico1和Icl1的值保持不变.光经过LPFG2后,

(13)

因此，CLPFG结构最后输出的纤芯模振幅为

(14)

相应光强为|Aco|2，即透过率T，也就是光谱仪最后能够记录的条纹谱线.

显然，式(14)是个复数表达式，是一种相干叠加的数学表达形式，真正体现了马赫-泽德干涉的本质特性.方程中所包含的2项则分别代表了参与干涉的2部分光：

(15)

由传输矩阵运算过程可知，第1项Aco_1来自于AcoS，是进入LPFG2的纤芯模经LPFG2耦合形成的纤芯模；而第2项Aco_2则来自于AclS，是进入LPFG2的包层模被重新耦合回纤芯而得到的纤芯模，这2部分光通过不同路径传输并最终在纤芯中相遇而发生干涉.因此，严格来讲，式(1)～式(3)中的Ico,Icl实际是指Ico=|Aco_1|2,Icl=|Aco_2|2，而不是式(11)中的|Aco1|2,|Acl1|2，因为间隔光纤中传播而来的纤芯模和包层模经过LPFG2的耦合，都将分别激发纤芯模和包层模，而真正参与干涉的是二者经LPFG2后各自形成的2个纤芯模.这2个模式之间的相位差为

(16)

式(16)给出的相位差包含了由间隔光纤引入的相位差

(17)

同时也包含了模式经过2个光栅传输而引入的相移φG，且φ=φS+φG.

相位差直接决定了干涉条纹的频率，相位差越大，条纹越密.图3给出了干涉条纹谱线与上述2个不同相位差对应余弦信号的对比，由图3可见，cosφ函数曲线与干涉条纹曲线峰值完全一致，真正反映了式(1)所示干涉表达式中的相位信息.而条纹与cos(φS)函数曲线之间存在明显的相移.显然，在上述选定的CLPFG结构参数条件下，由光栅本身引入的相位差不能被忽视.但必须指出的是，在给定2个光栅的结构参数前提下，由光栅本身引入的相位差是恒定的，但由式(17)可知，由间隔光纤引入的相位差与间隔光纤长度S成正比，因此,当S≫L时，φ≈φS，此时,条纹频率与S近似成正比，这与文献[12]的结论相一致.

(a) cosφ

(b) cos(φS)

图3 干涉条纹与相位余弦函数的对比

由式(1)阐述的马赫-泽德干涉原理可知，Ico和Icl的比值直接决定条纹的对比度.由于间隔光纤段的传输只影响相位而不影响强度，因此，Ico和Icl的比值直接决定于光栅的结构参数.为讨论方便，定义比值R=Ico/Icl,R1=Ico1/Icl1,R2=a(λ)/b(λ)，则由光栅耦合效率关系可得到如下关系：

(18)

(19)

由式(18)和式(19)可知，条纹对比度的调节可以通过改变R1实现，而Ico1和Icl1的比值则完全取决于LPFG1中纤芯模到包层模的耦合效率[10]：

(20)

根据归一化条件有:T=1-T×，R1=T/T×.

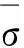
(a)L=3.9 mm

(b)L=7.8 mm

图4 不同光栅长度时的条纹及a(λ)和b(λ)曲线

L=5.6 mm，此时的光栅长度可称之为最佳长度LO.不同光栅长度时的条纹及a(λ)和b(λ)曲线如图4所示.当L=3.9 mm时，由于LLO时,情况有所不同，如图4(b)所示，L=7.8 mm时,中心波长耦合效率超过50%，单个LPFG中心波长处的透过率为0.2，R1=0.25，R=0.062 5，R2=2.055 7.中心波长处的条纹对比度有明显降低，但由于中心波长耦合效率超过50%，在两侧存在耦合效率为50%即a(λ)=b(λ))的波长点使条纹对比度达到最大值，图中的2个波长值分别为1 527.0 nm和1 574.5 nm.条纹对比度越大，对应条纹的斜率越大，被测量的变化引起相同的条纹移动对应的透过率变化也越大，强度解调时的灵敏度就越高.因此，在中心波长确定的情况下，针对不同光栅长度,可以在不同波长处实现高灵敏度响应.

3 结 论

系统研究了长周期光纤光栅MZI中的模式耦合和干涉机制，从LPFG的传输矩阵出发，厘清了真正参与马赫-泽德干涉的2个纤芯模式成分，将有关CLPFG的模式耦合表述及模式干涉表述从理论本质上统一起来，为对CLPFG-MZI特性的理解提供了详细的理论分析和解释.并深入分析了光栅结构参数对模式干涉条纹结构特性的影响，讨论了不同光栅长度时的条纹对比度特性，当LLO时，中心波长处的对比度下降，但在中心波长两侧的2个对称波长处可达到最大的条纹对比度.研究结果可以为基于CLPFG的通信和传感器件应用提供理论支持.

[1]董新永,李岚,沈平,等.一种通道数可变的光纤光栅梳状滤波器[J].光子学报,2010,39(2):238-242.

[2]顾铮先,张江涛.基于双峰谐振效应的镀金属长周期光纤光栅液体浓度传感器[J].光学学报,2011,31(3):0305003.

[3]Gu X J.Wavelength-division multiplexing isolation fiber filter and light source using cascaded long-period fiber gratings[J].Opt Lett,1998,23(5):509-510.

[4]Lee B H,Nishii J J.Bending sensitivity of in-series long-period fiber gratings[J].Opt Lett,1998,23(20):1624-1626.

[5]Gu Z T,Jiang X L,Chen H Y.High-sensitivity sensor design based on cascaded long-period fiber grating with film coating[J].Opt Engineering,2013,53(2):021104.

[6]Murphy R P,James S W,Tatam R P.Multiplexing of fiber-optic long-period grating-based interferometric sensors[J].J Lightwave Technol,2007,25(13):825-829.

[7]Huang Q P,Chen H Y.Multi-parameter optochemical sensing based on coated cascaded long-period fiber gratings and frequency division multiplexing[J].Optik,2017,132:348-355.

[8]Lee B H,Kim Y J,Chung Y.Fiber modal index measurement based on fiber gratings[J].Fiber Integr Opt,2001,20(5):443-455.

[9]Takeda M,Ina H,Kobayashi S.Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry[J].J Opt Soc Am,1982,72(1):156-159.

[10]Turan E.Fiber grating spectra[J].J Lightwave Technol,1997,15(8):1468-1488.

[11]Tsao C Y H,Payne D N,Gambling W A.Modal characteristics of three-layered optical fiber waveguides:a modified approach[J].J Opt Soc Am A,1989,6(4):555-563.

[12] Lee B H,Nishii J J.Dependence of fringe spacing on the grating separation in a long-period fiber grating pair[J].Appl Opt,1999,36(16):3450-3459.

(责任编辑 杜利民)

Mode coupling and interference mechanism in cascaded long-period fiber gratings

CHEN Haiyun1,2, CHEN Cheng3

(1.InstituteofInformationOptics,ZhejiangNormalUniversity,Jinhua321004,China; 2.KeyLaboratoryofOpticalInformationDetectionandDisplayTechniqueinZhejiangProvince,Jinhua321004,China; 3.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

According to two different explanations from the view of mode coupling and mode interference for the transmission properties in cascaded long-period fiber gratings (CLPFG), based on the coupled-mode theory and transfer-matrix method, the mode coupling and interference mechanism were systematically investigated. The modal components involved in the Mach-Zehnder interference were identified and the coherent expression of the mode interference was obtained, which unified the mode coupling and interference mechanism. Furthermore, the influence of grating length on the fringe properties was analyzed. For the optimum lengthLO, the fringe contrast at central wavelength reached maximum. ForLLO, however, the contrast at central wavelength decreased, but it reached maximum at two certain wavelengths on the each side of central wavelength. The results were prospected to provide theoretical guidance for the applications of CLPFG-based communication and sensing devices.

fiber optics; cascaded long-period fiber grating (CLPFG); Mach-Zehnder interference; transfer matrix

10.16218/j.issn.1001-5051.2017.03.005

�2016-12-10；

2017-01-10

浙江省教育厅科研项目(Y201534206);浙江师范大学博士启动基金资助项目(ZC304014028);浙江省光信息检测与显示技术研究重点实验室开放基金资助项目(ZL2014002)

陈海云(1977-)，男，浙江新昌人，讲师,博士.研究方向：光纤光栅传感理论与技术；光电检测等.>

TN253

A

1001-5051(2017)03-0275-06