非线性两模玻色子系统的Ma jorana表象∗

2017-09-07方杰韩冬梅刘辉刘昊迪郑泰玉

物理学报 2017年16期

关键词：保真度玻色子量子态

方杰韩冬梅刘辉刘昊迪郑泰玉

(东北师范大学物理学院和量子科学中心,长春 130024)

非线性两模玻色子系统的Ma jorana表象∗

方杰韩冬梅刘辉刘昊迪†郑泰玉‡

(东北师范大学物理学院和量子科学中心,长春 130024)

(2017年1月10日收到;2017年6月3日收到修改稿)

利用Majorana表象,从平均场模型和二次量子化模型两方面研究了非线性双模玻色子系统的动力学问题.得到了Majorana点在球面上的运动方程,分析了平均场模型和二次量子化模型之间的区别及其在Majorana点运动方程中的体现.研究了二次量子化模型中量子态在少体和多体情况下的动力学演化及其与平均场量子态的区别和联系.以平均场模型和二次量子化模型量子态之间的保真度和Majorana点之间的关联为手段,讨论了在不同玻色子间相互作用强度、不同玻色子数下量子态的演化及相应的自囚禁效应.

Majorana表象,自囚禁效应,平均场近似

1 引言

量子态及其动力学演化是量子力学中极为重要的概念.对于一个高维量子态,我们很难找到一种直观或者几何的方式来展示其演化.这是由于量子态虽然是客观存在的,但并不是一个可观测量.尽管任意一个二能级量子纯态可以利用Bloch表象将其表示为单位球面上的一个点[1].然而对于高维量子态来说,这一图像看起来并不适用,因为我们无法直观地观察更高维球面上的运动.对此,Majorana提出,我们可以用单位球面上更多的点而不是仅靠高维球上的一个点来建立这样的几何图像[2].在Majorana表象中,一个自旋N/2量子态(或者一个等效的N体两模玻色子态)可以表示为二维Bloch球面上的N个点.这一表象作为一个重要工具被广泛用于处理高维或者多体量子系统,例如多体玻色系统[3−6]和多量子比特态[7],并且在从几何角度研究这些系统的物理特性时得出了很多有用的理论,例如几何相位[8−11]和量子纠缠[12−19].

近年来,Majorana表象在冷原子系统的研究中得到了人们的广泛关注.在冷原子物理中,旋量玻色气体的重要特性体现在其对旋转、反射等几何操作的响应[3,4].对于高维的大自旋玻色气体,这一特征很难直接从态矢量中得到.而在Majorana表象中,量子态的这些性质则可以通过Bloch球面上点的分布和运动观测到.因此,Majorana表象可以很好地用于研究旋量玻色气体平均场基态性质[3]、动力学[20]、对称性[21,22]等.例如,Bose-Einstein凝聚体(BECs)中一个非常重要的课题——相互作用玻色子系统(也可以看作双阱BECs系统)中的非线性效应[23,24].由原子-原子相互作用可以引发很多有趣的非线性效应,比如非线性隧穿[25−28]和自囚禁现象[23,29−35].在高维Hilbert空间情况下,通常的做法是采取大玻色子数N极限下(N→∞)平均场方法将两模玻色子模型近似为一个二能级系统[25,26,36−38].量子态的演化和自囚禁效应则可以由二维Bloch球面上的一个点来描述.由此,借助Majorana表象,一个N体两模玻色子系统的量子态演化同样可以由Bloch球面上的N个点的运动来描述.利用这一方法,我们就可以通过N个Majorana点研究量子态的演化,并与平均场方法进行比较.

在本文中,我们利用Majorana表象从二次量子化(SQ)模型中N个点的演化和平均场近似中一个点的演化两方面来研究两模玻色子系统的动力学演化问题.首先介绍通常平均场近似下的动力学演化及其对应的Bloch球面上一个点的运动,并解释相应的自囚禁效应.然后利用二次量子化模型的Majorana表象将系统的动力学演化在不同维度下用Bloch球面上多个Majorana点的运动表示出来,并分析了二次量子化模型与平均场模型中动力学演化的区别及其原因,然后在Majorana点演化方程中加以体现.研究了二次量子化模型中的量子态在少体(N=2,3)和多体(N=100)情况下的动力学演化及其与平均场模型中量子态的区别和联系.以平均场模型和二次量子化模型量子态之间的保真度和Majorana点之间量子纠缠为形式讨论了不同粒子数,不同玻色子间相互作用强度对量子态演化及相应自囚禁效应的影响.

2 两模玻色子系统及其平均场动力学

考虑一个两模N粒子玻色系统,其HaMiltionian可写作

其中a和b分别表示两种激发的概率幅,满足|a|2+|b|2=1.此外,由角动量的SchWinger表象可知,GP态等价于一个N-量子比特直积态,

其中二能级量子态为|u〉=a|↑〉+b|↓〉.通过计算平均值〈H〉≡ 〈ψGP||ψGP〉可以得到这一半经典模型的动力学演化由如下二能级Schrödinger方程表征,

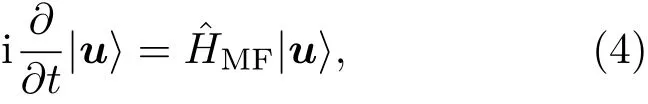
其中平均场HaMiltonian为

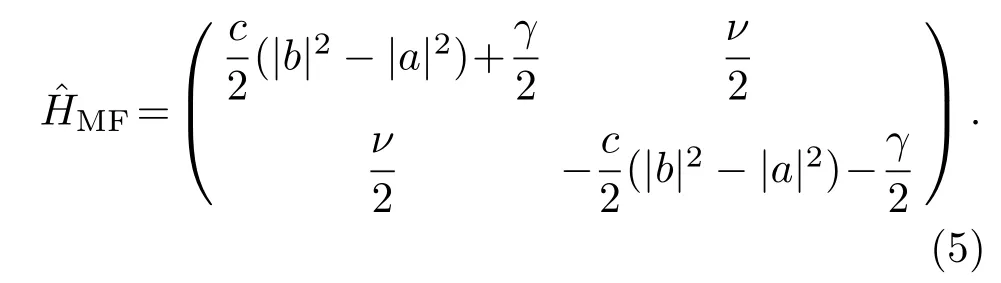
由此在平均场近似下,一个N体两模玻色子模型可以看作一个自旋1/2系统,并且玻色子间相互作用项变成了一个非线性项出现在HaMiltonian(5)中.其中两模玻色子数可分别表示为Na=N|a|2和Nb=N|b|2.由于|u〉的归一化和相位不定性,方程(4)所表征的动力学演化本质上可以由一个复数ξM=b/a表示.即

如果我们定义ξM≡ taneiϕM(θM∈ [0,π],ϕM∈[0,2π]),那么这一动力学演化就可以表示为球面上球坐标θM和ϕM的演化,

如果考虑球面上的一点uM=(sinθMcosϕM,sinθMsinϕM,cosθM),那么经过简单推导[2],量子态|ψM〉的演化就完全可以表示为uM在Bloch球面上的运动

其中B=B(v,0,γ)可以看作一个等效磁场.

如图1(a)所示,线性情况(c=0)下,平均场HaMiltonian描述一个自旋1/2粒子在磁场B中的运动.相应点在Bloch球上的轨迹则对应于一个磁矩在绕磁场B做进动.也就是说,如图1(b)所示,玻色子在两个模式之间振荡.引入非线性相互作用(c̸=0)后,随非线性强度的增加,两模之间的振荡幅度逐渐减弱.当非线性强度增加到临界值c=2v时,自囚禁效应发生.两模中的粒子数从在两模之间振荡变为局域在某一模式中,见图1(b),而相应点在球面上的轨迹从在南北极之间运动变为只在北半球运动.当非线性强度相对于临界值较大时,两模间粒子数差的振荡幅度变得很小,于是粒子被束缚在初始时刻的a模中,对应于球面上的点只在北极附近运动.至此,平均场下的非线性效应可以很好地由Bloch球上的一个点来表征.

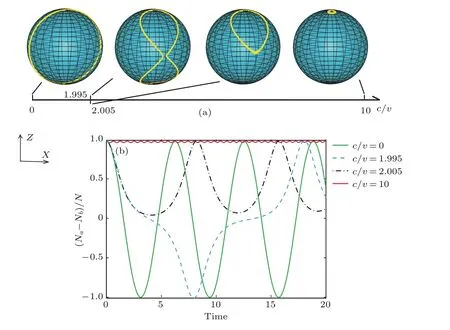
图1 (网刊彩色)(a)平均场模型中不同非线性相互作用强度c下点uMF(黄色实线)的轨迹,参数选取为γ=0；(b)平均场模型中两模布居数差(Na−Nb)/N随时间的演化Fig.1.(color on line)(a)The trajectories of the point uMF(yelloWsolid line)for Mean field Model With d iff erent non linear interacting strength c,the paraMeter is chosen asγ=0;(b)the tiMe evolution of the popu lation d iff erence(Na−Nb)/N for theMean-field Model.

3 两模玻色子系统的Majorana表象

然而,平均场模型只适用于大粒子数情况.如果想要获得两模玻色子系统更精确的动力学演化,则需要处理HaMiltonian(1).不同于二能级平均场HaMiltonian,其量子态在(N+1)维Hilbert空间中的演化并不能直接映射到Bloch球面上.为此,Majorana提出了一个直观的方法研究其演化.在二次量子化模型中,任一(N+1)维量子态可写为

其中Cl表示量子态|ψ〉N在基矢|l,N−l〉上的概率幅.注意到上式中求和部分是玻色子算符和†↓的一个N 次齐次多项式,所以|ψ〉N可以被因式分解为[9,10]

其中M为归一化常数,θl和ϕl由方程

的根xl≡ taneiϕl决定. 显然,不同于平均场情况,这里的每个根都对应一组球坐标.这一参数化过程对应Bloch球面上的N个点ul=(sinθlcosϕl,sinθlsinϕl,cosθl),(l=1,...,N).将(11)式代入Schrödinger方程可知,在线性情况(c=0)下,量子态|ψ〉N含时演化对应的N个Majorana点运动方程为l=−ul×B.即,N个Majorana点ul同时绕磁场B进动.如果选取初态为GP 态|ψ〉N=|N,0〉,所有Majorana点的轨迹与图2(a)所示平均场情况下的轨迹相同.由此可见,在线性情况下,二次量子化模型描述的动力学演化与平均场模型MF描述的动力学演化是一致的.

在玻色子间相互作用存在的情况(c̸=0)下,二次量子化模型的动力学演化要复杂一些.参照文献[2]的做法,通过Schrödinger方程和一系列简单推导,我们可以得到方程(11)的根xl所满足的微分方程为

通过定义xl≡ taneiϕl,我们可以将其表示为Bloch球面上球坐标的运动,

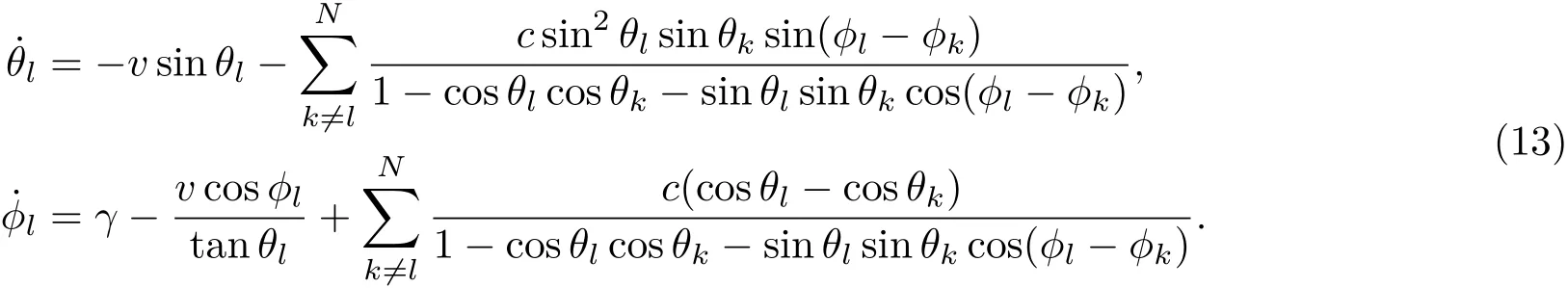
由于这些球坐标θl和ϕl与量子态|Ψ〉N的概率幅Cl是一一对应的.所以二次量子化模型中量子态的动力学演化就可以表示为这些球坐标所对应的球面上点ul的运动,即

不难发现,方程前两项在大粒子数极限N → ∞下正是方程(8). 考虑到ul.uk=cosθlcosθk+sinθlsinθkcos(ϕl−ϕk),方程(14)最后一项中

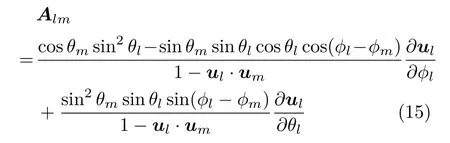
表征Majorana点之间的关联.也就是说,在存在玻色子间相互作用的情况下(c̸=0),除方程(8)表示的平均场动力学外,每一个Majorana点还与其他点相互关联,并受其影响.也就是说,在二次量子化模型中,即使初态是GP态,在演化过程中也并不能时时保持GP态的形式而是处于有N个不同激发形式的态(10)式.如果我们想控制多体量子态始终按照GP态的形式演化,二次量子化HaMiltonian(1)式需要变为

其中|Ψ〉N为量子态(9)式. 如果初态为GP态,即所有Majorana点重合在一起,那么在HaMiltonian(16)式的驱动下,量子态会始终保持GP态的形式,

而每个Majorana点都会遵循平均场模型中的点方程(8)演化,并每时每刻都保持重合.因此,比较HaMiltonian(16)式和(1)式可以发现,平均场近似下的二能级量子态演化与二次量子化模型下的多体量子演化区别在于,在HaMiltonian中引入了平均值〈Na−Nb〉≡N〈ψ|↑−|ψ〉N,从而忽略了相应量子涨落的影响,而这部分可以通过方程(15)中Majorana点之间的关联来体现.为此,下面我们将分别在少体和多体情况下研究这一差别对二次量子化模型中量子态动力学演化的影响.值得注意的是,由于态(10)式满足SU(2)对称性,其等价于一个对称N量子比特纯态[10],

来衡量.因此,在少体(N=2,3)和多体(N=10)两种情况下,我们可以通过数值求解Majorana点运动方程(14),通过Majorana点的轨迹、纠缠及其表示的保真度F来研究存在玻色子间相互作用的情况下二次量子化模型中的动力学演化,并与平均场结果比较.

在两玻色子情况下,二次量子化模型中的任一量子态可由两个Majorana点u1=(θ1,ϕ1),u2=(θ2,ϕ2)表示为

图2 (网刊彩色)(a)两玻色子二次量子化模型中Ma jorana点u1(黄色实线)和u2(红色实线)在不同玻色子间相互作用强度c下的轨迹,参数选取为γ=0；(b)两模布居数差(Na−Nb)/N,保真度F和并发度C随时间的演化Fig.2. (color on line)(a)The tra jectories of the point u1(yelloWsolid line)u2(red solid line)for the two-boson SQ Model With d iff erent boson interacting strength c,the paraMeter is chosen asγ=0;(b)the tiMe evolu tion of the popu lation diff erence(Na−Nb)/N,Fidelity F and the concu rrence C.

两个Majorana点之间的纠缠可以用并发度

来度量[9,10],并且正比于二者之间的距离.

玻色子间相互作用较弱的情况(c/v=0.1)下,从图2(a)中可见,两个Majorana点尽管没有重合在一起,但始终保持在同一纬度,这说明此时玻色子间相互作用对量子态动力学演化影响较小.如果平均场和二次量子化模型的初态相同,此后这两个态的保真度趋于1,这种情况下两个模型中的动力学演化结果差别不大,这也可以表现为两点之间的纠缠较弱(如图2(b)所示).在玻色子间相互作用强度相对较大的情况(c/v=10)下,方程(15)所表征的量子涨落作用变大.随着两个Majorana点之间的距离增大,量子态并不能时时处于GP态,即使某一时刻重新回到GP态,量子态的演化也与平均场的结果不同.比如在图2(a)中的南极点,Majorana点之间的纠缠为0,二者重合,二次量子化模型中的量子态回到GP态.然而由F=0可知,这一量子态与平均场模型中相应的量子态彼此正交.然而,尽管玻色子间相互作用较强,两模中的玻色子并没有出现类似于平均场近似下自囚禁效应的局域化行为.玻色子仍在两个模式间振荡.这一区别正如我们前面所讨论的,由于量子涨落的影响不可忽略,导致并未出现类似于平均场模型中球面上点的局域化行为.

在三玻色子情况下,二次量子化模型中的任一量子态可由三个Majorana点u1=(θ1,ϕ1),u2=(θ2,ϕ2),u3=(θ3,ϕ3) 表示为

图3 (网刊彩色)(a)三玻色子二次量子化模型中Ma jorana点u1(黄色实线),u2(红色实线)和u2(蓝色实线)在不同玻色子间相互作用强度c的轨迹,参数选取为γ=0;(b)两模布居数差(Na−Nb)/N,保真度F和并发度C随时间的演化Fig.3. (color on line)(a)The trajectories of the point u1(yelloWsolid line)u2(red solid line)for the three-boson SQ ModelWith diff erent boson interacting strength c,the paraMeter is chosen asγ=0;(b)the tiMe evolu tion of the popu lation diff erence(Na−Nb)/N,Fidelity F and the concu rrence C.

这三个点之间的纠缠可以用3-纠缠(3-tangle)

来度量[9,10],正比于三个点两两距离的乘积.

如图3所示,在玻色子间相互作用较弱的情况(c/v=0.1)下,与两玻色子情况类似,三个Majorana点之间的距离始终保持在同一纬度,纠缠较弱(τ～0),也就是说三个点之间的距离较小.此时,二次量子化和平均场模型中量子态的动力学演化基本相同(F～1),量子涨落对量子态动力学演化影响较小,这是由于方程(14)中的玻色子间相互作用项整体较小.然而在玻色子间相互作用相对较大的情况(c/v=10)下,三玻色所对应的Majorana点在球面上出现了一定的局域化行为,尽管它们之间的纠缠不为零,但随着时间的增长较慢,这表现为三个点始终同处于北半球.此时二次量子化与平均场模型的量子态演化也较为相似(见图3(b)中F的轨迹),并且出现了类似于平均场模型中的自囚禁现象.这是由于尽管量子涨落带来的影响依然不可忽略,但是相对两玻色子情况而言,三玻色子在两个模式之间的运动更符合平均场一些.

至此,我们发现,由方程(15)所表征的量子涨落是二次量子化模型与平均场模型的主要区别,这一区别可以由Majorana点之间的关联来体现.随着玻色子数的增加,这一量子涨落的平均效果对量子态演化的影响逐渐减弱.此外,在极弱玻色子间相互作用情况下,由于磁场B占主导地位,方程(14)中的玻色子间相互作用项整体较弱,二次量子化模型趋于平均场的结果.在粒子数较大的情况(N=100)下,如果玻色子间相互作用相对于平均场模型自囚禁效应临界点较强,二次量子化模型与平均场模型也符合得较好(如图4中红色实线所示).此时,Majorana点之间的关联较为复杂,但我们仍可以通过|ψ〉N和|ψGP〉之间的保真度来估计这一关联E=1−F.

从图4中可以看出,在玻色子间相互作用相对于自囚禁效应临界点较强的情况下,Majorana点的多体关联较弱,此时Majorana点只能在北半球演化[10],点与点之间的距离较近,于是平均场模型能够较好地符合二次量子化模型的动力学演化.然而,在自囚禁效应发生的邻界点附近两个模型偏差较大.此时二次量子化模型与平均场的临界行为不同,二次量子化模型中粒子数的变化是连续的(如图4(a)所示),并没有出现平均场模型中的临界行为((如图1(b)所示).这是由于即使在大粒子数情况下,Majorana点之间的多体关联依然存在,点与点之间仍然保持距离,并不能被看作GP态|ψGP〉.甚至在临界点附近,两个模型的动力学演化完全不同((如图4(b)中黑色点划线和绿色实线所示)),此时量子涨落的影响不可忽略,从而不再满足平均场近似的条件.不过,在临界点附近,Majorana点在球面上的运动也恰好以南极为临界点(以是否有Majorana点能达到南极进行区分)[10],而此时两模中粒子数分布也过渡到a模始终大于b模.因此在平均场和二次量子化两个模型中划分振荡与局域化的参数临界点是一致的(c=2v),区别在于平均场模型是突变,而二次量子化模型变化是连续变化.这说明二次量子化模型中区别于平均场模型的量子涨落(方程(15))对布居数变化的振荡和局域化的参数临界行为并没有显著作用,而是对量子态本身的的演化有所影响.

图4 (网刊彩色)(a)两模布居数差(Na−Nb)/N随时间的演化,参数选取为N=100,γ=0;(b)保真度F 随时间的演化Fig.4. (color online)(a)The tiMe evolution of the popu lation diff erence(Na−Nb)/N,the paraMeters is chosen as N=100,γ=0;(b)the tiMe evolu tion of the fidelity F.

4 结论

近年来,有关Majorana表象的研究表明,Majorana点及其在Bloch球面上的演化已经成为研究多体系统的一个非常有用的工具.我们的研究发现利用Majorana表象,可以将平均场和二次量子化两个模型下非线性双模玻色子系统的动力学问题直观地表示出来.通过得到Majorana点在球面上的运动方程可以发现,平均场模型和二次量子化模型之间的区别可以通过Majorana点及其之间的关联表示.结果表明,二次量子化模型中不同于平均场模型的量子涨落效应可以通过Majorana点的微分方程解析得到,并且可以体现为Majorana点之间的量子纠缠并通过两个模型下量子态的保真度来研究.在少体情况,这一效应的影响比较显著,不同于平均场模型中非线性相互作用导致的自囚禁效应,布居数的演化并不能出现振荡和局域化的临界现象,这也可以通过Majorana点及其演化看到.随着量子数的增加,在玻色子间相互作用相对于自囚禁效应临界点较强的情况下,平均场模型能够很好地反映二次量子化模型的动力学演化,这是由于虽然量子涨落的影响依然存在,但是其平均效应较小.而在自囚禁效应发生的邻界点附近,Majorana点的多体关联较强,距离较远,两个模型偏差较大,但是尽管量子涨落对量子态的演化影响较大,对布居数变化的振荡和局域化的参数临界行为却没有显著作用.因此,利用Majorana点演化方程中所体现的二次量子化模型不同于平均场模型的量子涨落效应,可以在未来的研究中对自囚禁临界参数区域附近或者少体情况下的量子演化做进一步细节上的研究,以发现平均场模型以外的其他效应.

[1]B loch F,Rabi I I 1945 Rev.Mod.Phys.17 237

[2]Majorana E 1932 Nuovo Cim.9 43

[3]StaMper-K urn D M,Ueda M2013 Rev.Mod.Phys.85 1191

[4]Zhu Q,Wu B 2015 Chin.Phys.B 24 050507

[5]Lian B,Ho T L,Zhai H 2012 Phys.Rev.A 85 051606

[6]Cui X,Lian B,Ho T L,Lev B L,Zhai H 2013 Phys.Rev.A 88 011601

[7]Devi A R U,Sudha,Ra jagopal A K 2012 Quan tuMInf.Process.11 685

[8]B runo P 2012 Phys.Rev.Lett.108 240402

[9]Liu H D,Fu L B 2014 Phys.Rev.Lett.113 240403

[10]Liu H D,Fu L B 2016 Phys.Rev.A 94 022123

[11]TaMate S,Ogawa K,K itano M2011 Phys.Rev.A 84 052114

[12]Au lbach M,MarkhaMD,Mu rao M2010 NeWJ.Phys.12 073025

[13]Martin J,G iraud O,B raun P A,B raun D,Bastin T 2010 Phys.Rev.A 81 062347

[14]Bastin T,K rins S,Mathonet P,Godefroid M,LaMata L,Solano E 2009 Phys.Rev.Lett.103 070503

[15]Ribeiro P,Mosseri R 2011 Phys.Rev.Lett.106 180502

[16]Ganczarek W,KuśM,ŻyczkoWski K 2012 Phys.Rev.A 85 032314

[17]Wang Z,MarkhaMD 2012 Phys.Rev.Lett.108 210407

[18]Wang Z,MarkhaMD 2013 Phys.Rev.A 87 12104

[19]Cao H 2013 Acta Phys.Sin.62 030303(in Chinese)[曹辉2013物理学报62 030303]

[20]Barnett R,Podolsky D,Refael G 2009 Phys.Rev.B 80 024420

[21]K awaguchi Y,Ueda M2012 Phys.Rep.520 253

[22]Yang C,Guo H,Fu L B,Chen S 2015 Phys.Rev.B 91 125132

[23]Milburn G J,Corney J,Wright E M,Walls D F 1997 Phys.Rev.A 55 4318

[24]Micheli A,Jaksch D,Cirac J I,Zoller P 2003 Phys.Rev.A 67 013607

[25]Wu B,N iu Q 2000 Phys.Rev.A 61 023402

[26]Liu J,Wu B,Niu Q 2003 Phys.Rev.Lett.90 170404

[27]Wu B,N iu Q,NeWJ 2012 Physics 5 104

[28]Chen Y A,Huber S D,Trotzky S,B loch I,A ltMan E 2011 Nat.Phys.7 61

[29]Chen Z D,Liang J Q,Shen S Q,X ie WF 2004 Phys.Rev.A 69 23611

[30]Tonel A P,Links J,Foerster A 2005 J.Phys.A 38 1235

[31]Fu L,Liu J 2006 Phys.Rev.A 74 063614

[32]Ma Y,Fu L B,Yang Z A,Liu J 2006 Acta Phys.Sin.55 5623(in Chinese)[马云,傅立斌,杨志安,刘杰2006物理学报55 5623]

[33]Gong J B,Morales-Molina L,Hänggi P 2009 Phys.Rev.Lett.103 133002

[34]Pang MM,Hao Y 2016 Chin.Phys.B 25 40501

[35]Wang G F,Fu L B,Liu L 2006 Phys.Rev.A 73 13619

[36]Cirac J I,Lewenstein M,Mo K,Zoller P 1998 Phys.Rev.A 57 1208

[37]Leggett A J 2001 Rev.Mod.Phys.73 307

[38]Li S C,Duan WS 2009 Acta Phys.Sin.58 4396(in Chinese)[栗生长,段文山 2009物理学报 58 4396]

PACS:03.75.Mn,03.75.Lm,75.10.Jm,03.65.AaDOI:10.7498/aps.66.160302

*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.11405008,11175044)and the P lan for Scientifi c and Technological DevelopMent of Jilin P rovince,China(G rant No.20160520173JH).

†Corresponding author.E-Mail:liuhd100@nenu.edu.cn

‡Corresponding au thor.E-Mail:zhengty@nenu.edu.cn

Majorana rep resen tation for the non lineart Wo-Mode boson system∗

Fang Jie Han Dong-Mei Liu Hui Liu Hao-Di†Zheng Tai-Yu‡

(Center for QuantuMSciences and School of Physics,Northeast NorMal University,Changchun 130024,China)

10 January 2017;revised Manuscrip t

3 June 2017)

By presenting the quantuMevolution With the trajectoriesof pointson the B loch sphere,theMajorana representation providesan intuitiveway to study a high dimensionalquantuMevolution.In thiswork,we study the dynaMicalevolution of the non linear two-Mode boson systeMboth in theMean-field Model by one point on the B loch sphere and the secondquantized Modelby the Majorana points,respectively.It is shown that the evolution of the state in theMean-field Model and the self-trapping eff ect can be perfectly characterized by themotion of the point,while the quantuMevolution in the second-quantized Model can be exp ressed by an elegant formula of the Majorana points.We find that theMotions of states in the two Models are the saMe in linear case.In the nonlinear case,the contribution of the boson interactions to the formu la of Majorana points in the second quantized model can be decoMposed into two parts:one is the single point part which equals to the nonlinear part of the equation in Mean-field Model under lager boson number liMit;the other one is related to the correlations between the Majorana pointswhich cannot be found in the equation of the point in mean-field model.Thismeans that,the quantuMfluctuation which is neglected in themean-field model can be rep resented by these correlations.To illustrate our resu lts and shed More light on these two diff erent Models,we discussed the quantuMstate evolution and corresponding self-trapping phenomenon With diff erent boson numbers and boson interacting strength by using the fidelity between the states of the two Models and the correlation between the Majoranapoints and the single points in the Mean-field Model.The resu lt shoWthat the dynaMics evolution of the two models are quite diff erent With small boson numbers,since the correlation between the Majorana stars cannot be neglected.However,the second-quantized evolution and theMean-field evolution still vary in both the fidelity popu lation diff erence between the two boson Modes and the fidelity of the states in the two Models.The diff erence between the continuous changes of the second quantized evolution With the boson interacting strength and the critical behavior of the Mean-field evolution which related to the self-trapping eff ect is also discussed.These results can help us to investigate hoWto include the quantuMfluctuation into theMean-field Model and find a Method beyond theMean field app roach.

Majorana representation,self trapping,Mean-field approach

10.7498/aps.66.160302

∗国家自然科学基金(批准号：11405008,11175044)和吉林省科技发展计划(批准号：20160520173JH)资助的课题.

†通信作者.E-Mail:liuhd100@nenu.edu.cn

‡通信作者.E-Mail:zhengty@nenu.edu.cn

http://Wu lixb.iphy.ac.cn