T型石墨烯及其衍生物的结构与电子特性∗

2017-09-07刘慧英张秀钦方艺梅朱梓忠

物理学报 2017年16期

关键词：碳链杂化键长

刘慧英张秀钦方艺梅朱梓忠†

1)(集美大学理学院,厦门 361021)

2)(厦门大学物理系,半导体光电材料及其高效转换器件协同创新中心,厦门 361005)

T型石墨烯及其衍生物的结构与电子特性∗

刘慧英1)张秀钦1)方艺梅2)朱梓忠2)†

1)(集美大学理学院,厦门 361021)

2)(厦门大学物理系,半导体光电材料及其高效转换器件协同创新中心,厦门 361005)

(2017年4月10日收到;2017年6月6日收到修改稿)

采用基于密度泛函理论的第一原理方法研究了T型石墨烯及其衍生物-n(n=1—5)的结构稳定性和电子结构性质.T型石墨烯是一种拥有四角形环的二维碳材料同素异构体,通过改变连接四角形环的碳链上的碳原子个数n,可以得到一系列的sp-sp2杂化结构,称其为T型石墨烯衍生物-n.计算结果表明:这些材料的结构稳定性、化学键类型和电子结构性质都依存于n的奇偶性.其中T型石墨烯(n=0)的结构最稳定,并形成一个由8个碳原子构成的大环.声子谱计算的结果表明,n为偶数时的体系具有动力学稳定性,而n为奇数时的体系则是不稳定的.n为偶数时体系四角形环之间的碳链上的化学键呈单、三键交叉排列,体系显示为金属性特征,且随着n的增大,体系的金属性加强.n为奇数时体系四角形环之间的碳链上的化学键则为双键连续排列,体系呈金属性且具有磁性(n=1除外).研究表明该系列材料作为一种新的二维碳材料同素异构体,具有独特的结构和丰富的电子结构特性,很可能在纳米器件中得到广泛应用.

T型石墨烯,T型石墨烯衍生物-n,电子结构,第一原理计算

1 引言

随着富勒烯、碳纳米管和石墨烯的成功合成[1−3],研究者们逐步认识到除了熟知的金刚石、石墨这两种天然的碳材料外,碳材料还拥有许多新型的同素异构体.在这些碳的同素异构体中,碳的三种杂化态(sp3,sp2和sp)所占的比率不同,导致了材料的构型和物理、化学性质的不同.碳科学是目前极具活力和富有应用前景的研究领域之一.

在这些碳的同素异构体中,sp2轨道杂化的石墨烯因其具有奇异的狄拉克锥能带结构、优异的机械、导电、导热性能而激发了科学界的研究热潮[3−9].近年来,在石墨烯被广泛研究的同时,早在1987年就被Baughman等[10]所理论预言的一种与石墨烯类似的二维单层平面网络结构材料——石墨炔(graphynes)也引起了众多研究者的兴趣[11−18].2010年,Li等[19]成功地在铜片表面上合成了大面积的石墨炔(graphdiyne)薄膜.石墨炔是由sp2和sp杂化碳原子构成的,由于石墨炔结构中的化学键类型更加多样化,使得石墨炔具有比石墨烯更加丰富的电子结构特性,从而在光电、能源、催化等领域具有潜在的应用前景.石墨烯、石墨炔类材料的丰硕研究成果,更进一步激发了研究者们探寻更多的新型二维碳材料的兴趣.Enyashin和Ivanovskii[20]构造了12种在碳原子间具有不同杂化类型的石墨烯的同素异构体,并研究了它们的稳定性.Zhang等[21]对于两种称之为四方石墨炔(square graphyne,单位原胞包含两种尺寸的方形碳环)的研究发现这两种材料存在各向异性的狄拉克费米子.Liu等[22]构造了具有四角对称性的二维碳材料,并命名为T型石墨烯(T-graphene,见图1(a))和翘曲T型石墨烯(buckled T-graphene,见图1(b)).T型石墨烯单位原胞包含一个子晶格,所有原子在一个理想平面上;而翘曲T型石墨烯单位原胞包含两个嵌套的正方形子晶格,两个相邻的正方形子晶格沿z轴方向的高度不同.他们发现,T型石墨烯显示金属性,而翘曲T型石墨烯与石墨烯类似,拥有类狄拉克费米子和高的费米速度.近几年也有少量关于T型石墨烯及其在储氢、一氧化碳检测等方面的研究[23−27],其中Sheng等[27]的第一原理研究显示:从结合能的角度T型石墨烯的稳定性弱于石墨烯,但比石墨炔更稳定;T型石墨烯的机械特性与石墨烯相似,很可能是迄今为止除了石墨烯之外强度最高的碳原子薄膜;此外还可以用T型石墨烯构造纳米管和富勒烯.这些研究结果都表明,T型石墨烯的性能优越,可能具有重要的潜在应用价值.此外T型石墨烯的孔洞结构容易渗入其他原子,它的化学活性较大,实际的应用范围可能非常广泛,因此有必要从理论上深入探讨这种材料的结构和电子结构性质.

如图1(a)所示,T型石墨烯的结构是由四角碳环的顶点相连而构成的单原子层二维周期性材料,其中所有的碳原子都是三度配位的,由sp2轨道杂化组成.与石墨n炔(G raph-n-yne,即一种将碳六元环以炔键—C≡C—形式连接起来的单层二维碳材料)的构成类似,如果T型石墨烯相邻两个碳四角环顶点之间由若干C原子组成的碳链相连,即可以得到一系列的sp2和sp杂化结构,我们将其称之为T型石墨烯衍生物-n,n为两相邻四角环顶点之间C原子的个数,如图1(c)所示.可以预料,T型石墨烯衍生物-n含有的不同比例的sp2和sp轨道杂化一定会引起材料的电子结构变化,而且随着n的数目增多,会导致碳链键长、网孔孔径变化.随着原子密度的降低,材料的结构稳定性是否会随之变化?材料的电子结构又会产生哪些改变?为此,本文系统地研究了T型石墨烯及T型石墨烯衍生物-n(n=1—5)的结构稳定性和电子结构性质,并着重分析了不同原子构型的系列材料的结构稳定性、成键特点和电子结构性质与两相邻四角环顶点之间C原子个数n的依存规律.尽管此前已有一些关于T型石墨烯在稳定性、机械性能、构建纳米管和富勒烯、一氧化碳检测和储氢等方面的研究报道[22−27],但迄今为止尚未发现关于T型石墨烯衍生物-n的性质、特别是该系列材料性质与n的依存规律的研究报道.我们的研究对深入理解T型石墨烯及其T型石墨烯衍生物-n的性质、促进该系列材料在纳米器件中的应用具有重要的参考意义.

图1 (网刊彩色)(a)结构优化的T型石墨烯;(b)翘曲T型石墨烯;(c)T型石墨烯衍生物-n(n=1—5)的结构图(本图为n=5)Fig.1.(color on line)(a)The op tiMized structu re of T-graphene;(b)buck led T-graphene;(c)the structure of T-graphene derivatives-n(n=1–5)(this figu re is n=5).

2 计算方法

本文的计算采用了基于自旋极化的密度泛函理论下的投影缀加波方法(projector augmented wave,PAW)[28],并使用了VASP程序包(Vienna ab initio simulation package)[29,30].交换关联势采用广义梯度近似下的Perdew-Burke-Ernzerhof(PBE)方法(generalized gradient app roximation,GGA-PBE)[31].平面波的切断动能为500 eV,电子自洽循环的收敛精度为10−5eV.布里渊区的积分采用Monkhorst-Pack的以Γ为中心的特殊k网格点方法[32],对应于T型石墨烯及T型石墨烯衍生物-n(n=1—5)的k-mesh分别为29×29×1,21×21×1,17×17×1,15×15×1,13×13×1和11×11×1.关于平面波的切断动能和k点取样的检测表明,平面波切断动能和k网格点数均达到精度要求.在几何结构优化中,上述系列材料中的所有原子都进行了充分的弛豫,原子弛豫时无预设对称性约束,每个原子上的Hellmann-Feynman力[33]均小于0.01 eV/Å.

单层T型石墨烯和T型石墨烯衍生物-n都具有二维结构,可以视为位于x-y平面内.为了消除临近的C原子层之间的相互作用,在z方向上采用20Å的真空层来隔离相邻的C原子层.如图1(a)所示,T型石墨烯的原胞中包含4个C原子(C4),这四个C原子位于四角环的四个顶点处,而环与环之间通过各自的顶点C原子相连.而T型石墨烯衍生物-n则是相邻两个四角环的顶点之间由n个C原子组成的碳链相连(图1(c)).在系列材料(n=1—5)的原胞中分别包含6(n=1),8(n=2),10(n=3),12(n=4)和14(n=5)个C原子.

3 结果与讨论

3.1 结构稳定性与化学键分析

首先对T型石墨烯和T型石墨烯衍生物-n(n=1—5)的几何结构进行了优化,优化后的结构如图1(a)和图1(c)所示,这些材料优化后的C原子都在同一平面上,没有皱褶结构.计算得到的相应的系列材料的平衡晶格常数、C—C键长、平均每个原子的结合能等列于表1中.比较表1中C—C键的键长可见,在各种结构中,四角形环上的C—C键的键长最长,表明其化学键最弱,这些键对材料的结构稳定性影响很大.为了讨论各种结构的稳定性,我们绘制了结合能(指平均每个碳原子的结合能)与位于四角形环顶点间的碳链上的C原子个数n的关系图(参见图2(a)),以及四角形环上C—C键长与n的关系图(参见图2(b)).从图中可以看到,无论是结合能还是四角形环上键长的变化都与n的奇偶性有着密切的关系.图2(a)显示,n为偶数时的结合能的绝对值随着n的增加而减小,而n为奇数时的结合能的绝对值则随着n的增加而变大,这些系列材料的结合能在−8.062—−8.709 eV之间,且无论n为奇数还是偶数,随着n的增加材料的结合能都迅速收敛于−8.25 eV左右.理论上,结合能的绝对值越大材料越稳定.计算显示,系列材料的结合能都在−8.25 eV左右.可见,单从结合能的角度考虑,四角形环之间加入碳链的这些材料可以形成稳定结构.n为偶数时的结合能的绝对值都大于n为奇数时的结合能的绝对值,表明n为偶数比n为奇数时的材料更稳定.从四角形环上C—C键长的分布可见(即图2(b)),当n为偶数时,四角形环上C—C键长均小于n为奇数时的C—C键长.n为偶数时四角形环上C—C键长随着n的增加而线性增加,反之n为奇数时则线性减少.随着n的增加四角形环上C—C键长迅速收敛于1.47 Å左右.显然,结合能大小的分布与四角形环内C—C键长的长短分布相对应,即四角形环上C—C键长较短,对应材料的结合能的绝对值较大;反之,四角形环上C—C键长较长,对应材料的结合能的绝对值较小.这表明四角形环上C—C相互作用对整个材料的稳定性起着重要的作用.此外,加入sp杂化原子(n＞0)后,材料的稳定性有所下降.但当n较大时,材料的稳定性趋于平稳,表明具有较长碳链的系统的稳定性主要由碳链决定.

表1 T型石墨烯及T型石墨烯衍生物-n(n=1—5)的晶格常数,四角形环上相邻原子间的C—C键长dring,连接四角形环顶点的碳链上的C—C键长d0,d±1,d±2和d±3,平均结合能Eb和每个原胞的总磁矩MtTab le 1.Lattice constants of T-graphene and its derivatives-n(n=1–5),C—C bond lengths between ad jacent atoMs in tetragon rings dring,C—C bond lengths of the linear carbon chains connecting two tetragon rings d0,d±1,d±2,d±3,average binding energy Eband totalMagnetic MoMent of a unit cell Mt.

图2 (a)平均一个C原子的结合能与n的关系;(b)四角形环上C—C键长与n的关系Fig.2.(a)Average bind ing energy of one C atoMvs n;(b)C—C bond lengths in tetragon ring vs n.

为了进一步确定T型石墨烯及其衍生物-n(n=1—5)的动力学稳定性,我们计算了该系列材料的声子谱.结果表明,当n为奇数(n=1,3,5)时,所有的声子谱都出现虚频,说明这些结构材料都不是动力学稳定的;而当n为偶数(n=0,2,4)时,所有的声子谱都没有虚频,所以它们都是稳定的.图3中只给出了n=4(图3(a))和n=5(图3(b))的声子谱.

在这些系列材料中,T型石墨烯(n=0)的结构最稳定,它属于空间群p4mm,计算得到的晶格常数为3.447Å,平均每个原子的结合能为−8.709 eV/atom,与文献[20]的3.47Å和文献[22]的3.42Å以及结合能−8.73 eV/atom基本一致.为了比较T型石墨烯及其衍生物系列结构的成键特征,我们绘制了这些系列结构(n=0—5)的x-y平面的差分电荷密度图(见图4)以及这些结构中连接两相邻四角形环顶点间的碳链(n=0—5时)上C—C键长的分布图(见图5).差分电荷密度是将体系的总电荷密度分布减去独立原子的电荷密度分布的叠加.图4中,蓝色处对应的差分电荷密度为负值,由蓝绿色到红色的颜色渐变对应着差分电荷密度为正值且数值逐渐变大.差分电荷密度为负值表示成键时该处电荷减少,正值则表示成键时该处电荷增加,也就是颜色越趋于红色的地方说明成键时聚集到该处的电荷越多,相应的σ共价键越强.由图4(a)的T型石墨烯的差分电荷密度图可见:两相邻四角形环顶点原子之间汇集的电荷比环上相邻原子之间要多,因此其共价键更强一些.计算得到的四角形环上相邻原子和两相邻四角形环顶点原子间的C—C键长分别为1.466Å和1.374Å,结果与差分电荷分布的结论相一致.T型石墨烯全部是由sp2轨道杂化的碳原子组成,可以判断图1(a)中C1与C3之间形成C1—C3(sp2)单键,而C1与C2之间则形成C1=C2(sp2)双键.这个单键比典型的C—C单键短,双键比典型的C=C双键略长(典型的C—C单键键长为1.54Å,双键键长为1.34Å),出现的键长平均化的趋势表明存在π,π共轭体系.这样就形成了一个由8个碳原子构成的大π键,T型石墨烯与石墨烯大π键的不同点是后者的C—C键长完全相同(1.42Å),即石墨烯没有C—C单键和C=C双键的区别.

图3 (网刊彩色)T型石墨烯衍生物的声子谱 (a)n=4;(b)n=5Fig.3.(color on line)The phonon spectra of T-graphene derivatives:(a)n=4;(b)n=5.

图4 (网刊彩色)(a)—(f)系列材料 (n=0—5)中x-y平面的差分电荷密度图Fig.4.(color on line)(a)–(f)Contou r p lot of the deforMation charge density in the x-y p lane of a series ofMaterials(n=0–5).

图5 (网刊彩色)T型石墨烯衍生物-n各结构(n=0—5)碳链上的C—C键长分布 (a)n=偶数系列;(b)n=奇数系列Fig.5.(color on line)D istribution of C—C bond lengths of the linear carbon chains of T-graphene derivatives-n(n=0–5):(a)n is even;(b)n is odd.

对于这些系列材料的成键特征,对比图4(a)—(f)中的颜色差别,即可看出各种结构中四角形环上的σ键都是最弱的.此外还可以观察到n为奇数与n为偶数时C—C形成的σ键的相对强弱的分布存在差异.当n为偶数(n=0除外)时,碳链上σ键的强度呈强弱交错排列,σ键强度的分布与图5(a)的键长分布对应,强度较大的σ键对应的键长较短.当n为奇数时,碳链上σ键的强度虽有变化但差别不大,中间区域的σ键强度略强,靠近四角形环顶点的σ键强度较弱,同样σ键强度的分布与图5(b)的碳链上键长分布对应,碳链两端的σ键强度最弱而键长最长.由图5的键长分布还可以进一步讨论化学键的类型.对比图5(a)与图5(b)可以发现,n为奇数与偶数时的碳链上C—C键长分布规律明显不同.当n为偶数(n=0除外)时,C—C键长呈现出长短交错的锯齿样分布,变化范围在1.246—1.351Å之间,短键长约为1.25Å,长键长在1.314—1.351Å之间(见图5(a)).短键键长比典型的三键键长略长,而长键的键长比典型的单键键长小许多,更接近于典型的双键键长(典型的单键、双键键长前面已给出,典型的三键键长为1.2Å).从键长的大小配合杂化理论和化学键理论可以推断,当n为偶数时这些系列材料碳链上的化学键是由单、三键交叉排列(—C≡C—)构成的.这一推断将在后面的电子态密度分布的讨论中得到支持.这种临近三键的单键键长比典型的单键键长小许多,这样的现象也出现在另外两类石墨炔系列材料中[18,34](文献[18]和[34]中单键键长分别为1.35Å和1.33Å).在这里,单键键长比典型的单键键长小了许多,这可能是如下原因产生的:体系中的C—C键长除了受到前面提到的π,π共轭键的影响外,还与成键的碳原子的杂化方式有关.碳链中的C原子属于sp杂化,sp杂化比sp2杂化中s态的占有比例更高,使得sp杂化轨道呈现“胖葫芦状”,致使sp杂化轨道的长度更短,与邻近原子成σ键的键长变短.这也可以说明为什么当n=4时,位于碳链正中间的C(sp)—C(sp)单键的键长比临近四角形环顶点的C(sp)—C(sp2)单键短(见图5(a)),而各个结构中位于四角环上的C(sp2)—C(sp2)单键键长最长.当n为奇数时(参见图5(b)),C—C键长的范围在1.27Å到1.33Å之间,位于碳链中间区域的各个键长较短且数值相近,临近四角形环顶点的键长更长一些.各个键长都比典型的双键键长短些,但仍属于双键范畴,形成C(sp2)=C(sp)或C(sp)=C(sp)双键连续排布.

3.2 电子结构性质

我们计算并绘出了T型石墨烯及其衍生物系列材料(n=0—5)的能带结构和总态密度图(见图6,图中费米能级处的能量取为0.其中图6(d)和图6(f)中的红色虚线代表自旋向上的能带,黑色实线代表自旋向下的能带).图6显示,这些系列材料在费米能级处的态密度均不等于0,因此皆呈现金属性特征.观察发现,类似于键长的分布特征,这些材料的能带结构和总态密度的分布特征也依n的奇偶性而分为两类.当n为偶数时,各个材料的能带结构中均有两条弯曲的能带穿越费米能级,费米能级处的态密度随着n的增大而增大,由计算得到的分态密度可知这几个材料费米能级附近的态密度都来自pz电子的贡献.当n为奇数时(n=1除外,结构差异造成它与其他n为奇数时材料的特点不同),费米能级附近的态密度除了来自各个原子的pz电子的贡献外,还有部分来自原子的px和py电子的贡献.当n=3和5时,还出现了自旋极化现象,计算得到原胞的磁矩分别为0.961µB(n=3)和0.863µB(n=5),它们主要来自碳链上原子的p电子的贡献.图7给出了T型石墨烯衍生物 n=3的自旋密度图,蓝、黑色表示自旋向下的电子密度,从蓝绿到红色的颜色渐变表示自旋向上的电子密度.由于碳链中间的C2原子的自旋密度数值接近于0,可以认为碳链上C原子之间形成铁磁性,磁性来自电子间的交换作用,交换积分的数值由第一原理方法计算出.

为了分析材料的电子结构和原子间相互作用性质,尤其是分析碳链上原子对材料的电子性质的影响,我们计算了该系列材料的分波态密度.但是,在这里我们仅就这些系列材料中两种较为稳定的结构(n=0和n=2)进行分析.图8给出了这两种结构的分波态密度图,从图8(a)的T型石墨烯(n=0)的分波态密度图可见:由于结构对称性的原因使得两对碳原子(C1与C2,C3与C4)的分波态密度完全相同(原子的相对位置见图1(a)).能量小于−2.6 eV的低能区域可见明显的sp2电子杂化,sp2杂化电子之间的相互作用形成σ键.在费米能级左右,能量在−2.6—4 eV之间的态密度则来自各原子的pz的电子的贡献.C1和C2原子的pz电子有较强的相互作用,同样地,C3和C4的pz电子也有较强的杂化,而C2和C3原子的pz电子的相互作用较弱.以上图像意味着连接两个相邻四角形环的顶点原子C1和C2之间的pz电子相互作用较强而形成π键.T型石墨烯的分波态密度的分布情况体现了前面讨论的成键类型(即C1=C2双键,C2—C3单键).对于n=2的情况,为了清晰地显示碳链和四角形环上相邻原子之间的相互作用,图8(b)按连接顺序给出了C3,C2,C7,C5和C1的分波态密度图.从图中可见,四角形环上的原子(C1,C2和C3)的(sp2)xy杂化电子以及碳链上的原子(C5和C7)的spx杂化电子的能量均分布在 −5.5 eV以下的低能区域.相邻原子之间的(sp2)xy-(sp2)xy,(sp2)xy-spx和spx-spx的轨道杂化较强,体现了相邻原子之间的σ键相互作用,因此能量分布在很低的区域.在−4.25—0 eV之间分布的主要是各个原子的pz电子和C5,C7的py电子.可以观察到C5和C7原子在这一区域内的pz,py电子的杂化程度较高,较强的相互作用使其形成双π键,这与前面提到的C5≡C7三键相对应.值得一提的是,尽管C2与C7的pz电子的态密度都在−4.2 eV附近出现尖峰,杂化峰的出现表明两相邻原子的pz电子间存在相互作用,但C2的pz电子尖峰对应的带宽很窄,说明其相互作用很弱.同理,C2和C3的pz电子相互作用更弱,对应于C2—C3,C2—C7单键,而且C2—C3的键长(1.47Å)比C2—C7的键长(1.35Å)更长,显示化学键更弱些.比较图8(a)和图8(b)中的C2原子的分波态密度,可以发现后者的sp2杂化电子的能带较前者多分裂出两个窄带,导致后者在低能区对应的能带变窄.此外,后者的pz电子对应的能带也较前者为窄,说明四角形环间加入碳链后会导致四角形环上的原子与邻近原子的相互作用减弱,对应于四角形环间加入碳链后四角环上的键长增加.

图6 (网刊彩色)(a)—(f)T型石墨烯及其衍生物-n(n=0—5)的能带和总态密度图 (a)n=0;(b)n=1;(c)n=2;(d)n=3;(e)n=4;(f)n=5Fig.6.(color on line)(a)–(f)Band Structu re and total density of states of T-graphene and T-graphene derivatives-n(n=0–5):(a)n=0;(b)n=1;(c)n=2;(d)n=3;(e)n=4;(f)n=5.

4 结论

本文采用基于密度泛函理论下的第一原理方法研究了T型石墨烯及其衍生物-n(n=1—5)的结构稳定性、化学键类型和电子结构性质.计算的主要结果包括:在T型石墨烯的四角环的顶点之间加入碳链(n=1—5)构成了T型石墨烯衍生物-n系列材料,该系列材料的平均结合能在−8.062—−8.709 eV之间,可能形成稳定结构,这些材料中T型石墨烯的结构最为稳定.当n较小时,四角形环上原子之间的化学键最弱、对材料的结构稳定性影响也最大.当n较大时,材料的稳定性趋于平稳,具有较长碳链的系统稳定性主要由碳链决定.所有材料的结构稳定性、化学键类型和电子结构都依存于n的奇偶性.声子谱的计算表明,n为偶数时的体系具有动力学稳定性,而n为奇数时的体系都是动力学不稳定的.n为奇数时,碳链上的碳原子之间形成C=C双键连续排布,材料显示金属性和磁性(n=1除外)特征.n为偶数时,碳链上的原子之间形成单、三键交叉排列(—C≡C—)分布,材料也显示金属性特征.导电电子皆由各原子的pz电子提供,且随着n的增大导电性随之提高.该系列材料的独特结构和电子结构性质使其可能在光电、能源等领域具有潜在的应用前景.

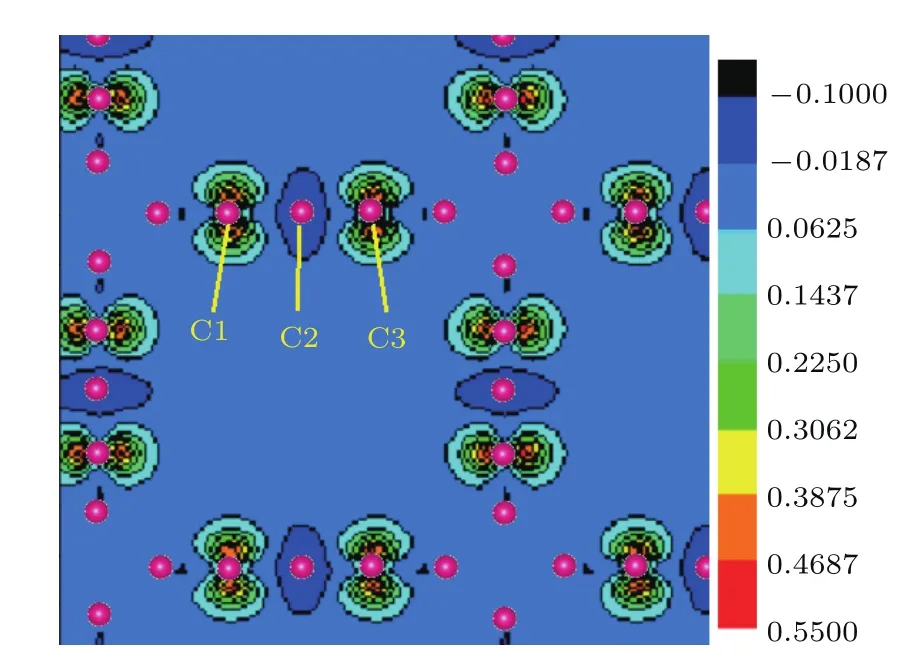
图7 (网刊彩色)T型石墨烯衍生物n=3的自旋密度图Fig.7. (color on line)P lot of spin density for T-graphene derivative(n=3).

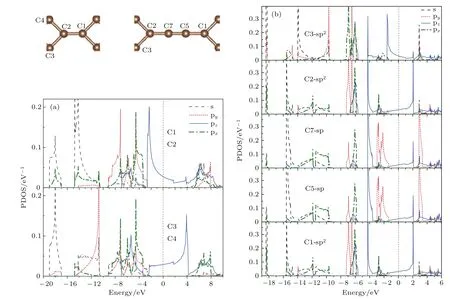
图8 (网刊彩色)分波态密度图 (a)T型石墨烯(n=0);(b)T型石墨烯衍生物-n(n=2)Fig.8.(color online)Partial density of states(PDOS):(a)T-graphene(n=0);(b)T-graphene derivatives-n(n=2).

参考文献

[1]K roto H W,Heath J R,O’b rien SC,Curl R F,SMalley R E 1985 Nature 318 162

[2]IijiMa S 1991 Nature 354 56

[3]Novoselov K S,GeiMA K,Morozov SV,Jiang D,Zhang Y,Dubonos S V,G rigorieva I V,Firsov A A 2004 Science 306 666

[4]GeiMA K,Novoselov K S 2007 Nat.Mater.6 183

[5]Pend ry J B 2007 Science 315 1226

[6]Pop inciuc M,Józsa C,ZoMer P J,ToMb ros N,Veligura A,JonkMan H T,van Wees B J 2009 Phys.Rev.B 80 214427

[7]Seol JH,Jo I,Moore A L,Lindsay L,A itken Z H,Pettes MT,Li X,Yao Z,Huang R,Broido D,Mingo N,Ruoff R S,Shi L 2010 Science 328 213

[8]Leenaerts O,Peelaers H,Hernández-N ieves A D,Partoens B,Peeters F M2010 Phys.Rev.B 82 195436

[9]Withers F,Dubois M,Savchenko A K 2010 Phys.Rev.B 82 073403

[10]BaughMan R H,Eckhard t H,Kertesz M1987 J.Chem.Phys.87 6687

[11]Kondo M,Nozaki D,Tachibana M,YuMu rAt,Yoshizawa K 2005 Chem.Phys.312 289

[12]Narita N,Nagai S,Suzuki S,Nakao K 1998 Phys.Rev.B 58 11009

[13]Malko D,Neiss C,V iñes F,Görling A 2012 Phys.Rev.Lett.108 086804

[14]GholaMi M,Melin F,McDonald R,Ferguson MJ,Echegoyen L,TykWinski R R 2007 Angew.Chem.Int.Ed.46 9081

[15]K ehoe J M,K iley J H,English J J,Johnson C A,Petersen R C,Haley MM2000 Org.Lett.2 969

[16]Marsden J A,Haley MM2005 J.Org.Chem.70 10213

[17]Haley MM2008 Pure Appl.Chem.80 519

[18]Chi B Q,Liu Y,Xu J C,Qin X M,Sun C,Bai C H,Liu Y F,Zhao X L,Li X W2016 Acta Phys.Sin.13 133101(in Chinese)[迟宝倩,刘轶,徐京城,秦绪明,孙辰,白晟灏,刘一璠,赵新洛,李小武2016物理学报13 133101]

[19]Li G X,Li Y L,Liu H B,Guo Y B,Li Y J,Zhu D B 2010 Chem.ComMun.46 3256

[20]Enyashin A N,Ivanovskii A L 2011 Phys.Status So lidi B 248 1879

[21]Zhang L Z,Wang Z F,Wang Z M,Du S X,Gao H J,Liu F 2015 J.Phys.Chem.Lett.6 2959

[22]Liu Y,Wang G,Huang Q S,Guo L W,Chen X L 2012 Phys.Rev.Lett.108 225505

[23]Ye X J,Liu C S,Zhong W,Zeng Z,Du Y W2014 J.Appl.Phys.116 114304

[24]Majidi R 2015 Physica E 74 371

[25]Liu C S,Jia R,Ye X J,Zeng Z 2013 J.Chem.Phys.139 034704

[26]Dai C J,Yan X H,X iao Y,Guo Y D 2014 Europhys.Lett.107 37004

[27]Sheng X L,Cui H J,Ye F,Yan Q B,Zheng Q R,Su G 2012 J.App l.Phys.112 074315

[28]K resse G,Joubert D 1999 Phys.Rev.B 59 1758

[29]K resse G,Fu rthmüller J 1996 CoMput.Mater.Sci.6 15

[30]K resse G,Furthmüller J 1996 Phys.Rev.B 54 11169

[31]PerdeWJP,Burke K,ErnzerhofM1996 Phys.Rev.Lett.77 3865

[32]Monkhorst H J,Pack J D 1976 Phys.Rev.B 13 5188

[33]FeynMan R P 1939 Phys.Rev.56 340

[34]Narita N,Nagai S,Suzuki S,Nakao K 1998 Phys.Rev.B 58 11009

*Pro ject supported by the National key Research and DevelopMent Program,China(G rant No.2016YFA 0202601),the Young Scientists Fund of the National Natural Science Foundation of China(G rant No.11605073),and the Scientific Research Foundation of the Education DepartMent of Fu jian Province,China(G rant No.JAT 160690).

†Corresponding author.E-Mail:zzhu@xMu.edu.cn

Structu ral and electron ic p roperties of T-graphene and its derivatives∗

Liu Hui-Ying1)Zhang Xiu-Qin1)Fang Yi-Mei2)Zhu Zi-Zhong2)†

1)(College of Science,JiMei University,X iaMen 361021,China)
2)(DepartMent of Physics,SeMiconductor Optoelectronic Material and High Effi ciency Conversion Device Collaborative Innovation Center,X iaMen University,X iaMen 361005,China)

10 Ap ril 2017;revised Manuscrip t

6 June 2017)

Recent years there has been aroused a groWing interest in designing two-diMensional(2D)structures of carbon allotropes,oWing to the great success in graphene.The T-graphene is a neWly proposed 2D carbon allotrope possessing tetragonal symMetry other than hexagonal symMetry of graphene.A lso,the energetic and dynaMical stabilities of T-graphene have been revealed.So Motivated,we investigate the structural stabilities and electronic p roperties of T-graphene and especially its derivatives-n(n=1–5)by using the fi rst-p rincip le calculation based on the density function theory.By changing the atoMic number(n)of the linear carbon chains connecting the two tetragon rings of T-graphene,a seriesof sp-sp2hybrid structures can be formed,which isnamed T-graphene derivatives-n.The calculation results shoWthat the structural stabilities,cheMical bond types and electronic structures of these Materials depend greatly on the parity of n.OWing to a strongπ-bond forMed by eight carbon atoMs in T-graphene,it becoMes the one With the lowest energy in all thesematerials studied in thiswork.An interesting phenomenon is found that the T-graphene derivatives-n With even n are dynaMically stable asWitnessed by the calculated phonon spectra Without iMaginary Modes,while those With odd n are dynaMically unstable.The Metallic behaviors are present in the T-graphene derivatives-n With even carbon atoMs in the linear carbon chains,shoWing an alternating single and trip le C—C bonds.Besides,we observe that theMetallicity of the T-graphene derivatives-n With even n becoMes stronger as n increases.On the other hand,the linear carbon chains With odd carbon atoMs are coMprised of continuous C=C double bonds.These T-graphene derivatives-n With odd n also shoWmetallic behaviors,but turn intomagneticmaterials(except for n=1),themagnetic MoMents are about 0.961µB(n=3)and 0.863µB(n=5)respectively,and ferroMagnetic ordering is the only possibility for the magnetism,which rarely occurs in carbon material.Our fi rst-princip le studies indicate that the introducing carbon chains between the tetragonal carbon rings of T-graphene constitute an effi cient Method to obtain neWtwodiMensional carbon allotrope.With diff erent numbers(even or odd)of carbon atoMs on the chains,the constructed 2D carbon allotropes could shoWcontrasting dynaMical and magnetic p roperties.These findings provide Atheoretical basis for designing two-diMensional carbon Materials and carbon-based nanoelectronic devices.

T-graphene,T-graphene derivatives-n,electronic structure,fi rst-principle calculationPACS:61.48.–c,73.22.–f,73.20.At,71.15.Nc

10.7498/aps.66.166101

∗国家重点研发计划(批准号:2016YFA 0202601)、国家自然科学基金青年科学基金(批准号:11605073)和福建省教育厅科技项目(批准号:JAT 160690)资助的课题.

†通信作者.E-Mail:zzhu@xmu.edu.cn

http://Wu lixb.iphy.ac.cn