火灾环境液化石油气卧罐动态可靠性分析

贾梅生，陈国华

（华南理工大学安全科学与工程研究所，广东 广州 510640）

火灾环境液化石油气卧罐动态可靠性分析

贾梅生，陈国华

（华南理工大学安全科学与工程研究所，广东 广州 510640）

沸腾液体扩展蒸汽云爆炸（BLEVE）是液化烃介质压力容器处于火灾环境而极易发生的一类多米诺效应灾难事故。在火灾环境液化石油气（LPG）卧罐两节点集中温度参数模型基础上，基于随机扩散过程和首次穿越失效理论，对其动态可靠性进行建模与分析。集中温度参数模型通过转化为一个二维伊藤随机微分方程，得到漂移与扩散系数表达式；根据首次穿越失效理论，定义条件动态可靠性函数，导出函数满足的后向柯尔莫哥洛夫方程（KBE）；应用有限差分法并结合适当边界条件求解KBE，得到动态可靠性结果。与静态可靠性不同，动态可靠性方法可描述整个时间轴的破坏失效可能性，为多米诺效应定量风险评价提供更可靠、更精确的概率结果。

沸腾液体扩展蒸汽云爆炸；多米诺效应；火灾；液化石油气；动态可靠性；首次穿越失效；后向柯尔莫哥洛夫方程

沸腾液体扩展蒸汽云爆炸（BLEVE）与多米诺效应密切相关[1-8]，当前已有许多实验与理论研究[9-16]，以揭示BLEVE机理、预测事故后果影响或验证安全措施有效性。多米诺效应定量风险评价使用的比例方法[1-2]或Probit模型[3-4]一般较少考虑BLEVE动力学过程，静态可靠性方法也无法描述系统未达稳定状态就已破坏失效的可能性。

针对液化石油气（LPG）卧罐，在两节点集中温度参数模型基础上，基于随机扩散过程和首次穿越失效理论[17-19]，对其处于火灾环境时的动态可靠性进行建模与分析。

1 模型与方法构建

1.1 集中温度参数模型

使用火灾环境LPG卧罐稳定性与静态可靠性分析时构建的两节点集中温度参数模型[20]，微分方程如式(1)。

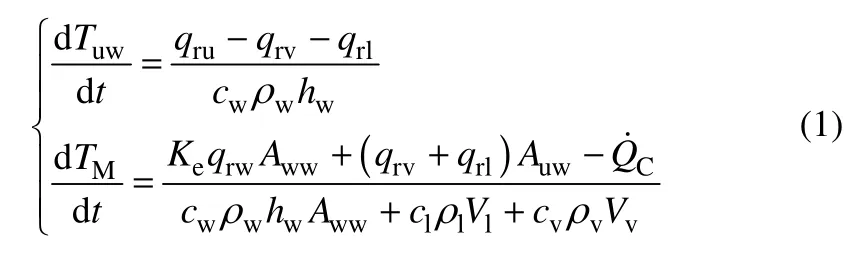
1.2 伊藤随机微分方程

根据扩散过程理论[19]，式(1)可建模为二维扩散过程，干壁温度Tuw(t)与共享温度TM(t)为系统随机响应。设火焰外表面温度Tf(t)为系统随机激励，且为一维高斯白噪声，可表示为式(2)。

式中，E[·]为均值运算，当Tf(t)为平稳过程时，E[Tf(t)]为常数；N(t)为零均值高斯白噪声，强度为2D。

由于Tf仅以四次方形式出现于火灾对干壁、湿壁辐射换热热通量qru、qrw中，所以方程(1)首先需转化为如式(3)形式。

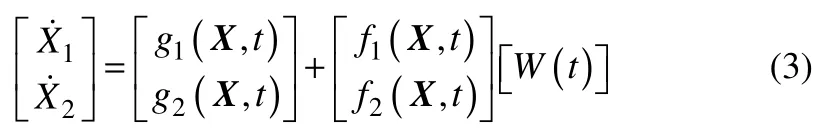
式中，X=[Tuw,TM]T；gi、fi是确定性函数；W(t)=[Tf(t)]4，也是一个零均值高斯白噪声，强度为2E，与2D的关系如式(4)。

式中，ΔTf、Δ(Tf4)分别是Tf、Tf4的偏差，2E、2D按工程经验取各自偏差的1/3。

确定性函数gi、fi形式如式(5)。

式中，x为X样本。

1.3 后向柯尔莫哥洛夫方程

假设在[0,t]内，当Tuw(t)超过Tcr（罐壁材料极限温度，K）或TM(t)超过Tcg（丙烷临界温度，K）至少一次时，LPG卧罐即发生首次穿越而破坏失效。定义条件可靠性函数如(9)。

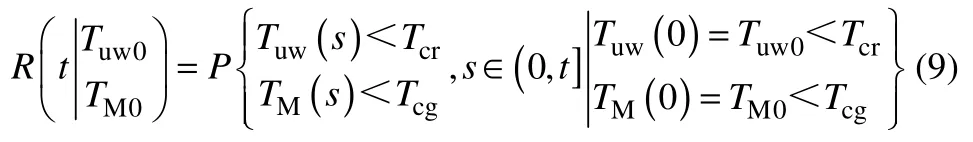
式中，Tuw0、TM0为初始温度变量。

R(·)满足的后向柯尔莫哥洛夫方程（KBE）如式(10)。

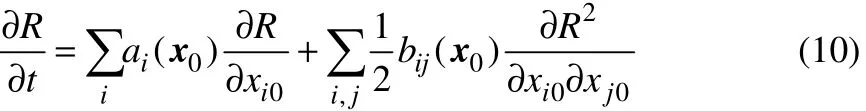
初始条件与边界条件如式(11)～式(13)。

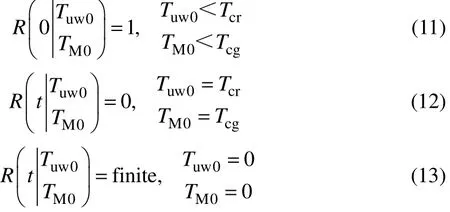
式(11)与式(12)不相容，理论上仅存在广义解，但对数值解没有影响。式(13)中，由于绝对0度不可达到，finite取值为1。另外，根据集中温度参数模型的破坏失效判断式，Tcr与TM相关，所以实际计算域是一个由Tuw0=0、TM0=0及Tcr曲线构成的封闭曲面，如图1所示。罐壁材料为TC-128，室温抗拉强度为560MPa，Tcr曲线两个端点由假设TM0=Tcg=369.83K和σθ（TM0）=S(Tuw0)=0MPa计算获得。

图1 动态可靠性计算域示意图

由于系统初始状态是给定的，且处于安全域，所以对应无条件量与条件量结果一致。另外，计算E(τ)时，模拟时间应足够长，使p(·)充分趋近于0。

1.4 有限差分法

式(10)～式(13)构成的抛物型偏微分方程是对流占优的，为减小数值震荡的影响，当a1(xi,xj)≤0且a2(xi,xj)≤0时，使用如式(17)迎风型差分格式，进行有限差分法数值计算[21]。

2 实例分析

以BRL现场实验为例进行分析计算[9]，表1是两节点集中温度参数模型的参数取值。破坏失效时间td=1426s，对应用时间平均算子后，取值如表2所示。由于计算域是三维的，网格数量对有限差分法数值运算效率影响很大，当网格Tuw0×TM0×t为118×74×481时，程序执行一次耗时约245min。

图2是破坏失效概率Pd的各种结果视图。可以看出：Pd存在一个上升的时间区间；Tuw0、TM0对该时间区间的大小与起始点影响很大；边界上Pd的变化趋势如图2(c)所示。

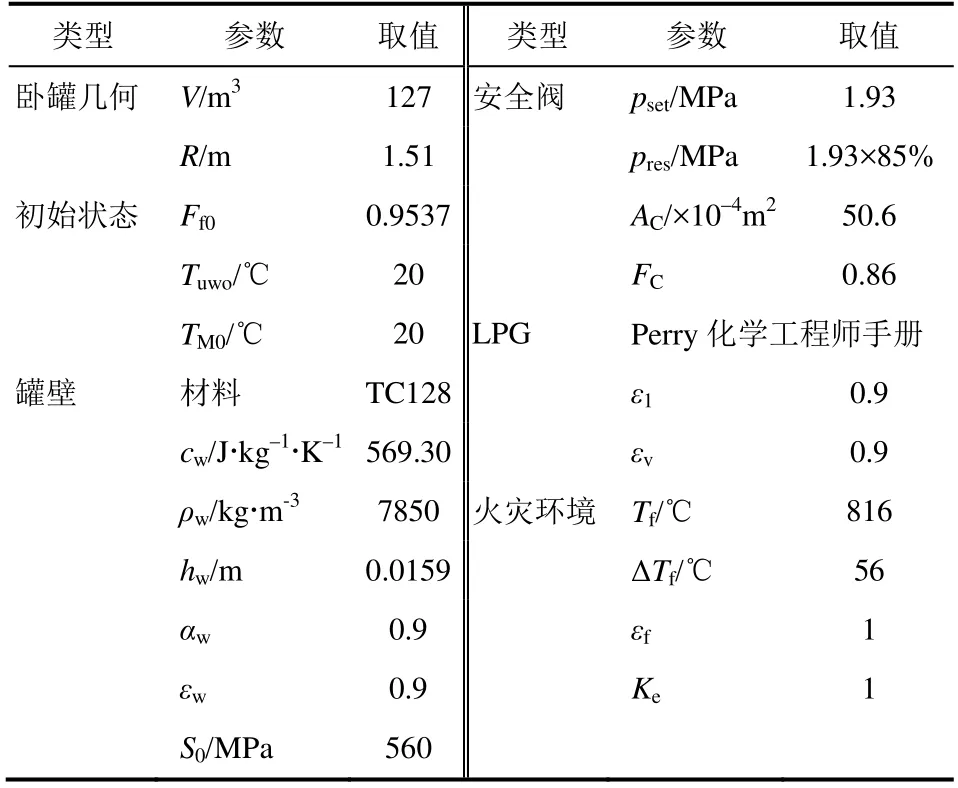
表1 模型参数取值

表2 时间平均值

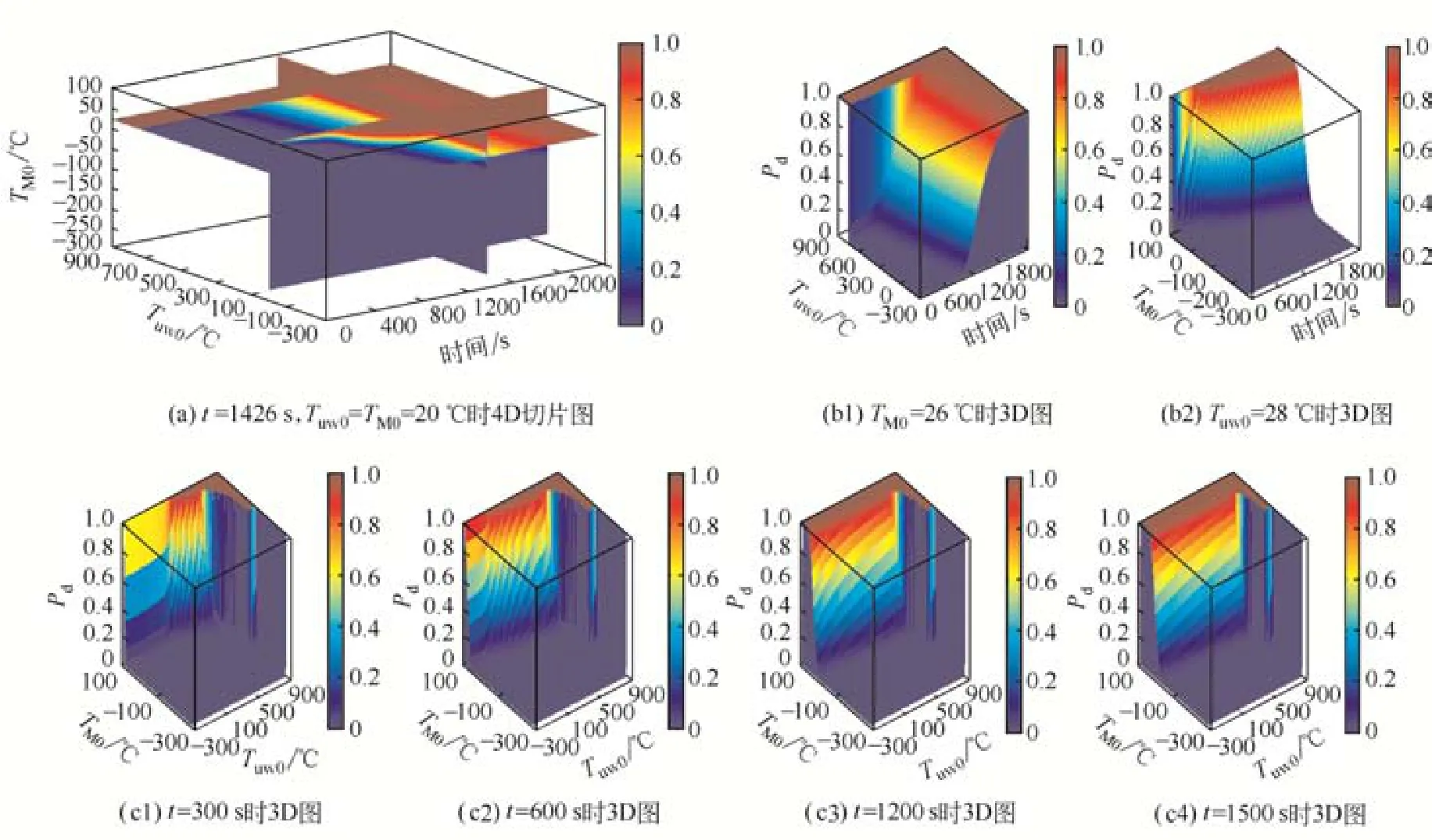
图2 破坏失效概率结果视图

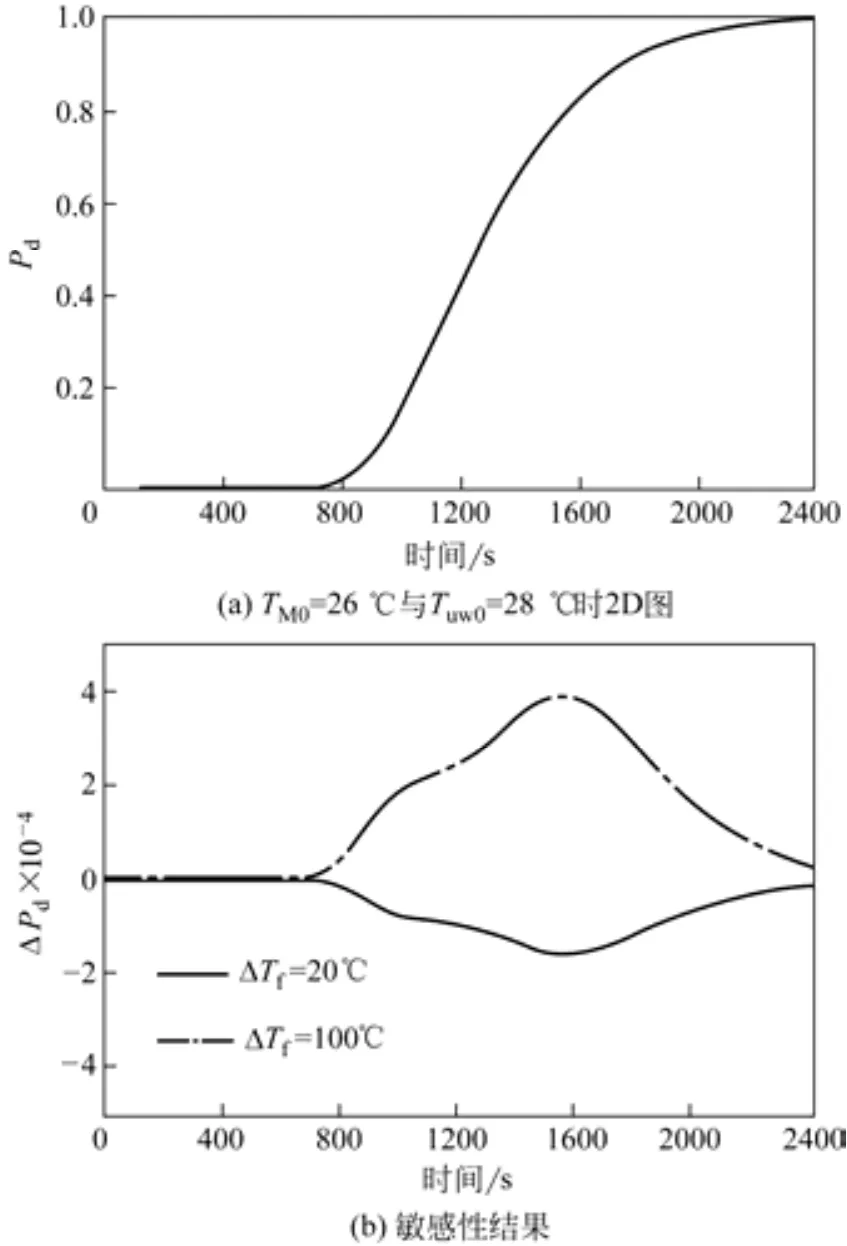
图3 破坏失效概率关于火焰温度偏差的敏感性

图3是指定TM0=26℃、Tuw0=28℃时，Pd关于ΔTf的敏感性结果。ΔPd表示相对于ΔTf=56℃时，Pd的增加量。可以看出：ΔTf影响是比较小的，数量级在10–5；ΔPd(t)呈近似半周期的正弦曲线形状，有别于理论预测的单周期，原因是模拟时间不够长，未能使Pd充分趋近于1，见图3(a)。

图4是平均首次穿越时间或平均寿命E(τ)与初始体系温度的关系。当近似从0℃增加到35℃时，E(τ)从1569s下降到1114s，主导因素是TM0，表明过热态比最大拉应力破坏失效更敏感。

图4 平均首次穿越时间

3 结论

（1）在两节点集中温度参数模型基础上，基于随机扩散过程和首次穿越失效理论，建模并表征火灾环境液化烃介质压力容器动态可靠性的方法是有效可行的，可描述整个时间轴的破坏失效可能性，可为多米诺效应定量风险评价提供更可靠、更精确的概率结果。

（2）BRL实例分析表明，其动态破坏失效概率存在一个明显的上升时间区间，初始体系温度对该时间区间的大小与起始点影响很大，火焰温度偏差的影响是比较小的，并且过热态比最大拉应力破坏失效更敏感。

符号说明

AC—— 安全阀流道面积，m2

Auw—— 干壁面积，m2

Aww—— 湿壁面积，m2

c1—— 饱和态丙烷液相比热，J/(kg·K)

cv—— 饱和态丙烷蒸汽相定压比热，J/(kg·K)

cw—— 罐壁比热，J/(kg·K)

FC—— 安全阀排量系数

Ff—— LPG体积充装系数

Frlv—— 干壁对液面视角系数

hw—— 罐壁厚度，m

Ke—— 火焰吞噬卧罐比例

pres—— 安全阀回座压力，MPa

pset—— 安全阀整定压力，MPa

—— 安全阀泄压释放热量速率，J/s

qrl—— 干壁对液相辐射换热热通量，W/m2

qru—— 火灾对干壁辐射换热热通量，W/m2

qrv—— 干壁对蒸汽相辐射换热热通量，W/m2

qrw—— 火灾对湿壁辐射换热热通量，W/m2

R—— 卧罐内半径，m

S—— 罐壁材料抗拉强度，MPa

Tcg—— 丙烷临界温度，K

Tcr—— 罐壁材料极限温度，K

Tf—— 火焰外表面温度，K

TM—— 蒸汽相、液相、湿壁共享节点温度，K

Tuw—— 干壁节点温度，K

td—— 破坏失效时刻，s

V—— 卧罐容积，m3

V1—— 液相体积，m3

Vv—— 蒸汽相体积，m3

αw—— 罐壁表面热辐射吸收率

εf—— 火焰热辐射发射率

ε1—— LPG液面热辐射发射率

εv—— LPG蒸汽相热辐射发射率

εw—— 罐壁表面热辐射发射率

ρ1—— 饱和态丙烷液相密度，kg/m3

ρv—— 饱和态丙烷蒸汽相密度，kg/m3

ρw——罐壁密度，kg/m3

σ—— 黑体辐射常数，5.67×10–8W/(m2·K4)σθ——罐壁周向应力，MPa

[1] MANNAN S. Lees’ loss prevention in the process industries：Hazard identification，assessment and control[M]. 3rd ed. Elsevier，2005.

[2] KHAN F I，ABBASI S A. Models for domino effect analysis in chemical process industries[J]. Process Safety Progress，1998，17（2）：107-123.

[3] COZZANI V，GUBINELLI G，ANTONIONI G，et al. The assessment of risk caused by domino effect in quantitative area risk analysis[J]. Journal of Hazardous Materials，2005，127（1/2/3）：14-30.

[4] KADRI F，CHATELET E，CHEN G P. Method for quantitative assessment of the domino effect in industrial sites[J]. Process Safety and Environmental Protection，2013，91（6）：452-462.

[5] 张新梅，陈国华. 化工罐区爆炸碎片多米诺效应影响概率计算模型[J]. 化工学报，2008，59（11）：2946-2953.ZHANG X M，CHEN G H. Impact probability of domino effect caused by explosion fragments in chemical tank area[J]. Journal of Chemical Industry and Engineering（China），2008，59（11）：2946-2953.

[6] 钱新明，徐亚博，刘振翼. 球罐BLEVE碎片抛射的Monte-Carlo分析[J]. 化工学报，2009，60（4）：1057-1061.QIAN X M，XU Y B，LIU Z Y. Monte-Carlo analysis of fragments projectile from spherical tank[J]. CIESC Journal，2009，60（4）：1057-1061.

[7] 孙东亮，蒋军成，张明广，等. 基于最大熵原理的卧罐爆炸碎片数量概率分布[J]. 化工学报，2011，62（s1）：219-224.SUN D L，JIANG J C，ZHANG M G，et al. Probabilistic distribution of fragments number from explosion of horizontal tank based on maximum entropy principle[J]. CIESC Journal，2011，62（s1）：219-224.

[8] HEMMATIAN B，PLANAS E，CASAL J. Fire as a primary event of accident domino sequences：the case of BLEVE[J]. Reliability Engineering & System Safety，2015，139：141-148.

[9] ANDERSON C，TOWNSEND W，ZOOK J，et al. The effects of a fire environment on a rail tank car filled with LPG[R]. Maryland：Ballistic Research Laboratories，1974.

[10] KIELEC D J，BIRK A M. Analysis of fire-induced ruptures of 400 L propane tanks[J]. Journal of Pressure Vessel Technology，Transactions of the ASME，1997，119：365-373.

[11] BIRK A M，VANDERSTEEN J D J. On the transition from non-BLEVE to BLEVE failure for a 1.8 m3propane tank[J]. Journal of Pressure Vessel Technology，Transactions of the ASME，2006，128：648-655.

[12] LANDUCCI G，MOLAG M，REINDERS J，et al. Experimental and analytical investigation of thermal coating effectiveness for 3 m3LPG tanks engulfed by fire[J]. Journal of Hazardous Materials，2009，161（2/3）：1182-1192.

[13] BIRK A M. Review of AFFTAC thermal model[R]. Kingston：Transportation Development Centre，2000.

[14] SALZANO E，PICOZZI B，VACCARO S，et al. Hazard of pressurized tanks involved in fires[J]. Industrial & Engineering Chemistry Research，2003，42（8）：1804-1812.

[15] MANU C C，BIRK A M，KIM I Y. Stress rupture predictions ofpressure vessels exposed to fully engulfing and local impingement accidental fire heat loads[J]. Engineering Failure Analysis，2009，16（4）：1141-1152.

[16] D'AULISA A，TUGNOLI A，COZZANI V，et al. CFD modeling of LPG vessels under fire exposure conditions[J]. AIChE Journal，2014，60（12）：4292-4305.

[17] GARDINER C W. Handbook of stochastic methods - For physics，chemistry and the natural sciences[M]. 2nd ed. Springer-Verlag，1996.

[18] 朱位秋. 随机振动[M]. 北京：科学出版社，1998.ZHU W Q. Random vibration[M]. Beijing：Science Press，1998.

[19] 朱位秋. 非线性随机动力学与控制——Hamilton理论体系框架[M]. 北京：科学出版社，2003.ZHU W Q. Nonlinear stochastic dynamics and control —A theoretical framework for Hamilton system[M]. Beijing：Science Press，2003.

[20] 贾梅生，陈国华. 火灾环境液化石油气卧罐稳定性与静态可靠性分析[J]. 化工进展，2017，36（7）：2353-2359.JIA M S，CHEN G H. Stability and static reliability of horizontal LPG tank exposed to fire[J]. Chemical Industry and Engineering Progress，2017，36（7）：2353-2359.

[21] 张文生. 科学计算中的偏微分方程有限差分法[M]. 北京：高等教育出版社，2006.ZHANG W S. Finite difference methods for partial differential equations in science[M]. Beijing：Higher Education Press，2006.

Dynamic reliability of horizontal LPG tank exposed to fire

JIA Meisheng，CHEN Guohua
（Institute of Safety Science and Engineering，South China University of Technology，Guangzhou 510640，Guangdong，China）

The liquefied hydrocarbon pressure vessel exposed to heat radiation from fire is extremely dangerous，which may incur the boiling liquid expanding vapor explosion（BLEVE）of disaster domino effect. In this paper，based on the established two-node lumped temperature model（LTM），the dynamic reliability of the horizontal LPG tank exposed to fire was researched by applying stochastic diffusion process（SDP）and first passage failure（FPF）theories to LTM. Firstly，the LTM was converted to a two-dimensional Ito stochastic differential equation（SDE）to obtain the expressions of drift and diffusion coefficient. Then，according to FPF，a conditional dynamic reliability function was defined and the Kolmogorov backward equation（KBE）that the defined function satisfied was derived. Finally，the dynamic reliability was obtained by solving the KBE using the finite difference method（FDM）with some reasonable boundary conditions. Being different from the static reliability method，the dynamic one could describe the damage probability in whole timeline so as to provide a more reliable and accurate probability result for quantitative risk assessment（QRA）of domino effect.

BLEVE；domino effect；fire；LPG；dynamic reliability；first passage failure；KBE

TQ086；X937

：A

：1000-6613（2017）09-3231-06

10.16085/j.issn.1000-6613.2016-1823

2016-10-09；修改稿日期：2017-01-10。

国家自然科学基金（21576102）及国家重点研究开发计划（2016YFC0801500）项目。

贾梅生（1988—），男，博士研究生。联系人：陈国华，教授，博士生导师，从事工业安全风险评价技术研究。E-mail：mmghchen@scut.edu.cn。