有机朗肯循环中的工质热源转折温度及其特征

李新国，王伟，翟哲，南来福，王竞逸

（天津大学机械工程学院，天津 300350）

有机朗肯循环中的工质热源转折温度及其特征

李新国，王伟，翟哲，南来福，王竞逸

（天津大学机械工程学院，天津 300350）

有机朗肯循环中存在有极值功循环与无极值功循环，即存在一种净功的转折线与所对应的工质热源转折温度，它对工质的选择与循环性能评价具有指标性的作用。基于梯形循环及其理论模型，本文建立工质饱和线形状（饱和液线斜率、饱和气线斜率及其斜率比与临界温度）及物性为自变量的数学关系，并提出和定义线性饱和线工质模型，建立循环性能与工质物性之间的数学关系。分别推导出有机朗肯循环中工质热源转折温度的经验公式，以及梯形循环下线性饱和线工质的热源转折温度理论公式及其修正。研究热源转折温度及其对应的优化工况的特征与一般性规律，得到21种工质热源转折温度的有机朗肯循环数值计算与经验公式之间的偏差小于1.97%。线性饱和线工质模型下，工质的热源转折温度为临界温度和蒸发器窄点温差之和；热源转折温度所对应的最高优化工况（最高优化蒸发温度与最大净功极值）随斜率比单调增加，至干工质时，最高优化工况接近工质的临界点。

有机朗肯循环；梯形循环；线性饱和线工质；工质热源转折温度；最高优化工况

有机朗肯循环（organic Rankine cycle，ORC）采用低沸点有机工质发电，可以回收利用300℃以下的中低温热能，如太阳能、地热能、工业余热等。目前ORC的研究一般是针对具体工质的数值计算或实验研究。徐荣吉等[1]以R245fa为工质，提出基于对数传热温差的内回热器性能计算方法，并分析过热温度、过冷温度对内回热ORC性能的影响，表明内回热减少了循环的蒸发负荷和冷凝负荷，提高了循环效率。韩中合等[2]针对烟气余热构建无回热和有内回热的ORC系统，通过热源参数变化引起工质吸热量的变化，分析工质在两种系统中的初温、净功量、热耗率及㶲损的变化规律，得出较优工质和各工质对内回热器的匹配性。杨绪飞等[3]在给定热源条件下，探讨进口过热度对膨胀机性能和系统性能的影响，表明随膨胀机进口过热度递减，膨胀机机械效率递增，等熵效率递减，膨胀机轴功和实际运行效率呈先增后减的变化趋势。王明涛等[4]建立能量平衡方程和㶲方程，研究蒸发压力对不同烷烃类工质的热效率、单位质量烟气净功、㶲效率等参数的影响规律，表明在保证膨胀机体积流量比不大于50情况下，环戊烷具有最高的热效率和㶲效率。张军辉等[5]以最大做功能力和㶲效率为目标函数，对10种工质进行分析，表明每种工质均存在一优化蒸发温度使循环净输出功最大，而且工质临界温度越高，对应的优化蒸发温度也越高。贺超等[6]采用不同优化目标，对亚临界ORC进行蒸发温度和冷凝温度的优化分析。在排烟温度423.15K条件下，对干工质，不同优化目标下蒸发温度和冷凝温度优化值差异较大；湿工质R134a与R152a临界温度低于热源初始温度20K±2K时，系统存在优化蒸发温度。LI等[7]在热源温度120～200℃下，对5种有机工质从安全、环保、经济效益方面进行分析，表明R123非常不安全，但它的热经济效率最高，尤其热源温度较高时。YU等[8]研究表明，当ORC系统在近临界温度区域内运行，即热源进口温度与工质临界温度之差在适当范围内时，系统可获得最大的输出功。

也有学者从理论角度对有机朗肯循环进行分析。最早由严家禄[9]对两种热源形式的ORC，分别推导了工质优化蒸发温度和冷却水温升的数学关系式和相应的修正系数，结果表明这些计算式精确性比较高。WANG等[10-11]建立了循环净功的理论模型，推导理论计算公式，计算结果与ORC的数值计算结果也非常一致。HE等[12-13]建立了循环净功与优化蒸发温度的解析表达式，表明优化蒸发温度的理论值与ORC数值计算之间的偏差仅为–0.86%～2.3%，平均偏差小于1%。CHEN等[14]综述了ORC和超临界朗肯循环以及工质筛选标准，讨论了工质汽化潜热、密度、液态比热容对循环的影响和关于过热的经济性，推导出工质在膨胀机等熵膨胀过程中比焓变的关系式。另外，MAIZZA等[15]提出汽化潜热越大、密度越高、液态比热容越小的工质越适合于ORC，而YAMAMOTO等[16]认为低汽化潜热的工质更好，因为膨胀机进口处工质为饱和状态时才达到优化工况。LIU等[17]提出工质的饱和气线斜率公式，但未分析饱和气线斜率对循环性能的影响。

综上所述，常规有机朗肯循环一般是针对实际工质的数值计算、实验研究或应用，由于实际工质的种类有限，且工质物性是定量、非变量，使得有机朗肯循环的研究结果或结论往往是具体、局限的，不具有普遍性。基于前期研究提出的模拟有机朗肯循环的梯形循环及其理论模型[18]，本文建立工质饱和线形状（饱和液线斜率、饱和气线斜率与临界温度）及物性为自变量的数学关系，即将实际工质的物性变量化，应用梯形循环及其理论模型，进行梯形循环（或有机朗肯循环）的理论研究，从理论角度研究有机朗肯循环的普遍性热力学规律。重点针对有机朗肯循环中有极值功向无极值功转化的净功转折线，所对应的热源转折温度及其最高优化工况等特征进行研究。

1 工质饱和线的数学模型

前期研究提出并建立了梯形循环（trapezoidal cycle，TPC）及其理论模型[18]。梯形循环是将基本的内可逆ORC简化为T-s图中的梯形循环，如图1所示。其中将ORC中的两个过程作如下简化：①用过程3–4代替ORC中的过程3–3′–4，这样造成了液相区比功“Δw1”的减少（图中3–3′–4–3围成的面积）；②采用过程2′–2–2′代替ORC中干膨胀后的过热冷却过程2′–2′，这样，对于干工质或“干膨胀”，增加了比功“Δwsup.h”（图1中2′–2–2′–2′围成的面积），但对湿工质与等熵工质或“湿膨胀”，则无此功增量。计算表明[18]：TPC与ORC之间的偏差为：功率偏差为0.3%～–3.3%，热效率偏差为0.59%～–2.94%，相对偏差的绝对值均小于5%，表明梯形循环完全可以模拟有机朗肯循环。

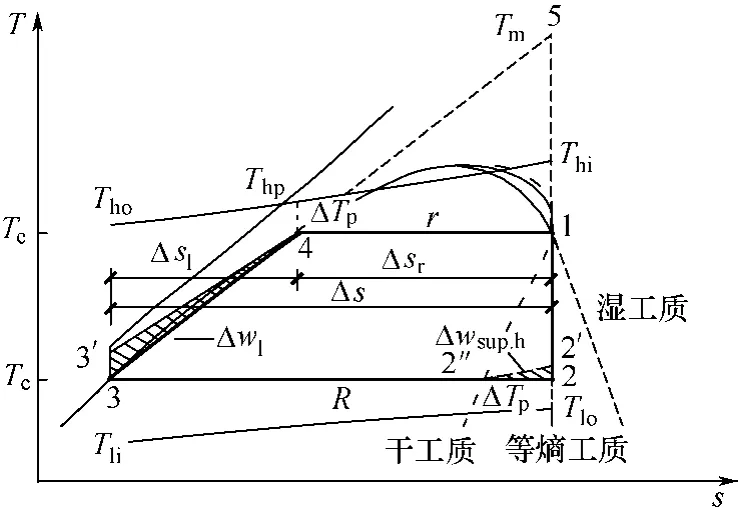
图1 有机朗肯循环与梯形循环

基于梯形循环及其理论模型，建立工质饱和线的数学模型。如图2(a)、(b)、(c)，线段4–5为工质饱和液线上蒸发温度处的切线，斜率为kl，线段1–5为工质饱和气线上蒸发温度处的切线，斜率为kg；并定义kl与kg之比为斜率比rk，rk=kl/kg。5点温度定义为斜率切线的交点温度Tcr'，其值可反映工质临界温度的高低。6点温度定义为顶点温度Tm。Tcr'与Tm之间的差值为ΔTm。

（1）对湿工质，如图2(a)，由三角形相似得式(1) 。

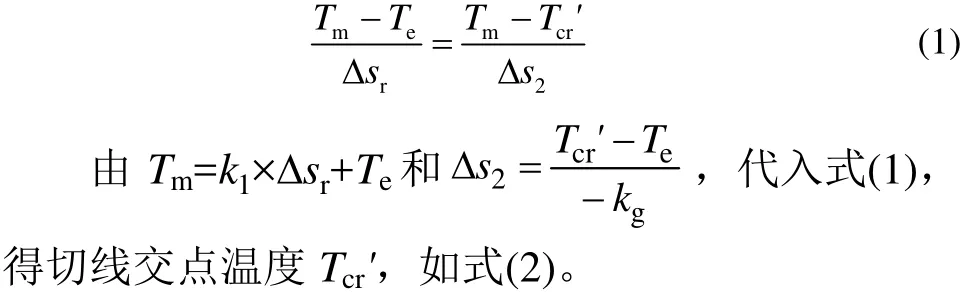
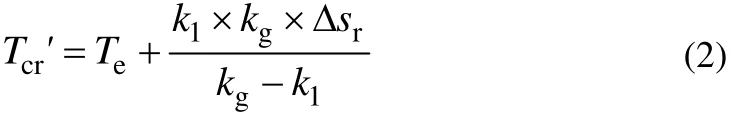
式中，Δsr为蒸发温度Te下两相区的熵变。

（2）对干工质，如图2(b)，由三角形相似得式(3)。

（3）对于等熵工质，Tcr'=Te+klΔsr，即公式(2)或公式(4)中kg→∞。

因此，干、湿及等熵工质的切线交点温度Tcr'表达式一致，公式(2)或公式(4)为通式。

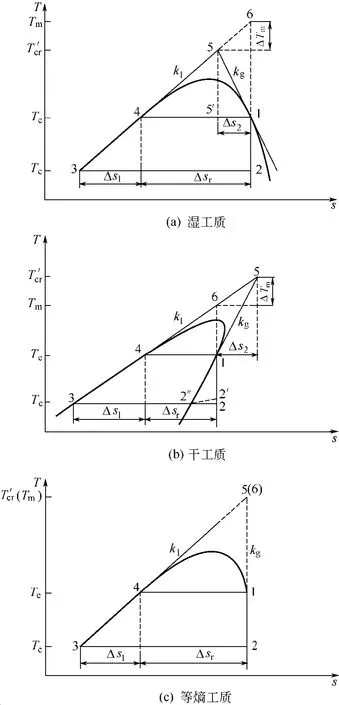
图2 顶点温度与饱和线斜率及斜率切线交点温度的关系

由此可推导出工质的顶点温度Tm表达式如式(5)。

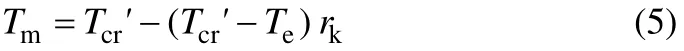
2 工质热源转折温度及其经验公式与偏差

研究表明：工质循环的优化工况（即净输出功极大值）只存在于蒸发器传热窄点位于工质泡点处的情况[18]。基于梯形模型，传热窄点位于工质泡点时的净输出功W表达式为式(6)。

如图3所示，热源转折温度Th,shift所对应的净功为有极值功向无极值功的转折；当热源温度低于该Th,shift时，工质循环存在优化工况，即存在净功极大值与对应的优化蒸发温度；当热源温度高于该Th,shift时，工质循环净功不再具有极大值，而是随蒸发温度单调上升。表明亚临界有机朗肯循环中存在着有极值功循环与无极值功循环，或功率由有极值向无极值的发展，如图4所示。明显地，热源转折温度下的优化工况为优化工况的最高工况，即热源转折温度Th,shift所对应的优化蒸发温度Te,opt_M与净输出功极值Wmax_M是优化工况的最高值。

研究表明，除净功的转折线与对应的工质热源转折温度，还存在另外两条净功特征线与对应的工质热源特征温度[19]，如图3所示：①热源转变点温度Th,turn，蒸发温度趋近于工质临界温度时，净功由一直下降出现向上增加趋势，对应的热源温度定义为热源转变点温度Th,turn；②热源上限温度Th,up，蒸发温度趋近于工质临界温度时，净功由一直上升出现下降趋势，对应的热源温度定义为热源上限温度Th,up。

表1给出了21种工质在蒸发器传热窄点温差5℃和冷凝温度35℃下，有机朗肯循环中工质热源转折温度，其中文献[19]的计算精确度为0.1℃，本文为0.01℃。表2给出了R227ea的热源转折温度随窄点温差（0～20℃）的变化。结果表明：①工质热源转折温度随蒸发器传热窄点温差成近似的线性关系；②热源转折温度所对应的最高优化工况：最高优化蒸发温度Te,opt_M与最大净输功极值Wmax_M不随蒸发器窄点温差而变化。

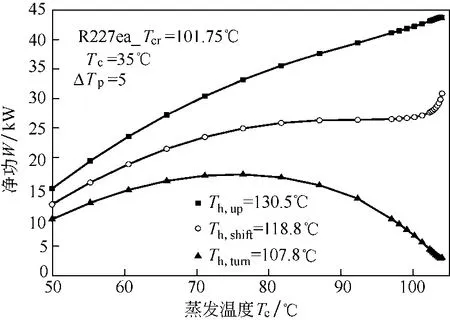
图3 工质R227ea循环净功特征线与对应的热源水特征温度

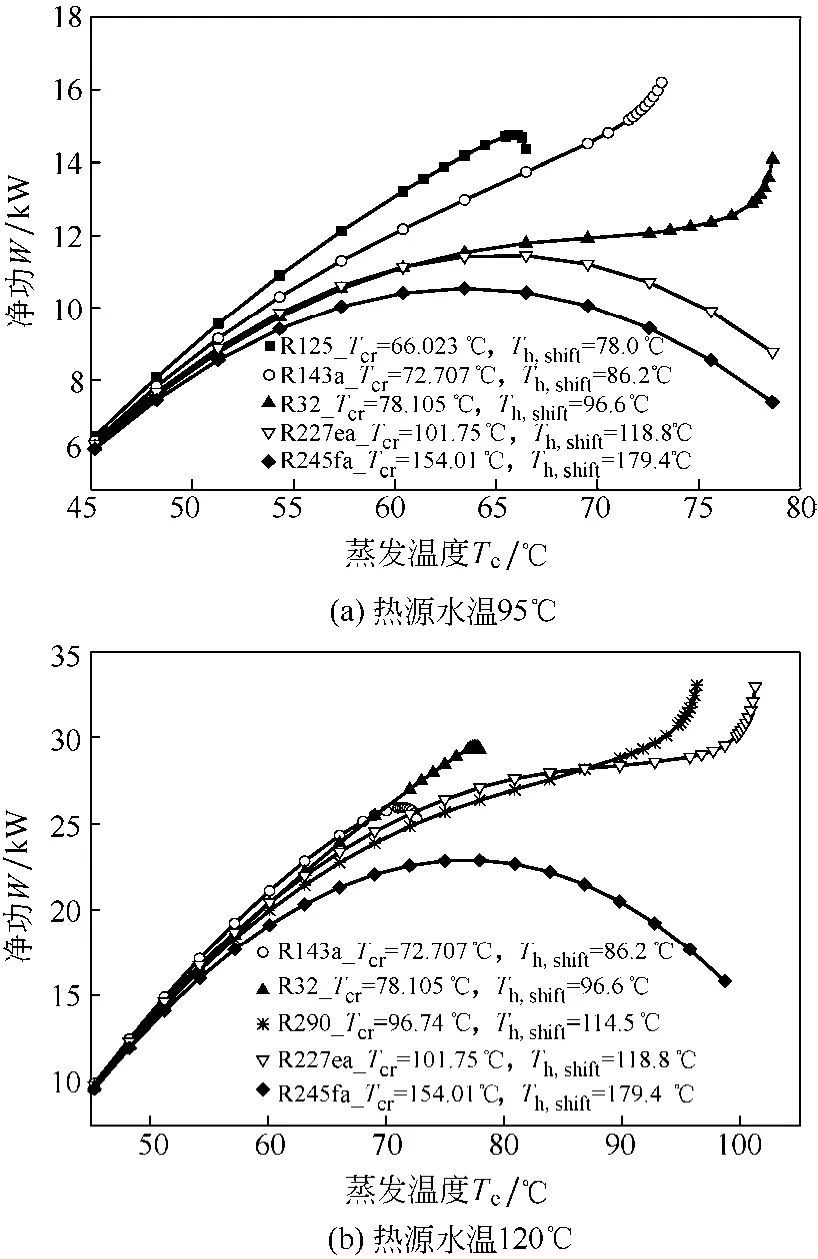
图4 一定热源水温度，不同临界温度工质的循环净功比较

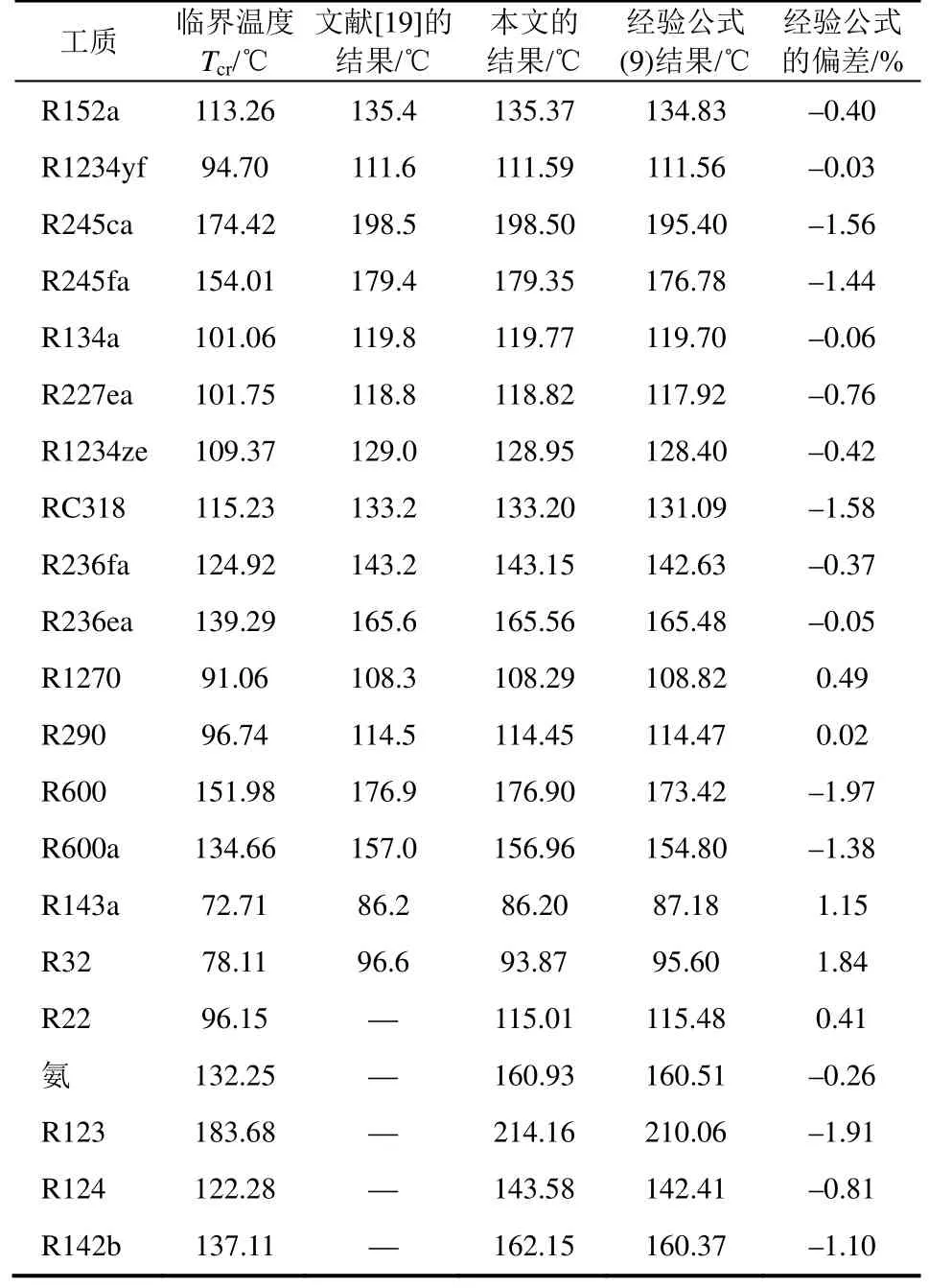
表1 工质的热源转折温度（ΔTp=5℃，Tc=35℃）

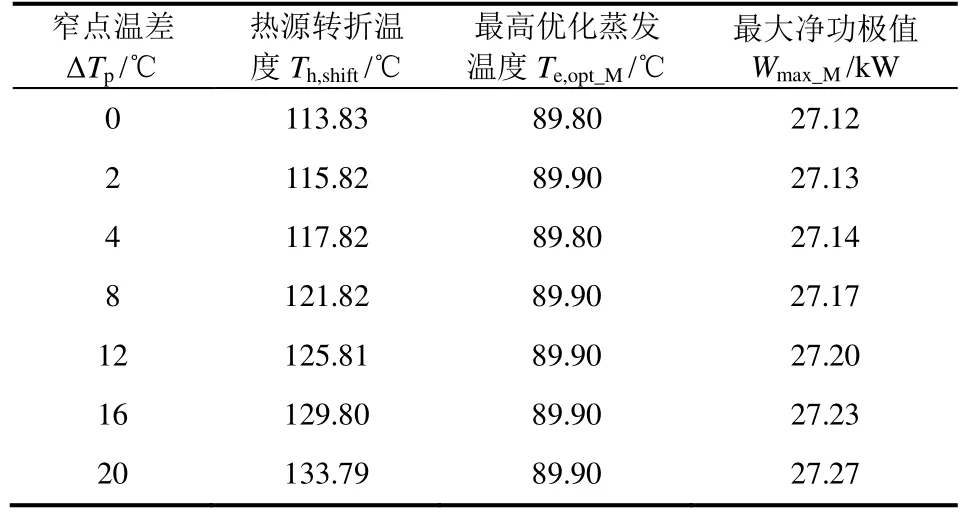
表2 R227ea在不同窄点温差下的热源转折温度及其最高优化工况值

通过对大量工质热源转折温度的计算与拟合，可推导出有机朗肯循环中工质热源转折温度的经验公式，如式(9)。

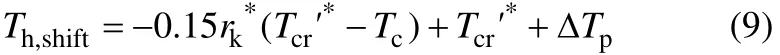
表1给出了热源转折温度经验公式与有机朗肯循环数值计算之间的偏差，二者的偏差较小，其中最大偏差为R600的1.97%。表明该经验公式可用于有机朗肯循环工质热源转折温度的模拟计算。

3 线性饱和线工质模型与热源转折温度及其理论公式

为简化分析，将工质的饱和液线与饱和气线简化为直线，构成线性饱和线工质，如图5。这样，线性饱和线工质的饱和液线斜率kl与饱和气线斜率kg不随温度而变化，为常量。

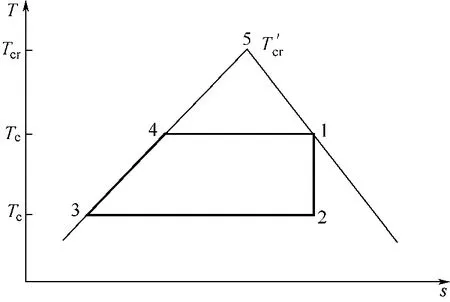
图5 线性饱和线工质模型

此时，线性饱和线工质的临界温度Tcr即为交点温度Tcr'。所以，公式(2)可写为式(10)。

蒸发温度处的潜热r=Te×Δsr，代入工质流量得到式(11)。

当蒸发温度Te达到顶点，即临界温度Tcr处，则为工质的热源转折温度（Th,shift_id），如式(14)。

式(14)表明：工质的热源转折温度与工质的临界温度及蒸发器窄点温差分别成线性关系，与前述的ORC分析结论相一致。

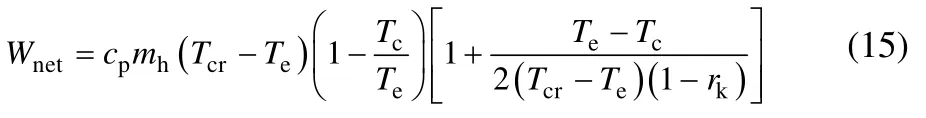
因此，由式(15)计算出的优化工况则为最高优化工况，即最高优化蒸发温度与最大净功极值。

但是由于mw并不是Te的一元函数，还是rk和cp的函数，所以式(14)会有偏差。取线性饱和线工质的临界温度Tcr范围90～200℃，斜率比rk为–2～0.35，对公式(14)的偏差进行计算如下。

当rk=0（即等熵工质）时，偏差范围为0～00.15℃，可以不用修正，仍采用式(14)。

当rk＞0（即干工质）时，偏差范围为0.15～– 0.05℃，可以不用修正，仍采用式(14)。

当rk＜0（即湿工质）时，修正为式(16)。

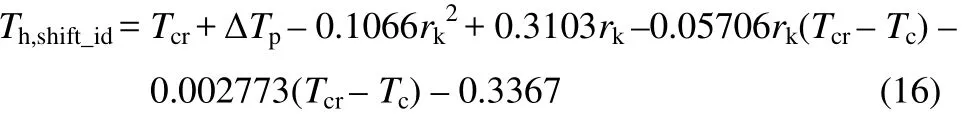
表3给出了临界温度Tcr150℃下，线性饱和线工质热源转折温度Th,shift_id的梯形循环数值计算与理论公式(14)或修正式(16)的计算结果。大量计算表明：在斜率比rk为–2～0.35范围内，线性饱和线工质热源转折温度的梯形循环数值计算与上述理论公式(14)或修正式(16)之间的最大偏差分别为：Tcr=100℃时为0.25%，Tcr=150℃时为0.24%，Tcr=200℃时为0.68%。

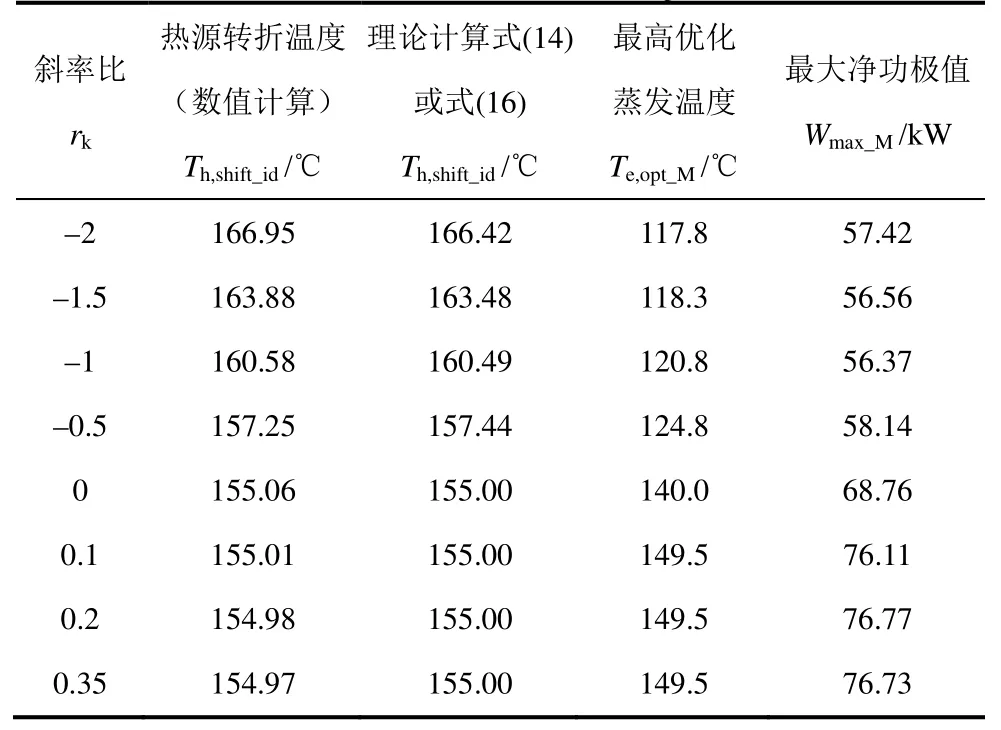
表3 线性饱和线工质热源转折温度下的优化工况与斜率比的关系（Tcr=150℃；ΔTp=5℃）

4 线性饱和线工质热源转折温度下的优化工况及其特征

由前述分析，工质热源转折温度Th,shifit_id下的优化工况为最高优化工况，即最高优化蒸发温度Te,opt_M与最大净功极值Wmax_M。

式(15)工质热源转折温度下净功计算式中无窄点温差 ΔTp，表明热源转折温度下的净功与窄点温差无关，由此可推论：热源转折温度下的最高优化工况参数（Te,opt_M、Wmax_M）也与窄点温差无关，与前述ORC的分析结论相一致。

下面具体计算与分析热源转折温度下的优化工况随斜率比的变化。假设计算条件为：热源水进口温度为工质热源转折温度Th,shifit_id，热源水流量mh为1kg/s，冷凝温度Tc为35℃，蒸发器窄点温差ΔTp为5℃；线性饱和线工质的临界温度Tcr设为150℃，斜率比rk为–2～0.35，计算结果见表3。表明最高优化工况随斜率比rk单调增加，至干工质时，最高优化工况达到工质的临界点。由于蒸发温度为Tcr时，热源进出口已无温差，可取比Tcr稍低的温度，如Tcr–0.5进行计算。

5 结论

有机朗肯循环中存在有极值功循环与无极值功循环，即存在一种净功的转折线与所对应的工质热源转折温度，它对工质的选择与循环性能评价具有指标性的作用。基于梯形循环及其理论模型，本文建立工质饱和线形状（饱和液线斜率、饱和气线斜率及其斜率比与临界温度）及物性为自变量的数学关系，并提出和定义了线性饱和线工质模型，建立循环性能与工质物性之间的数学关系。分别推导出有机朗肯循环中工质热源转折温度的经验公式，以及梯形循环中线性饱和线工质的热源转折温度理论公式及其修正。研究热源转折温度及其对应的优化工况的特征与一般性规律。得到如下结论。

（1）计算表明，21种工质热源转折温度的有机朗肯循环数值计算与经验公式之间的偏差小于1.97%。

（2）有机朗肯循环中，工质热源转折温度与蒸发器窄点温差成线性关系，热源转折温度所对应的最高优化工况（最高优化蒸发温度与最大净功极值）不随蒸发器窄点温差而变化。

（3）线性饱和线工质模型下，推导出工质热源转折温度Th,shift_id的理论公式，为临界温度与蒸发器窄点温差之和，其中湿工质要进行一定的修正。Th,shift_id下的最高优化工况（最高优化蒸发温度Te,opt_M与最大净功极值Wmax_M）随斜率比单调增加，至干工质时，最高优化工况接近工质的临界点。

符号说明

c—— 比热容，J/(kg·K)

Ja—— 雅克比数，J/J

k—— 斜率，K2·kg/J

m—— 质量流量，kg/s

q—— 比吸热量，J/kg

r—— 斜率比，kl/kg，量纲为1

s—— 比熵，J/(kg·K)

T—— 温度，K或℃

W—— 净输出功，J

w—— 比功，J/kg

η—— 热效率，%

上、下角标

c —— 冷凝

cr —— 临界

e —— 蒸发

h —— 热源

i —— 进口

m —— 顶点

max —— 极大值

opt —— 优化

ORC —— 有机朗肯循环

p —— 压力

shift —— 转折

TPC—— 梯形循环

w—— 工质

[1] 徐荣吉，张晓晖，闫美玉，等.过热/过冷对内回热有机朗肯循环影响的热力学分析[J].化工进展，2016，35（12）：3783-3792.XU Rongji，ZHANG Xiaohui，YAN Meiyu，et al.Thermal dynamics analysis on the organic Rankine cycle （ORC）with internal heat regenerator at superheated and subcooling conditions[J].Chemical Industry and Engineering Progress，2016，35（12）：3783-3792.

[2] 韩中合，潘歌，范伟，等.内回热器对低温有机朗肯循环热力性能的影响及工质选择[J].化工进展，2016，35（1）：40-47.HAN Zhonghe，PAN Ge，FAN Wei，et al.Effect of internal heat exchanger on thermodynamic performance of low temperature organic Rankine cycle and working fluid selection[J].Chemical Industry and Engineering Progress，2016，35（1）：40-47.

[3] 杨绪飞，戚风亮，刘秀龙，等.有机朗肯循环膨胀机入口过热度实验[J].化工进展，2016，35（7）：2007-2014.YANG Xufei，QI Fengliang，LIU Xiulong，et al.Experiment on expander inlet superheat of organic Rankine cycle[J].Chemical Industry and Engineering Progress，2016，35（7）：2007-2014.

[4] 王明涛，方筝，刘启一.涡轮增压柴油机余热利用的有机郎肯循环烃类高温工质热力学分析[J].化工进展，2016，35（9）：2721-2727.WANG Mingtao，FANG Zheng，LIU Qiyi.Thermodynamic analysis of an organic Rankine cycle for waste heat recovery of a turbo-charged diesel engine based on working fluids of alkanes[J].Chemical Industry and Engineering Progress，2016，35（9）：2721-2727.

[5] 张军辉，刘娟芳，陈清华.有机朗肯循环系统最佳蒸发温度和㶲分析[J].化工学报，2013，64（3）：820-826.ZHANG Junhui，LIU Fangjuan，CHEN Qinghua.Optimal evaporating temperature and exergy analysis for original Rankine cycle[J].CIESC Journal，2013，64（3）：820-826.

[6] 贺超，刘朝，高虹，等.工业余热有机朗肯循环参数优化和分析[J].工程热物理学报，2012，33（12）：2042-2046.HE Chao，LIU Chao，GAO Hong，et al.Parameters optimization and performance analysis of organic Rankine cycle for industrial waste heat recovery[J].Journal of Engineering Thermophysics，2012，33（12）：2042-2046.

[7] LI H，MA X L，WEI X L，et al.Selection of working fluids for low-temperature waste heat recovery using organic Rankine cycle[J].Advanced Materials Research，2012，512-515：1217-1222.

[8] YU H S，FENG X，WANG Y F.A new pinch based method for simultaneous selection of working fluid and operating conditions in an ORC （Organic Rankine Cycle） recovering waste heat[J].Energy，2015，90：36-46.

[9] 严家禄.低温热能发电方案中选择工质和确定参数的热力学原则和计算[J].工程热物理学报，1982，3（1）：1-7.YAN Jialu.Thermodynamic principles and formulas for choosing working fluids and parameters in desgning power plant of low temperature heat[J].Journal of Engineering Thermophysics，1982，3（1）：1-7.

[10] WANG D X，LING X，PENG H，et al.Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation[J].Energy，2013，50（1）：343-352.

[11] WANG D X，LING X，PENG H.Cost–effectiveness performance analysis of organic Rankine cycle for low grade heat utilization coupling with operation condition[J].Applied Thermal Engineering，2013，58（1-2）：571-584.

[12] HE C，LIU C，GAO H，et al.The optimal evaporation temperature and working fluids for subcritical organic Rankine cycle[J].Energy，2012，38（1）：136-143.

[13] HE C，LIU C，ZHOU M T，et al.A new selection principle of working fluids for subcritical organic Rankine cycle coupling with different heat sources[J].Energy，2014，68（15）：283-291.

[14] CHEN H，GOSWAMI D Y，STEFANAKOS E K.A review of thermodynamic cycles and working fluids for the conversion of low-grade heat[J].Renewable & Sustainable Energy Reviews，2010，14（9）：3059-3067.

[15] MAIZZA V，MAIZZA A.Working fluids in non-steady flows for waste energy recovery systems[J].Applied Thermal Engineering，1996，16：579-90.

[16] YAMAMOTO T，FURUHATA T，ARAI N，et al.Design and testing of the organic Rankine cycle[J].Energy，2001，26（3）：239-251.

[17] LIU B T，CHIEN K H，WANG C C.Effect of working fluids on organic Rankine cycle for waste heat recovery[J]. Energy，2004，29（8）：1207-1217.

[18] LI X G.A trapezoidal cycle with theoretical model based on organic Rankine cycle[J].International Journal of Energy Research，2016，40（12）：1624-1637.

[19] LI X G，ZHAO W J，LIN D D，et al.Working fluid selection based on critical temperature and water temperature in organic Rankine cycle[J].Science China Technological Sciences，2015，58（1）：138-146.

Shift-temperature of heating fluid and its characteristics for working fluid in organic Rankine cycle

LI Xinguo，WANG Wei，ZHAI Zhe，NAN Laifu，WANG Jingyi
（School of Mechanical Engineering，Tianjin University，Tianjin 300350，China）

The existence of the maximum power cycle and no maximum power cycle in organic Rankine cycle（ORC）means that there is a kind of shift-curve of net power output and its corresponding shift-temperature of heating fluid for the working fluids; which played an index function in the selection of the working fluids and the evaluation of the cycle performance. Based on trapezoidal cycle and its theoretical model，the relation and formulas of the saturated line shape（saturated liquid line slope，saturated gas line slope and its ratio and critical temperature）and thermal properties of the working fluids as variables were established. The model of working fluid with linear saturated line was proposed and defined. The mathematical model and relation between the cycle performance and properties of the working fluids were built. The empirical equations of the shift-temperature of heating fluid for the working fluid in ORC and the theoretical equations of the shift-temperature of heating fluid in working fluid with linear saturated line were derived，respectively. The characteristics and general principles of the shift-temperature of heating fluid and its corresponding optimum condition were investigated. Results showed that the deviation of shift-temperature of heating fluid with 21 working fluids between empirical equations and numerical simulations in ORC was less than 1.97%.The shift-temperature of heating fluid in model of working fluid with linear saturated line is the additionof the critical temperature of working fluid and the pinch point temperature difference of evaporator.The maximum optimal conditions（maximum optimal evaporation temperature and maximum net power output）corresponding to the shift-temperature of heating fluid increases with the ratio of the saturated line slope, which will be close to the critical point of the working fluid when it becomes the dry working fluid.

organic Rankine cycle；trapezoidal cycle；working fluid with linear saturated line；shift-temperature of heating fluid for working fluid；maximum optimum condition

TK123

：A

：1000-6613（2017）09-3223-08

10.16085/j.issn.1000-6613.2017-0056

2017-01-10；修改稿日期：2017-05-08。

国家自然科学基金项目（51276122）。

及联系人：李新国（1965—），男，博士，教授，主要从事工程热力学研究。E-mail：xgli@tju.edu.cn。