有关函数零点学习的误区与思考

霍建宇

(江苏省丰县中学高一(1)班，江苏 徐州 221700)

有关函数零点学习的误区与思考

霍建宇

(江苏省丰县中学高一(1)班，江苏 徐州 221700)

函数的零点是苏教版必修一函数章节中的重点内容，也是高中数学学习中的“老大难”问题.本文从零点认识的误区入手，进一步阐明零点的实质和求解方法，希望可以为其他同学的数学学习提供帮助.

高中数学；零点认识误区；函数零点

函数的零点是苏教版必修一函数章节中的一类重点题型，也是数学学习中的“老大难”问题.该内容在苏教版课本必修一中呈现如下知识点：

(1)零点含义

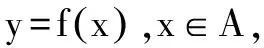
(2)零点的意义

(3)零点的存在性定理

事实上如果仅仅按照以上内容学习，学生就很难认识零点的实质，很难研究与此相关的问题.那么，针对零点的抽象学习该如何开展呢？笔者认为可从以下几个方面进一步阐明函数的零点问题.

误区一 零点是点

正解 0,2.

误区二 单调函数存在唯一零点

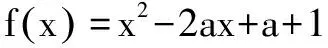
当函数在(0,1)上存在两个零点时，

由上可知所求a的取值范围为a<-1或a>2.

从上面几个有关零点的认识误区来看，学生真正的认清零点还有很大的空间．同时，从这里也可看出，不是教材内容本身有问题，而是自己没有认识零点的实质，没有正确使用零点的知识来解题．因此，在使用零点存在性定理来解决问题的时候，无需死守套路，完全可以根据其内容，深刻理解其内涵，计算与图形融为一体．

基于对零点的深刻认识，笔者认为在研究零点求解策略上有以下几点感悟：

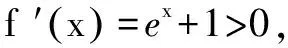
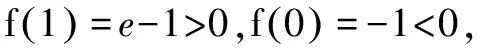
考虑两个临界位置：

有关零点的问题考查类型广泛，涉及到的数学思想方法众多，比如数形结合、函数与方程等等，在平时的学习中，我们要领会零点的实质，把握好解题策略，使我们不断远航.

[1]凤凰出版传媒集团，江苏教研室，苏教版高中数学教材编写组.数学必修(1-5)[M].南京：江苏凤凰教育出版社，2016.

[责任编辑：杨惠民]

2017-05-01

霍建宇(2001.09-)，江苏省丰县人，现为江苏省丰县中学高一(1)班学生.

G632

B

1008-0333(2017)19-0054-02