导数的应用错例解析

王乾兵

(山东临沂临港经济开发区临港一中，山东 临沂 276624 )

导数的应用错例解析

王乾兵

(山东临沂临港经济开发区临港一中，山东 临沂 276624 )

导数作为一种工具，在解决数学问题时极为方便，但是笔者在教学过程中，发现导数的应用还存在许多误区.

导数，求最值，求单调区间，单调性.

一、导数的定义理解不清

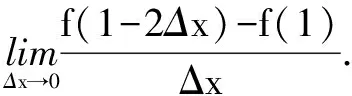
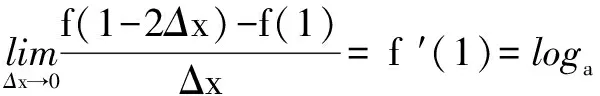
二、f ′(x0)为极值的充要条件理解不清

例2 函数f(x)=x3+ax2+bx+a2在x=1处有极值10，求a、b的值.

错解f′(x)=3x2+2ax+b,由题意知f′(1)=0,且f(1)=10,即2a+b+3=0,且a2+a+b+1=10,解之得a=4,b=-11 ,或a=-3,b=3.

剖析 错误的主要原因是把f′(x0)为极值的必要条件当作了充要条件，f′(x0)为极值的充要条件是f′(x0)=0且x0附近两侧的符号相反.所以后面应该加上：当a=4,b=-11时f′(x)=3x2+8x-11=(3x+11)(x-1),在x=1附近两侧的符号相反，∴a=4,b=-11.

当a=-3b=3时f′(x)=3(x-1)2, 在x=1附近两侧的符号相同，所以a=-3,b=3舍去.(a=4,b=-11时，f(x)=x3+4x2-11x+16的图象见下面左图;a=-3,b=3时f(x)=x3-3x2+3x+9的图象见下面右图)

三、函数的单调区间不完善

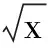
剖析 错解错在对函数在x=1处是否连续没有研究，显然函数在x=1处是连续的，所以函数的单调递增区间是(0，+∞).对于f′(x) >0(或f′(x) <0)的解集中的断开点的连续性，我们要进行研究，不能草率下结论.

四、函数单调的充要条件理解不清

五、求函数的最值没有考虑函数的不可导点

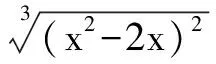
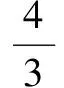
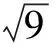
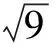
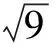
六、求函数的极值没有考虑函数的不可导点

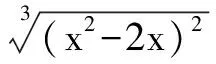
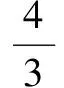
当x=1时，f′(x) 在x=1附近两侧的符号相反，左正右负，∴x=1是函数的极大值点

剖析 错误的主要原因是解题过程中忽略了对函数的不可导点的考察，因为函数的极值可以在定义域内导数为零的点或不可导点取得.所以后面还应该加上：在定义域内不可导的点为：x1=0,x2=2 ，经计算，f′(x)在x1=0附近两侧的符号相反，左负右正，f′(x)在x2=2附近两侧的符号相反，左负右正， ∴x1=0和x2=2是函数的两个极小值点.∴函数的极大值为f(1)=1,极小值为f(0)=f(2)=0.(函数的图象见上图)

[1]人民教育出版社，课程教材研究所，中学数学课程教材研究开发中学.普通高中课程标准实验教科书(数学必修5)[M].北京：人民教育出版社，2008.

[责任编辑：杨惠民]

2017-05-01

王乾兵，男，山东日照人，中学一级数学教师，曲阜师范大学本科毕业，主要研究方向是中学数学及应试能力.

G632

B

1008-0333(2017)19-0030-02