浅谈教学中创造性思维的培养

王建春

(江苏省邳州市八义集高级中学，江苏 徐州 221361)

浅谈教学中创造性思维的培养

王建春

(江苏省邳州市八义集高级中学，江苏 徐州 221361)

在新课程的教育理念下，培养学生积极主动、勇于探索的学习能力已经成为一个重要课题，如何培养学生的创造性思维成为关键.创造性的思维必须有创新意识和创新精神做支撑，这就要求广大教师在新理念的指导下创新教学模式，改革教学方式，提升教学质量，还原教育本质，提升学生的学科核心素养.

创造性思维；独立性； 综合性

一、主动发展 培养独立性思维

素质教育的工作重点就是要培养受教育者的创新精神和实践能力.所以在教学实践中，要面向全体学生，“让学生主动发展”，有意识地鼓励学生养成独立思维的意识和习惯，敢于发表独立见解，并付诸实践.

比如《必修2》32页有这样一个例题：

例1 已知：a∥b,a⊥α，求证：b⊥α．

这道题目教材是通过定义法证明b垂直与平面α内的任意一条直线，我在课堂讲解这道例题时，除了课本上的方法外，积极引导学生思考其他证明方法.现把学生的一种证法整理如下：

证明：在平面α内作两条相交直线m,n且m∩n=A.

∵直线a⊥α，

∴a⊥m,a⊥n(直线与平面垂直的定义知).

又∵a∥b，∴b⊥m，b⊥n．

又∵m⊂α，n⊂α，m∩n=A,∴b⊥α.

再比如在学习“§1.2.1平面的基本性质”中的公理2“如果两个平面有一个公共点，那么它们还有其他公共点，这些公共点的集合是经过这个公共点的一条直线”时，我随手拿起两本书作为平面模型让学生体会两个平面的公共点，我故意将其中一本书的端点与另一本书的表面接触，让学生感受到发散思维：两个平面会不会只有一个公共点？这时候学生分组开始讨论.我再利用两张纸演示“平面的无限延伸性”，其中一张纸带有缝隙，再次演示一个交点的情况，顺势将一张纸插到另一张的缝隙中，这会让学生有深刻的印象，培养学生创造性思维.

二、全面发展，培养综合性思维

数学课堂中，要积极培养学生的综合性思维，只有在在教学实践中积极运用综合思维，才能提高学生的综合能力和学科素养.

比如这样一道题：如果二次函数y=mx2+(m-3)x+1图象与x轴的交点至少有一个在原点的右侧，试求m的取值范围.

分析 这道题要是直接求解需要从三个方面讨论，这样非常冗繁，此时可以引导学生进行逆向思维，从反面思考，考虑函数图象与x轴的交点均在原点的左侧可得m≥9，其反面m<9，再考虑Δ≥0,m≠0，可得m的取值范围是m≤1且m≠0(解略).

2.思维的“类比推理”.思维也像数学的“类比推理”一样：寻求事物之间的关系，类比从特殊到特殊.

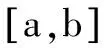
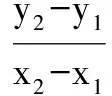
三、创造想象，培养跳跃性思维

爱因斯坦指出：“想象力比知识更重要，因为知识是有限的，而想象力概括着世界上的一切，严格地说，想象力是科学研究中的实在因素.”教师要在民主、平等、轻松的教学情境中，实现创造性的学习活动，并有针对性地进行跳跃性思维的训练.

例如：在正四棱锥O-ABCD中，E、F分别为AD，BC中点，且OE⊥OB,P为平面OEF与此正四棱锥内切单位球球面的交线上一动点，求P点到三角形OEF三个顶点距离平方和的最大值与最小值.

分析 此题分两步考虑.第一步是确定△OEF的形状，第二步是对△OEF内切单位圆上动点求“距离”的最大值与最小值.

猜测：根据经验及题目条件，凭直觉将会预感到这个△OEF是一个等腰直角三角形.通过证明，易得△OEF是等腰直角三角形.之后只要以O为原点，OE、OF为坐标轴建立直角坐标系，问题即趋于明朗化.

教学中，教师把课堂还给学生，相信学生，让学生“先发制人”，大胆直觉、猜想，思维“完美跳跃”，这才是走向成功的捷径.

四、一题多解，培养发散性思维

散性思维是创造性的思维，要求思维朝着各个方向发散开去，达到流畅、变通、独特.

比如：正三角形两个顶点的坐标是A(1,0),B(2,1),第三个顶点C在第一象限，求C点坐标.

此题比较简单，但如果能就此例组织一题多解教学，那么，对培养发散性思维能力，将会收益匪浅.

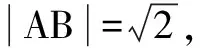
解法4 (参数法)(理)

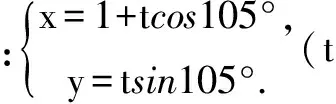
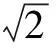
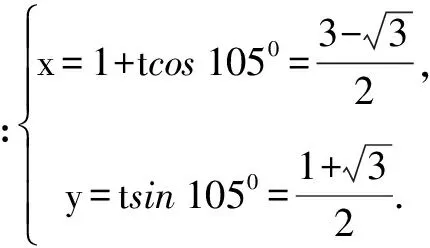
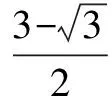
解法5 (极坐标法)(理)

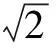
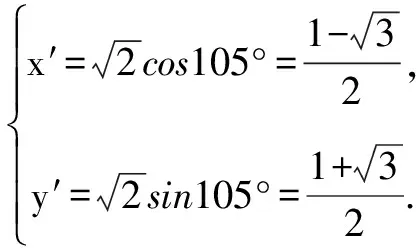
在平时教学中，教师应帮助学生树立数学精神，求真精神、创新精神，领悟数学的真谛，也许这才是学生受益一生的东西.

[1]李孝成.中学数学教学中培养学生创造性思维能力[J].数学教学通讯，2012(24).

[2]李志.物理教学中对学生创造性思维的培养[J].数理化解题研究，2016(36).

[责任编辑：杨惠民]

2017-06-01

王建春(1983.05-)，男，黑龙江省伊春人，中学一级，本科学历，从事数学课堂的兴趣培养.

G632

B

1008-0333(2017)19-0025-02